1 Introduction
The mass or binding energy is one of the fundamental physical quantities of a nucleus, reflecting the intricate interplay of nuclear forces that hold the protons and neutrons comprising the nucleus together [1]. It is pivotal not only in determining nuclear stability [2] but also in governing phenomena ranging from energy productions in stars [3] to the synthesis of elements in the universe [4]. Hence, understanding the nuclear mass is crucial to nuclear physics [5] and has profound implications across various scientific disciplines including astrophysics [6,7,8]. Precision measurements and reliable predictions of nuclear masses enable advancements in the comprehension of nuclear structure, inform astrophysical models, and drive innovations in energy production through nuclear fusion and fission.
Experimentally, over 3300 nuclides have been produced and identified [9,10,11]. The global construction and upgrading of facilities for rare isotope beams such as the HIAF (High Intensity heavy-ion Accelerator Facility at Huizhou) [12] and HIRFL (Heavy Ion Research Facility in Lanzhou) [13] in China, the FRIB (Facility for Rare Isotope Beams) in America [14], the RIBF (Radioactive Isotope Beam Factory at RIKEN) in Japan [15], the FAIR (Facility for Antiproton and Ion Research) in Germany [16], the RAON (Rare isotope Accelerator complex for ON-line experiments) in Korea [17], the SPIRAL2 (Système de Production d’Ions Radioactifs Accélérés en Ligne de 2e génération) in France [18], and the ISAC (Isotope Separator and Accelerator) in Canada [18] have been greatly advancing research in nuclear physics. As for the study of nuclear masses, the masses of approximately 2500 nuclides among the discovered ones have been measured [19,20,21]. Nonetheless, the existence of more than 7000 nuclides has been predicted [22], yet those with known masses remain somewhat distant from the path of the r-process [23], a crucial pathway for producing elements heavier than iron in the universe. Even in the foreseeable future, most of the unknown neutron-rich nuclei will remain beyond experimental capabilities. For instance, the determination of the neutron dripline that depicts the neutron-rich boundary of the nuclear landscape has only recently reached the isotopic chain of neon with 10 protons [24, 25]. Therefore, reliable predictions of nuclear masses are urgently desired.
Significant efforts have been dedicated to describing measured nuclear masses and predicting unknown ones. In this field, one may distinguish two main classes of theoretical approaches. The first, referred to as local or regional theories, relies on specific assumptions that correlate the masses of nuclei within a defined set, such as neighbors or mirror pairs. Examples include the Garvey-Kelson local mass relation [26, 27], the nucleon interaction model [28, 29], the Audi-Wapstra extrapolation method [30, 31], the isobaric multiplet mass equation [32, 33], and mass relations of mirror nuclei [34, 35]. These approaches often achieve remarkably high accuracy for target nuclei located within 3 to 5 steps of the boundary of known data in the nuclear chart [36].
The second class is the so-called global theories, which can be further subdivided into two categories: the macroscopic-microscopic mass model and the microscopic density functional theory (DFT). While macroscopic-microscopic models like the finite-range droplet model (FRDM) [37] and the Weizsäcker-Skyrme (WS) model [38] have achieved high accuracy in describing known nuclear masses, DFT is generally considered to have more reliable predictive power. A detailed discussion in this regard will follow in Section 2. Microscopic DFT provides a robust framework for consistently describing nearly all nuclides across the nuclear landscape [39,40,41,42,43,44,45,46,47,48,49,50]. The covariant density functional theory (CDFT) [51], a relativistic extension of DFT, has proven highly effective in describing a wide range of nuclear phenomena in both ground and excited states [51,52,53,54,55,56,57,58,59,60]. The success of CDFT is attributed to its inherent advantages, including the automatic incorporation of spin-orbit interaction [61], a natural explanation for pseudospin symmetry in the nucleon spectrum [62,63,64] and spin symmetry in the antinucleon spectrum [64,65,66], as well as the self-consistent treatment of nuclear magnetism [67, 68].
Within the framework of CDFT, the relativistic continuum Hartree-Bogoliubov (RCHB) theory was developed by solving the relativistic Hartree-Bogoliubov (RHB) equation in coordinate space [69, 70]. In such a way, the RCHB theory self-consistently incorporates both pairing correlations and continuum effects, enabling it to describe nuclei across the entire nuclear landscape, from the stability valley to the dripline [54]. The RCHB theory has provided a microscopic interpretation of the neutron halo in the first discovered halo nucleus, 11Li [69], and has predicted the giant halo phenomena [71, 72], neutron halos in hypernuclei [73], and new magic numbers in superheavy nuclei [74]. The integration of the RCHB theory with nuclear reaction models has successfully reproduced the charge-changing cross sections [75] and elastic proton-nucleus scattering cross sections [76] in a wide range. Notably, the first relativistic nuclear mass table that includes continuum effects has been constructed with the RCHB theory, predicting the existence of 9035 bound nuclei with proton numbers \(8\le Z\le 120\), significantly extending the neutron-rich boundary of the nuclear chart well beyond previous theoretical predictions [77]. Based on the RCHB mass table, global studies of \(\alpha\) decay [78] and proton radioactivity [79] have been conducted. However, the accuracy of the RCHB mass table in describing existing mass data is limited by the assumption of spherical symmetry.
Most nuclei in the nuclear chart, except for doubly-magic ones, deviate from spherical shape. To consider the deformation and continuum effects simultaneously, one could, in principle, solve the deformed RHB equation in coordinate space. Nonetheless, this proves extremely challenging, if not practically infeasible [80]. As an alternative, the solution in a Woods-Saxon basis was proposed, which has been shown to yield results consistent with those obtained in coordinate space [81]. By solving the deformed RHB equation in a Dirac Woods-Saxon (DWS) basis [81], the deformed relativistic Hartree-Bogoliubov theory in continuum (DRHBc) was developed [82,83,84,85], in which the axial deformation degrees of freedom, pairing correlations, and continuum effects are taken into account in a microscopic and self-consistent manner. The applications of the DRHBc theory span a variety of nuclear phenomena, with particular success demonstrated [57, 86,87,88,89,90,91] in the description of halo nuclei and candidates such as 17B [92], 19B [93], 15,19,22C [94,95,96], 31Ne [97, 98], and 37Mg [99, 100], as well as the prediction of deformed halos in 39Na [101] and 42,44Mg [82, 83]. Given its success, it is a natural progression to construct a nuclear mass table that incorporates both deformation and continuum effects based on the DRHBc theory. The DRHBc mass table project has been ongoing for several years, making remarkable progress in this endeavor.
In this review, we focus on the recent advancements in the construction of the DRHBc mass table and its relevant applications. In Section 2, we present the predictive power and accuracy of the DRHBc mass table, highlighting important achievements made during its development. In Section 3, we introduce the refinement of the RCHB mass table using machine learning, discussing how the encoded physical effects and extrapolation reliability are examined using the DRHBc mass table. Finally, we provide a summary and outline potential directions for future improvements to the DRHBc mass table in Section 4.
2 The DRHBc mass table
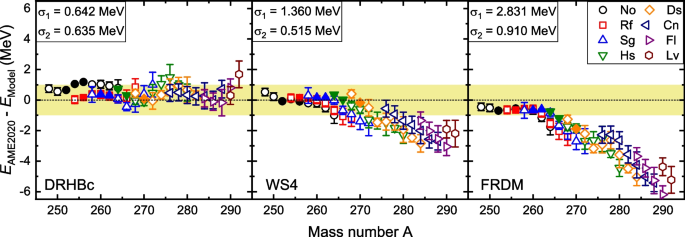
The DRHBc theory inherits the advantages of the RCHB theory while incorporating the deformation effect. Its predictive power on nuclear masses has been examined by taking even-even nuclei with \(Z \geqslant 102\) as examples. Figure 1 exhibits the mass differences between the DRHBc results [102] and available data from the latest “Atomic Mass Evaluation"(AME2020) [21], including 10 measured data for 252,254,256No, 256,258Rf, 260,262Sg, 264,266Hs, and 270Ds, as well as 46 empirical data. Results for the popular macroscopic-microscopic mass models WS4 [38] and FRDM(2012) [37] are also shown for comparison. The root-mean-square (rms) deviation for the 10 measured masses in DRHBc is 0.635 MeV, on the same level as 0.515 MeV by WS4 and 0.910 MeV by FRDM. After including the 46 empirical data, the rms deviation in DRHBc slightly changes to 0.642 MeV, while that increases markedly to 1.360 MeV in WS4 and 2.831 MeV in FRDM. The empirical data in AME2020 are derived by integrating the trends of the mass surface with the available experimental information [21], and their precision is often validated by later experiments [103, 104]. Figure 1 demonstrates that the DRHBc theory describes well the isospin dependence of nuclear masses along both the isotopic and isotonic chains. These results stand in significant contrast to macroscopic-microscopic models, clearly showcasing the predictive power of the DRHBc theory. Recently, the reliable predictive power of the DRHBc theory has been further validated in the superheavy nuclear region with odd-mass and odd-odd nuclei included. The corresponding results can be found in Fig. 1 of Ref. [105], and the discussion here is still qualitatively valid.
Mass difference between the AME2020 data [21] and a the DRHBc calculation, b the WS4 mass model [38], and c the FRDM(2012) mass model [37] for superheavy even-even nuclei with data available (\(102\le Z\le 116\)), including 10 measured data for 252,254,256No, 256,258Rf, 260,262Sg, 264,266Hs, and 270Ds, as well as 46 empirical data. \(\sigma _1\) (\(\sigma _2\)) represents the root-mean-square deviation from the available 56 (10) measured and empirical (measured only) masses denoted by solid and open (solid) symbols. Taken from Ref. [102]
Given the achievement of the RCHB mass table and the predictive power of the DRHBc theory, it is desirable to construct, using the DRHBc theory, an upgraded microscopic nuclear mass table that simultaneously incorporates the deformation and continuum effects. While such a mass table would be computationally much more expensive than the RCHB one, a DRHBc Mass Table Collaboration consisting of more than 30 research teams has been organized [106, 107]. The DRHBc theory has been extended to a version with point-coupling density functionals, and systematic numerical convergence checks from light to heavy nuclei for the DRHBc calculations have been performed to confirm the numerical details for large-scale, global calculations [108, 109]. To efficiently determine ground states for odd nuclei, an automatic blocking procedure has been implemented and justified in the point-coupling DRHBc theory [110].
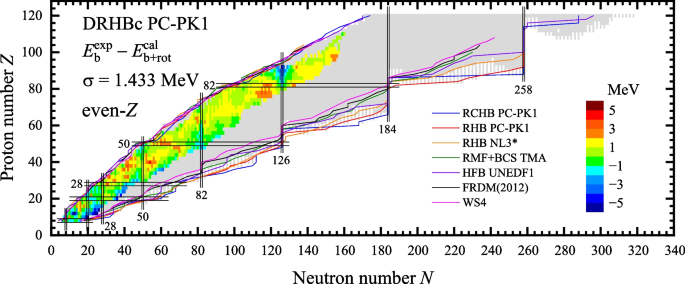
So far, systematic DRHBc calculations for even-Z nuclei with \(8 \leqslant Z \leqslant 120\) have been performed with the PC-PK1 [111] density functional, and the ground-state properties including binding energies, separation energies, rms radii, quadrupole deformation, etc. have been compiled in Refs. [112, 113]. Figure 2 presents the nuclear landscape of even-Z nuclei with \(8 \leqslant Z \leqslant 120\) explored by the DRHBc theory. In total 4829 even-Z nuclei are predicted to be bound, including 2584 even-N and 2245 odd-N nuclei. Among them, the masses of 1244 nuclei (including 634 even-even and 610 even-odd ones) have been experimentally available [21]. The mass differences between the data and the DRHBc predictions are scaled by colors in Fig. 2. It can be found that the results from the DRHBc theory are in satisfactory agreement with the experimental data. The accuracy of the present DRHBc mass table for even-Z nuclei is 1.433 MeV, representing one of the best density-functional descriptions for nuclear masses.
4829 bound even-Z nuclei from O (\(Z = 8\)) to \(Z = 120\) predicted by the DRHBc theory with PC-PK1. For the 1244 even-Z nuclei with mass measured, the binding energy differences between the data [21] and the DRHBc calculations (with rotational correction energy included) are scaled by colors. The nucleon driplines predicted by different mass tables, including RCHB with PC-PK1 [77], RHB with PC-PK1 [50] and with NL3* [46], RMF+BCS with TMA [41], HFB with UNEDF1 [22], FRDM(2012) [37], and WS4 [38], are plotted for comparison. Taken from Ref. [112]
Table 1 lists the rms deviations of the DRHBc predicted binding energies, two-neutron separation energies, one-neutron separation energies, and two-proton separation energies with respect to the available data, together with those of other density functional calculations for a quantitative comparison. The data number in Table 1 represents the number of overlaps between the bound nuclei in the theoretical model and the experimentally bound nuclei with available measured data in AME2020 [21]. Compared with other results, the present DRHBc calculations provide the most accurate description for nuclear masses when including rotational correction energies, which have proven to induce a remarkable refinement for the density-functional calculations based on PC-PK1 [49]. The comparison with the RCHB mass table highlights the significance of incorporating deformation effects in the description of nuclear masses.
Table 1 The rms deviations for the binding energies, two-neutron separation energies, one-neutron separation energies, and two-proton separation energies in the DRHBc calculations with PC-PK1 with respect to the AME2020 data [21] in the unit of MeV.
| Model | Density functional | \(\boldsymbol{\sigma }(\boldsymbol{E}_{\textbf{b}})\) | \(\boldsymbol{\sigma (S}_{\textbf{2n}}\boldsymbol{)}\) | \(\boldsymbol{\sigma (S}_{\textbf{n}}\boldsymbol{)}\) | \(\boldsymbol{\sigma (S}_{\textbf{2p}}\boldsymbol{)}\) | Data number | Reference |
|---|---|---|---|---|---|---|---|
| DRHBc\(^{\mathrm {w/o}\ E_{\textrm{rot}}}\) | PC-PK1 | 2.562 | 0.953 | 0.749 | 0.929 | 1244 | [112] |
| DRHBc\(^{\mathrm {w/} \ \ E_{\textrm{rot}}}\) | PC-PK1 | 1.433 | 0.989 | 0.774 | 1.046 | 1244 | [112] |
| RCHB | PC-PK1 | 8.082 | 1.492 | 0.835 | 1.561 | 1232 | [77] |
| RMF+BCS | TMA | 2.063 | 0.897 | 0.730 | 1.114 | 1249 | [41] |
| HFB | SkM* | 7.248 | 1.134 | 0.693 | 1.781 | 1239 | [22] |
| HFB | SLy4 | 5.275 | 0.914 | 0.598 | 0.855 | 1249 | [22] |
| HFB | SV-min | 3.391 | 0.731 | 0.481 | 0.778 | 1248 | [22] |
| HFB | UNEDF1 | 1.934 | 0.692 | 0.520 | 0.780 | 1250 | [22] |
Separation energies derived from nuclear masses are important ground-state properties that reflect nuclear stability and determine the boundary of the nuclear landscape. As listed in Table 1, the accuracies for both two-neutron and two-proton separation energies are around 1 MeV by most density-functional descriptions, and that for the one-neutron separation energy ranges from about 0.5 to 1.0 MeV. It is also noted that the rotational correction does not improve the description of separation energies in the DRHBc results, as the adopted cranking approximation is not suitable for spherical and weakly deformed nuclei [108]. To solve this problem, the two-dimensional collective Hamiltonian (2DCH) method based on the DRHBc theory has been developed [114], which is proved capable of improving the description of both nuclear masses and separation energies for even-even Nd, Kr, and Sr isotopes [114, 115].
In Fig. 2, the neutron and proton driplines predicted in the DRHBc mass table, together with those predicted by several other mass-table-type calculations [22, 37, 38, 41, 46, 50, 77], have been plotted. The proton driplines predicted by different models are quite similar to each other and roughly consistent with experimental observations. This is mainly because the continuum effects on the proton dripline are effectively suppressed by the existence of the Coulomb barrier. However, the predicted neutron driplines obviously differ by model. Several factors may affect the location of the neutron dripline, e.g., the treatment of continuum effects, the adopted density functional and pairing interaction, and the deformation degrees of freedom under consideration [113]. The DRHBc mass table in general presents a more extended neutron dripline, largely due to the proper incorporation of continuum effects and the robust description of the isospin dependence of nuclear masses by PC-PK1. Interestingly, in the DRHBc nuclear landscape some nuclei are predicted to be bound beyond the primary neutron dripline in the regions of \(50 \leqslant Z \leqslant 70\) [116], \(80 \leqslant Z \leqslant 90\), and \(100 \leqslant Z \leqslant 120\) [102, 105, 117], forming peninsulas of stability adjacent to the nuclear mainland. It is found that deformation plays an indispensable role in the formation of such stability, while pairing correlations, continuum effects, and odd-even effects also contribute in a self-consistent way.
During the construction process of the even-Z part, the DRHBc Mass Table Collaboration has achieved a series of remarkable successes. A variety of nuclear phenomena have been successfully interpreted with the DRHBc theory:
-
The halo structures in 17B [92], 19B [93], 15,19,22C [94,95,96], 31Ne [97, 98], and 37Mg [99, 100].
-
The neutron skin thickness in Pb isotopes [118].
-
The prolate shape dominance in Te, Xe, and Ba isotopes [119].
-
The odd-even shape staggering and the kink structure in the evolution of charge radii in Hg isotopes [120].
-
The one-proton emissions in 148–151Lu [121].
-
The \(\alpha\)-decay half-lives of the even-even nuclei from W to U [122], and those of the Tl, Bi, and At Isotopes [123].
-
Nuclear shape evolution in neutron-deficient Au and the kink structure in the evolution of charge radii in Pb isotopes [124].
Theoretical investigations on possible novel structures or mechanisms have been conducted with the DRHBc theory:
-
Possible deformed neutron halos in 39Na [101] and 42,44Mg [82, 83].
-
Nucleons in the classically forbidden region for magnesium isotopes [125].
-
Possible peninsulas of stability beyond the primary neutron dripline [102, 105, 116, 117].
-
Possible shape coexistence and bubble structures from Lu to Hg isotopes [128, 129] and from F to K isotopes [130].
-
The evolution of \(N = 20\), 28, and 50 shell closures in the \(20 \leqslant Z \leqslant 30\) region [131].
-
The shell structure and shape transition in superheavy nuclei with \(Z=117\) and 119 [132].
-
The symmetry energy from two-nucleon separation energies for Ca and Pb isotopes [133].
-
The inner fission barriers in even-even uranium isotopes from the proton to the neutron dripline [134].
-
Possible superheavy magic numbers [135,136,137] and the influence of high-angular-momentum single-particle states [138] in superheavy nuclei.
-
The evolution of shell structure in U, Pu, and Cm isotopes [139].
-
The ground-state properties and structure evolutions of odd-A transuranium Bk isotopes [140].
-
Systematics of the charge radii for even-Z nuclei and their deformation correlation [141].
Several extensions and optimizations of the DRHBc theory have also been achieved:
-
Implementation of the angular momentum projection to explore the rotational excitations of exotic nuclei [86, 142, 143].
-
Implementation of the finite amplitude method to study the isoscalar giant monopole resonance in exotic nuclei [144].
-
Implementation of the 2DCH to study the beyond-mean-field dynamical correlations and improve the description for ground-state properties [114, 115].
-
Combination with the Glauber model to study nuclear reaction observables [91, 96, 97, 100, 145, 146].
-
Optimization of the DWS basis for large-scale DRHBc calculations [147].
-
Development of the triaxial relativistic Hartree-Bogoliubov theory in continuum (TRHBc) that further includes triaxility [87, 148,149,150,151].
-
Development of the time-odd DRHBc (TODRHBc) theory that strictly treats nuclear magnetism [89, 98].
-
Combination with the Lipkin-Nogami method to investigate the possible giant halo in 66Ca [152].
-
Astrophysical r-process simulation based on a “pseudo” DRHBc mass table and the exploration of deformation effects on the r-process path [153].
Systematic DRHBc calculations for odd-Z nuclei with \(8 \leqslant Z \leqslant 120\), as well as the superheavy nuclei with \(121 \leqslant Z \leqslant 136\), are in progress to complete the DRHBc mass table. It is worth anticipating more fascinating applications and significant advancements of the DRHBc theory through the collaborative efforts.
3 Machine learning nuclear masses
To accurately describe nuclear masses, one must, in principle, account for all the underlying effects of nuclear quantum many-body systems, including bulk effects, deformation effects, shell effects, odd-even effects, and potentially unknown ones. Nevertheless, this remains a formidable challenge for all existing nuclear models. Physicists are seeking ways to incorporate as many effects as possible in predicting nuclear masses. The recent surge in the popularity of machine learning (ML) has driven significant advancements across various fields of physics [154,155,156,157]. Given their critical importance, numerous machine learning approaches have been applied to study nuclear masses, addressing the demands of nuclear mass predictions in relevant research fields. These approaches include radial basis function (RBF) [158,159,160,161,162], Bayesian neural network (BNN) [163,164,165], kernel ridge regression (KRR) [166,167,168,169,170,171,172,173,174], Gaussian process regression [175,176,177], Bayesian classifier [178], decision tree [179, 180], principal component analysis [181, 182], and others. We introduce some of these methods in what follows, with special emphasis on recent applications of the KRR approach to the RCHB mass table.
The RBF is a handiness machine learning approach widely used for interpolation and extrapolation. It was first introduced to study nuclear masses in Refs. [158, 159], achieving an accuracy of \(\sim 200\) keV. Subsequently, the odd-even effect was incorporated, leading to the RBFoe approach [160,161,162]. The RBFoe method achieved its best accuracy of 135 keV by reconstructing the nuclear mass residuals between the WS4 mass model [38] and experimental data [21]. Note that the accuracies here refer to the rms deviations between the RBF(oe) predictions and the experimentally known nuclei masses in AME2012 [183] with \(Z,N\ge 8\). These results demonstrate the potential of machine learning to improve the description of nuclear masses, as even a simple model like RBF can yield significant improvements.
The BNN is a state-of-the-art machine learning approach that is significantly more sophisticated than the RBF. By combining the strengths of Bayesian statistics and neural networks, the BNN has been employed to enhance nuclear mass predictions in various models [163, 164, 184]. In particular, incorporating additional physical features into the input layer of the neural network, such as quantities related to nuclear pairing and shell effects, has proven highly effective in further improving its performance in mass predictions [164]. This demonstrates the critical role of physical guidance in optimizing BNN predictions. Furthermore, the theoretical accuracies have been significantly improved not only for nuclear masses but also for single-nucleon separation energies. Recently, the Bayesian Machine Learning (BML) mass model was proposed [165], which learns the mass surface of even-even nuclei and their correlation energies with neighboring nuclei. This model achieves an accuracy of 84 keV, i.e., the rms deviation between the BML predictions and the experimentally known nuclei masses in AME2016 [185] with \(Z,N\ge 8\), surpassing the 100 keV threshold in the experimentally known region. The uncertainties of the BML predictions are systematically evaluated, increasing by approximately 50 keV per step along the isotopic chains as one moves into the unknown region. The shell structures in the known region are successfully captured, and several key features in the unknown region are predicted, such as new magic numbers around \(N=40\), the robustness of the \(N=82\) shell, and the weakening of the \(N=126\) shell [165].
The KRR is a powerful and efficient machine learning technique that integrates the principles of ridge regression with the kernel trick, offering a convenient approach for modeling non-linear data. In the KRR, input data are mapped into a higher-dimensional feature space via a kernel function, enabling the capture of complex relationships between variables. The regularization term in ridge regression mitigates overfitting, enhancing the robustness of the KRR for both interpolation and extrapolation. Its capacity to handle high-dimensional data and its flexibility in selecting various kernel functions render the KRR a versatile tool across diverse scientific and engineering applications. The KRR approach was first introduced to improve nuclear mass predictions in Ref. [166], where it was demonstrated to mitigate the risk of deteriorating predictions for nuclei at large extrapolations. Subsequently, the extended KRR approach was developed that incorporates odd-even effects, called the KRRoe approach [167]. This method achieved the most precise machine-learning description of nuclear masses at the time. Furthermore, a multitask learning framework for nuclear masses and separation energies, known as gradient kernel ridge regression, was developed by incorporating gradient kernel functions [169]. Recently, the anisotropic kernel was introduced in the KRR approach, which strengthens the correlation among nuclei with the same neutron number or those with the same proton number and further improves the mass predictions [172]. The successful applications of the KRR approach in nuclear masses [166, 167, 169, 172,173,174] have also spurred its applications in other areas of nuclear physics, such as energy density functionals [186, 187], charge radii [188, 189], and neutron-capture cross sections [190].
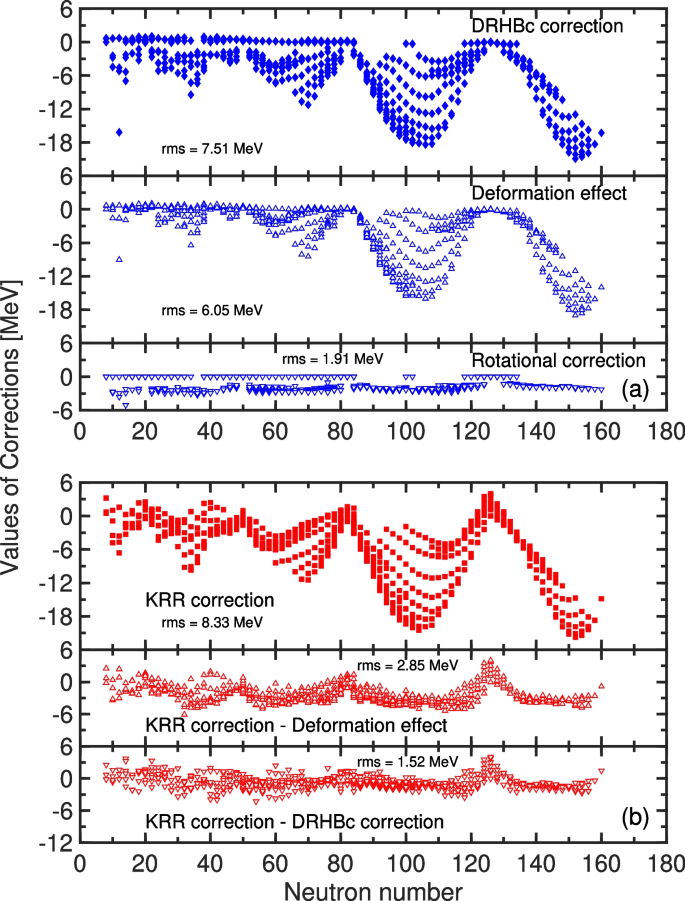
While machine learning approaches are often combined with sophisticated phenomenological models to develop high-precision nuclear mass models that reproduce fairly well experimentally known masses, combinations with microscopic models can help elucidate the physical effects captured by machine learning [170] and provide a more reliable foundation for extrapolating to experimentally unknown regions. In this regard, the KRR approach has been recently applied to refine the RCHB mass table by learning and representing the mass residuals of the RCHB model with respect to experimental data [173, 174]. The goal was to integrate the RCHB theory with the KRR approach to develop a high-precision and reliable nuclear mass model capable of describing both stable nuclei and weakly bound neutron-rich exotic ones. The DRHBc mass table for even-even nuclei was employed to analyze the physical effects incorporated in the KRR corrections and to validate the KRR extrapolations. Shown in Fig. 3a and b are the DRHBc and KRR corrections to the RCHB predictions, respectively. It is evident that the patterns of the KRR and DRHBc corrections are strikingly similar, suggesting that the KRR corrections are predominantly influenced by deformation effects. The residual KRR corrections, obtained by subtracting the intrinsic deformed mean-field corrections in the DRHBc theory, are illustrated in Fig. 3b, with an rms value of 2.85 MeV. A portion of the corrections are undoubtedly attributed to the rotational corrections arising from beyond-mean-field effects for deformed nuclei. The residual KRR corrections, after further subtracting these rotational corrections, are depicted in Fig. 3b, with an rms value of 1.52 MeV. These remaining corrections exhibit a slight parabolic behavior between closed shells, indicating that they still include some deformation effects that are not fully considered by the DRHBc theory, e.g., triaxiality [148]. Certainly, the remaining corrections may also include other effects beyond the scope of the DRHBc theory, such as the beyond-mean-field vibrational corrections and the effects of exchange correlations. It was concluded [173] that the primary contributions to the KRR corrections arise from the deformation effects at the mean-field level, with the beyond-mean-field rotational corrections also playing a significant role. The ultimate accuracy of the RCHB + KRR mass model in reproducing the existing mass data is 385 keV with respect to the experimentally known nuclei masses in AME2020 [21] with \(Z,N\ge 8\).
a The full DRHBc corrections on the RCHB predictions, the DRHBc corrections from the deformation corrections of the intrinsic mean field, and the DRHBc corrections from the rotational corrections from the beyond mean-field effects. b The KRR corrections on the RCHB predictions, the differences between the KRR corrections and the intrinsic deformation effects in the DRHBc corrections, and the differences between the KRR corrections and the full DRHBc corrections. Taken from Ref. [173]
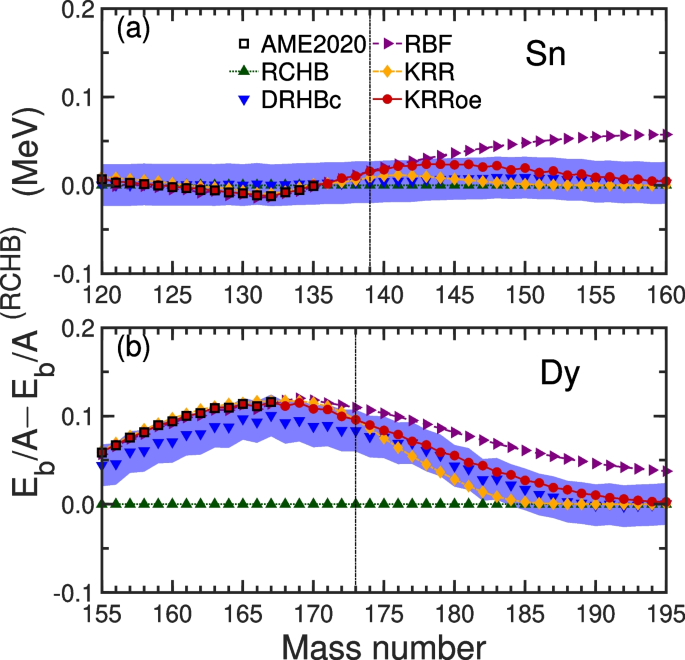
After the release of the DRHBc mass table for even-Z nuclei [112], it is utilized to validate the extrapolation performance of the KRR and KRRoe approaches [174]. The comparison of the RCHB, DRHBc, KRR, and KRRoe mass predictions for tin and dysprosium isotopes is presented in Fig. 4. For both isotopic chains, the KRR and KRRoe predictions closely reproduce the experimental data in the known regions and align well with the DRHBc predictions, even at large extrapolation distances. This demonstrates the reliability of the KRR and KRRoe extrapolations, which have been rigorously examined in Refs. [166, 167]. It is important to note that both the KRR and KRRoe predictions gradually converge to the RCHB predictions, due to the decay behavior of the Gaussian kernel that helps the KRR and KRRoe approaches to avoid deteriorating mass predictions at large extrapolation distances. One can observe that the KRRoe predictions exhibit a farther extrapolation distance than the KRR ones before converging to the RCHB predictions; namely, 160Sn and 196Dy in the KRRoe, compared to 150Sn and 186Dy in the KRR. Note that the DRHBc theory underestimates the experimental binding energies of Dy isotopes, i.e., the experimental results locate on the upper bound of the uncertainty band of the DRHBc predictions. Given the robust DRHBc description for the isospin-dependence of binding energies [102], this underestimation tendency would be consistent along the Dy isotopic chain beyond the experimentally known region. Therefore, the KRRoe prediction keeping upon the DRHBc results in the extrapolated region is reasonable, demonstrating the effectiveness of incorporating odd-even effects in nuclear mass predictions. Finally, the description accuracy for the experimental mass data is further improved from 385 keV by the RCHB + KRR approach to 177 keV by the RCHB + KRRoe approach.
The deviations of binding energy per nucleon \(E_b/A\) in the RCHB, DRHBc, RBF, KRR, and KRRoe predictions, as well as the experimental data [21], from the RCHB results \(E^{(\text {RCHB})}_b/A\) for Sn (a) and Dy (b) isotopes. The purple band represents the uncertainty of nuclear masses in the DRHBc model, evaluated by its rms deviation from the experimental data. The vertical bar in each panel shows the last experimentally known nucleus [191]. Taken from Ref. [174]
The methods introduced above are all supervised machine learning approaches. Unsupervised machine learning studies of nuclear masses also exist, one of which is principal component analysis (PCA). PCA is a widely used statistical technique for feature selection and dimensionality reduction [192, 193]. It transforms the original data into a new set of uncorrelated variables, known as principal components, which are orthogonal in the feature space and ordered by their importance. This allows for the retention of the most significant information while discarding less relevant dimensions. As is well known, various nuclear mass models have been developed. Different models incorporate varying degrees of specific effects. Some models adequately consider certain important effects, while others focus on different aspects. Given the abundance of nuclear mass models, one might ask: can we extract the major patterns underlying these models? Furthermore, can we enhance nuclear mass predictions by recombining these extracted patterns? Two recent studies [181, 182] have explored the application of PCA to nuclear masses, addressing these two questions. The studies found that PCA effectively extracts the principal features embedded in nuclear mass models. The effects from different models are reintegrated and reorganized into a set of extracted principal components. These components can then be recombined to construct new nuclear mass models. In Ref. [181], a direct superposition method was employed, where coefficients were assigned based on the overlap of principal components with experimental data. It was found that incorporating only the first three principal components can already achieve a precision superior to those of all six original theoretical mass models. In Ref. [182], the PCs were utilized as building blocks within the Bayesian Model Combination (BMC) framework. The study revealed that by incorporating model orthogonalization into the proposed BMC framework, one can achieve both improved prediction accuracy and excellent uncertainty quantification performance.
4 Summary and perspective
Precision measurements and reliable predictions of nuclear masses have profound implications across multiple research domains, including nuclear physics and astrophysics. We review the construction of a microscopic relativistic nuclear mass table that incorporates simultaneously deformation and continuum effects using the DRHBc theory, along with the refinement of nuclear mass predictions through the application of the KRR machine learning approach.
Since its inception in 2010, the DRHBc theory has made great success in describing various nuclear phenomena and has demonstrated robust predictive power. In 2018, an international collaboration was established to build a reliable nuclear mass table based on the DRHBc framework. To date, the DRHBc mass table for even-Z nuclei with \(8 \leqslant Z \leqslant 120\) has been released. As one of the most accurate density-functional descriptions, the present DRHBc mass table achieves an impressive accuracy of 1.433 MeV in reproducing existing mass data. Importantly, the table has facilitated diverse applications, spanning the interpretation of experimental observations, the prediction of novel phenomena, and the development of theoretical methods. Thus, the DRHBc mass table has evolved beyond a mere data repository. The complete DRHBc mass table, including odd-Z nuclei, is expected to be available soon, with more relevant applications underway.
Future improvements to the DRHBc description for nuclear masses can be explored in several aspects. First, the 2DCH approach, which better incorporates beyond-mean-field correlation energies than the cranking approximation, has been implemented in the DRHBc theory for even-even nuclei. Extending this approach to odd nuclei and performing global calculations across the nuclear chart would be highly beneficial. Currently, the blocking effects in odd nuclei are addressed through the equal filling approximation in the DRHBc mass table. A rigorous treatment can be achieved using the TODRHBc theory, which would improve both the mean-field description and the rotational correction energy. Additionally, the DRHBc theory considers only axial deformation degrees of freedom. Incorporating triaxiality via the TRHBc theory would further refine the description of certain nuclei. While large-scale TRHBc calculations searching triaxial nuclei would be more computationally demanding than the DRHBc mass table, combining the TRHBc theory with the optimized DWS basis offers a promising way to reducing computational costs. Lastly, machine learning methods, which have already demonstrated significant success in nuclear mass predictions, can be applied to further improve the DRHBc mass table.
The KRR approach as a widely used machine learning technique has been employed to refine the RCHB mass table, with KRR corrections and extrapolations examined by comparison with the DRHBc mass table. The KRR approach significantly improves the accuracy of the RCHB mass table, reducing the rms deviation with respect to experimental data from a few MeV to 385 keV. This substantial improvement corresponds largely to the deformation effects neglected in the RCHB theory, along with rotational corrections and some effects beyond the scope of the DRHBc theory. Notably, the KRR approach demonstrates reliable predictive power within a certain extrapolation distance beyond the experimentally known region, with the advantage of avoiding the risk of deteriorating mass predictions at larger extrapolations. Furthermore, the integration of the KRR approach with odd-even effects into the RCHB mass table yields an even greater improvement in accuracy, reaching 177 keV, and extends the extrapolation range with reasonable predictions compared to the original KRR approach. Once the complete DRHBc mass table becomes available, a combined DRHBc + KRRoe mass model can be developed, which would not only provide an accurate description of known nuclear masses but also offer reliable predictions for unknown ones.
Finally, it is essential to exercise caution when applying machine learning methods, particularly in extrapolations. Various validation techniques exist for machine learning approaches, applicable to both interpolation and extrapolation. Validating any machine learning-based method before using it for predictions is crucial to ensure the reliability of the results and evaluate the associated uncertainties. Extending the reliable extrapolation range of current machine learning methods by integrating them with microscopic theories remains a significant and valuable area of long-term research.