The groundbreaking discovery of unexpectedly high critical temperature (Tc) superconductivity in the Ba–La–Cu–O system in 1986 inaugurated a new high-Tc era of superconductivity [1], a field that continues to thrive and captivate researchers to this present day. Over the past three decades, the exploration of more than 200 cuprate superconductors has revealed a wealth of phenomena extending beyond the realm of zero-resistivity transitions [2]. However, amidst this diversity, a ubiquitous structural thread binds these superconductors together—the presence of CuO₂ planes sandwiched between charge reservoir layers. Notably, the critical temperatures of the major cuprate families, distinguished by their unique charge reservoir layers, exhibit a consistent trend: Tc demonstrates a parallel relationship with the number of CuO₂ layers within the unit cell, peaking at three layers before gradually declining [3,4,5]. From this pattern, we assert with confidence that the CuO₂ layer stands as the heart of high-Tc superconductors, holding the key to unraveling the mysteries of high-Tc superconductivity.

Simultaneously, as the landscape of cuprate superconducting materials expanded, experimental measurement technology advanced rapidly, sweeping through high-Tc superconductivity research like a powerful wind. As representatives of surface-sensitive measurement technologies, scanning tunneling microscopy/spectroscopy (STM/S) and angle-resolved photoemission spectroscopy (ARPES) play pivotal roles in this progression [6, 7]. These technologies contribute to the exploration of pairing symmetry, exotic pseudogap phase, electronic inhomogeneity, nematicity, and various charge/spin orders [8,9,10,11,12]. Unfortunately, all the aforementioned studies were conducted on the charge reservoir layers—the natural cleavage surface of cuprate compounds—rather than the CuO₂ layer—the core of superconductivity. Beyond the CuO₂ planes, the interfaces between the CuO₂ layers and charge reservoir layers also intrigue us, as interface superconductivity serves as a crucial mechanism in certain oxide-containing superconducting systems, such as LaAlO₃ (LAO)/SrTiO₃ (STO) [13], FeSe/STO [14, 15], and, of course, the cuprates [16, 17]. Therefore, obtaining the CuO2-terminated surface could potentially unearth the physics concealed by the charge reservoir layers. In the case of typical materials like Bi₂Sr₂Ca_n-1Cu_nO_2n+4+δ (BSCCO), the CuO₂ surface can be exposed through top-down Ar⁺ ion bombardment or constructed through bottom-up growth, on which the structure of superconducting energy gaps demonstrates exceptionally distinct features compared to those on the charge reservoir layers [18,19,20,21].

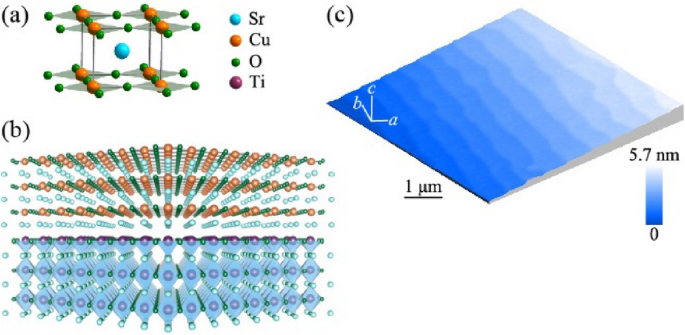
In addition to the artificially constructed CuO₂ surface, synthesis of intrinsic cuprate compounds terminated with a CuO₂ surface promises to reveal more essential properties about high-Tc superconductivity and offer more tunable degrees of freedom. The infinite-layer (IL) Sr_1-xLn_xCuO₂ (Ln = La, Nd, Eu…) compounds emerge as the best candidates among the plethora of cuprates. Structurally, IL compounds boast the simplest configuration with alternative CuO₂ layers and Sr/Ln layers, resembling the limiting case as n tends to infinity in the BSCCO family (Fig. 1a). Due to the absence of apical oxygen atoms, IL compounds terminate with a CuO₂ surface instead of the usual BiO surface [22]. In the parent compound SrCuO₂ (SCO), with partial substitution of Sr by trivalent La³⁺ and Nd³⁺ ions, electron-type superconductivity is induced with a maximum transition temperature of T_c = 43 K and many distinct properties compared to the hole-doped counterpart [23,24,25,26]. Given the rich features of IL cuprates, especially their unique CuO₂ termination surface, they provide us an excellent opportunity for directly probing cuprate superconductivity on the CuO₂ surface.

This article endeavors to furnish a comprehensive review of the STM observations on the CuO₂ surface of IL cuprates. Initially, we delve into the controllable growth and surface structure of IL cuprates. Subsequently, our focus extends to two key aspects. The first centers on Mott physics arising from the variation in the doping levels, while the second explores the superconducting gap structure measured directly on the CuO₂ surface. These results are significantly different from past observations in the charge reservoir layers. Finally, we conclude with reflections and future prospects regarding studies on the CuO₂ surface. Our objective is not only to inspire interest in the exploration of physics directly on the CuO₂ surface but also to provide insights for newcomers entering this esteemed field.

The synthesis of IL cuprate SCO is much more intricate than its structure might suggest. In reality, it exists as a thermodynamically metastable compound amid a landscape of competing phases such as Sr₂CuO₃, Sr₁₄Cu₂₄O₄₁, and orthorhombic SrCuO₂ [27, 28]. The pursuit of a single crystal of this compound proves elusive for its bulk material; only powder forms of polycrystal samples have been successfully synthesized using high-pressure techniques [29, 30]. Thin-film growth provides a practical approach to acquiring high-quality single-crystal IL samples, achievable through both pulsed laser deposition (PLD) [31,32,33] and molecular beam epitaxy (MBE) [34,35,36]. The epitaxial strain imposed by substrates significantly modulates superconductivity in these films. Unlike hole-doped cuprates, which benefit from compressive strain [37], electron-doped systems exhibit enhanced Tc under tensile strain [34, 38]. The tensile strain expands the in-plane lattice parameter, thereby strengthening electron–electron correlations in the Cu \({d}_{{x}^{2}-{y}^{2}}\) orbits due to bandwidth narrowing, and the accompanying out-of-plane compression via the Poisson effect helps suppress the detrimental influence of apical oxygen [25]. Consequently, substrates with larger in-plane lattice parameters than SCO (3.927 Å) are typically employed in their film growth, such as KTaO₃ (3.989 Å) and DyScO₃ (3.944 Å). However, the commonly used conductive oxide substrate, Nb-doped (STO), which is compatible with STM measurements, possesses a smaller in-plane lattice parameter (3.905 Å) (Fig. 1b), posing a challenge in studying the superconducting CuO₂ surface by STM.

To overcome this challenge, rare-earth dopants with smaller ionic radii have proven effective in realizing superconductivity in Sr_1-xLn_xCuO₂/STO films, ranging from La³⁺ [39], Nd³⁺ [40], to Eu³⁺ [41, 42]. The uniform atomic step-terrace topography of the Sr_1-xEu_xCuO₂ (SECO)/STO films is shown in Fig. 1c. In the lanthanide series, as the atomic number increases, the cation radius decreases, and, concurrently, the basicity also gradually diminishes. This implies that a greater number of doping ions are required to achieve the same effective electron concentration. Hence, the optimal choice of dopant elements should be a delicate compromise between the cation radius and the doping capability.

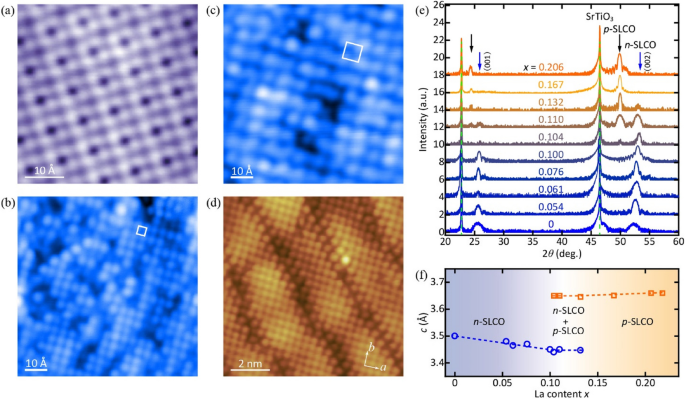
The surface structure of IL cuprates undergoes various modifications in response to changes in the doping level, offering a distinctive fingerprint for their doping situation. In the growth of Sr_1-xLa_xCuO_2+y (SLCO) films, the stoichiometric parameter x can be precisely calibrated by the La/Sr flux ratio using a quartz crystal microbalance. In the pristine state, the undoped SCO parent compound manifests a (2 × 2) superstructure on its surface, shown in Fig. 2a [43]. This surface reconstruction is driven by the polar catastrophe [44], a consequence of the assumed diverging potential resulting from the alternating stacking of positively charged Sr²⁺ layers and negatively charged CuO²⁻ layers. Consequently, oxygen atoms on the surface exhibit an upward and downward shift relative to the CuO₂ plane with a C₂ symmetry, to counterbalance the accumulated potential. Upon the introduction of rare-earth dopants beyond a critical level (x > 0.054), free charge in the bulk naturally screens the polar discontinuities, resulting in a pristine 1 × 1 CuO₂ surface (Fig. 2b) [39]. The smaller ionic radii of rare-earth dopants compared to Sr²⁺ drive a reduction in the lattice parameter along the c-axis with increasing dopant concentration until a structural transition occurs.

In the case of La-doped IL films, a long-c phase emerges for x > 0.11, leading to a larger c ~ 3.65 Å due to the partial intake of apical oxygens in the Sr/La layers [34, 38, 39]. The long-c phase displays a (2 × 2) superstructure owing to the periodic occupation of apical oxygens (Fig. 2c), resulting in a change of dominating carriers from n-type (electron) to p-type (hole). This transition provides a valuable opportunity to investigate doping evolution in both the electron-doped and hole-doped regimes [39]. The intricate incorporation of oxygen atoms into the SLCO compound unfolds with particular complexity. In SLCO films grown on the SrRuO₃ (SRO)-buffered STO substrates, some interstitial oxygen atoms are introduced in a few surface layers, leading to a supermodulated surface topography (Fig. 2d) [45]. In addition to STM topography, the doping level can also be probed via c-axis length measurements from x-ray diffraction (XRD), where c decreases with x in the electron-doped regime, followed by an abrupt increase upon entering the hole-doped regime (Fig. 2e, f). The surface topography and crystal structure of IL cuprates correlate closely with the quantity of rare-earth dopants and introduced oxygen atoms, which also implies distinct properties. Therefore, a well-prepared CuO₂ surface with a well-defined topography forms the groundwork for subsequently exploring the electronic properties afterwards.

A foundational commonality in the electronic properties of cuprate superconductors is their origin from doped Mott insulators [46]. In their parent compounds, the band structure exhibits a charge-transfer gap (CTG) separating the charge-transfer band (CTB) and the upper-Hubbard band (UHB). A comprehensive understanding of the Mott band structure evolution with doping is crucial for unraveling the underlying mechanisms of high-Tc superconductivity. However, the experimental observations on this matter remain a subject of ongoing debate. One scenario suggests that doping triggers a discernible transfer of spectral weight from the high- to low-energy states, effectively pinning the Fermi energy (E_F) within the CTG [47,48,49]. Conversely, certain ARPES observations indicate that E_F shifts concerning the CTB at different doping levels [50,51,52]. The apparent ambiguity in these results is partly attributed to limited and discontinuous doping levels. More significantly, all these measurements are conducted in various charge reservoir layers, rather than the common CuO₂ layers, adding complexity to the interpretation of the findings.

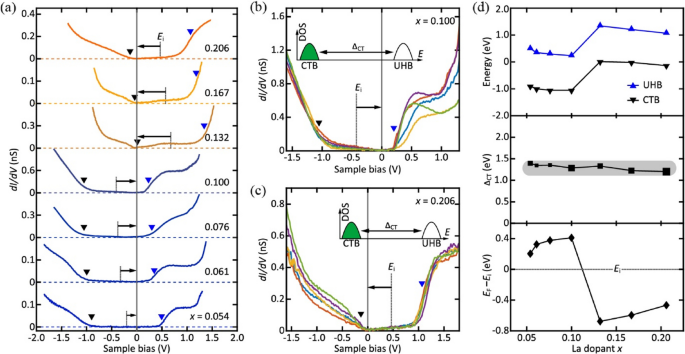
STM investigation directly in the CuO₂ surface of MBE-grown IL films yields clearer insights into the evolution of the Mott band with doping. The averaged density of states (DOS) of CuO₂ planes across various doping levels (Fig. 3(a)) reveals the remarkable stability of the fundamental Mott–Hubbard bands, while E_F systematically shifts with each doping increment. A meticulous examination, comparing the electronic DOS with the schematic band structure in n-SLCO and p-SLCO (Fig. 3b and c), consistently exposes the existence of a CTG between the CTB and the UHB. Figure 3d displays the onset energies of CTB and UHB as a function of the La dopant concentration (x), revealing a constant difference denoted as the CTG magnitude Δ_CT of 1.30 ± 0.07 eV. The most significant change is the shift of E_F relative to the midgap energy E_i. In the n-type regime (x ≤ 0.100), E_F gradually moves away from E_i and towards UHB. However, a pivotal moment occurs at x = 0.132, where E_F abruptly drops below E_i, converging towards CTB due to the incorporation of apical oxygens. Subsequently, in the p-type regime, an upward shift in E_F results from the increasing presence of La donors. Followed by the shift of E_F, the dopant-induced in-gap states (IGS) are observed to overspread the entire CTG at sufficient doping levels (Fig. 3a, b, c). Distinct from the peak- or humplike electronic DOS observed in the charge reservoir layers [48, 49, 53], the continuum of IGS implies the existence of a confined two-dimensional (2D) electron or hole liquid at Sr_1-x(La)_x/CuO_2+y interfaces or evanescent states within the CTG of CuO₂ [54].

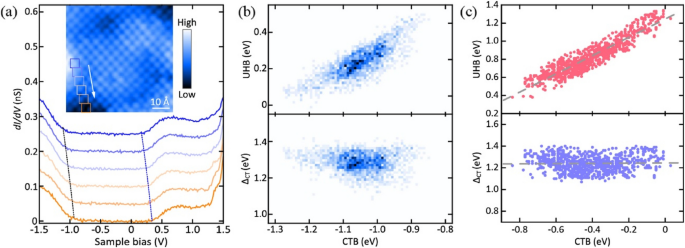
Beyond the global perspective offered by averaged spectra for each doping level, examining local electronic DOS at the atomic scale further enhances the understanding for the Mott transition. Single-atom defects are discerned on the atomically resolved Sr_1-xNd_xCuO₂ (SNCO) surfaces, including substitutional Nd donors (Nd_Sr), intrinsic acceptors of apical oxygen (O_A), and Cu vacancies (V_Cu) [39]. The impact of these donors and acceptors is localized to a few unit cells, leading to local electronic inhomogeneity on the surface. Figure 4a and b shows this inhomogeneity in SNCO, where the overall Mott band structure undergoes minimal change, but the onsets of UHB and CTB shift synchronously due to the variations in local Nd_Sr doping. This local electronic inhomogeneity becomes more pronounced on the supermodulated surface of SLCO/SRO/STO, especially following vacuum annealing, resulting in significant variations in incorporated oxygens (Fig. 4c) [45]. Despite a continuous shift of E_F by up to 0.7 eV, the UHB and CTB onset energies exhibit a positive correlation with a slope close to unity.

When viewed from the CuO₂ planes, the Mott band evolutions of all the IL compounds consistently adhere to a unifying pattern, irrespective of dopants in the underlying charge reservoir layers. This observation leads to a reasonable speculation that the CuO₂ planes of all the cuprate materials conform to the same pattern. Phenomenologically, this pattern draws parallels to the modulation doping observed in Al_xGa_1-xAs/GaAs semiconductor heterostructures [55], where the roles of the valence and conduction bands in undoped GaAs mirror the CTB and UHB in chemically undisturbed CuO₂. Notably, the separation of ionized dopants in the charge reservoir layers and free carriers in CuO₂ occurs within the compound itself, providing the basis for terming this process as self-modulation doping [56]. This picture unravels the complexities of the doped Mott insulator, offering a glimpse into a harmonic symphony of electronic states on the CuO₂ surface.

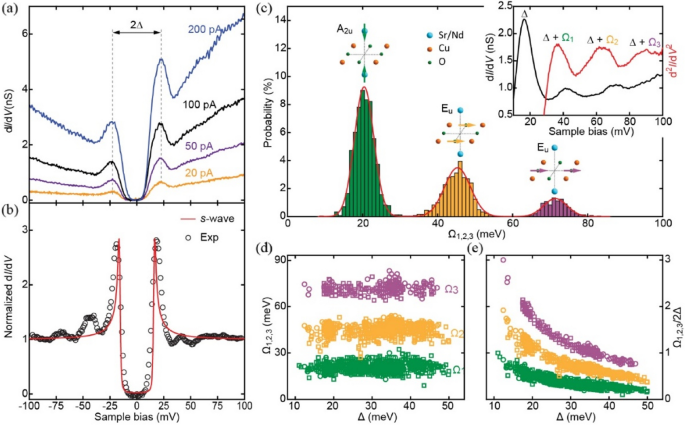
In order to comprehend the mechanism of superconductivity, a fundamental understanding of the interaction binding electrons into Cooper pairs is essential. Such interactions might arise from lattice vibrations, spin excitations, or other bosonic modes. Measurements of low-energy DOS by STS could provide straightforward clues of both the superconducting energy gap (Δ) and bosonic excitation energy (Ω) simultaneously. This is because the bosonic mode often exhibits excitation states by coupling to paired electrons at the energy E = Δ + Ω [57]. Direct observations of these phenomena have been realized in the CuO₂ planes of SNCO [40] and its sister compound Sr_1-xEu_xCuO₂ (SECO) [41].

The distinct superconducting gap structure in SNCO is revealed in Fig. 5a and b, featuring pronounced coherence peaks and a complete absence of DOS between them—hallmarks of fully gapped superconductivity. These full gaps remain robust across changes in the tip-to-sample distance (Fig. 5a) and can be accurately fitted using the Dynes model with a single s-wave gap function [58], confirming their nodeless nature. These findings align with previous tunneling and ARPES results in SLCO [24, 26] yet offer superior quality and clarity. Notably, they deviate significantly from the nodal d-wave gap function observed on the charge reservoir planes of various hole-doped cuprates. Beyond IL films, STM investigations on the superconducting CuO₂ planes in other systems also indicate the consistent nodeless patterns [20, 59, 60]. Thus, a critical reassessment of the role of charge reservoir layers in tunneling measurements of cuprates is imperative, seeking to determine whether the nodeless electron pairing is a generic feature of the CuO₂ planes in cuprate superconductors.

Outside the superconducting gap of SNCO, multiple peak-dip-hump features are frequently observed, signifying the coupling between bosonic modes and superconductivity. The characteristic energies of these excitation states manifest as three inharmonic values: Ω_1,2,3 = 20, 45, and 72 meV (Fig. 5c). Remarkably, these energies align coincidentally with the external, bending, and stretching phonon mode energies obtained from the optics [61] and Raman [62] measurements in bulk SCO. The role of phonons as the pairing glue is further substantiated by examining the relationship between Ω and Δ. The emergence of superconductivity in SNCO and SECO films resembles a three-dimensional percolation process, where superconducting domains are surrounded by nonsuperconducting phases [40, 41]. The substantial inhomogeneity is evident in a wide distribution of Δ in different surface areas. In contrast, the energies of bosonic mode Ω_1,2,3 show little variation against Δ, and the local ratio Ω_1,2,3/2Δ even exceeds unity for small Δ. These findings support lattice vibrations as the bosonic mode but contradict spin excitations, whose energies generally depend on Δ and consistently remain below the pair-breaking energy with Ω/2Δ < 1 [63].

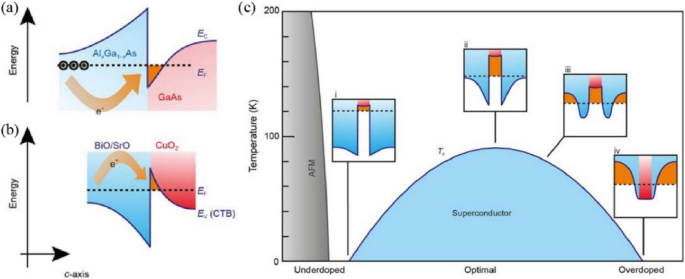
By combining the Mott band transition with doping, the nodeless superconducting gap structure, and the lattice vibrational modes directly measured in the CuO₂ planes of IL cuprates, the hidden physics beneath the charge reservoir layers appears on the verge of revelation. Echoing the nodeless pairing observed in the CuO₂ monolayer grown on BSCCO, the observations in CuO₂ planes collectively suggest a quantum well (QW) scenario induced by self-modulation doping (Fig. 6). In this framework, the charge reservoir layers, despite their intrinsic anisotropic properties, primarily function to create the necessary band bending that forms a QW within the CuO₂ layers—analogous to the formation of two-dimensional electron or hole gases in semiconductor heterojunctions. The rigid Mott band observed experimentally indicates that doping shifts the Fermi level without significantly altering the underlying electronic structure of the CuO₂ planes, thereby preserving a well-defined QW. Within this QW, carriers are confined to a two-dimensional landscape, leading to a simple and nearly isotropic Fermi surface. This isotropy is crucial because it naturally supports uniform pairing interactions—such as those mediated by lattice vibrations—which give rise to a nodeless superconducting gap. Recent studies continue to highlight the importance of interface charge transfer in cuprate systems, such as overdoped La_2-xSr_xCuO₄ (LSCO)/La₂CuO₄ (LCO) heterostructures [64], monolayer LSCO/LAO [65], and LCO/PrBa₂Cu₃O₇ (PBCO) interfaces [66], where the charge transfer mechanism based on QW formation between layers likely plays a critical role in the emergence of superconductivity. Especially in the LCO/PBCO system, the two insulators with well-defined bandgaps can form a perfect QW to capture the two-dimensional holes. In particular, the LCO/PBCO system, comprised of two insulators with well-defined bandgaps, can form an ideal QW to confine two-dimensional holes. Overall, this QW scenario provides a conceptual framework that unifies the effects of electronic confinement, the emergence of clean 2D carriers, and pairing interactions in the development of high-Tc superconductivity.

While decades of research have been dedicated to the exploration of cuprate superconductivity, this review paper introduces a relatively new research perspective with innovative results: STM measurements directly on the CuO₂ planes unveil more profound insights into cuprate superconductivity—specifically the revelation of a universal nodeless superconducting gap. The material systems used for these measurements are the IL Sr_1-xLn_xCuO₂ compounds. We share extensive insights into their controllable growth and surface structure. Two significantly crucial phenomena emerge on their CuO2-terminated surface: one is the doping effect that only systematically shifts E_F without altering the Mott band structure; the other is the nodeless superconducting gap accompanied by phonon-like bosonic modes. These findings lead to a conclusion involving a QW-restrained superconductivity scenario induced by self-modulation doping, fundamentally divergent from outcomes centered on the charge reservoir layers.

Drawing inspiration from this direction, several promising avenues for future exploration come to the forefront. Firstly, investigating oxygen isotope effects could act as the smoking gun to determine the effect of phonons in cuprate superconductivity. Although the overall oxygen isotope effect is ambiguous in cuprates compared to elementary superconductors due to their complex structure [67], it is hopeful to observe significant changes in Δ and Ω directly on the CuO₂ planes following the substitution of O¹⁶ with O¹⁸.

Secondly, the attainment of superconductivity in hole-doped IL cuprate films could serve as crucial backup. Despite consistent Mott transition behavior in both electron- and hole-doped IL films, superconductivity manifests exclusively in the electron regime. Research endeavors targeting hole-doped superconductivity through controllable growth strategies, such as tuning doping levels, altering dopant elements, or transitioning from Sr to Ca in the parent compounds, offer an expansive field for exploration.

Lastly, probing magnetic interactions directly in the CuO₂ planes presents a great opportunity to untangle the relationship between superconductivity and spin orders. An overlap still exists between the antiferromagnetic regime and the superconductivity dome in the phase diagram of electron-doped superconductors [25]. Spin-polarized measurements in the CuO₂ surface could distinguish whether the magnetic orders originate from CuO₂ layers or charge reservoir layers, thereby substantiating the significance or insignificance of considering spin as the pairing glue. This multifaceted approach sets the stage for further advancements in our understanding of cuprate superconductivity.