1 Introduction

An impurity particle interacting with a Fermi bath of non-interacting fermions is a traditional quantum many-body problem (namely, the Fermi polaron problem) [1], appearing in a diverse fields of physics, including condensed matter physics, nuclear physics and ultracold atomic physics. The research on Fermi polarons brings us some fundamental concepts of quantum many-body physics, such as polaron quasiparticles [2], Fermi-edge singularities [3, 4] and Anderson orthogonality catastrophe [5]. Over the past two decades, the Fermi polaron problem receives a renewed interest [6,7,8,9,10,11,12], due to the rapid experimental advances in ultracold atomic physics. Due to the unprecedented controllability with ultracold atoms [13], particularly in tuning the interparticle interaction strength [14] and in creating artificial optical lattices, various textbook models of Fermi polarons can be experimentally realized [12]. The spectral properties of Fermi polarons have now been quantitatively measured, by using radio-frequency spectroscopy [15,16,17], Ramsey interferometry [18], Rabi oscillation [19, 20] and Raman spectroscopy [21], and haven been theoretically investigated, by using various many-body approaches, including variational Chevy ansatz [22,23,24,25,26,27], diagrammatic strong coupling theories [28,29,30,31,32], functional renormalization group [33, 34] and quantum Monte Carlo simulations [35,36,37].

In spite of enormous efforts on studying the Fermi polaron, the quantitive understanding of its spectral properties remains a grand challenge, particularly at finite temperature [32]. In this respect, exact results of Fermi polarons in various limiting cases are highly desirable. There are two well-known such cases. The first case is the heavy polaron limit [4, 7, 38,39,40], where the impurity is infinitely heavy so it can be treated a scattering potential. Another interesting non-trivial limit is the one dimension case with equal mass for the impurity and the Fermi bath, where the Fermi polaron problem can be exactly solved by using the celebrated Bethe ansatz technique for the Gaudin-Yang model [41,42,43,44] and the one-dimensional (1D) Hubbard model [45,46,47]. For a Fermi bath in free space as described by the Gaudin-Yang model, the exact calculation of polaron spectral properties was presented in the pioneering work by Castella and Zotos [43]. Most recently, the case of a 1D Fermi bath in optical lattices, as described by the 1D Hubbard model, has also been discussed by the present authors and collaborators, in the form of a short Letter [48].

In this work, we theoretically investigate the spectral properties of Fermi polarons in 1D lattices, based on the exactly solvable 1D Hubbard model [45,46,47]. The purpose of our work is two-fold. On the one hand, we present the technical details of the exact calculation reported earlier in the brief Letter [48]. In particular, we show in great detail how to derive the impurity form factor, which is important for future studies on the quantum dynamics of particles interacting with a Fermi bath [49,50,51,52]. On the other hand, we extend the theoretical calculations to the case of attractive on-site interaction strength. We show that the two cases of repulsion and attraction are related by a particle-hole transformation for fermions in the Fermi bath. We also discuss the evolution of spectral properties of Fermi polarons with increasing attractive interaction and with varying the filling factor of the Fermi bath. These extended results are useful for future experiments on Fermi polarons in 1D optical lattices.

The rest of the paper is organized as follows. In the next section (Section 2), we briefly overview the Bethe ansatz solution of the 1D Hubbard model with only one spin-down impurity. In Section 3, we derive the form factor of the regular Bethe wavefunctions. In Section 4, we discuss the irregular quantum states that cannot be covered in the Bethe ansatz solutions, such as the spin-flip states and the \(\eta\)-pairing states [46, 53]. These irregular states are necessary to include, as they make notable contributions to the impurity spectral function at finite lattice sizes. In Section 5, we present the details of numerical calculations and emphasize how to select the most important many-body states to exhaust the sum rule, as a useful way to check the convergence of our numerical calculations. In Section 6, we discuss the configuration of the many-body states that have significant form factor or residue. We analyze in detail the spectral properties of Fermi polarons at different filling factors and at attractive on-site interaction strengths. Finally, Section 7 is devoted to the conclusions and outlooks.

2 Bethe ansatz solution

We start by considering a highly spin-population imbalanced spin-1/2 Fermi gas in 1D optical lattices with lattice size L, as described by the standard 1D Hubbard model [45,46,47], \(\mathcal {H}=\mathcal {H}_{0}+\mathcal {H}_{U}\), where

\(\begin{aligned} \mathcal {H}_{0} & = -t\sum\limits_{i=1}^{L}\sum\limits_{\sigma =\uparrow ,\downarrow }\left( \psi _{i\sigma }^{\dagger }\psi _{i+1\sigma }+h.c.\right) ,\end{aligned}\)
(1)

\(\begin{aligned} \mathcal {H}_{U} & = U\sum\limits_{i=1}^{L}\psi _{i\uparrow }^{\dagger }\psi _{i\uparrow }\psi _{i\downarrow }^{\dagger }\psi _{i\downarrow }, \end{aligned}\)
(2)

are the non-interacting kinetic Hamiltonian and the interaction Hamiltonian with strength U, respectively. We assume the periodic boundary condition, so \(\psi _{L+1\sigma }\equiv \psi _{1\sigma }\). This model is exactly solvable by using the Bethe ansatz technique for any particle numbers \(N=\sum _{i}\psi _{i\uparrow }^{\dagger }\psi _{i\uparrow }\) and \(M=\sum _{i}\psi _{i\downarrow }^{\dagger }\psi _{i\downarrow }\). We focus on the limit of a single spin-down fermion (\(M=1\)) and treat it as an impurity. The filling factor of the lattice is then given by

\(\begin{aligned} \nu \equiv \frac{N+M}{L}=\frac{N+1}{L}. \end{aligned}\)
(3)

2.1 Bethe ansatz equations

In this case, the many-body states \(\left| \Psi _{N+1,Q}(\{k_{j,}\},\Lambda )\right\rangle\) of the system can be characterized by a set of the quasi-momenta \(k_{j}\) (\(j=1,..,N+1\)) and the quasi-momentum \(\Lambda\), which satisfy \(N+2\) coupled equations [45,46,47],

\(\begin{aligned} \frac{\sin (k_{j})-\Lambda +iu}{\sin (k_{j})-\Lambda -iu} & = e^{ik_{j}L},\end{aligned}\)
(4)

\(\begin{aligned} \prod\limits_{j=1}^{N+1}\frac{\sin (k_{j})-\Lambda +iu}{\sin (k_{j})-\Lambda -iu} & = 1, \end{aligned}\)
(5)

where \(u=U/(4t)\) is the dimensionless interaction parameter. For convenience, we assume that the lattice size L is an even integer, N is an odd integer, and \(L>N\). Once we solve \(k_{j}\) for a particular many-body state, the total momentum and energy of the state are obtained by,

\(\begin{aligned} Q=\sum\limits_{j=1}^{N+1}k_{j}\;\text {mod}\;2\pi \end{aligned}\)
(6)

and

\(\begin{aligned} E_{N+1}\left( \{k_{j}\},\Lambda \right) =-2t\sum\limits_{j=1}^{N+1}\cos k_{j} \end{aligned}\)
(7)

respectively. We restrict the total momentum Q to the first Brillouin zone \((-\pi ,+\pi ]\) and always consider \(Q\ge 0\). We note that, for a single impurity, the quasi-momentum \(\Lambda\) is real. In contrast, a complex-valued pair of the quasi-momenta (i.e., \(k_{1}\) and \(k_{2}=k_{1}^{*}\), for concreteness) may arise for both attractive interaction (\(u<0\)) and repulsive interaction (\(u>0\)), signifying a bound state. These bound states are named as the \(k-\Lambda\) string solutions. For convenience, we refer to the other solutions with real quasi-momenta as the all real-k solutions.

It is useful to rewrite the coupled equations for \(k_{j}\) and \(\Lambda\) into an alternative form [46],

\(\begin{aligned} \sin \left( k_{j}\right) -\Lambda & = u\cot \left( \frac{k_{j}L}{2}\right) ,\end{aligned}\)
(8)
\(\begin{aligned} \sum\limits_{j=1}^{N+1}k_{j} & = n\frac{2\pi }{L}, \end{aligned}\)
(9)

where \(-L/2 is an integer. In the ground state, the total momentum \(Q=0\) and \(n=0\), we must have \(\Lambda =0\), as illustrated in Fig. 1. For a real quasi-momentum \(k_{j}\), for late convenience we introduce the variable [43],

\(\begin{aligned} \delta _{j}=-\frac{\pi }{2}+\arctan \left[ \frac{\sin \left( k_{j}\right) -\Lambda }{u}\right] . \end{aligned}\)
(10)

Fig. 1
figure 1

Graphical illustration of the solutions for \(\sin (k_{j})=u\cot (k_{j}L/2)\) in the ground state, where \(\Lambda =0\). The blue dots and red dots are the roots for the repulsive interaction \(u>0\) and the attractive interaction \(u<0\), respectively


According to the definition of \(\delta _{j}\), it is easy to check that

\(\begin{aligned} e^{-2i\delta _{j}} & = e^{ik_{j}L},\end{aligned}\)
(11)

\(\begin{aligned} \frac{e^{i\delta _{j}}}{\sin \delta _{j}} & = \frac{\sin \left( k_{j}\right) -\Lambda -iu}{-u}. \end{aligned}\)
(12)

For the pair of the complex-valued quasi-momenta \(k_{1}\) and \(k_{2}\), it is worth noting that we need to take care of the use of \(\delta _{1}\) and \(\delta _{2}\). In this case, actually it is more convenient to directly use the complex-valued pair of \(k_{1}\) and \(k_{2}\).

2.2 Impurity spectral function

We are interested in calculating the impurity spectral function of the single spin-down fermion. To this aim, we need to find out the form factor of the many-body states \(\left| \Psi _{N+1,Q}(\{k_{j}\},\Lambda )\right\rangle\), defined by,

\(\begin{aligned} F_{N+1}\left( \{k_{j}\},\Lambda \right) =\left\langle \text {FS}_{N}\left| \psi _{Q\downarrow }\right| \Psi _{N+1,Q}\left( \{k_{j}\},\Lambda \right) \right\rangle , \end{aligned}\)
(13)

which measures the overlap of the many-body state with the product state \(\psi _{Q\downarrow }^{\dagger }\left| \text {FS}_{N}\right\rangle\) (i.e., the product of a single-particle impurity state with momentum Q and a Fermi sea of N non-interacting spin-up fermions). At zero temperature, the impurity spectral function

\(\begin{aligned} A(Q,\omega )=-\frac{1}{\pi }\text {Im}\mathcal {G}(Q,\omega ) \end{aligned}\)
(14)

can be calculated from the Green function,

\(\begin{aligned} \mathcal {G}\left( Q,\omega \right) =\sum\limits_{\{k_{j}\},\Lambda }\frac{Z_{N+1}\left( \{k_{j}\},\Lambda \right) }{\omega -\left[ E_{N+1}\left( \{k_{j}\},\Lambda \right) -E_{\text {FS},N}\right] +i\delta }, \end{aligned}\)
(15)

where \(E_{\text {FS},N}\) is the energy of the fully occupied Fermi sea \(\left| \text {FS}_{N}\right\rangle\) and

\(\begin{aligned} Z_{N+1}(\{k_{j}\},\Lambda )\equiv \left| F_{N+1}(\{k_{j}\},\Lambda )\right| ^{2} \end{aligned}\)
(16)

is the residue. For the finite lattice size L, we introduce a spectral broadening factor \(\delta \rightarrow 0^{\dagger }\) to smooth the discrete energy levels of many-body states. A typical choice is the average single-particle spectral interval, \(\delta =4t/L\), where 4t is the band width of the 1D Hubbard model.

We note that, the summation in the Green function \(\mathcal {G}(Q,\omega )\) is over all the many-body states of the system. These includes both the regular Bethe wavefunctions \(\left| \Psi _{N+1,Q}(\{k_{j}\},\Lambda )\right\rangle\) that can be constructed from the Bethe ansatz solutions with finite quasi-momenta \(\{k_{j}\}\) and \(\Lambda\) [46], and some irregular states that we will discuss in detail in Section 4.

We note also that, the spectral function satisfies the sum-rule \(\int _{-\infty }^{+\infty }d\omega A(Q,\omega )=1\), as a result of the completeness of the many-body states, i.e.,

\(\begin{aligned} \sum\limits_{\{k_{j}\},\Lambda }Z_{N+1}\left( \{k_{j}\},\Lambda \right) =1. \end{aligned}\)
(17)

As we shall see, this sum-rule is very useful to check the convergence of our numerical calculations.

2.3 Particle-hole transformation

The one-dimensional Hubbard model has an interesting particle-hole transformation, which allows us to change the sign of the on-site interaction strength [47]. To see this, let us consider the following transformation to the field operators \(\psi _{i\uparrow }\) and \(\psi _{i\uparrow }^{\dagger }\) for the Fermi bath of spin-up fermions, \(\psi _{i\uparrow }\rightarrow (-1)^{i}\psi _{i\uparrow }^{\dagger }\) and \(\psi _{i\uparrow }^{\dagger }\rightarrow (-1)^{i}\psi _{i\uparrow }\). There is no change to the field operators for the spin-down impurity. This is indeed a particle-hole transformation for the Fermi bath, as the local density operator of spin-up fermions changes as,

\(\begin{aligned} \psi _{i\uparrow }^{\dagger }\psi _{i\uparrow }\rightarrow (-1)^{i}\psi _{i\uparrow }(-1)^{i}\psi _{i\uparrow }^{\dagger }=1-\psi _{i\uparrow }\psi _{i\uparrow }^{\dagger }. \end{aligned}\)
(18)

Therefore, in the thermodynamic limit (\(L\rightarrow \infty\)) the filling factor changes from \(\nu =\sum _{i}\psi _{i\uparrow }^{\dagger }\psi _{i\uparrow }/L\) to \(\sum _{i}(1-\psi _{i\uparrow }^{\dagger }\psi _{i\uparrow })/L=1-\nu\).

Under such a particle-hole transformation, the non-interacting Hamiltonian is invariant, since the local hopping term \(-t\psi _{i\uparrow }^{\dagger }\psi _{i+1\uparrow }+h.c.\rightarrow -t\left( -1\right) ^{i}\psi _{i\uparrow }\left( -1\right) ^{i+1}\psi _{i+1\uparrow }^{\dagger }+h.c.=-t\psi _{i+1\uparrow }^{\dagger }\psi _{i\uparrow }+h.c.\) does not change. Here, the minus sign due to the exchange of the fermionic field operators is cancelled by the factor \((-1)^{i}(-1)^{i+1}=-1\). On the other hand, we should have \(\psi _{i\uparrow }^{\dagger }\psi _{i\uparrow }\psi _{i\downarrow }^{\dagger }\psi _{i\downarrow }\rightarrow (1-\psi _{i\uparrow }^{\dagger }\psi _{i\uparrow })\psi _{i\downarrow }^{\dagger }\psi _{i\downarrow }\) and hence,

\(\begin{aligned} {\mathcal {H}}_{U}\rightarrow U\sum\limits_{i}(1-\psi _{i\uparrow }^{\dagger }\psi _{i\uparrow })\psi _{i\downarrow }^{\dagger }\psi _{i\downarrow }=\mathcal {H}_{-U}+U. \end{aligned}\)
(19)

It is clear that the on-site interaction Hamiltonian changes its sign (\(U\rightarrow -U\)). Additionally, we have an unimportant constant energy shift \(+U\).

Therefore, with the particle-hole transformation for the spin-up Fermi sea, the impurity problem with a positive on-site interaction \(U>0\) at the filling factor \(\nu\) is identical to the problem with an attractive on-site interaction \(-U<0\) at the filling factor \(1-\nu\).

3 The form factor

We now derive the expression of the form factor \(F_{N+1}\left( \{k_{j}\},\Lambda \right)\) for Bethe wavefunctions. In the first quantization, the real-space wavefunction of the product state \(\psi _{Q\downarrow }^{\dagger }\left| \text {FS}_{N}\right\rangle\) can be easily written down in terms of a \(N\times N\) Slater determinant,

\(\begin{aligned} \psi _{Q\downarrow }^{\dagger }\left| \text {FS}_{N}\right\rangle =\frac{1}{\sqrt{N!}}\sqrt{\frac{1}{L}}e^{iQx_{\downarrow }}\det _{1\le j,m\le N}\left( \sqrt{\frac{1}{L}}e^{iq_{j}x_{m}}\right) , \end{aligned}\)
(20)

where \(x_{m}\) is the position of the N spin-up fermions and

\(\begin{aligned} q_{j}=\left[ -\frac{N+1}{2}+j\right] \frac{2\pi }{L} \end{aligned}\)
(21)

is the associated momentum, which takes the values \([-(N-1)/2,\cdots ,-1,0,1,\cdots ,+(N-1)/2](2\pi /L)\) at zero temperature. In contrast, the expression of the Bethe ansatz wavefunction \(\left| \Psi _{N+1,Q}(\{k_{j}\},\Lambda )\right\rangle\) is much more involved.

Let us start from the general form of the nested Bethe ansatz in the region \(R=\{x_{R0},\cdots x_{RN}\}\) with \(x_{R0} [46, 47]:

\(\begin{aligned} \left| \Psi _{N+1,Q}(\{k_{j}\},\Lambda )\right\rangle \propto \sum _{P\in S_{N+1}}A\left( R;P\right) e ^{i\sum _{j=0}^{N}k_{Pj}x_{Rj}}. \end{aligned}\)
(22)

Here, R is a permutation of the \(N+1\) coordinates \(\{x_{\downarrow },x_{1},x_{2},\cdots ,x_{N}\}\) and \(P=\{P0,\cdots ,PN\}\) is a permutation of the \(N+1\) quasi-momenta \(\{k_{1},k_{2},\cdots ,k_{N+1}\}\) in the permutation group \(S_{N+1}\). It is convenient to focus on the fundamental region \(R=\{x_{\downarrow }, where the coefficients \(A\left( R;P\right)\) takes the following form (see the page 205 of Ref. [46]),

\(\begin{aligned} A\left( R;P\right) & =\epsilon \left( P\right) \prod _{j=1}^{N}\left[ \frac{\sin \left( k_{Pj}\right) -\Lambda -iu}{-u}\right] ,\end{aligned}\)
(23)

\(\begin{aligned} & =\epsilon \left( P\right) \prod _{j=1}^{N}\frac{e^{i\delta _{Pj}}}{\sin \delta _{Pj}}, \end{aligned}\)
(24)

up to an un-important normalization factor, which we shall determine later. We have used \(\epsilon (P)=\pm 1\) to denote the parity of the permutation P, so for an even permutation \(\epsilon (P)=+1\) and for an odd permutation \(\epsilon (P)=-1\).

The key idea of deriving the form factor is to rewrite the Bethe wavefunction \(\left| \Psi _{N+1,Q}(\{k_{j}\},\Lambda )\right\rangle\) into a \(N\times N\) Slater determinant [42, 54]. Once we find it, the calculation of the form factor, i.e., the overlap of two \(N\times N\) Slater determinants, can be easily carried out by using the celebrated identity [55],

\(\begin{aligned} \frac{1}{N!}\sum _{x_{1}=1}^{L}\cdots \sum _{x_{N}=1}^{L}\det _{1\le j,m\le N}\left[ \varphi _{j}\left( x_{m}\right) \right] \det _{1\le l,n\le N}\left[ \phi _{l}\left( x_{n}\right) \right] =\det _{1\le j,l\le N}\left[ \sum _{x=1}^{L}\varphi _{j}\left( x\right) \phi _{l}\left( x\right) \right] . \end{aligned}\)
(25)

3.1 The Slater determinant representation of the Bethe wavefunction

By substituting Eq. (23) in the fundamental region into the Bethe wavefunction Eq. (22), we obtain,

\(\begin{aligned} \left| \Psi _{N+1,Q}\{k_{j,}\Lambda \}\right\rangle \propto \sum _{P\in S_{N+1}}\epsilon \left( P\right) e^{ik_{P0}x_{\downarrow }}\prod _{j=1}^{N}\frac{\exp \left[ ik_{Pj}x_{j}+i\delta _{Pj}\right] }{\sin \delta _{Pj}}, \end{aligned}\)
(26)

where we explicitly single out the plane-wave function for the impurity coordinate \(x_{\downarrow }\). Let us now introduce the single-particle wavefunction,

\(\begin{aligned} \chi _{j}\left( x\right) =\sqrt{\frac{1}{L}}\frac{\exp \left[ ik_{j}x+i\delta _{j}\right] }{\sin \delta _{j}}=\left[ \frac{\sin \left( k_{j}\right) -\Lambda -iu}{-u}\right] \sqrt{\frac{1}{L}}\exp \left[ ik_{j}x\right] . \end{aligned}\)
(27)

Therefore, the Bethe wavefunction \(\left| \Psi _{N+1,Q}(\{k_{j}\},\Lambda )\right\rangle\) takes the form of a \((N+1)\times (N+1)\) determinant,

\(\begin{aligned} \left| \Psi _{N+1,Q}(\{k_{j}\},\Lambda )\right\rangle =\frac{C_{\Psi }}{\sqrt{N!L}}\sum _{P\in S_{N+1}}\epsilon \left( P\right) e^{ik_{P0}x_{\downarrow }}\prod _{j=1}^{N}\chi _{Pj}\left( x_{j}\right) =\frac{C_{\Psi }}{\sqrt{N!L}}\left| \begin{array}{cccc} e^{ik_{1}x_{\downarrow }} & \chi _{1}\left( x_{1}\right) & \cdots & \chi _{1}\left( x_{N}\right) \\ \vdots & \ddots & \cdots & \vdots \\ \vdots & \vdots & \ddots & \vdots \\ e^{ik_{N+1}x_{\downarrow }} & \chi _{N+1}\left( x_{1}\right) & \cdots & \chi _{N+1}\left( x_{N}\right) \end{array}\right| , \end{aligned}\)
(28)

where \(C_{\Psi }\) is the normalization factor to be determined soon. As we work in the fundamental region \(R=\{x_{\downarrow }, it is useful to introduce new coordinates \(y_{j}=x_{j}-x_{\downarrow }\) relative to the impurity position and rewrite the wavefunction into the form,

\(\begin{aligned} \left| \Psi _{N+1,Q}(\{k_{j}\},\Lambda )\right\rangle & =\frac{C_{\Psi }}{\sqrt{N!}}\sqrt{\frac{1}{L}}e^{iQx_{\downarrow }}\left| \begin{array}{cccc} 1 & \chi _{1}\left( y_{1}\right) & \cdots & \chi _{1}\left( y_{N}\right) \\ \vdots & \ddots & \cdots & \vdots \\ \vdots & \vdots & \ddots & \vdots \\ 1 & \chi _{N+1}\left( y_{1}\right) & \cdots & \chi _{N+1}\left( y_{N}\right) \end{array}\right| ,\end{aligned}\)
(29)

\(\begin{aligned} & =\frac{C_{\Psi }}{\sqrt{N!}}\sqrt{\frac{1}{L}}e^{iQx_{\downarrow }}\left| \begin{array}{ccc} \chi _{1}\left( y_{1}\right) -\chi _{N+1}\left( y_{1}\right) & \cdots & \chi _{1}\left( y_{N}\right) -\chi _{N+1}\left( y_{N}\right) \\ \ddots & \cdots & \vdots \\ \chi _{N}\left( y_{1}\right) -\chi _{N+1}\left( y_{1}\right) & \ddots & \chi _{N}\left( y_{N}\right) -\chi _{N+1}\left( y_{N}\right) \end{array}\right| , \end{aligned}\)
(30)

where in the second expression, we have absorbed a trivial factor of \((-1)^{N}=-1\) into the normalization factor \(C_{\Psi }\). To further simplify the notation, let us introduce another single-particle wavefunction,

\(\begin{aligned} \phi _{j}\left( y\right) =\chi _{j}\left( y\right) -\chi _{N+1}\left( y\right) =\sqrt{\frac{1}{L}}\frac{\exp \left[ ik_{j}y+i\delta _{j}\right] }{\sin \delta _{j}}-\sqrt{\frac{1}{L}}\frac{\exp \left[ ik_{N+1}y+i\delta _{N+1}\right] }{\sin \delta _{N+1}}. \end{aligned}\)
(31)

We finally cast the Bethe wavefunction into the desired \(N\times N\) Slater determinant,

\(\begin{aligned} \left| \Psi _{N+1,Q}\{k_{j,}\Lambda \}\right\rangle =\frac{C_{\Psi }}{\sqrt{N!}}\sqrt{\frac{1}{L}}e^{iQx_{\downarrow }}\det _{1\le j,m\le N}\left[ \phi _{j}\left( y_{m}\right) \right] . \end{aligned}\)
(32)

3.2 The normalization factor of the Bethe wavefunction

The normalization factor \(C_{\Psi }\) can be easily determined by using the identity Eq. (25). By applying the normalization \(\left\langle \Psi _{N+1,Q}(\{k_{j}\},\Lambda )\mid \Psi _{N+1,Q}(\{k_{j}\},\Lambda )\right\rangle =1\), after completing the trivial summation on \(x_{\downarrow }\), it is straightforward to obtain

\(\begin{aligned} \left| C_{\Psi }\right| ^{-2}=\frac{1}{N!}\sum _{y_{1}=1}^{L}\cdots \sum _{y_{N}=1}^{L}\det _{1\le j,m\le N}\left[ \phi _{j}^{*}\left( y_{m}\right) \right] \det _{1\le l,n\le N}\left[ \phi _{l}\left( y_{n}\right) \right] =\det _{1\le j,l\le N}\left[ \sum _{y=1}^{L}\phi _{j}^{*}\left( y\right) \phi _{l}\left( y\right) \right] . \end{aligned}\)
(33)

To calculate the summation \(\sum _{y=1}^{L}\phi _{j}^{*}(y)\phi _{l}(y)\), let us first check

\(\begin{aligned} A_{jl}=\sum _{y=1}^{L}\bar{\chi }_{j}\left( y\right) \chi _{l}\left( y\right) , \end{aligned}\)
(34)

where \(j,l=1,\cdots ,N+1\) and

\(\begin{aligned} \bar{\chi }_{j}\left( y\right) \equiv \left[ \frac{\sin \left( k_{j}\right) -\Lambda +iu}{-u}\right] \sqrt{\frac{1}{L}}\exp \left[ -ik_{j}y\right] . \end{aligned}\)
(35)

Note that, for a real quasi-momentum \(k_{j}\), we trivially have \(\chi _{j}^{*}(y)=\bar{\chi }_{j}(y)\). We find that,

\(\begin{aligned} A_{jl}=\left[ \frac{\sin \left( k_{j}\right) -\Lambda +iu}{-u}\right] \left[ \frac{\sin \left( k_{l}\right) -\Lambda -iu}{-u}\right] \frac{1}{L}\sum _{y=1}^{L}\exp \left[ -i\left( k_{j}-k_{l}\right) y\right] . \end{aligned}\)
(36)

Let us consider the case with \(j\ne l\):

\(\begin{aligned} A_{jl} & = \left[ \frac{\sin \left( k_{j}\right) -\Lambda +iu}{-u}\right] \left[ \frac{\sin \left( k_{l}\right) -\Lambda -iu}{-u}\right] \frac{1}{L}\frac{e^{-i\left( k_{j}-k_{l}\right) }}{1-e^{-i\left( k_{j}-k_{l}\right) }}\left[ 1-e^{-i\left( k_{j}-k_{l}\right) L}\right] ,\end{aligned}\)
(37)

\(\begin{aligned} & = \frac{2i\left[ \sin \left( k_{l}\right) -\sin \left( k_{j}\right) \right] }{u}\frac{1}{L}\frac{1}{e^{i\left( k_{j}-k_{l}\right) }-1},\end{aligned}\)
(38)

\(\begin{aligned} & = -\frac{e^{-ik_{j}}+e^{ik_{l}}}{Lu}. \end{aligned}\)
(39)

Here, in the first step we have used the Bethe ansatz equation such as \(e^{ik_{j}L}=[\sin (k_{j})-\Lambda +iu]/[\sin (k_{j})-\Lambda -iu]\) and in the second step we have used the identity \(\left[ e^{i(k_{j}-k_{l})}-1\right] (e^{-ik_{j}}+e^{ik_{l}})=-2i[\sin (k_{l})-\sin (k_{j})]\). For the case with \(j=l\), we obtain

\(\begin{aligned} A_{jj}=\left[ \frac{\sin \left( k_{j}\right) -\Lambda +iu}{-u}\right] \left[ \frac{\sin \left( k_{j}\right) -\Lambda -iu}{-u}\right] =\frac{1}{\sin ^{2}\delta _{j}}, \end{aligned}\)
(40)

where the second expression in terms of \(\sin \delta _{j}\) is convenient for a real quasi-momentum \(k_{j}\).

For simplicity, let us now assume that all the quasi-momenta are real. The complex-valued pair of quasi-momenta can be easily treated in a moment. By using \(A_{jl}\), it is easy to see that (\(j,l=1,\cdots ,N\)),

\(\begin{aligned} \sum _{y=1}^{L}\phi _{j}^{*}\left( y\right) \phi _{l}\left( y\right) & = \sum _{y=1}^{L}\left[ \bar{\chi }_{j}\left( y\right) -\bar{\chi }_{N+1}\left( y\right) \right] \left[ \chi _{l}\left( y\right) -\chi _{N+1}\left( y\right) \right] ,\end{aligned}\)
(41)

\(\begin{aligned} & = A_{jl}+\frac{e^{-ik_{j}}+e^{ik_{N+1}}}{Lu}+\frac{e^{-ik_{N+1}}+e^{ik_{l}}}{Lu}+\frac{1}{\sin ^{2}\delta _{N+1}}. \end{aligned}\)
(42)

At this point, it is useful to define the variable

\(\begin{aligned} u_{j}=\frac{1}{\sin ^{2}\delta _{j}}+\frac{2\cos \left( k_{j}\right) }{Lu}=1+\frac{\left[ \sin \left( k_{j}\right) -\Lambda \right] ^{2}}{u^{2}}+\frac{2\cos \left( k_{j}\right) }{Lu}, \end{aligned}\)
(43)

where the second expression is more general and holds for a complex-valued quasi-momentum \(k_{j}\). Then, it is straightforward to obtain,

\(\begin{aligned} \sum _{y=1}^{L}\phi _{j}^{*}\left( y\right) \phi _{l}\left( y\right) =\left\{ \begin{array}{cc} u_{j}+u_{N+1} & \text {if}\ j=l\\ u_{N+1} & \text {if }j\ne l \end{array}\right. . \end{aligned}\)
(44)

The expression of the normalization factor \(C_{\Psi }\) becomes,

\(\begin{aligned} \left| C_{\Psi }\right| ^{-2}=\left| \begin{array}{cccc} u_{1}+u_{N+1} & u_{N+1} & \cdots & u_{N+1}\\ u_{N+1} & u_{2}+u_{N+1} & \cdots & u_{N+1}\\ \vdots & \vdots & \ddots & \vdots \\ u_{N+1} & u_{N+1} & \cdots & u_{N}+u_{N+1} \end{array}\right| =\left| \begin{array}{ccccc} u_{1} & -u_{2} & 0 & \cdots & 0\\ 0 & u_{2} & -u_{3} & \cdots & 0\\ \vdots & \ddots & \ddots & \cdots & \vdots \\ 0 & 0 & \cdots & u_{N-1} & -u_{N}\\ u_{N+1} & u_{N+1} & \cdots & u_{N+1} & u_{N}+u_{N+1} \end{array}\right| . \end{aligned}\)
(45)

This \(N\times N\) determinant is easy to calculate in a recursive way and we find that,

\(\begin{aligned} \left| C_{\Psi }\right| ^{-2}=u_{1}u_{2}\cdots u_{N+1}\left( \frac{1}{u_{1}}+\frac{1}{u_{2}}+\cdots +\frac{1}{u_{N+1}}\right) , \end{aligned}\)
(46)

which is a symmetric function of \(u_{1},u_{2},\cdots ,u_{N+1}\), as expected.

In the case of a (single) complex-valued pair of quasi-momenta, let us assume for concreteness that they are given by \(k_{1}=k_{R}+ik_{I}\) and \(k_{2}=k_{R}-ik_{I}\). We only need to take care of \(\chi _{1}^{*}(y)=\bar{\chi }_{2}(y)\) and \(\chi _{2}^{*}(y)=\bar{\chi }_{1}(y)\), i.e., the row index 1 and 2 are interchanged. As a result, we need to exchange the first row and second row of the previous \(N\times N\) determinant for \(\left| C_{\Psi }\right| ^{-2}\). This brings a minus sign for \(\left| C_{\Psi }\right| ^{-2}\). Let us denote the number of pairs of complex-valued quasi-momenta in the Bethe ansatz solution by an integer variable \(I_{B}\), although we only have one pair at most in our Fermi polaron problem. Then, we may write the general expression,

\(\begin{aligned} \left| C_{\Psi }\right| ^{-2}=\left( -1\right) ^{I_{B}}u_{1}u_{2}\cdots u_{N+1}\left( \frac{1}{u_{1}}+\frac{1}{u_{2}}+\cdots +\frac{1}{u_{N+1}}\right) , \end{aligned}\)
(47)

where \(I_{B}=0\) and \(I_{B}=1\) for the all real-k states and the \(k-\Lambda\) string states, respectively. We note that, in general, \(u_{j}\) could be complex-valued due to the bound-state and would be better calculated in terms of \(k_{j}\) in Eq. (43). We note also that, Eq. (47) is valid for \(N=1\). In this case, we have only one single-particle state \(\phi _{1}(y)=\chi _{1}(y)-\chi _{2}(y)\). For the complex-value pair, we then have \(\phi _{1}^{*}(y)=\chi _{1}^{*}(y)-\chi _{2}^{*}(y)=-[\bar{\chi }_{1}(y)-\bar{\chi }_{2}(y)]\). A minus sign automatically appears.

3.3 The form factor

We are now ready to derive the expression of the form factor. Let us slightly rewrite the product wavefunction in terms of the relative coordinates \(y_{m}\) (\(m=1,\cdots ,N\)),

\(\begin{aligned} \psi _{Q\downarrow }^{\dagger }\left| \text {FS}_{N}\right\rangle =\frac{1}{\sqrt{N!}}\sqrt{\frac{1}{L}}e^{iQx_{\downarrow }}\det _{1\le j,m\le N}\left( \sqrt{\frac{1}{L}}e^{iq_{j}y_{m}}\right) . \end{aligned}\)
(48)

The change of \(x_{m}\) to \(y_{m}\) is allowed, since \(\sum _{j}q_{j}x_{\downarrow }=0\). Therefore, by using the identity Eq. (25), the form factor \(F_{N+1}(\{k_{j}\},\Lambda )\) is given by

\(\begin{aligned} F_{N+1}\left( \{k_{j}\},\Lambda \right) & = \frac{C_{\Psi }}{N!}\sum _{y_{1}=1}^{L}\cdots \sum _{y_{N}=1}^{L}\det _{1\le j,m\le N}\left( \sqrt{\frac{1}{L}}e^{-iq_{j}y_{m}}\right) \det _{1\le l,n\le N}\left[ \phi _{l}\left( y_{n}\right) \right] ,\end{aligned}\)
(49)

\(\begin{aligned} & = C_{\Psi }\det _{1\le j,l\le N}\left[ \sqrt{\frac{1}{L}}\sum _{y=1}^{L}e^{-iq_{j}y}\phi _{l}\left( y\right) \right] . \end{aligned}\)
(50)

To complete the summation in the determinant, let us first check

\(\begin{aligned} B_{jl} & = \sqrt{\frac{1}{L}}\sum _{y=1}^{L}e^{-iq_{j}y}\chi _{l}\left( y\right) =\left[ \frac{\sin \left( k_{l}\right) -\Lambda -iu}{-u}\right] \frac{1}{L}\sum _{y=1}^{L}\exp \left[ -i\left( q_{j}-k_{l}\right) y\right] ,\end{aligned}\)
(51)

\(\begin{aligned} & = \left[ \frac{\sin \left( k_{l}\right) -\Lambda -iu}{-u}\right] \frac{1}{L}\frac{e^{-i\left( q_{j}-k_{l}\right) }}{1-e^{-i\left( q_{j}-k_{l}\right) }}\left[ 1-e^{-i\left( q_{j}-k_{l}\right) L}\right] . \end{aligned}\)
(52)

By using \(e^{-iq_{j}L}=1\) and \(e^{ik_{l}L}=[\sin (k_{l})-\Lambda +iu]/[\sin (k_{l})-\Lambda -iu]\), we find that,

\(\begin{aligned} B_{jl}=\frac{2i}{L}\frac{1}{e^{i\left( q_{j}-k_{l}\right) }-1}=\frac{1}{L}\frac{e^{-iq_{j}}+e^{ik_{l}}}{\sin \left( q_{j}\right) -\sin \left( k_{l}\right) }. \end{aligned}\)
(53)

Therefore, we obtain,

\(\begin{aligned} \sqrt{\frac{1}{L}}\sum _{y=1}^{L}e^{-iq_{j}y}\phi _{l}\left( y\right) =B_{jl}-B_{j,N+1}=\frac{1}{L}\frac{e^{-iq_{j}}+e^{ik_{l}}}{\sin \left( q_{j}\right) -\sin \left( k_{l}\right) }-\frac{1}{L}\frac{e^{-iq_{j}}+e^{ik_{N+1}}}{\sin \left( q_{j}\right) -\sin \left( k_{N+1}\right) }. \end{aligned}\)
(54)

Finally, we may write the form factor in terms of a \((N+1)\times (N+1)\) determinant,

\(\begin{aligned} F_{N+1}\left( \{k_{j}\},\Lambda \right) =C_{\Psi }\left| \begin{array}{cccc} B_{11} & \cdots & B_{1N} & B_{1,N+1}\\ \vdots & \vdots & \vdots & \vdots \\ B_{N1} & \cdots & B_{NN} & B_{N,N+1}\\ 1 & \cdots & 1 & 1 \end{array}\right| . \end{aligned}\)
(55)

4 The irregular many-body states

As we mentioned earlier, the regular Bethe wavefunctions with finite quasi-momenta \(\{k_{j}\}\) and \(\Lambda\) do not cover all the many-body states of the one-dimensional Hubbard model [46, 53]. We have other irregular quantum states, which contribute to the important sum rule Eq. (17). This is clearly seen in numerical calculations. While at zero or small total momentum, the sum of the residues of all the regular Bethe wavefunctions is exactly unity, at large total momentum (i.e., \(Q=\pi\)) the sum is less than 1, due to the exclusion of irregular quantum states that have significant residue.

4.1 A simple example with two-site Hubbard model

A simple example of irregular quantum states can be obtained by considering a two-site Hubbard model (\(L=2\)). As discussed in Ref. [53], in the \((1+1)\)-sector of one spin-up fermion and one spin-down fermion, we have the following two regular Bethe states with a total momentum \(Q=0\) and the quasi-momentum \(\Lambda =0\), and with the energies \(D_{\mp }=[U/2\mp \sqrt{U^{2}/4+16t^{2}}]/t\),

\(\begin{aligned} \psi _{\downarrow \uparrow }\left( k_{1}^{-},k_{2}^{-}\right) & = \frac{1}{\sqrt{D_{-}^{2}/8+2}}\left[ -\frac{D_{-}}{4}\left| \psi _{1}\right\rangle +\left| \psi _{2}\right\rangle \right] ,\end{aligned}\)
(56)

\(\begin{aligned} \psi _{\downarrow \uparrow }\left( k_{1}^{+},k_{2}^{+}\right) & = \frac{1}{\sqrt{D_{+}^{2}/8+2}}\left[ -\frac{D_{+}}{4}\left| \psi _{1}\right\rangle +\left| \psi _{2}\right\rangle \right] , \end{aligned}\)
(57)

where

\(\begin{aligned} \left| \psi _{1}\right\rangle & = \left( \psi _{1\uparrow }^{\dagger }\psi _{1\downarrow }^{\dagger }+\psi _{2\uparrow }^{\dagger }\psi _{2\downarrow }^{\dagger }\right) \left| 0\right\rangle ,\end{aligned}\)
(58)

\(\begin{aligned} \left| \psi _{2}\right\rangle & = \left( \psi _{1\uparrow }^{\dagger }\psi _{2\downarrow }^{\dagger }-\psi _{1\downarrow }^{\dagger }\psi _{2\uparrow }^{\dagger }\right) \left| 0\right\rangle ,\end{aligned}\)
(59)

\(\begin{aligned} e^{ik_{1}^{\pm }} & = -\frac{D_{\pm }}{4}+\sqrt{\left( \frac{D_{\pm }}{4}\right) ^{2}-1}. \end{aligned}\)
(60)

The total residues of these two regular Bethe states are precisely unity at the total momentum \(Q=0\), as numerically confirmed.

As the dimension of the total Hilbert space in the \((1+1)\)-sector is 4 (i.e., the spin-up fermion and the spin-down fermion each can occupy two sites), we know that there are two other quantum states. It is readily seen that the two states are given by,

\(\begin{aligned} \left| \eta \right\rangle & = \frac{1}{\sqrt{2}}\left( \psi _{1\uparrow }^{\dagger }\psi _{1\downarrow }^{\dagger }-\psi _{2\uparrow }^{\dagger }\psi _{2\downarrow }^{\dagger }\right) \left| 0\right\rangle ,\end{aligned}\)
(61)

\(\begin{aligned} \left| \zeta \right\rangle & = \frac{1}{\sqrt{2}}\left( \psi _{1\uparrow }^{\dagger }\psi _{2\downarrow }^{\dagger }+\psi _{1\downarrow }^{\dagger }\psi _{2\uparrow }^{\dagger }\right) \left| 0\right\rangle , \end{aligned}\)
(62)

and have a total momentum \(Q=\pi =2\pi /L\). Both \(\left| \eta \right\rangle\) and \(\left| \zeta \right\rangle\) states are not described by the regular Bethe wavefunctions, i.e., in Eq. (8) we can not find finite quasi-momenta \(k_{1}\), \(k_{2}\) and \(\Lambda\), that can reproduce these two states. At the total momentum \(Q=\pi\), we find that the states \(\left| \eta \right\rangle\) and \(\left| \zeta \right\rangle\) have the form factor \(1/\sqrt{2}\) and \(-1/\sqrt{2}\), respectively, and they exhaust the sum rule Eq. (17).

4.2 The construction of irregular quantum states

Quite generally, it turns out that the irregular quantum states could be generated by acting the \(\zeta ^{\dagger }\) spin-flip operator and \(\eta ^{\dagger }\) pairing operator to some quantum states \(\left| \varphi \right\rangle\). These two operators are defined as follows,

\(\begin{aligned} \zeta & = \sum _{j=1}^{L}\psi _{j\uparrow }^{\dagger }\psi _{j\downarrow }=\sum _{k}\psi _{k\uparrow }^{\dagger }\psi _{k\downarrow },\end{aligned}\)
(63)

\(\begin{aligned} \eta & = \sum _{j=1}^{L}\left( -1\right) ^{j}\psi _{j\uparrow }\psi _{j\downarrow }=\sum _{k}\psi _{\pi -k\uparrow }\psi _{k\downarrow }. \end{aligned}\)
(64)

As both \(\zeta ^{\dagger }\) and \(\eta ^{\dagger }\) contain a creation operator for the impurity particle, it is easy to see that the quantum states \(\left| \varphi \right\rangle\) should be the non-interacting states consisting of either \(N+1\) or \(N-1\) spin-up fermions, which are very easy to construct (see below for the construction). Moreover, the states \(\zeta ^{\dagger }\left| \varphi \right\rangle\) and \(\left| \varphi \right\rangle\) have the same energy (i.e., \(E_{\varphi }\)), so the action of the spin-flip operator \(\zeta ^{\dagger }\) does not change the energy of the state. In contrast, the action of the \(\eta\)-pairing operator \(\eta ^{\dagger }\) will increase the energy by an amount U. To see this, let us recall the commutation relation [56],

\(\begin{aligned} \left[ \eta ^{\dagger },\mathcal {H}\right] =\eta ^{\dagger }\mathcal {H-H\eta ^{\dagger }=}-U\eta ^{\dagger }. \end{aligned}\)
(65)

It is readily seen that,

\(\begin{aligned} \mathcal {H}\eta ^{\dagger }\left| \varphi \right\rangle =\left( E_{\varphi }+U\right) \eta ^{\dagger }\left| \varphi \right\rangle , \end{aligned}\)
(66)

showing that the state \(\eta ^{\dagger }\left| \varphi \right\rangle\) is an exact eigenstate of the Hamiltonian that has an energy U more than the non-interacting state \(\left| \varphi \right\rangle\) [56].

We now wish to construct the irregular quantum states \(\zeta ^{\dagger }\left| \varphi \right\rangle\) and \(\eta ^{\dagger }\left| \varphi \right\rangle\) that have non-zero overlap with the initial product state,

\(\begin{aligned} \left| \Psi _{0}\right\rangle =\psi _{Q\downarrow }^{\dagger }\left| \text {FS}_{N}\right\rangle =\psi _{Q\downarrow }^{\dagger }\prod _{j=1}^{N}\psi _{q_{j}\uparrow }^{\dagger }\left| 0\right\rangle , \end{aligned}\)
(67)

where \(q_{j}\in [-(N-1)/2,\cdots ,-1,0,1,\cdots ,+(N-1)/2](2\pi /L)\). For this purpose, let us consider the states, \(\zeta \left| \Psi _{0}\right\rangle\) and \(\eta \left| \Psi _{0}\right\rangle\),

\(\begin{aligned} \zeta \left| \Psi _{0}\right\rangle & = \left( \sum _{k}\psi _{k\uparrow }^{\dagger }\psi _{k\downarrow }\right) \psi _{Q\downarrow }^{\dagger }\prod _{j=1}^{N}\psi _{q_{j}\uparrow }^{\dagger }\left| 0\right\rangle =\psi _{Q\uparrow }^{\dagger }\prod _{j=1}^{N}\psi _{q_{j}\uparrow }^{\dagger }\left| 0\right\rangle ,\end{aligned}\)
(68)

\(\begin{aligned} \eta \left| \Psi _{0}\right\rangle & = \left( \sum _{k}\psi _{\pi -k\uparrow }\psi _{k\downarrow }\right) \psi _{Q\downarrow }^{\dagger }\prod _{j=1}^{N}\psi _{q_{j}\uparrow }^{\dagger }\left| 0\right\rangle =\psi _{\pi -Q\uparrow }\prod _{j=1}^{N}\psi _{q_{j}\uparrow }^{\dagger }\left| 0\right\rangle . \end{aligned}\)
(69)

It is easy to see that the state \(\zeta \left| \Psi _{0}\right\rangle\) exists if \(Q\notin \{q_{j}\}\), and the state \(\eta \left| \Psi _{0}\right\rangle\) exists if \(\pi -Q\in \{q_{j}\}\). Let us discuss the two cases separately.

4.2.1 The \(\zeta\) spin-flip state

In the case that \(Q\notin \{q_{j}\}\), we may construct a \(\zeta\) spin-flip state,

\(\begin{aligned} \left| \Psi _{\zeta }\right\rangle & =C_{\zeta }\zeta ^{\dagger }\left[ \psi _{Q\uparrow }^{\dagger }\prod _{j=1}^{N}\psi _{q_{j}\uparrow }^{\dagger }\left| 0\right\rangle \right] ,\end{aligned}\)
(70)

\(\begin{aligned} & =\frac{\zeta ^{\dagger }}{\sqrt{N+1}}\left[ \psi _{Q\uparrow }^{\dagger }\prod _{j=1}^{N}\psi _{q_{j}\uparrow }^{\dagger }\left| 0\right\rangle \right] . \end{aligned}\)
(71)

Here, the normalization coefficient \(C_{\zeta }=1/\sqrt{N+1}\), since \(N+1\) orthogonal terms are created, when we act the spin-flip operator \(\zeta ^{\dagger }\) on \(\left| \varphi \right\rangle =\zeta \left| \Psi _{0}\right\rangle\). The energy of this \(\zeta\) spin-flip state is given by \(E_{0}=-2t\cos Q+E_{\text {FS},N}\), where \(E_{\text {FS},N}\) is the energy of the Fermi sea, as we defined earlier. Its overlap or the form factor with the initial state \(\left| \Psi _{0}\right\rangle\) is simply \(F_{\zeta }=C_{\zeta }=1/\sqrt{N+1}\).

4.2.2 The \(\eta\)-pairing state

In the case that \(\pi -Q\in \{q_{j}\}\), we may similarly construct an \(\eta\)-pairing state,

\(\begin{aligned} \left| \Psi _{\eta }\right\rangle & =C_{\eta }\eta ^{\dagger }\left[ \psi _{\pi -Q\uparrow }\prod _{j=1}^{N}\psi _{q_{j}\uparrow }^{\dagger }\left| 0\right\rangle \right] ,\end{aligned}\)
(72)

\(\begin{aligned} & =\frac{\eta ^{\dagger }}{\sqrt{L-N+1}}\left[ \psi _{\pi -Q\uparrow }\prod _{j=1}^{N}\psi _{q_{j}\uparrow }^{\dagger }\left| 0\right\rangle \right] . \end{aligned}\)
(73)

The normalization coefficient \(C_{\eta }=1/\sqrt{L-N+1}\), because \(L-N+1\) orthogonal terms are generated, when we act the \(\eta\)-pairing operator \(\eta ^{\dagger }\) on \(\left| \varphi \right\rangle =\eta \left| \Psi _{0}\right\rangle\). It is easy to see that the energy of the state \(\eta \left| \Psi _{0}\right\rangle\) is also \(E_{0}=-2t\cos Q+E_{\text {FS},N}\), since in this state we remove from the Fermi sea a single-particle state with momentum \(\pi -Q\) with energy \(-2t\cos (\pi -Q)=2t\cos Q\). Therefore, the energy of the \(\eta\)-paring state \(\left| \Psi _{\eta }\right\rangle\) is \(E_{0}+U\). Its overlap or the form factor with the initial state \(\left| \Psi _{0}\right\rangle\) is given by \(F_{\eta }=C_{\eta }=1/\sqrt{L-N+1}\).

4.3 The sum-rule

We can now work out the sum-rule for the sum \(\varrho _{\text {BA}}\) of the residues of all the regular Bethe wavefunctions and compare \(\varrho _{\text {BA}}\) with the sum of all the residues (i.e., \(\varrho _{s}=1\)). Let us define the Fermi wavevector \(k_{F}=N(2\pi /L)\), \(k_{c1}=\min \{k_{F},\pi -k_{F}\}\) and \(k_{c2}=\max \{k_{F},\pi -k_{F}\}\). For the momentum \(Q\in [0,\pi ]\), we find that,

\(\begin{aligned} \varrho _{\text {BA}}= \left\{ \begin{array}{c} 1,\\ 1-F_{\zeta }^{2},\\ 1-F_{\zeta }^{2}-F_{\eta }^{2}, \end{array}\quad \begin{array}{c} Q
(74)

As the special cases, \(\varrho _{\text {BA}}=1\) at \(Q=0\) and \(\varrho _{\text {BA}}=1-(L+2)/[(N+1)(L-N+1)]\) at \(Q=\pi\). In the thermodynamic limit (\(N\rightarrow \infty\) and \(L\rightarrow \infty\)), we always have \(\varrho _{\text {BA}}\rightarrow \varrho _{s}=1\), as expected.

For later convenience, we define the sum of the residues from the irregular quantum states as \(\varrho _{\text {irr}}\), which is \(\varrho _{\text {irr}}=F_{\zeta }^{2}=1/(N+1)\) when \(k_{c1} and is \(\varrho _{\text {irr}}=F_{\zeta }^{2}+F_{\eta }^{2}=1/(N+1)+1/(L-N+1)\) when \(k_{c2}. We also denote the sums of the residues from the all real-k solutions (including the spin-flip state) and from the \(k-\Lambda\) string solutions (including the \(\eta\)-pairing state) as \(\varrho _{k}\) and \(\varrho _{\Lambda }\), respectively. Therefore, \(\varrho _{k}+\varrho _{\Lambda }=1\).


5 Numerical calculations

For a given many-body state with a set of quasi-momenta \(\{k_{j}\}\) and \(\Lambda\), the calculation of its form factor in Eq. (55) is straightforward. We first calculate \(u_{j}\) in Eq. (43) by using \(k_{j}\) and determine the normalization factor of \(C_{\Psi }\) in Eq. (47). We then calculate the \((N+1)\times (N+1)\) determinant in Eq. (55) to obtain the form factor. We need to pay special attention for the \(k-\Lambda\) string solutions with a pair of complex-valued quasi-momenta, particularly for the normalization factor \(C_{\Psi }\). For convenience, we always consider the case that the lattice size L is an even integer.

5.1 The numerical solution of the Bethe ansatz equations

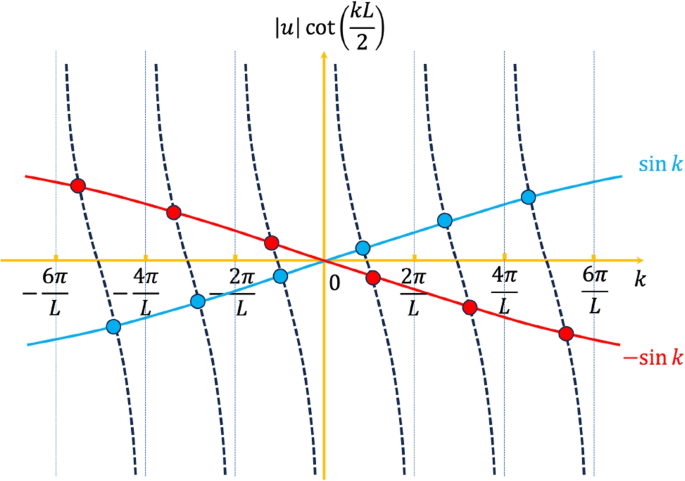
From Fig. 1, we find that each quasi-momentum \(k_{j}\) is uniquely characterized by an integer \(s_{j}\) in the region \((s_{j}-1)2\pi /L\le k_{j}. As we restrict the quasi-momentum in the first Brillouin zone \(k\in (-\pi ,+\pi ]\), the allowed values for \(s_{j}\) range from \(-L/2+1\) to L/2. For the solution with all real momenta \(\{k_{j}\}\), we simply assign the different integers \(\{s_{j}\}\) (\(j=1,\cdots ,N+1\)) and the integer \(n=Q/(2\pi /L)\), as a set of good quantum numbers to characterize the regular Bethe ansatz solution. We note that, in the standard textbook the quasi-momentum \(k_{j}\) is often specified by a half integer \(I_{j}\) for an odd number of particles N [46, 47, 57]. Our integer quantum number \(s_{j}\) is related to \(I_{j}\) by \(s_{j}=I_{j}+1/2\).

Numerically, for a selected quasi-momentum \(\Lambda \in (-\infty ,+\infty )\), we can solve Eq. (8) for \(\{k_{j}\}\), once a set of integers \(\{s_{j}\}\) is specified. We then obtain the total momentum \(Q=\sum _{j=1}^{N+1}k_{j}=n(2\pi /L)\). As we shall see below for the cases of \(U<0\) and \(U>0\) separately, there is one-to-one correspondence between the quasi-momentum \(\Lambda\) and the total momentum Q. Therefore, we can adjust the value of the quasi-momentum \(\Lambda\) to reach the given total momentum Q (or the specified quantum number n).

It is worth noting that, for the case of the \(k-\Lambda\) string solution (i.e., the bound-state), we need to solve Eq. (8) for the complex-valued quasi-momenta \(k_{1}=q+i\xi\) and \(k_{2}=q-i\xi\), with \(\xi >0\). In addition, we need to specify \(N-1\) integers \(\{s_{j}\}\) (\(j=3,\cdots ,N+1\)) for the real-valued quasi-momenta \(\{k_{j}\}\). After some simple algebra, we find that the complex-valued quasi-momenta satisfy the coupled equations (for a given \(\Lambda\)),

\(\begin{aligned} \sin \left( q\right) \cosh \left( \xi \right) & = \Lambda +u\frac{\sin \left( qL\right) }{\cosh \left( \xi L\right) -\cos \left( qL\right) }\equiv \tilde{\Lambda },\end{aligned}\)
(75)

\(\begin{aligned} \cos \left( q\right) \sinh \left( \xi \right) & = -u\frac{\sinh \left( \xi L\right) }{\cosh \left( \xi L\right) -\cos \left( qL\right) }\equiv -\tilde{u}. \end{aligned}\)
(76)

For sufficiently large lattice size \(L\gg 1\), we may approximate \(\tilde{\Lambda }\simeq \Lambda\) and \(\tilde{u}\simeq u\) and then solve the coupled equations for q and \(\xi\). This approximation gives a leading-order solution for the values of q and \(\xi\). Numerically, we then improve \(\tilde{\Lambda }\) and \(\tilde{\xi }\), and iteratively solve the coupled equations until the convergence is reached. In the limit \(\Lambda \rightarrow \pm \infty\), we find that \(q\rightarrow \pm \pi /2\) if \(u<0\) or \(q\rightarrow \mp \pi /2\) if \(u>0\).

5.1.1 Attractive on-site interaction \(U<0\)

It is straightforward to see that, for the solution with all real quasi-momenta \(\{k_{j}\}\),

\(\begin{aligned} Q\left( \Lambda \rightarrow -\infty \right) & = \frac{2\pi }{L}\sum _{j=1}^{N+1}s_{j},\end{aligned}\)
(77)

\(\begin{aligned} Q\left( \Lambda \rightarrow +\infty \right) & = \frac{2\pi }{L}\left[ \sum _{j=1}^{N+1}s_{j}-\left( N+1\right) \right] . \end{aligned}\)
(78)

Therefore, for a given total momentum \(Q=n(2\pi /L)\), where \(-L/2, by tuning \(\Lambda\) at most we can only find one value of \(\Lambda\) that makes \(Q=n(2\pi /L)\). For the \(k-\Lambda\) string solution, we find that,

\(\begin{aligned} Q\left( \Lambda \rightarrow -\infty \right) & = \frac{2\pi }{L}\left[ -\frac{L}{2}+\sum _{j=3}^{N+1}s_{j}\right] ,\end{aligned}\)
(79)

\(\begin{aligned} Q\left( \Lambda \rightarrow +\infty \right) & = \frac{2\pi }{L}\left[ +\frac{L}{2}+\sum _{j=3}^{N+1}s_{j}-\left( N-1\right) \right] . \end{aligned}\)
(80)

It is easy to see that, similarly at most we can only find one value of \(\Lambda\) that makes \(Q=n(2\pi /L)\).

5.1.2 Repulsive on-site interaction \(U>0\)

For a repulsive on-site interaction, the situation is similar, although the limiting values of the total momentum are reversed. However, one needs to take care of the \(k-\Lambda\) string solution. In this case, by changing \(\Lambda\) the value of q has a jump at \(\Lambda =0\), if we restrict \(q\in (-\pi ,\pi ]\). This unwanted jump can be readily removed, if we add \(2\pi\) to q when \(\Lambda <0\) or \(q<0\).

5.2 The set of quantum numbers \(\{s_{j}\}\)

For large L and N, the number of the regular Bethe wavefunctions is exponentially large. We need to pick up the Bethe wavefunctions with significant residue. A useful strategy is to classify the set of integers \(\{s_{j}\}\), according to the number of pseudo particle-hole excitations, created by modifying a pseudo Fermi sea configuration, which always exists.

This pseudo Fermi sea configuration is given by the set \(\{s_{j}\}=[-(N+1)/2+1,\cdots ,-1,0,1,\cdots ,(N+1)/2]\), which characterize the ground state for repulsive on-site interactions and a broken-pair state for attractive on-site interactions (see, i.e., Fig. 2b). We refer to an integer \(s_{H}\) in this pseudo Fermi sea set as a hole, and an integer \(s_{P}\) out of this set as a particle. More explicitly, we have \(s_{H}\in [-(N+1)/2+1,\cdots ,-1,0,1,\cdots ,(N+1)/2]\) and \(s_{P}\in [-L/2+1,\cdots ,-(N+1)/2]\cup [(N+1)/2+1,\cdots ,L/2]\). In general, for the set \(\{s_{j}\}\) named as n-particle-hole excitations, we pick up n particle values from \(\{s_{P}\}\) and fill them into (i.e., replace) the n hole values of \(\{s_{H}\}\). This idea applies to the \(k-\Lambda\) string solution as well. A slight modification is that we need to discard two particle values in the \(\{s_{j}\}\) set, to accommodate the pair of complex-valued quasi-momenta \(k_{1}\) and \(k_{2}=k_{1}^{*}\).

Fig. 2
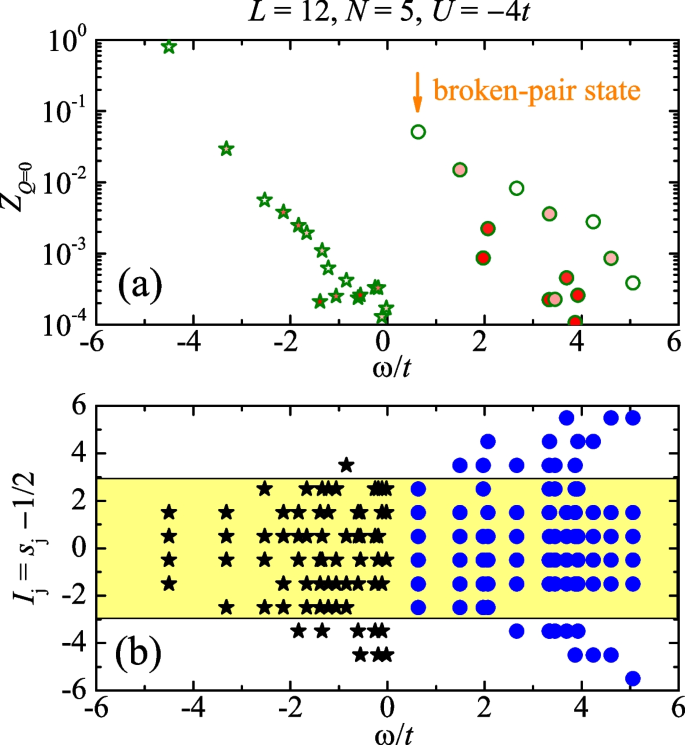
figure 2

Upper panel: Residues of different (i.e., n-th) Bethe wavefunctions at zero total momentum (\(Q=0\)) as a function of the energy \(\omega =E_{N+1}^{(n)}\left( \{k_{j}\},\Lambda \right) -E_{\text {FS},N}\) at the quarter filling \(\nu =(N+1)/L=0.5\) and at the attraction \(U=-4t\). We choose a small lattice size, i.e., \(L=12\) and \(N=5\), so the different many-body states can be well separated, for a better illustration. The stars and circles correspond to the \(k-\Lambda\) solutions and the all real-k solutions, respectively. The color of the symbols shows the value of the quasi-momentum \(\Lambda\), which increases as the color changes from blue to red. At zero momentum, all the states are doubly degenerate, so we only include the states with \(\Lambda \ge 0\). The arrow emphasizes the broken-pair state, discovered by McGuire with the Gaudin-Yang model [41]. Lower panel: Configurations of the quantum numbers \(\{I_{j}\}\) for different Bethe wavefunctions. The yellow area highlights the pseudo Fermi sea of the broken-pair state


In our numerical calculations, we have tried to include the Bethe wavefunctions with up to three pseudo particle-hole excitations, where the sum-rule \(\varrho _{s}=1\) is well satisfied. To have a large lattice size and particle number, however, we often truncate to the level of two pseudo particle-hole excitations. For example, at \(L=100\) and \(N=49\) and at the total momentum \(Q=\pi\), we find that the numbers of regular Bethe wavefunctions with one and two pseudo particle-hole excitations are 2161 and 1182934, respectively. The inclusion of these over-million quantum states leads to \(\varrho _{s}>0.996\) at \(U=4t\), i.e., the sum-rule is satisfied within \(0.4\%\) error.

6 Results and discussions

In the previous short Letter [48], we discussed the spectral properties of the impurity particle at repulsive on-site interactions. In this work, we would like to focus on attractive on-site interactions. Due to the particle-hole transformation as discussed in Section 2.3, which transforms the interaction strength from \(+U\) to \(-U\), these two situations have no difference in principle. However, the consideration of an attractive on-site interaction seems to be favorable to understand the polaron physics in one dimension. For example, it is well-known that with attractive interactions, the impurity naturally has two branches in its spectrum: a low-lying attractive Fermi polaron (or Fermi singularity) and a high-lying excited repulsive Fermi polaron (or Fermi singularity) [6, 9, 38,39,40]. Therefore, it would be interesting to see how the two branches emerge from the exact Bethe ansatz solution.

Without loss of generality, we will primarily take a lattice size \(L=40\) and a filling factor \(\nu =(N+1)/L=0.5\) (i.e., \(N=19\)), with the inclusion of two pseudo particle-hole excitations. The sum rule is satisfied at the level \(\varrho _{s}>0.998\), so we believe that the numerical convergence in choosing many-body states is well achieved. The consideration of a relative small number of spin-up fermions N follows the realistic experimental realization with ultracold atoms. We note that, strictly speaking, in the thermodynamic limit the impurity in one dimension might not behave like a polaron quasiparticle and the impurity spectral function would be dominated by Fermi singularities [43, 48]. However, experimentally, the characteristic of Fermi singularities may hardly be identified, due to the small number of particles in the Fermi bath.

6.1 The configuration of Bethe wavefunctions

Let us first discuss the configuration of different regular Bethe wavefunctions, by considering a small lattice size \(L=12\) and a small particle number \(N=5\) at an interaction strength \(U=-4t\). Under these parameters, the Bethe states are well separated in energy. In Fig. 2, we present the set of quantum numbers \(\{I_{j}=s_{j}-1/2\}\) of different Bethe states at zero total momentum (b) and the corresponding form factors (a).

At zero momentum \(Q=0\), all the Bethe states are doubly degenerate, except some states with \(\Lambda =0\) including the absolute ground state. This degeneracy can be easily understood from the Bethe ansatz Eq. (8), i.e., the equation holds when we change the sign of \(\{k_{j}\}\) and \(\Lambda\): \(k_{j}\rightarrow -k_{j}\) and \(\Lambda \rightarrow -\Lambda\). As the constraint \(Q=0=\sum _{j}k_{j}\) is not affected by this reverse operation, we would find two degenerate states, with quasi-momentum \(\Lambda \ne 0\) and \(-\Lambda\). In general, the double degeneracy is lost once the total momentum Q becomes nonzero. An exception is the case with the total momentum \(Q=\pi\). As the momentum \(\pi\) is related to the momentum \(-\pi\) by the reciprocal lattice momentum \(2\pi\), the constraint on the total momentum \(Q=\pi =\sum _{j}k_{j}\) is again not affected by the reverse operation \(k_{j}\rightarrow -k_{j}\). Therefore, the double degeneracy is recovered at the total momentum \(Q=\pi\). As a result of the double degeneracy at \(Q=0\), for clarity in Fig. 2b we show only the configuration \(\{I_{j}\}\) of the states with the quasi-momentum \(\Lambda \ge 0\). The configuration of the degenerate state is simply given by the set \(\{\tilde{I}_{j}=-I_{j}\}\).

From their configurations as a function of energy, we find that the all real-k states and the \(k-\Lambda\) string states are roughly separated by the on-site attraction \(U=-4t\). For the attractive on-site interaction, the all real-k state with the lowest energy, known as the broken-pair state [41], has the configuration of a pseudo Fermi sea. Typically, the states with a large energy has large particle numbers \(\left| s_{j,P}\right|\) or \(\left| I_{j,P}\right|\) out of the pseudo Fermi sea.

The separation of the two kinds (or branches) of states can also been clearly seen from the form factor shown in Fig. 2a. In each branch, the form factor generally decreases with increasing energy. In the lower branch of the \(k-\Lambda\) string states, the absolute ground state has the largest residue, which is almost unity. In the upper branch of the all real-k states, the broken-pair has the largest residue. However, the magnitude of its residue is significantly smaller.

6.2 The form factor and spectral function

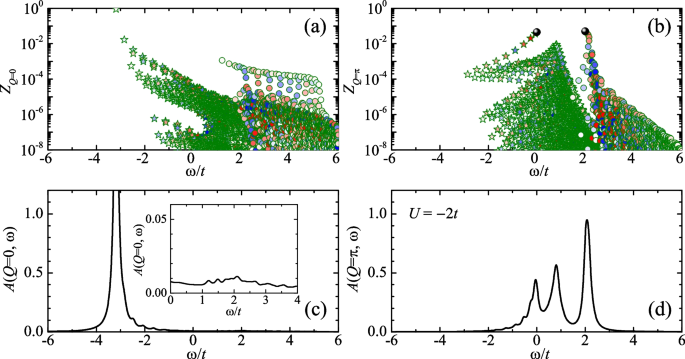
In Fig. 3, we report the form factors (upper panels) and spectral functions (lower panels) of a realistic situation with \(L=40\) and \(N=19\) at the on-site attraction \(U=-2t\). At zero total momentum \(Q=0\), as given in Fig. 3a, the form factor shows a similar characteristic as in Fig. 2a. The large residue of the absolute ground state leads to a sharp peak at the ground state energy \(\omega =E_{N+1}^{(0)}\left( \{k_{j}\},\Lambda \right) -E_{\text {FS},N}\sim -3t\) (see, i.e., Fig. 3c), where the superscript “0” indicates the ground state. At the small number of particles \(N=19\), we may treat this peak as a polaron quasiparticle, as the contribution from the nearby discrete excited states is negligible. For example, the first excited state has a residue at about 0.01, so the sharp peak is essentially contributed by the ground state only. By increasing L and N, the situation will be different, since the nearby excited states will become densely distributed and their residues will eventually render the sharp peak into a Fermi singularity [43, 48]. We note that, at the weak attraction \(U=-2t\), we can hardly identify the existence of the high-energy branch contributed from the all real-k states. At the energy of the broken-pair state, i.e., \(\omega \sim t\), we can only see a small, very broad background distribution, as highlighted in the inset of Fig. 3c, whose magnitude is consistent with the residue of the broken-pair state (i.e., \(Z\sim 0.001\)).

Fig. 3
figure 3

Residues (a and b) and the impurity spectral functions (c and d, in units of \(t^{-1}\)) as a function of the energy \(\omega =E_{N+1}^{(n)}\left( \{k_{j}\},\Lambda \right) -E_{\text {FS},N}\) at the quarter filling \(\nu =(N+1)/L=0.5\) and at the attraction \(U=-2t\). In the left and right columns, we show the results at zero momentum \(Q=0\) and at the momentum \(Q=\pi\), respectively. Here, we choose \(L=40\) and \(N=19\). As in Fig. 2, in the upper panels, the residues of the real-k solutions and the \(k-\Lambda\) solutions are shown by circles and stars, respectively, with the color of symbols indicating the value of the quasi-momentum \(\Lambda\). The two black dots in (b) show the residues of the spin-flip state (i.e., the right dot) and of the \(\eta\)-pairing state (the left dot). The inset in (c) highlights the repulsive branch of the spectral function starting at \(\omega \sim t\), contributed by all the real-k solutions


At the total momentum \(Q=\pi\), as shown in Fig. 3b, we find the behavior of the form factors as a function of the energy becomes very different. At this sector, compared with the \(Q=0\) case, we find three distinct features. First, the lowest energy state still locates at a similar energy \(\omega \sim -3t\). However, its residue \(Z\sim 10^{-4}\) becomes significantly smaller. By increasing energy, we find a series of the \(k-\Lambda\) string states whose residue rapidly increases. This series stops at the \(\eta\)-pairing state \(\left| \eta \right\rangle\) (see the left black dots in Fig. 3b), which precisely locates at the energy \(\omega _{\eta }=-2t\cos Q+U=0\). Second, at a bit higher energy \(\omega \sim t\), we find a cluster of the \(k-\Lambda\) string states, whose residues are notable (i.e., \(Z\sim 0.01\)). The number of states in the cluster is not small. Finally, we can also see clearly a series of the all real-k states, connecting smoothly to the spin-flip state \(\left| \xi \right\rangle\) at the energy \(\omega _{\xi }=-2t\cos Q=2t\), which is indicated by the right black dot in Fig. 3b. Remarkably, the three features in the form factors yield three peaks in the spectral function, as illustrated in Fig. 3d. It is worth emphasizing that the middle peak II, contributed by the cluster of the \(k-\Lambda\) string states, would be a true polaron quasiparticle, which will survive in the thermodynamic limit [48]. In contrast, the first peak (located near \(\omega _{\eta }=0\)) and the third peak (located near \(\omega _{\xi }=2t\)) will eventually turn into Fermi singularities with increasing L and N [48]. This coexistence of the Fermi singularities and the polaron quasiparticle in the thermodynamic limit could be a unique feature of Fermi polarons in one dimension.

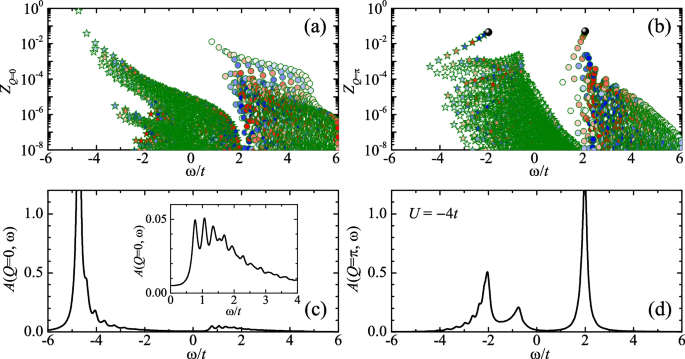
In Fig. 4, we present the results for the form factors and spectral functions at a larger attractive interaction, \(U=-4t\). By increasing attraction, at the total momentum \(Q=0\), we find that the high-lying repulsive branch in the spectral function become more significant (see the inset of Fig. 4c). At the total momentum \(Q=\pi\), the three features in the form factors become more pronounced and well separated. Moreover, in the spectral function the amplitude of the middle polaron peak II becomes smaller. We have tried other values of on-site attractive interaction strengths and find that the polaron peak II will completely disappear at sufficiently large attractions.

Fig. 4
figure 4

The same plots as in Fig. 3, except that the attractive interaction strength becomes \(U=-4t\). Due to the enhanced attraction, the repulsive branch of Fermi polarons at zero momentum \(Q=0\) becomes more significant, as highlighted in the inset of (c)


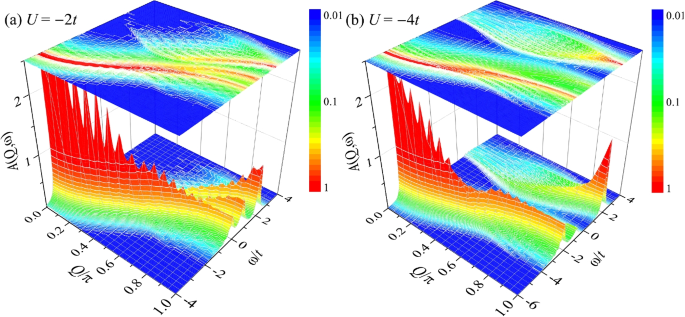
In closing this subsection, let us discuss the total momentum Q-dependence of the spectral function. As reported in Fig. 5, we show the three-dimensional plots of the spectral function at the two on-site attractions, \(U=-2t\) (a) and \(U=-4t\) (b). The projected two-dimensional contour plots are given at the top of the figures. By increasing the total momentum Q, the low-lying branch contributed from the \(k-\Lambda\) string states and the high-lying branch from the all real-k states give rise to the well-known lower and upper Hubbard bands, respectively. These two bands are clearly visible at the attraction \(U=-4t\). At a smaller attraction \(U=-2t\), we also see an additional middle band split from the lower Hubbard band, responsible for the middle polaron quasiparticle peak that we emphasized in Fig. 3d. This middle band also exists at \(U=-4t\) at the total momentum \(Q\sim \pi\). However, it becomes very shallow and eventually disappear at large attractions.

Fig. 5
figure 5

Three-dimensional plots of the spectral function \(A(Q,\omega )\), in units of \(t^{-1}\) as indicated by the color map, at the interaction strengths \(U=-2t\) (a) and \(U=-4t\) (b). The corresponding two-dimensional contour plots are also shown at the top of the figure. Here, we take the lattice size \(L=40\) and the number of spin-up fermions \(N=19\)


6.3 The dependence on the filling factor

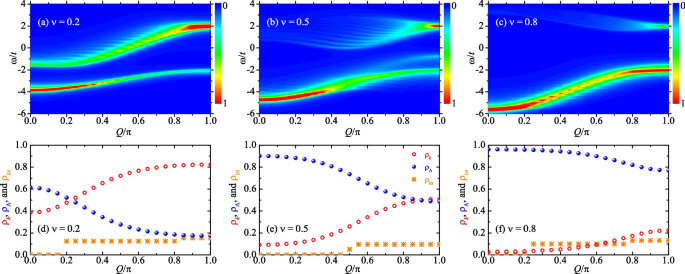
Let us finally consider the filling factor \(\nu\)-dependence of the impurity spectral function. In Fig. 6, we report the two-dimensional contour plots of the spectral function at three filling factors \(\nu =0.2\) (a), \(\nu =0.5\) (b) and \(\nu =0.8\) (c), and at the on-site attraction \(U=-4t\). The corresponding sums of the residues \(\varrho _{\Lambda }\), \(\varrho _{k}\) and \(\varrho _{\text {irr}}\), contributed from different quantum states are provided in the lower panels of the figure.

Fig. 6
figure 6

Upper panels: two-dimensional contour plots of the spectral function \(A(Q,\omega )\), in units of \(t^{-1}\) as indicated by the color map, at various filling factors \(\nu =0.2\) (a), \(\nu =0.5\) (b) and \(\nu =0.8\) (c). Lower panels (d, e, f): the corresponding sum of residues, contributed by the all real-k solutions and the spin-flip state (red open circles, \(\varrho _{k}\)), by the \(k-\Lambda\) string solutions and the \(\eta\)-pairing state (blue solid circles, \(\varrho _{\Lambda }\)). Note that, \(\varrho _{k}+\varrho _{\Lambda }=1\) following the sum rule. We also show the sum of the residues of the irregular spin-flip and \(\eta\)-pairing states as \(\varrho _{\text {irr}}\) (orange stars). Here, we consider the interaction strength \(U=-4t\), the lattice size \(L=40\), and the number of spin-up fermions \(N=\nu L-1\)


We find that \(\varrho _{\Lambda }\) and \(\varrho _{k}\) provide a useful measure of the relative strength of the low-lying and high-lying Hubbard bands, as a function of the total momentum Q. By increasing Q, the spectral weight of the low-lying Hubbard band (i.e., \(\varrho _{\Lambda }\)) decreases and the spectral weight of the high-lying Hubbard band (i.e., \(\varrho _{k}\)) increases. At the zero momentum (\(Q=0\)), the low-lying Hubbard band typically has more spectral weight than the high-lying band. At the total momentum \(Q=\pi\), we find that the values of \(\varrho _{\Lambda }\) and \(\varrho _{k}\) can be well approximated by \(\nu\) and \(1-\nu\), respectively.

7 Conclusions and outlooks

In conclusions, we have derived an analytic expression of the form factor for an impurity moving in a non-interacting Fermi bath, based on the exactly solvable one-dimensional Hubbard model. This analytic expression allows us to exactly calculate the spectral function of Fermi polarons in one-dimensional optical lattices with lattice sizes \(L\sim 100\) and to address the finite-size effect in the spectral properties by varying the lattice size. The same expression of the form factor could also be used to investigate the non-trivial quantum dynamics of the impurity, such as quantum flutter in optical lattices [49,50,51].

The current derivation of the form factor strongly relies on the fact that the many-body Bethe wavefunctions can be rewritten into a Slater determinant. A similar technique might be used to solve the problem of an impurity moving in an interacting Bose gas in one dimension, which is described by the bosonic Gaudin-Yang model with extreme spin-population imbalance [58]. This would provide us some exact results to better understand the spectral properties of one-dimensional Bose polarons.

In future studies, it would also be interesting to consider multiple fermionic impurities interacting with the one-dimensional Fermi bath. The finite number or finite density of impurities will introduce a pseudo Fermi sea of spinons for the spin degree of freedom [47]. As a result, we should be able to see spinon excitations in the spectral properties and the appearance of the intriguing spin-charge separation in the single-particle spectral function [57].