Dark states are a fundamental concept in quantum physics [1]. Light-matter interactions may lead to multiple pathways of transitions between atomic levels. Under appropriate conditions, destructive interference arises such that the atom cannot absorb or emit light and occupy certain states and. This textbook result has profound applications in a broad spectrum of topics, ranging from electromagnetically induced transparency and the storage of quantum information to the preparation of novel quantum states [2,3,4,5]. It is worth pointing out that flat bands in condensed matter arise from the same mechanism. In certain lattice models, localized orbitals become the eigenstates due to destructive interference between multiple tunneling processes, which leads to vanishing probabilities of occupying lattice sites other than those in the localized orbitals. Prototypical examples include Lieb lattice, sawtooth lattice, and Crutz lattice, to name a few [6,7,8,9,10].

To establish a dark state, there are certain strict requirements for the quantum system. For instance, in the \(\Lambda\) system, the most fundamental example of quantum systems supporting dark states, the two light fields coupling the first two states, which are denoted by \(|\uparrow \rangle\) and \(|\downarrow \rangle\) in Fig. 1, with the third one \(|3\rangle\) must be at resonance with the corresponding transitions. In other words, in the rotating frame, \(|\uparrow \rangle\) and \(|\downarrow \rangle\) need to be degenerate. If a perturbation breaks the degeneracy, for instance, an energy difference between \(|\uparrow \rangle\) and \(|\downarrow \rangle\), the destructive interference is suppressed and the dark state disappears. An important question thus arises: how to re-establish the dark state in the presence of perturbations?

In this work, we show that non-Hermitian couplings, such as losses and gains, can be introduced to the Hamiltonian as an efficient protocol to restore the dark state. This method can be applied to the \(\Lambda\) system in the presence of the most generic perturbations. Any undesired couplings between \(|\uparrow \rangle\) and \(|\downarrow \rangle\) can be compensated by the corresponding non-Hermitian terms. As such, the dark state interacts with the rest of the system only by unidirectional couplings and thus remains stable. This framework can also be used in a many-body system to overcome perturbations that destroy flat bands. Whereas there have been considerable efforts to study non-Hermitian flat bands in the literature [11,12,13,14,15,16,17], here, the generic principle of restoring dark states provides us with a systematic means to retain flat bands. For instance, undesired couplings in a Raman lattice [18], which is equivalent to coupled Su-Schrieffer-Heeger chains [19], lead to finite dispersion of the energy bands. Adding losses and gains reinstates the flat bands by creating localized orbitals that unidirectionally couple to other lattice sites. These localized orbitals span a few lattice sites such that on-site interactions are sufficient to induce charge-density waves and other novel many-body phases in non-Hermitian systems.

A \(\Lambda\) system is described by a Hamiltonian,

\(\begin{aligned} H_0=\Omega _1|\uparrow \rangle \langle 3|-\Omega _2|\downarrow \rangle \langle 3|+h.c. \end{aligned}\)
(1)

Since the phase of the couplings can be gauged away, we have chosen real \(\Omega _{1,2}\) to simplify notations. \(\hbar =1\) has been chosen in this manuscript. The dark state is written as

\(\begin{aligned} |D\rangle =\cos (\theta /2)|\uparrow \rangle +\sin (\theta /2)|\downarrow \rangle , \end{aligned}\)
(2)

where \(\cos (\theta /2)=\Omega _2/\Omega\), \(\sin (\theta /2)=\Omega _1/\Omega\), and \(\Omega =\sqrt{\Omega _1^2+\Omega _2^2}\). As shown by Fig. 1A, \(|D\rangle\) is denoted by a vector on the Bloch sphere. Using \(|D\rangle\) and the orthogonal \(|B\rangle =-\sin (\theta /2)|\uparrow \rangle +\cos (\theta /2)|\downarrow \rangle\), the Hamiltonian is rewritten as

\(\begin{aligned} H_0=\Omega |B\rangle \langle 3|+h.c. \end{aligned}\)
(3)

Fig. 1
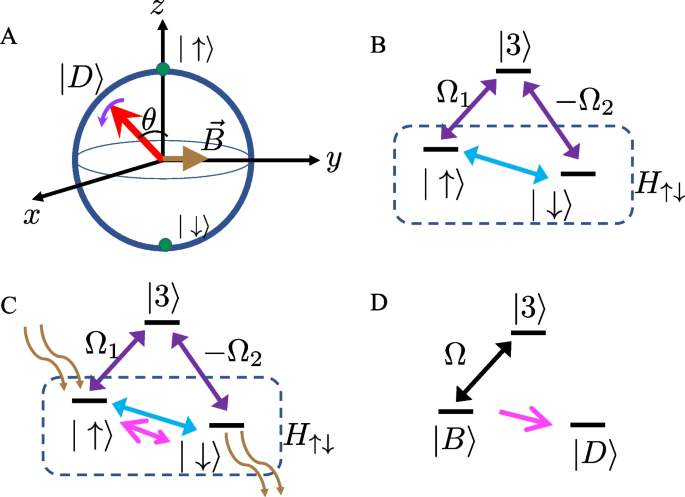
figure 1

A A dark state is represented by a red vector oriented along a certain direction on the Bloch sphere. \(\theta\) is determined by \(\Omega _1\) and \(\Omega _2\). A magnetic field applied to the subspace formed by \(|\uparrow \rangle\) and \(|\downarrow \rangle\) rotates the spin and \(|D\rangle\) is no longer the eigenstate. B In a generic three-level system, \(H_{\uparrow \downarrow }\) may be finite such that the lowest two states are not degenerate and are also coupled (blue arrow). C Adding gain/loss (wiggle vectors) and non-Hermitian couplings (magenta arrows with asymmetric heads) stabilizes \(|D\rangle\) as the eigenstate. D In the basis of dark and bright states, non-Hermiticity establishes a unidirectional coupling from \(|B\rangle\) to \(|D\rangle\)


\(|D\rangle\) disappears from the above equation and thus is invisible to the light fields. This textbook result is built upon the requirement that the Hamiltonian governing the subspace formed by \(|\uparrow \rangle\) and \(|\downarrow \rangle\) vanishes, \(H_{\uparrow \downarrow }=0\). This guarantees that \(|D\rangle\) remains stationary and the two pathways to \(|3\rangle\), one from \(|\uparrow \rangle\) via \(\Omega_1\) and the other from \(|\downarrow \rangle\) via \(-\Omega_2\), always destructively interfere.

In reality, \(H_{\uparrow \downarrow }\) may not vanish. As shown by Fig. 1B, the lasers coupling \(|\uparrow \rangle\) or \(|\downarrow \rangle\) to \(|3\rangle\) may be off-resonance such that \(|\uparrow \rangle\) and \(|\downarrow \rangle\) are not degenerate in the rotating frame. Alternatively, the direct couplings between \(|\uparrow \rangle\) and \(|\downarrow \rangle\) could be finite. In the most generic case, we write \(H_{\uparrow \downarrow }\) as

\(\begin{aligned} H_{\uparrow \downarrow }=\vec {B}_R\cdot \vec {S}, \end{aligned}\)
(4)

where \(\vec {B}_R=(B_R^x, B_R^y, B_R^z)\) is a real magnetic field, \(\vec {S}=\frac{1}{2}\vec {\sigma }\) and \(\vec {\sigma }\) represents the Pauli matrices. Unless \(\vec {B}_R\) aligns along the same direction as \(|D\rangle\), \(H_{\uparrow \downarrow }\) rotates \(|D\rangle\) on the Bloch sphere. As such, either the weights or the phases of \(\vert\uparrow\rangle\) and \(|\downarrow\rangle\) change as time goes by and the interference between the two pathways to \(|3\rangle\) is no longer destructive. In other words, a generic finite \(\vec {B}_R\) destroys the dark state.

To restore the dark state, we consider adding non-Hermitian terms to the Hamiltonian,

\(\begin{aligned} H_{\uparrow \downarrow }=\vec {B}\cdot \vec {S}=(\vec {B}_R+i\vec {B}_I)\cdot \vec {S}, \end{aligned}\)
(5)

where \(i\vec {B}_I\) represents an imaginary magnetic field. As shown in Fig. 1C, \(B^z_I\) characterizes the gain and loss in \(|\uparrow \rangle\) and \(|\downarrow \rangle\), respectively. \(B^x_I\) and \(B^y_I\) give rise to non-reciprocal couplings between \(|\uparrow \rangle\) and \(|\downarrow \rangle\). Such a spin is thus subject to a complex magnetic field \(\vec {B}=\vec {B}_R+i\vec {B}_I\), which has been realized in a variety of systems. One of the two spin states, say spin down, could be coupled to an excited state with a finite lifetime [20]. The strength of the laser and the detuning thus control the loss rate. Gains could also be, in principle, introduced by pumping atoms to the spin-up state from some other atomic states. Even when the gain is absent, the loss itself is sufficient to deliver a complex \({B}_z\), since \(-i B_{I}^z |\downarrow \rangle \langle \downarrow |=-i B_{I}^z/2 +iB_{I}^z S_z\). The extra constant \(-i B_{I}^z/2\) does not change any relevant results. To access a non-Hermitian off-diagonal term, experimentalists have used an ancillary state with losses to create an extra pathway to interfere with the ordinary Hermitian off-diagonal coupling [21]. The interference between these two pathways delivers a controllable non-reciprocal couplings between \(|\uparrow \rangle\) and \(|\downarrow \rangle\) and thus complex \(B_x\) and \(B_y\). It is worth pointing out that, in open systems, master equation is a more complete description than non-Hermitian Hamiltonians. Nevertheless, it has been well-understood that non-Hermitian Hamiltonians work well in time scales before the effects of jump operators become significant [22]. We thus focus on the non-Hermitian Hamiltonian in Eq. (5) in this manuscript.

To see that \(i\vec {B}_I\) can compensate \(\vec {B}_R\) and make \(|D\rangle\) stationary, we go to the basis formed by \(|D\rangle\) and \(|B\rangle\). We will see that \(i\vec {B}_I\) leads to unidirectional couplings between \(|D\rangle\) and \(|B\rangle\). We define a unitary transform \(U=e^{i\theta Sy}\) such that \(US_{z'} U^{-1}=S_z\), where \(S_{z'}=\cos (\theta )S_z+\sin (\theta )S_x\) is the projection of \(\vec {S}\) in the quantization axis along the direction of \(|D\rangle\). In this new basis, \(H_{\uparrow \downarrow }\rightarrow {H}'_{\uparrow \downarrow }=U{H}_{\uparrow \downarrow }U^{-1}=\vec {{B}}'\cdot \vec {S}\). A straightforward calculation show that

\(\begin{aligned} {B'}^x & =B^x\cos \theta -B^z\sin \theta ,\nonumber \\ {B'}^y & =B^y,\nonumber \\ {B'}^z & =B^x\sin \theta +B^z\cos \theta , \end{aligned}\)
(6)

where each component, \({B}'^{x,y,z}\), is complex. Viewing \(|D\rangle\) and \(|B\rangle\) as a two-level system, \(H'_{\uparrow \downarrow }\) can be rewritten as

\(\begin{aligned} H'_{\uparrow \downarrow }=\frac{\delta }{2}|D\rangle \langle D|-\frac{\delta }{2}|B\rangle \langle B|+t_L|D\rangle \langle B|+t_R|B\rangle \langle D|, \end{aligned}\)
(7)

where

\(\begin{aligned} & t_L=B_R'^x+B'^y_I+i(B'^x_I-B'^y_R), \nonumber \\ & t_R=B_R'^x-B'^y_I+i(B'^x_I+B'^y_R),\nonumber \\ & \delta =B'^z_R+iB'^z_I. \end{aligned}\)
(8)

A complex \(\vec {B}\), or equivalently a complex \(\vec {B}'\), means that all the coefficients in Eq. (7), in general, are complex and \(t_L\ne t_R^*\).

In ordinary dark states, the coupling with the bright state is absent. Here, such a coupling does not need to vanish. We only require that the coupling is a unidirectional one from \(|B\rangle\) to \(|D\rangle\), i.e., \(t_R=0\). If the system is initially prepared at the dark state, it could remain as an eigenstate of \(H'_{\uparrow \downarrow }\). In this sense, this is a dark state. We further set \(\text {Im}\delta =0\) to guarantee that the energy shift of \(|D\rangle\) and \(|B\rangle\) due to \(\vec {B}'\) is real. Satisfying both these two criteria, \(|D\rangle\) remains a stationary state of \(H'_{\uparrow \downarrow }\). We thus obtain, \(B'^x_I=-B'^y_R\), \(B'^y_I=B'^x_R\), \(B'^z_I=0\), which allows us to fix \(\vec {B}'_I\) using \(\vec {B}'_R\). We apply the inverse transform of Eq. (6), and the relationship between \(\vec {B}_R\) and \(\vec {B}_I\) is obtained,

\(\begin{aligned} B^x_I & =- B^y_R\cos \theta ,\nonumber \\ B^y_I & =B^x_R\cos \theta -B^z_R\sin \theta ,\nonumber \\ B^z_I & =B^y_R\sin \theta . \end{aligned}\)
(9)

The above set of equations has a clear physical meaning. When the y-component of the real magnetic field \(B^y_R\) is finite, \(|D\rangle\) tends to rotate about the y axis, as shown in Fig. 1. Consequently, \(\langle S^z\rangle\) (\(\langle S^x\rangle\)) tends to decrease (increase). To compensate for the increase of \(\langle S^z\rangle\), an imaginary magnetic field \(iB^z_I\) should be added in the z-direction, resulting in a gain in \(|\uparrow \rangle\) and a loss in \(|\downarrow \rangle\). Similarly, an imaginary magnetic field \(iB^x_I\) is required to cancel the increase of \(\langle S^x\rangle\). As such, \(|D\rangle\) remains stationary due to the interplay between a real magnetic field in the y direction and an imaginary field having finite projections in both the x and z directions. Similar discussions apply to cases of finite \(B^x_R\) and \(B^{z}_R\), which can also be compensated by corresponding imaginary magnetic fields.

The above discussions of \(\Lambda\) systems lay the foundation for using non-Hermiticity to restore dark states in both few-body and many-body systems. Here, we apply this protocol to study flat band physics, which is of particular interest in many-body physics [6,7,8,9,10]. Despite the fact that the very rich models of flat bands appear different from each other, the essential physics is the same. In the lattice model, \(|\uparrow \rangle\) and \(|\downarrow \rangle\) in Fig. 1 correspond to two lattice sites in the localized orbital. \(\Omega _1\) and \(\Omega _2\) are now the tunneling to a site \(|3\rangle\) outside the localized orbital. Our scheme applies to generic perturbations that demolish the destructive interference between the two pathways to \(|3\rangle\) and thus restore the flat bands.

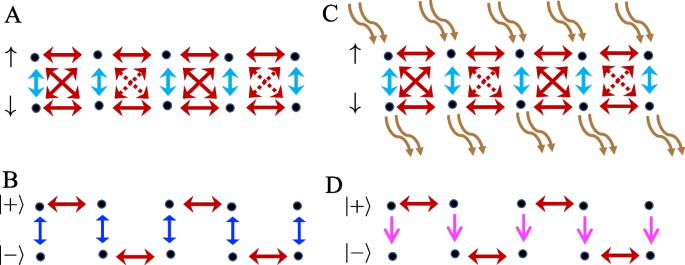
As a concrete example, we consider a lattice model as shown by Fig. 2B,

\(\begin{aligned} H_L & =\sum _{n\sigma } (\frac{t}{2} a^\dagger _{n\sigma }a_{n+1\sigma }+h.c.)+\sum _{n,\sigma \ne \sigma '} (-1)^n(\frac{t}{2}a^\dagger _{n\sigma }a_{n+1\sigma '}\nonumber \\ & \quad +h.c.)+\sum _n i\Gamma (-a^\dagger _{n\uparrow } a_{n\uparrow }+a^\dagger _{n\downarrow } a_{n\downarrow })+(\Omega _{\bot } a^\dagger _{n\uparrow } a_{n\downarrow }+h.c.), \end{aligned}\)
(10)

where \(a^\dagger _{n\sigma }\) is the creation operator at site n for spin-\(\sigma\), \(\Omega _{\bot } = \Omega _x-i\Omega _y\), and \(\sigma =\uparrow , \downarrow\). t/2 represents the tunneling strength, \(\Omega _{x,y}\) denotes the onsite spin flip strength, and \(\Gamma\) is the strength of the loss and gain. As shown by Fig. 2A, when \(\Gamma =\Omega _x=\Omega _y=0\), \(H_L\) could be regarded as a generalized Crutz ladder, where the factor \((-1)^n\) in \(H_L\) leads to a unit cell composed of four lattice sites [19]. It can be realized by applying a Raman lattice to atoms with two hyperfine spin states [18, 19]. Whereas the experiment has been focusing on the hermitian part of Eq. (10) [18], it is straightforward to add losses and/or gains to access a finite \(\Gamma\). An extra uniform coupling, such as rf coupling with an appropriately chosen phase relative to the Raman coupling, gives rise to a finite \(\Omega _x\) and \(\Omega _y\). A transformation \(\tilde{a}^\dagger _{n\uparrow }=(-1)^n{a}^\dagger _{n\uparrow }\) halves the unit cell and \(H_L\) describes two coupled bands with different parity. This model can be realized by periodically driving the lattice using two frequencies [9, 10].

Fig. 2
figure 2

A A generalized Crutz ladder. Dashed arrows denote the alternating sign change of the intersite spin flipping term. B Rewriting the generalized Crutz ladder in the basis of \(|+\rangle _n\) and \(|-\rangle _n\) leads to a two-leg SSH chain with glide reflection symmetry. C Adding gain and losses to the generalized Crutz ladder is equivalent to a two-leg SSH chain coupled by unidirectional hoppings in (D)


The model in Eq. (10) was recently studied in the context of non-Hermitian skin effects [23]. Here, we consider different physics regarding flat band and edge states. When \(\Gamma =\Omega _x=\Omega _y=0\), it has been shown that flat bands arise since the eigenstates of \(H_L\) are localized orbitals due to destructive interference between two pathways, one from the spin conserved coupling and the other from spin flipped couplings [9]. For more generic cases, it is more convenient to switch to a different basis \(|+\rangle _n=\frac{1}{\sqrt{2}}(|\uparrow \rangle _n+|\downarrow \rangle _n)\), \(|-\rangle =\frac{1}{\sqrt{2}}(|\uparrow \rangle _n-|\downarrow \rangle _n)\), where the localized orbitals can be best visualized as that in Fig. 1D. We define \(b^\dagger _{n\uparrow }=(a^\dagger _{n\uparrow }+ a^\dagger _{n\downarrow })/\sqrt{2}\), \(b^\dagger _{n\downarrow }=(a^\dagger _{n\uparrow }-a^\dagger _{n\downarrow })/\sqrt{2}\), and we obtain \(H_L=\sum _n H_n\), where

\(\begin{aligned} H_n&= t (b^\dagger _{2n\uparrow }a_{2n+1\uparrow }+b^\dagger _{2n+1\downarrow }b_{2n+2\downarrow }+h.c.)+\Omega _x( b^\dagger _{n\uparrow }b_{n\uparrow }\nonumber \\&\quad -b^\dagger _{n\downarrow }b_{n\downarrow }) +(-i\Gamma -i\Omega _y) b^\dagger _{n\uparrow } b_{n\downarrow }+(-i\Gamma +i\Omega _y) b^\dagger _{n\downarrow } b_{n\uparrow }. \end{aligned}\)
(11)

This model describes two chains coupled by asymmetric hoppings \(t_{\uparrow }=-i\Gamma -i\Omega _y\) and \(t_{\downarrow }=-i\Gamma +i\Omega _y\), as shown by Fig. 2B. It is useful to point out the connection between this model and its Hermitian counterpart. When \(\Omega _x=\Gamma =0\), \(H_L\) reduces to a two-leg SSH ladder with glide reflection symmetry [19]. Alternatively, this model can also be viewed as an SSH chain with long-range couplings or enlarged unit cells [24,25,26,27,28,29,30,31, 31, 32]. For convenience, we will consider it as a ladder formed by two SSH chains. In the Hermitian model, flat bands arise when \(\Omega _y=0\). As seen from Fig. 2B, each SSH chain consists of decoupled dimers in the bulk. Each eigenstate is composed of two sites in each chain. At the boundary, an isolated site in a single chain is decoupled from the bulk and gives rise to a zero-energy edge state. In the presence of a finite \(\Omega _y\), these two SSH chains are coupled and energy bands are no longer flat.

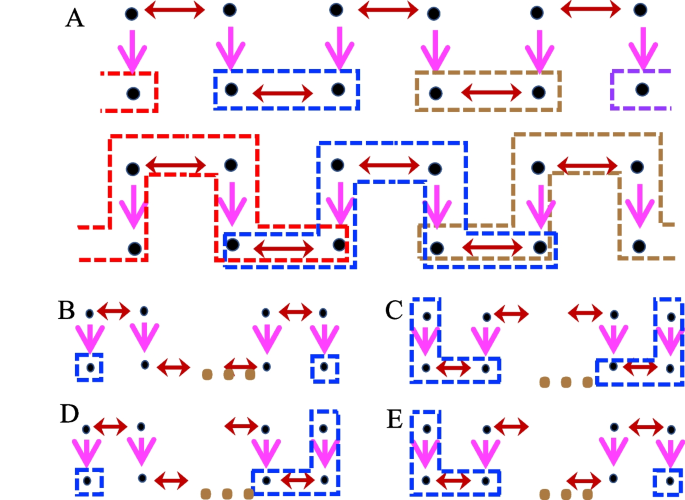
We now move on to consider the generic parameter regime, \(\Gamma , \Omega _{x,y}, t\ne 0\). To restore the flat bands, a finite \(\Gamma =\pm \Omega _y\) can be chosen such that the two SSH chains are coupled by unidirectional hoppings. For instance, when \(\Gamma =-\Omega _y\), a particle can hop from the upper chain to the lower one, not vice versa, as shown by Fig. 2D. As such, the eigenstates in the bulk are all localized ones. As shown in Fig. 3, there are two sets of such localized orbitals. To see their origin, we consider a local Hamiltonian in the basis formed by \(|-\rangle _{n-2}\), \(|-\rangle _{n-1}\), \(|+\rangle _{n}\), \(|+\rangle _{n+1}\), \(|-\rangle _{n+2}\), \(|-\rangle _{n+3}\),

\(\begin{aligned} h=\left( \begin{array}{cccccc} -\Omega _x & t & 0 & 0 & 0& 0 \\ t & -\Omega _x & -2i \Gamma & 0 & 0 & 0 \\ 0 & 0& \Omega _x & t & 0 & 0 \\ 0 & 0 & t & \Omega _x& 0 & 0 \\ 0 & 0 & 0 & -2i \Gamma & -\Omega _x& t \\ 0 & 0& 0 & 0 & t & -\Omega _x \end{array}\right) . \end{aligned}\)
(12)

Fig. 3
figure 3

A Each state in the first set of localized orbitals consists of two lattice sites in the lower chain. Different colors are used to distinguish orbitals at different locations. Another set of localized orbitals, each of which consists of two sites in the upper chain and four sites in the lower chain. B–E Blue boxes highlight the locations of edge states, which consist of either one or three lattice sites. Depending on whether the number of lattice sites is even or odd, there are four possibilities to arrange localized states at edges


As shown by Fig. 2D, a particle on any site in the lower chain cannot tunnel to the upper chain. As such, the subspace formed by the above six basis states is decoupled from the rest of the system.

We denote the eigenstates of h as \(\phi _i\), where \(i=1,2,3,4,+,-\), i.e., \(h\phi _i=E_i\phi _i\). Four of such eigenstates have finite occupancy only at the lower chain, \(\phi _1=(1, 1, 0,0,0,0)^T/\sqrt{2}\), \(\phi _2=(1, -1, 0,0,0,0)^T/\sqrt{2}\), \(\phi _3=(0,0,0,0,1,1)^T/\sqrt{2}\), \(\phi _4=(0,0,0,0,1,-1)^T/\sqrt{2}\), where T denotes the transpose of a matrix. These states provide us with the first set of localized eigenstates shown in Fig. 3A,

\(\begin{aligned} |D^{\pm }\rangle _{n\downarrow }=D^\dagger _{n\downarrow \pm }|0\rangle \end{aligned}\)
(13)

where \(D^\dagger _{n\downarrow \pm }= \frac{1}{\sqrt{2}}(b^\dagger _{n\downarrow }\pm b^\dagger _{n+1\downarrow })\). The energy is given by

\(\begin{aligned} E_{\downarrow \pm }=-\Omega _x\pm t. \end{aligned}\)
(14)

Apparently, \(|D^\pm \rangle _{n\downarrow }\) is decoupled from the rest of the system. The other two eigenstates, \(\phi _{\pm }\), have finite occupancy in both chains, providing the other set of localized orbitals of \(H_L\),

\(\begin{aligned} |D^{\pm }\rangle _{n\uparrow }=D^\dagger _{n\uparrow \pm }|0\rangle , \end{aligned}\)
(15)

where \(D^\dagger _{n\uparrow \pm }=\phi ^T_{\pm }\cdot \mathcal B\) and \(\mathcal B\) is a short-hand notation, \(\mathcal B=( b^\dagger _{n-2\downarrow }, b^\dagger _{n-1\downarrow }, b^\dagger _{n\uparrow }, b^\dagger _{n+1\uparrow }, b^\dagger _{n+2\downarrow }, b^\dagger _{n+3\downarrow })^T\). The eigenenergies are

\(\begin{aligned} E_{\uparrow \pm }=\Omega _x\pm t. \end{aligned}\)
(16)

We thus conclude that there are four flat bands in the bulk, whose energies are written in Eqs. (14, 16). When \(\Omega _x=0\), the number of flat bands reduces to two, and each band is doubly degenerate.

In addition to the localized orbitals in the bulk, it is also interesting to investigate the edge states. As shown by Fig. 3B-E, there are two types of localized states at the edges. One consists of a single lattice site at either end of the lower chain. Due to the unidirectional couplings between the up and lower chains, such states are apparently isolated from other lattice sites and the energies are given by \(E_{e\downarrow }=-\Omega _x\). Another type of edges state are formed by three lattice sites. For instance, the edge state at the right end of the lattice with odd number of lattice sites arises from the Hamiltonian,

\(\begin{aligned} h_{e\uparrow }=\left( \begin{array}{ccc} \Omega _x & 0 & 0 \\ -2i\Gamma & -\Omega _x & t\\ 0 & t& -\Omega _x \end{array}\right) , \end{aligned}\)
(17)

where the basis states are \(|+\rangle _L\), \(|-\rangle _L\), and \(|-\rangle _{L-1}\). L is the number of lattice sites. We denote the eigenstates of \(h_{e\uparrow }\) as \(\tilde{\phi }_i\), where \(i=1,2,3\). Two of the three eigenstates are \((0,1,1)^T/\sqrt{2}\), and \((0,1,-1)^T/\sqrt{2}\). They coincide with the localized states in the bulk, i.e., \(|D^{\pm }\rangle _{L-1}\). The third state could be expressed as

\(\begin{aligned} |E^{\uparrow }\rangle _{n\uparrow }=\tilde{\phi }^T_3\cdot \mathcal {\tilde{B}} |0\rangle , \end{aligned}\)
(18)

where \(\mathcal {\tilde{B}} =(b^\dagger _{L\uparrow }, b^\dagger _{L\downarrow }, b^\dagger _{L-1\uparrow })^T\). Its energy is given by \(E_{e\uparrow }=\Omega _x\).

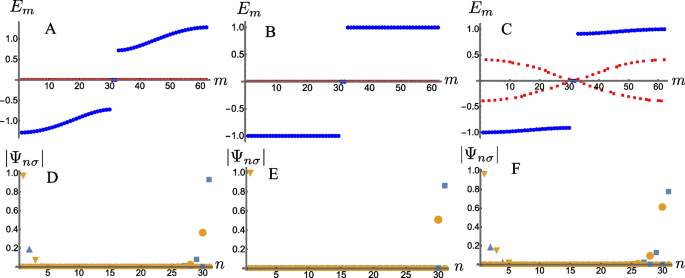
Whereas we have been focusing on \(\Gamma =|\Omega _y|\), it is useful to discuss more generic scenarios. When \(\Gamma \ne |\Omega _y|\), the coupling between the upper and lower chains are no longer unidirectional and the previously discussed localized orbitals are going to be coupled to each other. Nonetheless, the bandwidth is small when either \(t_{\uparrow }\) or \(t_{\downarrow }\) is small. In particular, the energy gap between the bulk states and the edge state may remain finite before crossing a critical point, as shown in Fig. 4. If we consider \(\Gamma>-\Omega _y\), the wavefunction of the zero-energy edge states at the left end is written as

\(\begin{aligned} |L\rangle =\sum _{n\sigma }\Psi _{n\sigma }b^\dagger _{n\sigma }|0\rangle . \end{aligned}\)
(19)

Fig. 4
figure 4

A-C The real part (blue dots) and the imaginary part (red boxes) of the energy. t has been chosen as the energy scale, \(\Omega _y=0.3\), \(\Omega _x=0\). \(\Gamma =-0.1, -0.3, -0.5\) in A, B, C, respectively. D-F The wavefunctions of the corresponding edge states. Blue up triangles and brown down triangles represent \(|\Psi _{n\uparrow }|^2\) and \(|\Psi _{n\downarrow }|^2\) of the left edge state. Blue boxes and brown dots represent \(|\Psi _{n\uparrow }|\) and \(|\Psi _{n\downarrow }|\) of the right edge state


When \(\Omega _x=0\), a simple analytical expression of the \(\Psi _{n\sigma }\) exits. Using the zero energy solution to the Schrodinger equation, we find that \(\Psi _{n\sigma }\) satisfies

\(\begin{aligned} & \Psi _{n\uparrow }=0, \,\,\, n\in even,\end{aligned}\)
(20)

\(\begin{aligned} & \Psi _{n\downarrow }=0, \,\,\, n\in odd, \end{aligned}\)
(21)

and

\(\begin{aligned} & \Psi _{2n+1\uparrow }= \left( \frac{t_{\uparrow } t_{\downarrow }}{t^2}\right) ^n \frac{t_{\uparrow }}{t}\Psi _{0\downarrow }, \end{aligned}\)
(22)

\(\begin{aligned} & \Psi _{2n\downarrow }=\left( \frac{t_{\uparrow } t_{\downarrow }}{t^2}\right) ^n \Psi _{0\downarrow }. \end{aligned}\)
(23)

We thus see that the wavefunction decays exponentially with the localization length \(\sigma =\ln ^{-1}( \frac{t^2}{|t_{\uparrow } t_{\downarrow }|})\).

Similar discussions apply to the edge state at the right end, whose wavefunction exponentially decays with the same localization length. We thus conclude that the critical point is determined by \(t_{\uparrow } t_{\downarrow }=t^2\). When \(\Gamma\) continuously decreases down to \(-\Omega _y\), \(t_{\uparrow }\) vanishes and the localization length becomes zero, as previously discussed. Further decreasing \(\Gamma\), \(t_{\uparrow }\) changes sign and the energy of a bulk state acquires a finite imaginary part. Nonetheless, the energy of the edge state remains zero. Only when \(|t_{\uparrow }t_{\downarrow }|\) becomes larger again, the edge states disappear and any energy eigenstate has a finite imaginary part of the energy.

Since \(t_{\uparrow }\) and \(t_{\downarrow }\) depend on \(\Gamma\) and \(\Omega _y\), it is worth highlighting a case of particular interest. Consider \(\Omega _y>t\), when \(\Gamma =0\), the model reduces to an ordinary SSH chain in the regime without an edge state, distinct from the case where the edge states exist if \(\Omega _y. Turning on a finite \(\Gamma\), \(|t_{\downarrow }t_{\uparrow }|=\Omega _y^2-\Gamma ^2\) decreases. At the critical point, \(\Omega _y^2-\Gamma ^2=t^2\), and the edge states appear. This means that non-Hermiticity could be implemented as a constructive means to recover the edge state and turn a trivial phase to a nontrivial one.

Whereas we have considered a vanishing \(\Omega _x\), similar discussions apply to a finite \(\Omega _x\). Despite the fact that there are quantitative differences such as finite energies of the edge states and two degenerate bands in the bulk splitting into four bands, the essential physics of the existence of edge states remains the same.

In the above discussions, we have been focusing on non-interacting systems. It is useful to comment on the interaction effects. Since each of the localized orbitals in the flat band limit occupies multiple sites, on-site interactions become sufficient to induce novel quantum many-body states. When we consider a repulsive onsite interaction,

\(\begin{aligned} H_{int}=U\sum _n b^\dagger _{n\uparrow }b_{n\uparrow }b^\dagger _{n\downarrow }b_{n\downarrow }, \end{aligned}\)
(24)

where \(U>0\), occupying overlapping localized orbitals in Fig. 3 leads to an energy penalty. Such an energy penalty gives rise to certain novel quantum phases at the ground state. For instance, when \(\Omega _x<0\) and \(0, the energy gap between the lowest two bands is written as \(\Delta =E_{\uparrow +}-E_{\uparrow -}=2t\). When \(U\ll t\), it is sufficient to project \(H_{int}\) to the lowest band. At filling factor of 1/8, the lowest band is half filled. Due to the vanishing bandwidth, bosons do not condense and only one of the two successive localized orbitals, \(|D^-\rangle _{n\uparrow }\), is occupied to avoid the energy penalty. As such, a charge density wave arises as the ground state, and the wavefunction is written as

\(\begin{aligned} |G\rangle =\prod _{n\in even}D^\dagger _{n\uparrow +}|0\rangle . \end{aligned}\)
(25)

or \(\prod _{n\in odd}D^\dagger _{n\uparrow +}|0\rangle\). Doping this charge density wave, overlapping localized orbitals lead to density assisted tunneling and pairing hoppings and a supersolid or paired superfluid may appear [33,34,35].

We have shown that non-Hermitian Hamiltonians could be implemented to recover the dark states. Applying this scheme to lattice systems could create or recover localized eigenstates, including flat bands in the bulk and edge states at the boundaries. We hope that our work will stimulate more interest in studying such non-Hermiticity restored dark states and their applications in many-body physics.

Data availability

All data are available upon request through the authors.

References

  1. M.O. Scully, M.S. Zubairy, Quantum optics (Cambridge university press, Cambridge, 1997)

  2. M. Fleischhauer, A. Imamoglu, J.P. Marangos, Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 77(2), 633–673 (2005)

  3. J.P. Marangos, Electromagnetically induced transparency. J. Mod. Opt. 45(3), 471–503 (1998)

  4. K.J. Boller, A. Imamoğlu, S.E. Harris, Observation of electromagnetically induced transparency. Phys. Rev. Lett. 66(20), 2593 (1991)

  5. S. Diehl, A. Micheli, A. Kantian, B. Kraus, H. Büchler, P. Zoller, Quantum states and phases in driven open quantum systems with cold atoms. Nat. Phys. 4(11), 878–883 (2008)

  6. S. Mukherjee, A. Spracklen, D. Choudhury, N. Goldman, P. Öhberg, E. Andersson, R.R. Thomson, Observation of a localized flat-band state in a photonic Lieb lattice. Phys. Rev. Lett. 114(24), 245504 (2015)

  7. M.R. Slot, T.S. Gardenier, P.H. Jacobse, G.C. Van Miert, S.N. Kempkes, S.J. Zevenhuizen, C.M. Smith, D. Vanmaekelbergh, I. Swart, Experimental realization and characterization of an electronic Lieb lattice. Nat. Phys. 13(7), 672–676 (2017)

  8. T. Zhang, G.B. Jo, One-dimensional sawtooth and zigzag lattices for ultracold atoms. Sci. Rep. 5(1), 16044 (2015)

  9. S.L. Zhang, Q. Zhou, Shaping topological properties of the band structures in a shaken optical lattice. Phys. Rev. A 90(5), 051601 (2014)

  10. J.H. Kang, Y.-I. Shin, Topological floquet engineering of a one-dimensional optical lattice via resonant shaking with two harmonic frequencies. Phys. Rev. A 102(6), 063315 (2020)

  11. D. Leykam, S. Flach, Y.D. Chong, Flat bands in lattices with non-hermitian coupling. Phys. Rev. B 96(6), 064305 (2017)

  12. H. Ramezani, Non-hermiticity-induced flat band. Phys. Rev. A 96(1), 011802 (2017)

  13. T. Biesenthal, M. Kremer, M. Heinrich, A. Szameit, Experimental realization of PT-symmetric flat bands. Phys. Rev. Lett. 123(18), 183601 (2019)

  14. S. Zhang, L. Jin, Non-Hermitian Aharonov-Bohm cage. (2020). arXiv preprint arXiv:2005.01044

  15. S. Zhang, L. Jin, Localization in non-Hermitian asymmetric rhombic lattice. Phys. Rev. Res. 2(3), 033127 (2020)

  16. W. Maimaiti, A. Andreanov, Non-Hermitian flat-band generator in one dimension. Phys. Rev. B 104(3), 035115 (2021)

  17. X. Li, J. Liu, T. Liu, Localization-delocalization transitions in non-Hermitian Aharonov-Bohm cages. Front. Phys. 19(3), 33211 (2024)

  18. E. Zhao, T.H. Mak, C. He, Z. Ren, K.K. Pak, Y.J. Liu, G.B. Jo, Observing a topological phase transition with deep neural networks from experimental images of ultracold atoms. Opt. Express 30(21), 37786–37794 (2022)

  19. S.L. Zhang, Q. Zhou, Two-leg Su-Schrieffer-Heeger chain with glide reflection symmetry. Phys. Rev. A 95(6), 061601 (2017)

  20. J. Li, A.K. Harter, J. Liu, L. de Melo, Y.N. Joglekar, L. Luo, Observation of parity-time symmetry breaking transitions in a dissipative Floquet system of ultracold atoms. Nat. Commun. 10(1), 855 (2019)

  21. Q. Liang, D. Xie, Z. Dong, H. Li, H. Li, B. Gadway, W. Yi, B. Yan, Dynamic signatures of non-Hermitian skin effect and topology in ultracold atoms. Phys. Rev. Lett. 129(7), 070401 (2022)

  22. S. Dürr, J.J. García-Ripoll, N. Syassen, D.M. Bauer, M. Lettner, J.I. Cirac, G. Rempe, Lieb-liniger model of a dissipation-induced Tonks-Girardeau gas. Phys. Rev. A At. Mol. Opt. Phys. 79(2), 023614 (2009)

  23. L. Zhou, H. Li, W. Yi, X. Cui, Engineering non-Hermitian skin effect with band topology in ultracold gases. Commun. Phys. 5(1), 252 (2022)

  24. C. Li, A.E. Miroshnichenko, Extended SSH model: Non-local couplings and non-monotonous edge states. Physics 1(1), 2–16 (2018)

  25. J. Zurita, C. Creffield, G. Platero, Tunable zero modes and quantum interferences in flat-band topological insulators. Quantum 5, 591 (2021)

  26. R. Dias, A. Marques, Long-range hopping and indexing assumption in one-dimensional topological insulators. Phys. Rev. B 105(3), 035102 (2022)

  27. F. Ares, S. Murciano, P. Calabrese, Symmetry-resolved entanglement in a long-range free-fermion chain. J. Stat. Mech. Theory Exp. 2022(6), 063104 (2022)

  28. K. Qian, D.J. Apigo, K. Padavić, K.H. Ahn, S. Vishveshwara, C. Prodan, Observation of majorana-like bound states in metamaterial-based kitaev chain analogs. Phys. Rev. Res. 5(1), L012012 (2023)

  29. X. Zhou, J.S. Pan, S. Jia, Exploring interacting topological insulator in the extended Su-Schrieffer-Heeger model. Phys. Rev. B 107(5), 054105 (2023)

  30. N. Ara, R. Basu, Topological phases in coupled polyyne chains. J. Phys. Condens. Matter 35(38), 385502 (2023)

  31. S. Mandal, S. Kar, Topological solitons in a Su-Schrieffer-Heeger chain with periodic hopping modulation, domain wall, and disorder. Phys. Rev. B 109(19), 195124 (2024)

  32. M. Ghuneim, R.W. Bomantara, Topological phases of tight-binding trimer lattice in the BDI symmetry class. J. Phys. Condens. Matter 36(49), 495402 (2024)

  33. S.D. Huber, E. Altman, Bose condensation in flat bands. Phys. Rev. B Condens. Matter Mater. Phys. 82(18), 184502 (2010)

  34. S. Takayoshi, H. Katsura, N. Watanabe, H. Aoki, Phase diagram and pair tomonaga-luttinger liquid in a bose-hubbard model with flat bands. Phys. Rev. A At. Mol. Opt. Phys. 88(6), 063613 (2013)

  35. M. Tovmasyan, E.P. Van Nieuwenburg, S.D. Huber, Geometry-induced pair condensation. Phys. Rev. B 88(22), 220510 (2013)

Acknowledgements

The authors thank Hui Hu for inviting the submission.

Funding

This work is supported by the Air Force Office of Scientific Research under award number FA9550-23-1-0491.

Author information

Authors and Affiliations

Department of Physics and Astronomy, Purdue University, West Lafayette, IN, 47907, USA
Qi Zhou

Contributions

QZ conceived the project and conducted analytical and numerical calculations.

Corresponding author

Correspondence to Qi Zhou.

Ethics declarations

Competing interests

The author declares no competing interests.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

[Source: https://link.springer.com/article/10.1007/s43673-025-00148-8]