Abstract
I briefly review the canonical vorticity theoretical framework and its applications in collisionless, magnetized plasma physics. The canonical vorticity is a weighted sum of the fluid vorticity and the magnetic field and is equal to the curl of the canonical momentum. By taking this variable as the primary variable instead of the magnetic field, various phenomena that require non-MHD effect in their scrutiny can be simplified. Two examples are given, namely magnetic reconnection and magnetogenesis, and exactly how the canonical vorticity framework simplifies their analyses is described. Suggestions for future work are also delineated.
1 Introduction
Plasma physics is the study of the collective behavior of statistically large numbers of charged particles. Because of these large numbers, one can construct a distribution function for each species in phase space and observe the evolution of this function in time instead of following the dynamics of individual particles. One can then simplify things a little further by defining moments of the distribution function as fluid variables and constructing fluid equations, although a particular closure must be assumed to close the system of equations.
Because the individual species in a plasma typically has charge, the forces that govern them are the Lorentz force and the pressure force, and so in the collisionless limit the fluid momentum equation usually contains these two terms. The magnetic field in particular plays an important role, and in the ideal magnetohydrodynamic (MHD) approximation, it is in fact frozen into the plasma fluid. Thus, many magnetized plasma phenomena have been studied with the magnetic field as the primary variable.
For instance, magnetic reconnection is a plasma phenomenon in which magnetic fields change topology and release their stored energy into plasma kinetic energy [1, 2]. Because ideal Ohm’s law and the entailing magnetic flux conservation forbids magnetic reconnection in ideal MHD, the de-facto standard analysis is to include various terms such as the electron inertia term in Ohm’s law to construct a generalized Ohm’s law, and then examine the roles of the individual terms [3, 4]. The ways in which these terms break the frozen-in condition is typically deemed as the important understanding, and significant research effort has gone into this understanding.
However, this line of thought naturally begs the question: even in regimes where ideal MHD is violated, can one find a quantity that is conserved, similar to magnetic flux in ideal MHD? The answer is a resounding “yes,” and the flux associated with a quantity called “canonical vorticity” is the ideally conserved quantity [5,6,7,8,9,10,11,12,13,14]. One can thus construct a theoretical framework where canonical vorticity is the primary variable rather than the magnetic field, and even in regimes where canonical vorticity flux is not conserved, the framework itself proves to be important in improving the physical understanding and intuition behind various plasma phenomena.
Another important process in which magnetic flux is not conserved is magnetogenesis, or magnetic field generation. Here, the magnetic flux is initially zero but becomes finite and so its conservation is violated. Historically, two mechanisms are most popularly invoked for magnetogenesis, namely the Weibel instability [15] and the Biermann battery effect [16]. However, a generalization of spontaneous magnetogenesis is lacking and will be shown to be possible by focusing on canonical vorticity dynamics.
In this paper, I briefly review the canonical vorticity framework and its applications in two important plasma phenomena: magnetic reconnection and magnetogenesis. Explanation of the two complicated processes is vastly simplified, owing to there being only two terms that completely describe the time evolution of canonical vorticity. In particular, magnetic reconnection is shown to be a rather natural and not surprising process, and magnetogenesis is shown to be only possible, at least initially, by the finite electron pressure tensor.
2 Canonical vorticity framework
Let us first start with the Vlasov equation for each plasma species \(\sigma\) and its phase-space distribution function \(f_{\sigma }=f_{\sigma }\left( \textbf{x},\textbf{v}\right)\):
where \(q_{\sigma }\) and \(m_{\sigma }\) are the species charge and mass, respectively, and \(\textbf{E}\) and \(\textbf{B}\) are the electric and magnetic fields in the system that obey Maxwell’s equations and provide the Lorentz force. Note that collisions have been ignored in this collisionless limit. Taking the first moment of this equation yields the fluid equation of motion,
where \(n_{\sigma }=\int f_{\sigma }d^{3}\textbf{v}\) is the species density, \(\textbf{u}_{\sigma }=\int \textbf{v}f_{\sigma }d^{3}\textbf{v}\) is the mean fluid velocity, and \(\overleftrightarrow {\textbf{p}}_{\sigma }=m_{\sigma }\int \left( \textbf{v}-\textbf{u}_{\sigma }\right) \left( \textbf{v}-\textbf{u}_{\sigma }\right) f_{\sigma }d^{3}\textbf{v}\) is the fluid pressure tensor. The intention is to take the curl of Eq. 2, and it is useful to note that
first by Faraday’s law and second by the vector identity \(\nabla V^{2}/2=\textbf{V}\cdot \nabla \textbf{V}+\textbf{V}\times \nabla \times \textbf{V}\) for any vector \(\textbf{V}\). Taking the curl of Eq. 2 thus yields, defining the fluid vorticity \(\Omega _{\sigma }=\nabla \times \textbf{u}_{\sigma }\),
Collecting the temporal and spatial derivatives, one obtains the canonical induction equation [14]:
Here, the quantity \(\textbf{Q}_{\sigma }\) is “canonical vorticity,” defined as
which is the curl of the canonical momentum \(\textbf{P}_{\sigma }=m_{\sigma }\textbf{u}_{\sigma }+q_{\sigma }\textbf{A}\) where \(\textbf{A}\) is the magnetic vector potential.
Equation 6 shows that the time evolution of \(\textbf{Q}_{\sigma }\) is determined by only two terms on the right-hand side. Ignoring the pressure term, Eq. 6 is isomorphic to the MHD magnetic induction equation,
where \(\textbf{U}\) is the plasma flow velocity. Because Eq. 8 signifies that magnetic flux \(\Phi _{B}=\int \textbf{B}\cdot d\textbf{s}\) is a conserved quantity in the plasma frame and equivalently that \(\textbf{B}\) advects with \(\textbf{U}\), Eq. 6 without the pressure term signifies that \(\textbf{Q}_{\sigma }\) advects with \(\textbf{u}_{\sigma }\) and that the canonical vorticity flux \(\Phi _{Q}=\int \textbf{Q}_{\sigma }\cdot d\textbf{s}\) is a conserved quantity in the frame moving with \(\textbf{u}_{\sigma }\).
The final term in Eq. 6 arises due to a finite pressure tensor, and is called the “canonical battery” term [14, 17]. If the pressure tensor is assumed to be isotropic, i.e., \(\overleftrightarrow {\textbf{p}}_{\sigma }=p_{\sigma }\overleftrightarrow {\textbf{I}}\) where \(\overleftrightarrow {\textbf{I}}\) is the identity matrix, the canonical battery term becomes
which is for the electron species is exactly the Biermann battery term [16]. If the density is uniform and/or the pressure is barotropic so that \(p_{\sigma }=p_{\sigma }\left( n_{\sigma }\right)\), this battery term is identically zero.
3 Magnetic reconnection
Now let us see how the canonical vorticity framework facilitates the understanding of magnetic recon3nection. First, I show that the generalized Ohm’s law including the Hall, electron inertia, and electron pressure terms is identical to the electron equation of motion, i.e., the electron version of Eq. 2. Such generalized Ohm’s law is
where \(d/dt=\partial /\partial t+\textbf{u}_{e}\cdot \nabla\) is the total derivative, n is the plasma density, and e is the elementary charge. Using \(e=-q_{e}\) and \(\textbf{U}\simeq \textbf{u}_{i}\) so that \(\textbf{U}\times \textbf{B}-\textbf{J}\times \textbf{B}/ne\simeq \textbf{u}_{e}\times \textbf{B}\) and rearranging shows that Eq. 11 is equivalent to Eq. 2. Therefore, because Eq. 6 was derived from Eq. 2, Eq. 6 contains all the information on Hall, electron inertia, and electron pressure terms.
Now that we have established the equivalence between the generalized Ohm’s law and the canonical induction equation, let us examine the physical meaning of canonical vorticity in magnetic reconnection. It is well known that during collisionless magnetic reconnection the Hall term is dominant over the \(\textbf{U}\times \textbf{B}\) term [18]. Comparing the magnitude of the two terms while assuming \(\textbf{U}\) is of the order of the Alfvén velocity \(v_{A}=B/\sqrt{\mu _{0}nm_{i}}\),
where \(\textbf{J}\sim \textbf{B}/\mu _{0}L\) by Ampère’s law and \(d_{i}\) is the collisionless ion skin depth. Therefore, the relevant length scales in collisionless magnetic reconnection is smaller than the ion skin depth. At these length scales, the ions may be assumed to be approximately stationary relative to the electrons which are still tied to the magnetic field lines, so \(\textbf{J}\simeq -ne\textbf{u}_{e}\). If constant density is further assumed, then the system is called electron-MHD or EMHD [6, 7]. The electron canonical vorticity may thus be written as
where \(d_{e}\) is the collisionless electron skin depth. Equation 18 shows that at length scales much larger than \(d_{e}\), \(\textbf{Q}_{e}\simeq -e\textbf{B}\), so canonical vorticity is identical to the magnetic field up to a constant factor. At length scales smaller than \(d_{e}\), however, \(\textbf{Q}_{e}\simeq m_{e}\nabla \times \textbf{u}_{e}\simeq ed_{e}^{2}\nabla ^{2}\textbf{B}\).
For simplicity, let us for now ignore the canonical battery term in Eq. 6. Then, in analogy to magnetic flux conservation in ideal MHD, the conserved quantity in the electron frame is
where \(\Gamma _{e}=\oint \textbf{u}_{e}\cdot d\textbf{l}\) is the electron circulation. Therefore, the magnetic field is free to reconnect and convert into electron flow while conserving \(\Phi _{Q}\). Such reconnection has also been referred to as “Hamiltonian magnetic reconnection [19]”.
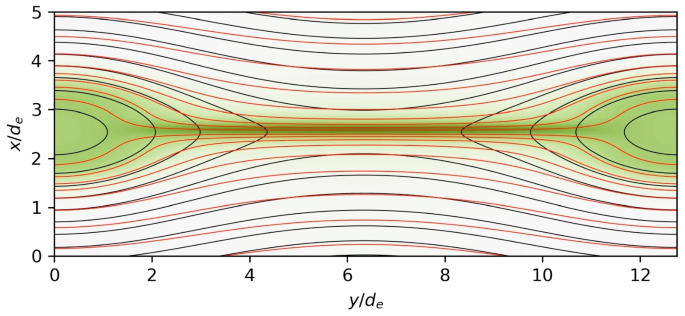
Figure 1 shows the magnetic field (black lines), electron canonical vorticity (red lines), and the out-of-plane electron flow velocity (green color) for a typical magnetic reconnection geometry. One can clearly see that while the magnetic fields are reconnecting, the canonical vorticity field lines are not reconnecting. The simulation details can be found in Refs. [12, 13].
In fact, the growth rate of magnetic reconnection can be calculated in a generic reconnection geometry [12, 13]. Because ions are stationary, quasi-neutrality dictates that the electron fluid is incompressible, so \(\nabla \cdot \textbf{u}_{e}=0\). Also, \(\nabla \cdot \textbf{Q}_{e}=0\) by definition. The y-component of Eq. 6 is then
where the total derivative \(d/dt=\partial /\partial t+\textbf{u}_e\cdot \nabla\). Now, letting the reconnecting magnetic field be in the y-direction that has an inflection point at \(x=0\), \(Q_{ex}\) must be zero near this point because reconnection of \(\textbf{Q}_{e}\) is forbidden. Also, one can let \(\partial /\partial z\rightarrow 0\) if two-dimensional reconnection is assumed. The above equation near \(x=0\) is now simplified as
whose solution is
which is an exponentially growing solution because the \(u_{ey}\) is the electron outflow that thus must have a positive gradient along y.
As reconnection proceeds and \(\Gamma _{e}\) increases while the length scale decreases due to \(\textbf{Q}_{e}\) flux pile-up, the electron fluid velocity becomes singular and builds up significant free energy. At the kinetic level, this signifies that the electron pressure tensor becomes significant and contributes greatly to balancing the reconnection electric field in Eq. 11. This also means that the canonical battery term in Eq. 6 becomes significant and eventually balances the advection term. This is the nonlinear saturated state of collisionless magnetic reconnection [14].
On top of these intuitive understandings, the canonical vorticity framework can also be used to explain the origin of anomalous ion heating during magnetic reconnection. In particular, the electron version of Eq. 2 can be solved for \(\textbf{E}\) as
This form of the electric field allows for the leveraging of the non-reconnection of \(\textbf{Q}_e\) shown in Fig. 1 in the inflow and outflow directions. For example, ignoring the pressure term for simplicity, the electric field in the inflow direction along the middle axis \(y=6.4d_e\) can be calculated to be [20]
which, if inserted in the criterion for stochastic ion heating [21, 22]
yields
where \(L_x\) is the length scale of the magnetic field, i.e., \(B_y^2/\left( \partial B_y^2/\partial x\right)\), and \(d_i\) is the ion skin depth. Because Eq. 27 is a prerequisite for collisionless magnetic reconnection, this means that stochastic ion heating is intrinsic to the process and is responsible for the strong ion heating. This fact, predicted by the canonical vorticity framework, has been verified through particle-in-cell simulations and further theoretical work [23,24,25].
4 Magnetogenesis
Another important problem in plasma physics is that of magnetogenesis, which concerns the spontaneous generation of magnetic fields in plasmas. There are two popular mechanisms for magnetogenesis, namely the Biermann battery effect [16] and the Weibel instability [15]. The Biermann battery effect arises due to a finite cross-product between density and pressure gradients in a plasma, and the Weibel instability is a kinetic effect that arises due to pressure anisotropy.
Using the canonical vorticity framework, the problem of magnetogenesis is vastly simplified. Let us focus once again on the electron canonical induction equation and on the fact that \(\textbf{Q}_{e}\simeq e\left( d_{e}^{2}\nabla ^{2}\textbf{B}-\textbf{B}\right)\) at electron scales. The spontaneous generation of \(\textbf{B}\) thus must entail the spontaneous generation of \(\textbf{Q}_{e}\). Now, Eq. 6 shows that when \(\textbf{Q}_{e}=0\) at \(t=0\),
which shows that only the canonical battery effect can be responsible for spontaneous generation of \(\textbf{Q}_{e}\) and thus \(\textbf{B}\).
The canonical battery term generalizes both magnetogenesis mechanisms that are in widespread use. It has already been shown to generalize the Biermann battery effect in Eq. 10 for an isotropic pressure. In fact, focusing on the generation of z-directed magnetic fields for simplicity and so examining the z-component of the canonical battery term, it can be dissected into three distinct terms:
where \(p_{eij}\) is the ijth component of the tensor \(\overleftrightarrow {\textbf{p}}_{e}\). The first term arises due to the finite density gradient and is a thus a Biermann-like term. The second term involves a finite off-diagonal component and signifies the mixing between \(p_{exx}\) and \(p_{eyy}\). This is in fact the term responsible for the Weibel instability; one can see this by noting that the Weibel instability is a one-dimensional instability, and the only term that survives if either \(\partial /\partial x\rightarrow 0\) or \(\partial /\partial y\rightarrow 0\) is assumed in Eq. 29 is the second term. The third term signifies a two-dimensionally localized pressure anisotropy, which is a new term.
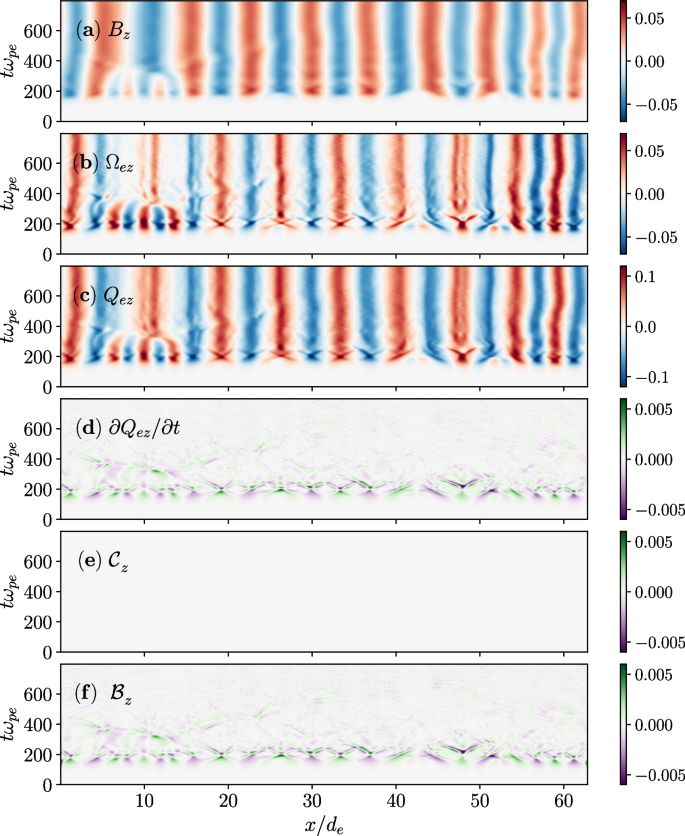
Figure 2 shows various terms in Eq. 6 that are involved in the Weibel instability. It can first be seen that that electron canonical vorticity has a similar structure to the magnetic field (Figs. 2a and c), showing that the former is indeed a proxy for the latter. The growth of the electron canonical vorticity is indeed entirely due to the electron canonical battery (Figs. 2d and f).
Various terms contributing to the magnetic field growth during Weibel instability. Shown are streak plots of the a magnetic field, b electron vorticity, c electron canonical vorticity, d time derivative of the electron canonical vorticity, e advective term (first term on the right-hand-side in Eq. 6), and f electron canonical battery term (last term in Eq. 6 ). Figure reproduced from [17]
The canonical battery term clarifies the physical origin of the Weibel instability, which is often attributed to pressure anisotropy. To be precise, it is the mixing of the pressure anisotropy that generates magnetic fields, instead of the anisotropy per se. In fact, a 2D-localized pressure anisotropy by itself creates magnetic fields without a need for the Weibel instability [17]. Various properties such as the temporal growth rate of the magnetic field and the energy spectra differ from the Weibel instability.
On top of the spontaneous magnetogenesis, the canonical vorticity framework can also be used to probe how seed magnetic fields generated by the process can be caught by the dynamo process. While the canonical battery term is responsible for seed magnetogenesis, as the system moves to larger and larger scales, the advection term must become more and more significant. Future work will be dedicated to how and when the weight in each term changes as the system evolves to a dynamo-dominated regime.
5 Discussion
It should be clear by now how the canonical vorticity framework can simplify extremely complicated phenomena in magnetized plasma physics. By focusing on the truly conserved quantity that is the canonical vorticity flux in the ideal regime and on the sole non-ideal term that arises due to the pressure tensor that is the canonical battery effect, a simple explanation of magnetic reconnection and magnetogenesis can be given.
The canonical battery term provides a simple way to gauge the importance of different effects during magnetogenesis. For large temperature gradient scales of \(L\gtrsim 100 d_e\), it is well-known that the Weibel instability dominates over the Biermann battery effect, which in turn dominates for \(L\lesssim 100d_e\) [26]. Comparing the terms responsible for Biermann effect and the Weibel instability in Eq. 29, one can easily see that the ratio of the importance of the two effects scales as \(T_\text {diag}/T_\text {off}:L/d_e\), where \(T_\text {diag}\) and \(T_\text {off}\) are the diagonal and off-diagonal terms of the temperature tensor. Typically, the diagonal component of the temperature tensor is much bigger than the off-diagonal component, and therefore the Weibel instability indeed dominates for very large temperature gradient length scales.
A similar analysis can be conducted for magnetic reconnection. As reconnection proceeds, at quasi-steady state the pressure anisotropy is known to settle close to the electron firehose instability criterion [27]. This fact can be easily derived by balancing the advection and battery terms in Eq. 6 for \(d_e
An obvious future work is to extend this framework to relativistic regimes. In this regime, the fluid momentum is not equal to the fluid velocity, because \(\textbf{p}_{\sigma }=\int \gamma m_{\sigma }\textbf{v}f_{\sigma }d^{3}\textbf{v}\) cannot be expressed as a linear function of \(\textbf{u}_{\sigma }=\int \textbf{v}f_{\sigma }d^{3}\textbf{v}\), where \(\gamma =\left( 1-v^{2}/c^{2}\right) ^{-1/2}\). The relativistic Vlasov equation reads, in space vs. momentum space,
for which the first moment in \(\textbf{p}\) can be taken and then the curl to obtain the relativistic equivalent of Eq. 6. If \(\partial /\partial z\rightarrow 0\) is assumed, the z-component becomes
where \(\left[ A,B\right] =\hat{z}\cdot \nabla A\times \nabla B\) is the Poisson bracket. Therefore, relativistic effects add an additional source term for canonical vorticity, the role of which will be investigated in the future. There are previous efforts regarding including relativistic effects [9, 28], but the full pressure tensor have not been considered.
So far, only the electron canonical vorticity was examined. However, Eq. 6 is valid for any species, in particular for ions. Therefore, there should be an ion canonical battery effect in analogy to the electron canonical battery effect. Whether and when this effect becomes important will be a good future investigation.
The framework presented here assumes no collisions between particles. If collisions are assumed and a term \(m_\sigma \nu _{\sigma \mu }\left( \textbf{u}_\mu -\textbf{u}_\sigma \right)\) is added to the right-hand-side of Eq. 2, then Eq. 6 becomes
where \(\nu _{\mu \sigma }\) is the collision frequency between species \(\sigma\) and \(\mu\), and \(\boldsymbol{\Omega }_\mu\) is the vorticity of species \(\mu\). The vorticities form part of the canonical vorticities of each species, and the role of these collision terms will be investigated in the future.
6 Conclusion
The canonical vorticity theoretical framework, which takes the canonical vorticity as the main variable instead of the magnetic field, provides intuitive, simplified explanations for various magnetized plasma phenomena. Magnetic reconnection and magnetogenesis were presented as two of the example in which this framework serves as a simplifier. Some suggestions for future work were also given, namely the extension of this framework in the relativistic regime and in a regime with multiple significant species.
Data availibility
Relevant materials may be obtained from the author upon reasonable request.
References
-
M. Yamada, R. Kulsrud, H. Ji, Magnetic reconnection. Rev. Mod. Phys. 82, 603–664 (2010). https://doi.org/10.1103/RevModPhys.82.603
-
H. Ji, W. Daughton, J. Jara-Almonte, A. Le, A. Stanier, J. Yoo, Magnetic reconnection in the era of exascale computing and multiscale experiments. Nat. Rev. Phys. 4, 263–282 (2022). https://doi.org/10.1038/s42254-021-00419-x
-
M. Hirota, P. Morrison, Y. Ishii, M. Yagi, N. Aiba, Nonlinear variational method for predicting fast collisionless magnetic reconnection. Nucl. Fusion 53, 063024 (2013). https://doi.org/10.1088/0029-5515/53/6/063024
-
M. Hirota, Y. Hattori, P.J. Morrison, Explosive magnetic reconnection caused by an x-shaped current-vortex layer in a collisionless plasma. Phys. Plasmas 22, (2015). https://doi.org/10.1063/1.4921329
-
L. Turner, Hall effects on magnetic relaxation. IEEE Trans. Plasma Sci. 14, 849–857 (1986). https://doi.org/10.1109/TPS.1986.4316633
-
A. Kingsep, Reviews of Plasma Physics, vol. 16 (Consultants Bureau, New York, 1990)
-
A.V. Gordeev, A.S. Kingsep, L.I. Rudakov, Electron magnetohydrodynamics. Phys. Rep. 243, 215–315 (1994). https://doi.org/10.1016/0370-1573(94)90097-3
-
L.C. Steinhauer, A. Ishida, Relaxation of a two-specie magnetofluid. Phys. Rev. Lett. 79, 3423–3426 (1997). https://doi.org/10.1103/PhysRevLett.79.3423
-
S.M. Mahajan, Temperature-transformed “minimal coupling’’: Magnetofluid unification. Phys. Rev. Lett. 90, 035001 (2003). https://doi.org/10.1103/PhysRevLett.90.035001
-
S. You, A field theory approach to the evolution of canonical helicity and energy. Phys. Plasmas 23, 072108 (2016). https://doi.org/10.1063/1.4956465
-
P.M. Bellan, Magnetic Helicity, Spheromaks, Solar Corona Loops, and Astrophysical Jets (World Scientific, Europe, 2018). https://doi.org/10.1142/q0151
-
Y.D. Yoon, P.M. Bellan, A generalized two-fluid picture of non-driven collisionless reconnection and its relation to whistler waves. Phys. Plasmas 24, 052114 (2017). https://doi.org/10.1063/1.4982812
-
Y.D. Yoon, P.M. Bellan, An intuitive two-fluid picture of spontaneous 2d collisionless magnetic reconnection and whistler wave generation. Phys. Plasmas 25, 055704 (2018). https://doi.org/10.1063/1.5016345
-
Y.D. Yoon, P.M. Bellan, The electron canonical battery effect in magnetic reconnection: Completion of the electron canonical vorticity framework. Phys. Plasmas 26, 100702 (2019). https://doi.org/10.1063/1.5122225
-
E.S. Weibel, Spontaneously growing transverse waves in a plasma due to an anisotropic velocity distribution. Phys. Rev. Lett. 2, 83–84 (1959). https://doi.org/10.1103/PhysRevLett.2.83
-
L. Biermann, Über den ursprung der magnetfelder auf sternen und im interstellaren raum. Z. Naturforsch. A 5, 65–71 (1950). https://doi.org/10.1515/zna-1950-0201
-
M. Laishram, G. Yun, Y. Yoon, Magnetogenesis via the canonical battery effect. Phys. Rev. Res. 6, (2024). https://doi.org/10.1103/PhysRevResearch.6.L032052
-
J. Birn, J.F. Drake, M.A. Shay, B.N. Rogers, R.E. Denton, M. Hesse, M. Kuznetsova, Z.W. Ma, A. Bhattacharjee, A. Otto, P.L. Pritchett, Geospace environmental modeling (gem) magnetic reconnection challenge. J. Geophys. Res. Space Phys. 106, 3715–3719 (2001). https://doi.org/10.1029/1999ja900449
-
E. Cafaro, D. Grasso, F. Pegoraro, F. Porcelli, A. Saluzzi, Invariants and geometric structures in nonlinear hamiltonian magnetic reconnection. Phys. Rev. Lett. 80, 4430–4433 (1998). https://doi.org/10.1103/PhysRevLett.80.4430
-
Y.D. Yoon, P.M. Bellan, Fast ion heating in transient collisionless magnetic reconnection via an intrinsic stochastic mechanism. Astrophys. J. Lett. 868, L31 (2018). https://doi.org/10.3847/2041-8213/aaf0a3
-
J.M. McChesney, R.A. Stern, P.M. Bellan, Observation of fast stochastic ion heating by drift waves. Phys. Rev. Lett. 59, 1436–1439 (1987). https://doi.org/10.1103/PhysRevLett.59.1436
-
K. Stasiewicz, R. Lundin, G. Marklund, Stochastic ion heating by orbit chaotization on electrostatic waves and nonlinear structures. Phys. Scr. T 84, 60–63 (2000). https://doi.org/10.1238/physica.topical.084a00060
-
Y.D. Yoon, P.M. Bellan, Kinetic verification of the stochastic ion heating mechanism in collisionless magnetic reconnection. Astrophys. J. Lett. 887, L29 (2019). https://doi.org/10.3847/2041-8213/ab5b0a
-
Y.D. Yoon, P.M. Bellan, How hall electric fields intrinsically chaotize and heat ions during collisionless magnetic reconnection. Phys. Plasmas 28, 022113 (2021). https://doi.org/10.1063/5.0040374
-
Y. Yoon, P. Bellan, G. Yun, Phase-space analysis of ordered and disordered nonthermal ion energization during magnetic reconnection. Astrophys. J. 956, (2023). https://doi.org/10.3847/1538-4357/acf1f5
-
K.M. Schoeffler, N.F. Loureiro, R.A. Fonseca, L.O. Silva, Magnetic-field generation and amplification in an expanding plasma. Phys. Rev. Lett. 112, 175001 (2014). https://doi.org/10.1103/PhysRevLett.112.175001
-
A. Le, J. Egedal, O. Ohia, W. Daughton, H. Karimabadi, V.S. Lukin, Regimes of the electron diffusion region in magnetic reconnection. Phys. Rev. Lett. 110, 135004 (2013). https://doi.org/10.1103/PhysRevLett.110.135004
-
Y. Kawazura, Z. Yoshida, Y. Fukumoto, Relabeling symmetry in relativistic fluids and plasmas (2014). https://doi.org/10.1088/1751-8113/47/46/465501
Acknowledgements
The authors thanks Paul M. Bellan, Gunsu S. Yun, and Modhuchandra Laishram for their historical contributions towards the present work.
Funding
This work was supported by an appointment to the JRG Program at the APCTP through the Science and Technology Promotion Fund and Lottery Fund of the Korean government, and also by the Korean Local Governments-Gyeongsangbuk-do Province and Pohang City.
Author information
Authors and Affiliations
Contributions
Y. D. Yoon supervised the project and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The author declares no competing interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.