1 Introduction

Topological and geometric aspects of electronic Bloch wavefunctions in the Brillouin zone (BZ), including the Berry curvature [1,2,3] and quantum metric [3,4,5,6], play essential roles in our understanding of physical responses in crystalline materials. For example, the Hall conductivity of a 2D crystalline insulator can be related to the integral of the momentum-space Berry curvature for the Bloch wavefunctions over the entire BZ, which is identified as a topological index called the “Chern number” in the formula first derived by Thouless, Kohmoto, Nightingale, and den Nijs [7]. The Berry curvature integral of the occupied states, which is not quantized, also provides an intrinsic mechanism for the anomalous Hall effect in a variety of ferromagnetic metals. More recently, physical phenomena induced by non-linear responses have also been connected to band topology or geometry. For example, the Berry curvature dipole and quantum metric dipole are theoretically proposed to be the origin of the non-linear Hall effect in non-magnetic or anti-ferromagnetic materials, which preserve either time-reversal symmetry (\(\hat{T}\)) or the combined \(\hat{P}\hat{T}\)-symmetry where \(\hat{P}\) is inversion [8,9,10,11,12,13]. This geometric origin of non-linear Hall effect has been experimentally demonstrated in a variety of material compounds [14,15,16,17,18,19,20,21,22,23,24,25]. Quantized topological non-linear response due to chiral charges of Weyl nodes has also been theoretically proposed for the circular photogalvanic effect (CPGE) in Weyl semimetals [26,27,28]. Experimental observation of CPGE has been reported in chiral multifold semimetals RhSi and CoSi and its connection to topological chiral charges has been discussed [29,30,31].

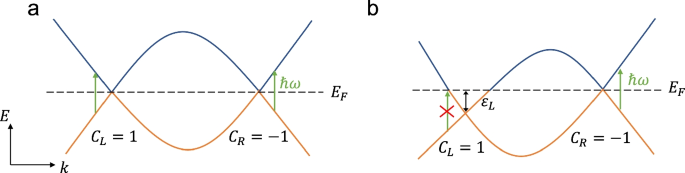
The CPGE is a second-order optical response, in which the current switches its direction when the circularly polarized incident light changes its polarization [27,28,29,30,31,32,33,34]. In Ref. [27], de Juan et al. proposed that the CPGE can be quantized in the Weyl semimetal phase of chiral crystals and this quantization originates from the topological chiral charge of Weyl nodes. Because the Weyl nodes must appear in pairs with opposite chiral charges in crystals, the CPGE contributions from the Weyl nodes with opposite chiral charges will cancel each other, generally leading to the vanishing CPGE (Fig. 1a). To overcome this obstruction, it was theoretically proposed that when two Weyl nodes with opposite chiral charges sit at different energies and the Fermi energy is close to one Weyl node but far away from the other Weyl node (Fig. 1b), optical inter-band transitions can only occur for the Weyl fermion close to the Fermi energy but not for the other due to Pauli blocking [27]. This scenario can occur in the Weyl semimetal phase of chiral crystals, in which the inversion and all the mirror symmetries are broken, so that no symmetry can connect the Weyl nodes with opposite chiral charges, and thus they can appear at different energies. We note that time-reversal symmetry can only relate two Weyl nodes with the same chiral charge. However, experimental confirmation of quantized CPGE is still lacking, and it was suggested that additional contributions from remote bands, rather than the two bands that form Weyl fermions, can have a significant contribution to the CPGE, which can be much larger than the quantized contribution in realistic materials [35]. Furthermore, it was also suggested that interactions and disorders can destroy the quantization of CPGE in chiral Weyl semimetals [36, 37].

Fig. 1
figure 1

a Schematic of the energy dispersion for a two-band Weyl semimetal that preserves mirror symmetry and breaks time-reversal symmetry. The left and right Weyl nodes have opposite C and sit at the same energy. The current response of topological CPGE will cancel out between these two Weyl nodes due to the opposite chiral charges, but the magnetic-resonance-induced non-linear current proposed in this work will remain. b Band structure of a chiral Weyl semimetal where the two Weyl nodes are at different energies. The topological CPGE can exist due to Pauli blocking


In this work, we propose an alternative approach to overcome this obstruction in magnetic Weyl semimetals, in which time-reversal symmetry is broken but inversion symmetry is preserved. The current response from the second order (or any even order) of electric fields (\(E^2\)) necessarily requires inversion symmetry breaking, which directly follows from the fact that both current and electric field are odd under inversion. Following this argument, the CPGE contributions from different Weyl nodes in centrosymmetric magnetic Weyl semimetals will cancel each other so that we expect a vanishing CPGE for the second-order response (Fig. 1a). The key idea in our approach is to replace one electric field E with magnetization M, which is even under inversion. Therefore, the second-order current response with respect to one magnetization M and one electric field E is allowed to exist in centrosymmetric magnetic Weyl semimetals from the symmetry view. Microscopically, to understand how magnetization dynamics affects the inter-band transition of Weyl fermions, we introduce the concept of “pseudo-gauge field" in magnetic Weyl semimetals and show that magnetic fluctuations (or spin wave) can play the role of a pseudo-gauge field[38,39,40]. Here the pseudo-gauge field refers to the perturbation that behaves in a similar manner as a gauge field coupled to the Weyl fermions in the low-energy sector of the system. Unlike the usual electromagnetic field, this gauge coupling depends on the chirality of Weyl fermions and has opposite signs when the Weyl fermion chirality reverses. In Section 3, we will study the non-linear current response in magnetic Weyl semimetals due to the interplay between electromagnetic fields and the magnetic-resonance (MR) induced pseudo-gauge field, in analogy to the CPGE purely from the electromagnetic fields. Strikingly, we find that two Weyl nodes with opposite chiral charges contribute with the same sign to the MR-induced nonlinear current, in sharp contrast to the opposite sign contributions of the normal CPGE. This difference originates from the chirality-dependent gauge coupling form of the pseudo-gauge field. In Section 4, we will demonstrate that the magnetic fluctuation or spin wave, which can be driven via ferromagnetic resonance, serves as the pseudo-gauge field in magnetic Weyl semimetals. In Section 5, we implemented numerical studies of the magnetic-resonance-induced nonlinear current response in a magnetic Weyl semimetal model that was previously adopted to describe magnetically doped topological insulators, in order to justify our analytical solutions.

2 Model Hamiltonian

We start from a four-band model that describe a topological insulator system with ferromagnetism in Ref. [41], which can capture the Weyl semimetal phase when magnetization term dominates over the non-magnetic band gap. The model Hamiltonian reads

\(\begin{aligned}&H = H_0 +H_1, \nonumber \\&H_0 = {\mathcal {M}}(\boldsymbol{k}) \tau _z + L_1 k_z \tau _y + L_2 (k_y \sigma _x - k_x \sigma _y) \tau _x + m \sigma _z, \nonumber \\&H_1 = \boldsymbol{\nu } (t) \cdot \boldsymbol{\sigma } \tau _z, \end{aligned}\)
(1)

where \({\mathcal {M}}(\boldsymbol{k}) = M_0 + M_1 k^2_z + M_2 (k^2_x + k^2_y)\), \(M_{0,1,2}, L_{1,2}\) are material dependent parameters, and m describes the out-of-plane magnetization and can induce the Weyl semimetal phase when \(m>M_0\) after neglecting the quadratic terms in \({\mathcal {M}}(\boldsymbol{k})\). Here we also include the \(H_1\) term that represents the magnetic fluctuation, which preserves the inversion symmetry \(\tau _z\) and breaks the time-reversal \(i\sigma _y K\) (K is the complex conjugate operator), and assume \(\boldsymbol{\nu } (t)\) has temporal dependence. In Ref. [41], additional terms with the form \(\boldsymbol{\mu } (t) \cdot \boldsymbol{\sigma }\) can exist for magnetic fluctuations. However, these terms will only slightly modify the form of the pseudo-gauge field discussed below and does not affect the final result. Thus, we drop these additional terms and only focus on the \(\boldsymbol{\nu } (t)\) terms in this work. \(H_1\) is treated as a perturbation below. Next we will show that when the model Hamiltonian is in the magnetic Weyl semimetal phase for \(m>M_0\) and projected to the subspace of two low-energy Weyl fermions, the magnetic fluctuation in \(H_1\) acts like a chiral gauge field which couples oppositely to the Weyl fermions with left and right chiralities [41].

The eigen-energy of the Hamiltonian \(H_0\) in Eq. (1) can be solved analytically as

\(\begin{aligned} \varepsilon _{\lambda \mu } = \lambda \sqrt{L_2^2 \left( k_x^2 + k_y^2 \right) + \left( \sqrt{{\mathcal {M}}^2 + L_1^2 k_z^2} + \mu \left| m\right| \right) ^2}, \end{aligned}\)
(2)

where \(\lambda , \mu = \pm\), and we denote the eigenstates as \(\left| \lambda ,\mu \right\rangle\). When \(k_x = k_y = 0\), the eigen-energies of the two middle bands are \(\varepsilon _{-,-} = - \sqrt{{\mathcal {M}}^2 + L_1^2 k_z^2} +m\) and \(\varepsilon _{+,-} = \sqrt{{\mathcal {M}}^2 + L_1^2 k_z^2} -m\), assuming \(m> 0\). Thus, the gap between the two states \(\left| -,-\right\rangle\) and \(\left| +,-\right\rangle\) can be closed at \({\mathcal {M}}^2 + L_1^2 k_z^2 = m^2\) if \(m> \left| {\mathcal {M}}\right|\). By neglecting the quadratic term \(M_1 k_z^2\) in \({\mathcal {M}}(\boldsymbol{k})\), namely \({\mathcal {M}}(\boldsymbol{k})=M_0\), we can find two gap closing points at \(\boldsymbol{k}=(0, 0, \pm K_0)\) with \(K_0 = \sqrt{m^2 - M_0^2}/L_1\).

At the gap closing point \(\boldsymbol{k}_0 = (0, 0, K_0)\), the Hamiltonian can be simplified as

\(\begin{aligned} H_0 (\boldsymbol{k}_0) = M_0 \tau _z + L_1 K_0 \tau _y +m \sigma _z, \end{aligned}\)
(3)

and the eigenstates are solved as

\(\begin{aligned}&\left| -,+\right\rangle = \frac{1}{\sqrt{N_-}} \left( \begin{array}{c} 0 \\ 0 \\ M_0 - m \\ i L_1 K_0 \end{array}\right) ,\quad \left| -,-\right\rangle = \frac{1}{\sqrt{N_-}} \left( \begin{array}{c} M_0 - m \\ i L_1 K_0 \\ 0 \\ 0 \end{array}\right) ,\nonumber \\&\left| +,-\right\rangle = \frac{1}{\sqrt{N_+}} \left( \begin{array}{c} 0 \\ 0 \\ M_0 + m \\ i L_1 K_0 \end{array}\right) ,\quad \left| +,+\right\rangle = \frac{1}{\sqrt{N_+}} \left( \begin{array}{c} M_0 + m \\ i L_1 K_0 \\ 0 \\ 0 \end{array}\right) , \end{aligned}\)
(4)

where \(N_\pm = (M_0 \pm m)^2 + L_1^2 K_0^2\) are the normalization factors. The effective Hamiltonian around \(\boldsymbol{k}_0\) up to the first order in \(\delta \boldsymbol{k}\) is written as

\(\begin{aligned} H' = L_1 \delta k_z \tau _y + L_2 (\delta k_y \sigma _x - \delta k_x \sigma _y) \tau _x + \boldsymbol{\nu } \cdot \boldsymbol{\sigma } \tau _z. \end{aligned}\)
(5)

We then project the effective Hamiltonian \(H'\) into the subspace of the basis \(\left| -,-\right\rangle\) and \(\left| +,-\right\rangle\) by applying the second-order perturbation

\(\begin{aligned} H_{mn} = \left\langle m\right| H' \left| n\right\rangle + \sum _{l \ne m,n} \frac{1}{2}\left\langle m\right| H' \left| l\right\rangle \left\langle l\right| H' \left| n\right\rangle \times \left[ \frac{1}{\varepsilon _m - \varepsilon _l} +\frac{1}{\varepsilon _n - \varepsilon _l} \right] . \end{aligned}\)
(6)

By keeping \(\delta \boldsymbol{k}\) up to the first order and \(\boldsymbol{\nu }\) up to the second order, we can then write down the low-energy effective Hamiltonian for the two gap closing points at \((0,0,K_0)\) and \((0,0,-K_0)\) as

\(\begin{aligned} H_{eff}&= \left( L_2 \delta k_x \tau _z + \frac{L_1 K_0}{m} \nu _x\right) \sigma _x + \left( L_2 \delta k_y \tau _z+ \frac{L_1 K_0}{m} \nu _y\right) \sigma _y \nonumber \\&\quad + \frac{1}{2m}\left( 2L_1^2 K_0 \delta k_z \tau _z - \nu _z^2 + \frac{M_0^2}{m^2} (\nu _x^2+\nu _y^2+\nu _z^2)\right) \sigma _z \nonumber \\&= \hbar v_f \boldsymbol{\sigma } \cdot \left( \delta \boldsymbol{k}\, \tau _z + \frac{e}{\hbar } \boldsymbol{a}\right) , \end{aligned}\)
(7)

where \(\boldsymbol{\sigma }\) are Pauli matrices in the spin basis, \(\tau _z\) is in the basis of two Weyl points, \(\hbar v_f = L_2\), \(\delta \boldsymbol{k}= (\delta k_x, \delta k_y, \frac{L_1^2 K_0}{L_2 m}\delta k_z)\), and \(\boldsymbol{a} = (a_x, a_y, a_z)\) with \(a_x = \frac{\hbar L_1 K_0}{e L_2 m} \nu _x\), \(a_y = \frac{\hbar L_1 K_0}{e L_2 m} \nu _y\), and \(a_z = \frac{\hbar }{2 e L_2 m}(- \nu _z^2 + \frac{M_0^2}{m^2} (\nu _x^2+\nu _y^2+\nu _z^2))\). We may introduce the electromagnetic field by the Peierls substitution \(\delta \boldsymbol{k}\rightarrow \delta \boldsymbol{k}+ \frac{e}{\hbar } \boldsymbol{A}\) with the vector potential \(\boldsymbol{A}\). By comparing the coupling form of \(\boldsymbol{A}\) with \(\boldsymbol{a}\), we find that the \(\boldsymbol{a}\) field, which results from the magnetic fluctuation \(\boldsymbol{\nu }\), couples oppositely to the Weyl nodes at the two gap closing points in a gauge coupling form, and thus we conclude the \(\boldsymbol{a}\) field acts like a chiral gauge field [41]. Below we will use the terminology, either chiral gauge field or pseudo-gauge field, to refer to the \(\boldsymbol{a}\) field.

Due to the presence of magnetic ordering, time-reversal symmetry is broken in magnetic Weyl semimetals, and the minimal model of Weyl semimetals with two Weyl nodes can be realized by the model Hamiltonian in Eq. (1), as shown by the numerical simulations of the energy bands for Eq. (1) in Fig. 2a. On the other hand, if only inversion symmetry is broken, the total number of Weyl nodes in the system must be a multiple of four, as time-reversal symmetry transforms a Weyl node at \(\boldsymbol{k}\) to another Weyl node at \(-\boldsymbol{k}\) with the same chirality and all the chiral charges for the whole Weyl semimetals must cancel [42].

Fig. 2
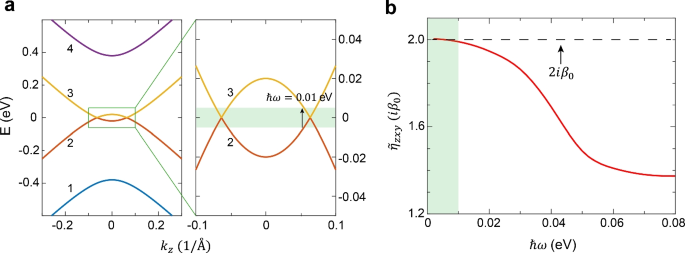
figure 2

a Energy dispersion of the four-band model along \(k_z\) at \(k_x = k_y = 0\) and the enlarged area around the two Weyl nodes. b The MR-induced non-linear current component \(\tilde{\eta }_{zxy}\) as a function of \(\hbar \omega\). The quantized value is \(2i \beta _0\), which can be achieved for \(\hbar \omega < 0.01\) eV. The parameters are chosen as \(M_0 = 0.18\) eV, \(M_1 = 0.342\) eVÅ\(^2\), \(M_2 = 18.25\) eVÅ\(^2\), \(L_1 = 1.33\) eVÅ, \(L_2 = 2.82\) eVÅ, and \(m = 0.2\) eV (parameters from Ref. [41])


3 Magnetic-resonance-induced current response for Weyl fermions

We next consider the non-linear response for the left-handed and right-handed Weyl fermions described by the Hamiltonian based on the effective Hamiltonian Eq. (7) which is rewritten as

\(\begin{aligned}&H_L = \hbar v_f \boldsymbol{\sigma } \cdot \left( \boldsymbol{k}+ \frac{e}{\hbar } \boldsymbol{A}+ \frac{e}{\hbar }\boldsymbol{a}\right) ,\nonumber \\&H_R = -\hbar v_f \boldsymbol{\sigma } \cdot \left( \boldsymbol{k}+ \frac{e}{\hbar } \boldsymbol{A}-\frac{e}{\hbar } \boldsymbol{a}\right) , \end{aligned}\)
(8)

where \(\boldsymbol{\sigma }\) is Pauli matrices, \(\boldsymbol{A}\) is the electromagnetic field, and \(\boldsymbol{a}\) is the chiral gauge field minimally coupled to the left-handed and right-handed Weyl fermions [41]. We further rewrite the above Hamiltonian as

\(\begin{aligned} H_L&= H_{L0} + \boldsymbol{A}\cdot \boldsymbol{J}_L + \boldsymbol{a}\cdot \boldsymbol{J}_L,\nonumber \\ H_R&= H_{R0} + \boldsymbol{A}\cdot \boldsymbol{J}_R - \boldsymbol{a}\cdot \boldsymbol{J}_R, \end{aligned}\)
(9)

where \(H_{L0} =-H_{R0} = \hbar v_f \boldsymbol{\sigma } \cdot \boldsymbol{k}\) and \(\boldsymbol{J}_L = - \boldsymbol{J}_R = ev_f \boldsymbol{\sigma }\). Let us first focus on the left-handed Weyl fermion \(H_L\). Following the density matrix formalism in the velocity gauge described in Appendix 2, we rewrite the Hamiltonian into the second-quantization form as

\(\begin{aligned} \hat{H}_L = \sum _n \int d\boldsymbol{k}\varepsilon ^L_{n\boldsymbol{k}} \hat{a}^{\dagger }_{n\boldsymbol{k}} \hat{a}_{n\boldsymbol{k}} +\sum _{nn'} \int d\boldsymbol{k}\hat{a}^{\dagger }_{n\boldsymbol{k}} \hat{a}_{n'\boldsymbol{k}} \left[ \boldsymbol{A}(t)\cdot \boldsymbol{J}^L_{nn'\boldsymbol{k}} + \boldsymbol{a}_L (t) \cdot \boldsymbol{J}^L_{nn'\boldsymbol{k}} \right] , \end{aligned}\)
(10)

where \(\varepsilon ^L_{n\boldsymbol{k}}\) is the eigenvalue of \(H_{L0}\) and \(\hat{a}_{n\boldsymbol{k}}\) and \(\hat{a}_{n\boldsymbol{k}}^{\dagger }\) are the annihilation and creation operators. The Bloch equation of the density matrix \(\rho _{nm}(t)\), defined by \(\rho _{nm,\boldsymbol{k}} (t) = \langle \hat{a}_{m\boldsymbol{k}}^{\dagger }(t) \hat{a}_{n\boldsymbol{k}} (t) \rangle\), is then

\(\begin{aligned} \frac{\partial \rho _{nm}(t)}{\partial t} = -\frac{i}{\hbar } \varepsilon ^L_{nm} \rho _{nm}(t) - \frac{i}{\hbar } \sum _{n'} \left[ \boldsymbol{A}(t) \cdot \boldsymbol{J}^L_{n'n} \rho _{n'm}(t) - \boldsymbol{A}(t) \cdot \boldsymbol{J}^L_{mn'} \rho _{nn'}(t) \right] \nonumber \\ - \frac{i}{\hbar } \sum _{n'} \left[ \boldsymbol{a}_L(t) \cdot \boldsymbol{J}^L_{n'n} \rho _{n'm}(t) - \boldsymbol{a}_L(t) \cdot \boldsymbol{J}^L_{mn'} \rho _{nn'}(t) \right] - \frac{\rho _{nm}(t)}{\tau }, \end{aligned}\)
(11)

where \(\tau\) is the relaxation time and \(\varepsilon ^L_{nm} = \varepsilon ^L_n - \varepsilon ^L_m\). We can expand the density matrix in order of the perturbation of dynamic fields \(\boldsymbol{A}\) and \(\boldsymbol{a}\). The zeroth order of the density matrix is given by \(\rho ^{(0)}_{nm} = f_n \delta _{nm}\) where \(f_n\) is the Fermi factor of band n. At the first order of \(\boldsymbol{A}\) and \(\boldsymbol{a}\), we obtain

\(\begin{aligned} \rho ^{(1)}_{nm} (\omega ) =f_{nm} \frac{ \left( A^b (\omega ) + a^b_L (\omega ) \right) (J_L)^b_{mn}}{\hbar (\tilde{\omega }_{1,nm} - \omega )}, \end{aligned}\)
(12)

where we define \(f_{nm} = f_n - f_m\), \(A^b (t) = A^b (\omega ) e^{-i\omega t}\), \(a_L^b (t) = a_L^b (\omega ) e^{-i\omega t}\), and \(\tilde{\omega }_{1,nm} =\varepsilon ^L_{nm}/\hbar - i/\tau\). Here the Einstein summation rule has been assumed. At the second order of \(\boldsymbol{A}\) and \(\boldsymbol{a}\), the diagonal component of density matrix can be derived as

\(\begin{aligned} \rho ^{(2)}_{nn} (\omega _{\Sigma }) = \frac{1}{\hbar \omega _{\Sigma }}\sum _m \left( A^b_{\beta } (a_L)^c_{\gamma } + (a_L)^b_{\beta } A^c_{\gamma } \right) \left[ \frac{f_{mn}(J_L)^b_{mn} (J_L)^c_{nm} }{\hbar (\tilde{\omega }_{1,mn} - \omega _{\beta })} - \frac{f_{nm}(J_L)^b_{nm} (J_L)^c_{mn} }{\hbar (\tilde{\omega }_{1,nm} - \omega _{\beta })} \right] , \end{aligned}\)
(13)

where \(\omega _{\Sigma } = \omega _{\beta } + \omega _{\gamma }\), \(A^b_{\beta } = A^b(\omega _{\beta })\), and \((a_L)^b_{\beta } = (a_L)^b (\omega _{\beta })\). Here we only consider the diagonal term in the second order of density matrix \(\rho ^{(2)}\). This is because we only consider two bands that form the Weyl points here, and the off-diagonal component of \(\rho ^{(2)}\) is zero. It should be noted that if the third bands are involved, the off-diagonal component of \(\rho ^{(2)}\) can exist and a three-band contribution can be important for the CPGE [35]. Moreover, we only keep the terms involving both \(\boldsymbol{A}\) and \(\boldsymbol{a}_L\), as the other terms quadratic in \(\boldsymbol{A}\) or \(\boldsymbol{a}_L\) vanish between the left-handed and right-handed Weyl fermions due to their opposite chiral charges (see Appendix 1). The corresponding intraband current is derived as

\(\begin{aligned} \tilde{j}_L^a (t)&= e \sum _n \int _k v^a_{nn} \rho ^{(2)}_{nn} (\omega _{\Sigma }) e^{-i\omega _{\Sigma } t} \nonumber \\&=\frac{e}{\hbar ^2 \omega _{\Sigma }}\sum _{nm} \int _k \frac{\Delta ^a_{nm} f_{mn}(J_L)^b_{mn} (J_L)^c_{nm} }{\tilde{\omega }_{1,mn} - \omega _{\beta }} \left( A^b_{\beta } (a_L)^c_{\gamma } + (a_L)^b_{\beta } A^c_{\gamma } \right) e^{-i\omega _{\Sigma } t}, \end{aligned}\)
(14)

where \(v^a_{nm} = \left\langle n\right| \frac{\partial H}{\partial k_a} \left| m\right\rangle\) is the matrix element of the velocity operator and \(\Delta ^a_{nm} = v^a_{nn} - v^a_{mm}\) is the velocity shift. We then use \(A^b (\omega ) = E^b(\omega )/i\omega\), \(a_L^b (\omega )= \tilde{E}^b (\omega )/i\omega\) with the pseudo-electric field \(\tilde{E}\), and \((J_L)^b_{nm} = \frac{ie}{\hbar }\varepsilon ^L_{nm} {\mathcal {A}}^b_{nm}\) with the Berry connection \(\boldsymbol{{\mathcal {A}}}_{nm} = \left\langle n\right| i\partial _{\boldsymbol{k}} \left| m\right\rangle\). We symmetrize all the indices, and take the time derivative of the imaginary part (see Appendix 1) to obtain

\(\begin{aligned} \frac{d \tilde{j}^a_L (t)}{dt} = \tilde{\eta }^L_{abc} (\omega _{\Sigma };\omega _{\beta }, \omega _{\gamma }) E^b_{\beta } \tilde{E}^c_{\gamma } e^{-i\omega _{\Sigma } t} + \tilde{\eta }^L_{abc} (\omega _{\Sigma };\omega _{\gamma }, \omega _{\beta }) \tilde{E}^b_{\beta } E^c_{\gamma } e^{-i\omega _{\Sigma } t}, \end{aligned}\)
(15)

where

\(\begin{aligned} \tilde{\eta }^L_{abc} (\omega _{\Sigma };\omega _{\beta }, \omega _{\gamma })&= -\frac{i \pi e^3}{8\hbar ^2} \sum _{nm} \int _k \Delta ^a_{nm} f_{nm} (\Omega _L)^{bc}_{mn} \frac{\varepsilon ^2_{nm}}{\hbar ^2 \omega _{\beta } \omega _{\gamma }} \nonumber \\&\quad \times \left[ \delta (\omega _{mn} - \omega _{\beta }) - \delta (\omega _{mn} + \omega _{\beta }) - \delta (\omega _{mn} - \omega _{\gamma }) + \delta (\omega _{mn} + \omega _{\gamma }) \right] , \end{aligned}\)
(16)

with the Berry curvature of the left-handed Weyl fermion \((\Omega _L)^{bc}_{mn} = i({\mathcal {A}}^b_{mn}{\mathcal {A}}^c_{nm} - {\mathcal {A}}^c_{mn}{\mathcal {A}}^b_{nm})\). For \(\omega _{\beta } = -\omega _{\gamma } = \omega\) and \(\omega _{\Sigma } = 0\), we have

\(\begin{aligned} \tilde{\eta }^L_{abc}(0; \omega ,-\omega ) = -\frac{i \pi e^3}{2\hbar ^2} \sum _{nm} \int _k \Delta ^a_{nm} f_{nm} (\Omega _L)^{bc}_{mn} \delta (\omega _{mn} - \omega ). \end{aligned}\)
(17)

We rewrite the above equations as (see Appendix 1)

\(\begin{aligned} \tilde{\boldsymbol{j}}_L = \tau \tilde{\beta }_L (\omega ) \left[ \boldsymbol{E}(\omega ) \times \tilde{\boldsymbol{E}}^* (\omega ) +\tilde{\boldsymbol{E}}(\omega ) \times \boldsymbol{E}^* (\omega )\right] , \end{aligned}\)
(18)

where \(\tilde{\boldsymbol{E}} (\omega ) = i\omega \boldsymbol{a}\) can be regarded as the pseudo-electric field, and the MR-induced current response trace for the left-handed Weyl fermion is

\(\begin{aligned} \tilde{\beta }_L (\omega ) = i\frac{e^3}{2h^2} \oint d\boldsymbol{S} \cdot \boldsymbol{\Omega }_L = i\beta _0 C_L, \end{aligned}\)
(19)

where \(\boldsymbol{S}\) is a closed surface in the momentum space, \(\beta _0 = \pi e^3/h^2\), and \(C_L = \frac{1}{2\pi } \oint d\boldsymbol{S} \cdot \boldsymbol{\Omega }_L = 1\) is nothing but the Chern number (equivalently the chiral charge of the Weyl node). For the right-handed Weyl fermion with \(C_R = -C_L\), we repeat the above derivation to obtain \(\tilde{\boldsymbol{j}}_R = \tilde{\boldsymbol{j}}_L\). Thus, the total non-linear response current is

\(\begin{aligned} \tilde{\boldsymbol{j}}&= \tilde{\boldsymbol{j}}_L + \tilde{\boldsymbol{j}}_R = 2i \tau \beta _0 C_L \left[ \boldsymbol{E}(\omega ) \times \tilde{\boldsymbol{E}}^* (\omega ) +\tilde{\boldsymbol{E}}(\omega ) \times \boldsymbol{E}^* (\omega )\right] . \end{aligned}\)
(20)

The current Eq. (20) is the main result of this work, from which we demonstrate that a non-zero total dc-current can be induced by the interplay between an electromagnetic field and a chiral gauge field at the non-linear order for two Weyl nodes with opposite chiral charges, in contrast to the regular CPGE as discussed in Appendix 1 (also see Ref. [27]). Furthermore, the symmetry properties of each component in Eq. (20) are summarized in Table 1. Unlike the physical electric field E, the pseudo-electric field \(\tilde{E}\) is even under inversion. Therefore, this current response is allowed in centrosymmetric systems, i.e., when the inversion symmetry is preserved. From Eq. (7), we can see that the chiral gauge field \(\boldsymbol{a}\) depends on the time-dependent field \(\boldsymbol{\nu } (t)\) that describes magnetic fluctuations and thus we study the magnetic dynamics in magnetic topological insulators below.

Table 1 Symmetry properties of current \(\tilde{j}\), relaxation time \(\tau\), electric field E, and pseudo-electric field \(\tilde{E}\) (\(+\) for even and − for odd)<

  j ~ τ E E ~
Inversion − + − +
Time-reversal − − + +

4 Landau-Lifshitz-Gilbert equation for ferromagnetic resonance

To see how the magnetic fluctuation can induce a pseudo-electric field, we solve the Landau-Lifshitz-Gilbert (LLG) equation for ferromagnetic resonance in this section. Similar to Ref. [38], the LLG equation reads

\(\begin{aligned} \frac{d \boldsymbol{M}}{dt} = -\gamma _0 \boldsymbol{M}\times \left( \boldsymbol{B}_{\text {eff}} - \eta \frac{d \boldsymbol{M}}{dt} \right) , \end{aligned}\)
(21)

where \(\boldsymbol{M}= (M_x, M_y, M_z)\) is the magnetization. The in-plane magnetization acts as a pseudo-gauge field in terms of \(\boldsymbol{\nu } = \frac{c }{e v_f} g_M(-M_y, M_x, 0)\), with the exchange coupling coefficient \(g_M\) [38]. Therefore, the pseudo-electric field induced by the ferromagnetic resonance is

\(\begin{aligned} \tilde{\boldsymbol{E}} = -\frac{1}{c} \frac{\partial \boldsymbol{\nu }}{\partial t} = \frac{g_M}{e v_f} (\frac{d M_y}{dt}, -\frac{dM_x}{dt}, 0). \end{aligned}\)
(22)

The LLG equation can be rewritten as

\(\begin{aligned} \frac{d \boldsymbol{M}}{dt}&= -\gamma _0 \boldsymbol{M}\times \left[ \boldsymbol{B}_{\text {eff}} - \eta \left( -\gamma _0 \boldsymbol{M}\times \left( \boldsymbol{B}_{\text {eff}} - \eta \frac{d \boldsymbol{M}}{dt} \right) \right) \right] \nonumber \\&\approx -\gamma _0 \boldsymbol{M}\times \boldsymbol{B}_{\text {eff}} - \eta \gamma ^2_0 \boldsymbol{M}\times (\boldsymbol{M}\times \boldsymbol{B}_{\text {eff}}), \end{aligned}\)
(23)

where \(\boldsymbol{B}_{\text {eff}} = \boldsymbol{B}- \boldsymbol{M}_N - \frac{KM_z}{M^2_s} \hat{e}_z\), \(\boldsymbol{B}\) is the applied magnetic field, \(M_s = \left| \boldsymbol{M}\right|\), K is the anisotropy coefficient, \(\boldsymbol{M}_N = (N_x M_x, N_y M_y, N_z M_z)\) is the demagnetizing field with \(N_x, N_y = 0\) and \(N_z = 1\) as we consider a thin film perpendicular to the z direction, \(\gamma _0 = \frac{ge}{2m_e}\) is the magneto-mechanical ratio with Landé factor g, and \(\eta\) is Gilbert damping coefficient [38, 43, 44]. Let us define the dimensionless damping constant \(\alpha = \gamma _0 \eta M_s\), \(\gamma = \frac{\gamma _0}{1 + \alpha ^2}\), and the LLG equation is written as

\(\begin{aligned} \frac{d\boldsymbol{M}}{dt} = -\gamma \boldsymbol{M}\times \boldsymbol{B}_{\text {eff}} - \frac{\gamma \alpha }{M_s} \boldsymbol{M}\times (\boldsymbol{M}\times \boldsymbol{B}_{\text {eff}}). \end{aligned}\)
(24)

Since \(dM_s/dt = 0\), only the direction \(\boldsymbol{n}= \boldsymbol{M}/M_s\) is time-dependent with

\(\begin{aligned} \frac{d\boldsymbol{n}}{dt} = -\gamma \boldsymbol{n}\times \boldsymbol{B}_{\text {eff}} - \gamma \alpha \boldsymbol{n}\times (\boldsymbol{n}\times \boldsymbol{B}_{\text {eff}}). \end{aligned}\)
(25)

We assume the in-plane magnetic field and magnetization are very small, i.e. \(\left| n_x\right| \sim \left| n_y\right| \sim \left| B_x/M_s\right| \sim \left| B_y/M_s\right| \ll 1\), and at the first order of these quantities, we have

\(\begin{aligned} \left( \begin{array}{cc} \partial _t + \alpha \tilde{\omega }& \tilde{\omega }n_z \\ -\tilde{\omega }n_z & \partial _t + \alpha \tilde{\omega }\end{array}\right) \left( \begin{array}{c} n_x \\ n_y \end{array}\right) = \left( \begin{array}{cc} \gamma \alpha & \gamma n_z \\ -\gamma n_z & \gamma \alpha \end{array}\right) \left( \begin{array}{c} B_x \\ B_y \end{array}\right) , \end{aligned}\)
(26)

where \(\tilde{\omega }= \gamma n_z B_{\text {eff},z}\) and \(n_z = M_z/ M_s = \text {sgn}(M_z)\). We then consider a general in-plane magnetic field \(\boldsymbol{B}(t) = B_0 e^{i\omega t} (a,b,0)\) where a, b are two complex numbers and describe the polarization of magnetic field components of a microwave. By performing the Laplace transformation in Appendix 4, we keep the leading order \({\mathcal {O}}(\alpha ^{-1})\) in Eqs. (101) and (102) to get

\(\begin{aligned}&n_x (t) = \frac{B_0 \gamma _0}{2\alpha \omega _0} \left[ ( a_{\text {Im}} + b_{\text {Re}} n_z) \cos (\omega _0 t) + (a_{\text {Re}} - b_{\text {Im}} n_z) \sin (\omega _0 t) \right] ,\nonumber \\&n_y (t) = \frac{B_0 \gamma _0}{2\alpha \omega _0} \left[ ( b_{\text {Im}} - a_{\text {Re}} n_z) \cos (\omega _0 t) + (b_{\text {Re}} + a_{\text {Im}} n_z) \sin (\omega _0 t) \right] , \end{aligned}\)
(27)

where the ferromagnetic resonance frequency is

\(\begin{aligned} \omega _0 = \left| \tilde{\omega }\right| = \gamma B_{\text {eff},z} \end{aligned}\)
(28)

by taking the leading order \({\mathcal {O}}(\alpha ^{-1})\) in \(\omega _r\) (Eq. (104)), and Re and Im denote the real and imaginary parts of a and b, respectively. Therefore, from Eq. (22), the pseudo-electric field reads

\(\begin{aligned} \tilde{E}_x&= \frac{g_M}{e v_f} \frac{d M_y}{d t}= \frac{g_M M_s}{e v_f} \dot{n}_y = \tilde{E}_0 (b - i a n_z) e^{i\omega _0 t},\nonumber \\ \tilde{E}_y&= -\frac{g_M}{e v_f} \frac{d M_x}{d t}= - \frac{g_M M_s}{e v_f} \dot{n}_x = -\tilde{E}_0 (a + i b n_z) e^{i\omega _0 t}, \end{aligned}\)
(29)

where \(\tilde{E}_0 = g_M B_0 / (2e v_f \eta )\). Thus, an in-plane magnetic field \(\boldsymbol{B}(t) = B_0 e^{i\omega _0 t} (a,b,0)\) can induce a pseudo-electric field

\(\begin{aligned} \tilde{\boldsymbol{E}} (t) = \tilde{E}_0 e^{i\omega _0 t} (b- ia n_z, -a - i b n_z, 0), \end{aligned}\)
(30)

where \(n_z = \text {sgn}(M_z)\). Combining Eq. (30) with Eq. (20) for the non-linear current response and considering an incident light with \(\boldsymbol{E}(t) = E_0 e^{i\omega _0 t} (c, d, 0)\), we find

\(\begin{aligned} \tilde{\boldsymbol{j}}&= 2i \tau \beta _0 C_L E_0 \tilde{E}_0 \left[ (-a^* + ib^*n_z) c - (b^* + ia^*n_z) d - (-a - ibn_z) c^* + (b - ian_z) d^* \right] \hat{e}_z \nonumber \\&= - 4 \tau \beta _0 C_L E_0 \tilde{E}_0 \text {Im} \left[ (-a^* + ib^*n_z) c - (b^* + ia^*n_z) d \right] \hat{e}_z. \end{aligned}\)
(31)

Because the MR-induced non-linear current response is generated by the combination of an electromagnetic field and a pseudo-electric field, the incident light can be linearly polarized, instead of circularly polarized which is required for the regular CPGE. For example, we can choose an incident light with \(\boldsymbol{E}(t) = E_0 e^{i\omega _0 t} (1,0,0)\) and a magnetic field \(\boldsymbol{B}(t) = B_0 e^{i\omega _0 t}(0,1,0)\) to induce a pseudo-electric field \(\tilde{\boldsymbol{E}} (t) = \tilde{E}_0 e^{i\omega _0 t} (1,-i,0)\). Thus, using Eq. (31), the MR-induced nonlinear current is \(\tilde{\boldsymbol{j}} = -4\tau \beta _0 C_L E_0 \tilde{E}_0 \hat{e}_z\) assuming \(n_z = 1\). It should be noted that although the topological invariant \(C_L\) appears in this current response, the pseudo-electric field \(\tilde{E}_0\) depends on material parameters, not just the fundamental constants, and thus we regard this non-linear current response to be geometric rather than topological.


5 Magnetic-resonance-induced non-linear current response in a microscopic model

The above analytical derivation reveals the non-linear current response induced by MR, in analogy to the regular CPGE. In this section, we will further study the non-linear current response directly from numerical calculations of the Hamiltonian Eq. (1). We emphasize that the purpose of this section is to verify the analytical solutions of the nonlinear current response in the low frequency regime for a more realistic Weyl semimetal model in a certain limit. However, the parameters chosen for the calculations of this model are not realistic, so our calculations cannot be directly applied to the realistic material systems. A comment on the additional contribution to the non-linear current response from the remote bands will be provided at the end of this section.

As shown in Appendix 3, the MR-induced non-linear current in the four-band model Eq. (1) can be derived as

\(\begin{aligned} \tilde{j}_a = \tau \tilde{\eta }_{abc} (0;\omega ,-\omega ) E_b (\omega ) \tilde{E}_c^* (\omega ) + \tau \tilde{\eta }_{acb} (0;-\omega , \omega ) \tilde{E}_b (\omega ) E_c^* (\omega ), \end{aligned}\)
(32)

with

\(\begin{aligned} \tilde{\eta }_{abc} (0;\omega ,-\omega ) = i \beta _0 \sum _{nm} \int \frac{d^3 k}{2\pi } (\partial _a \varepsilon _{nm}) f_{nm} \frac{{\mathcal {A}}^b_{nm} \Gamma ^c_{mn}}{\varepsilon _{nm}} \delta (\varepsilon _{mn} - \hbar \omega ), \end{aligned}\)
(33)

where \(\beta _0 = \pi e^3/h^2\), \(\boldsymbol{{\mathcal {A}}}_{nm}\) is the non-Abelian Berry connection of the unperturbed Hamiltonian \(H_0\), \(\boldsymbol{\Gamma } = \boldsymbol{\sigma } \tau _z\), and \(\tilde{\boldsymbol{E}}(\omega ) = i\hbar \omega \boldsymbol{\nu }/e\) is the pseudo-electric field induced by the magnetic fluctuation \(\boldsymbol{\nu }\), which comes from the ferromagnetic resonance by solving the LLG equation in Section 4.

At low energy, the four-band Hamiltonian can be projected to the effective Hamiltonian describing two Weyl points, and the magnetic fluctuation \(\boldsymbol{\nu }\) appears in the form of the chiral gauge field \(\boldsymbol{a}\) (see Section 2). In this approximation, we can rewrite \(\tilde{\boldsymbol{E}} (\omega )\) as \(i\omega \boldsymbol{a}\) following the definition of Eqs. (18) and (33) becomes

\(\begin{aligned} \tilde{\eta }_{abc} (0;\omega ,-\omega ) = i \beta _0 \frac{\hbar \nu _c}{e a_c} \sum _{nm} \int \frac{d^3 k}{2\pi } (\partial _a \varepsilon _{nm}) f_{nm} \frac{{\mathcal {A}}^b_{nm} \Gamma ^c_{mn}}{\varepsilon _{nm}} \delta (\varepsilon _{mn} - \hbar \omega ), \end{aligned}\)
(34)

where the pseudo-gauge field \(\boldsymbol{a}\) in terms of \(\boldsymbol{\nu }\) is defined in Section 2. Furthermore, Eq. (32) can be recovered to Eq. (20) derived from the effective model for the two Weyl fermions by performing projection to the subspace of the two low-energy bands. This indicates that at the low-energy range, the MR-induced non-linear current trace of this microscopic model should have a quantized value of \(2i\beta _0\).

As the magnetization in our model is in the z direction, only an in-plane pseudo-electric field can be induced by the ferromagnetic resonance [38]. We assume the incident light propagates in the z direction and has in-plane electromagnetic fields, so the indices b, c can only be x or y, and \(b\ne c\) as the electric fields are along perpendicular directions in CPGE. Furthermore, the four-band model has mirror \(M_z\) symmetry which imposes constraints \(\tilde{\eta }_{xxy} = \tilde{\eta }_{xyx} = \tilde{\eta }_{yxy} = \tilde{\eta }_{yyx} = 0\), and the in-plane rotational symmetry which imposes \(\tilde{\eta }_{zxy} = -\tilde{\eta }_{zyx}\). Therefore, in the following calculations, we focus on the component \(\tilde{\eta }_{zxy}\) given by

\(\begin{aligned} \tilde{\eta }_{zxy} = i \beta _0 \frac{L_2 m}{\sqrt{m^2 - M_0^2}} \sum _{nm} \int \frac{d^3 k}{2\pi } (\partial _z \varepsilon _{nm}) f_{nm} \frac{{\mathcal {A}}^x_{nm} \Gamma ^y_{mn}}{\varepsilon _{nm}} \delta (\varepsilon _{mn} - \hbar \omega ), \end{aligned}\)
(35)

where we have used \(a_y = \frac{\hbar L_1 K_0}{e L_2 m} \nu _y\) and \(K_0 = \sqrt{m^2 - M_0^2}/L_1\) from Section 2 to derive this result.

Figure 2a shows the energy dispersion of the four-band model along \(k_z\) at \(k_x = k_y = 0\), in which four bands are labelled by the index \(n=1, ..., 4\) from low to high energies. Two Weyl nodes with opposite charges at opposite \(k_z\) are formed by two bands \(n=2\) and 3 around the energy \(\varepsilon =0\). We numerically calculate \(\tilde{\eta }_{zxy}\) as a function of \(\hbar \omega\), as shown in Fig. 2b. When \(\hbar \omega\) is smaller than 0.01 eV (green shaded area), \(\tilde{\eta }_{zxy}\) is very close to the quantized value \(2i\beta _0\), suggesting that the microscopic model can be simplified as an effective model of two Weyl fermions at the low energy range. At around \(\hbar \omega \sim 0.01\) eV, \(\tilde{\eta }_{zxy}\) starts to decrease as the effective model of two Weyl fermions is no longer applicable, and thus \(\tilde{\eta }_{zxy}\) deviates from quantization. Another reason for the rapid decrease in \(\tilde{\eta }_{zxy}\) is that the transitions around the Weyl nodes become only partially activated as \(\hbar \omega\) exceeds the energy difference between the middle two bands at \(k_z = 0\) (\(\Delta \varepsilon \sim 0.04\) eV). Eventually, \(\tilde{\eta }_{zxy}\) becomes a constant for \(\hbar \omega> 0.06\) eV. Therefore, our numerical result confirms that the MR-induced non-linear current trace between two bands of Weyl nodes can be quantized at the low energy range, where the microscopic model recovers to the effective model of two Weyl fermions, as shown in Section 2. We emphasize that the quantization of \(\tilde{\eta }_{zxy}\) does not mean that the current \(\tilde{j}\) is quantized, as the pseudo-electric field in the response Eq. (32), unlike physical electric field E, is not an externally controlled parameter and depends on specific material parameters.

In our calculation, we have only considered two-band transitions (\(2\rightarrow 3\), where 2, 3 label two bands around \(\varepsilon =0\) for two Weyl nodes) and have not included three-band virtual transitions (\(2 \rightarrow l \rightarrow 3\) where \(l=1, 4\) labels the third bands for the three-band contributions to the non-linear current response). It is known that the three-band contribution can play an important role for the CPGE when the third band l is close to the two bands that form Weyl nodes [35], and thus destroys the quantization of CPGE. Similar physics can also occur for the MR-induced non-linear current response here. The ratio between the three-band and two-band contributions can contain the energy separation ratio \(\sim \frac{\varepsilon _n - \varepsilon _m}{\varepsilon _n - \varepsilon _l}\) [35], where \(n,m = 2, 3\) and \(l=1, 4\). This ratio decays as the energy separation between the third band and two Weyl bands increases. For the chosen model parameters, a typical energy separation between two bands of Weyl nodes is around \(0.01 \sim 0.02 eV\), below which the linear dispersion of Weyl fermions remains valid. This energy scale is one order smaller than the energy separation between the third band and these two Weyl bands, which is around 0.2 eV. As long as the other bands are far away enough from the two Weyl bands, we expect that the contribution from the three-band transition provides only a small correction.

6 Conclusion and discussion

In conclusion, we demonstrate that a non-linear current response with an electric field and a MR-induced pseudo-electric field can exist in magnetic Weyl semimetals with two Weyl nodes with opposite charges, in contrast to the regular CPGE. The pseudo-electric field can be induced by the magnetic fluctuations from ferromagnetic resonance, which acts like a chiral gauge field that couples oppositely to the lefthanded and righthanded Weyl nodes. Therefore, the realization of MR-induced non-linear current does not require a chiral Weyl semimetal in which the two Weyl nodes are located at different energies. Experimentally, we can consider the electric and magnetic components of an electromagnetic wave acting on magnetic Weyl semimetals. We expect that the direct coupling between the magnetic field component of electromagnetic wave and electron spin is negligible. The role of the oscillating magnetic field here is to induce a ferromagnetic resonance, a physical phenomenon that has been well observed in experiments. Once the magnetization procession is excited in magnetic Weyl semimetals, it is the exchange coupling between magnetization and electron spin, rather than the Zeeman coupling of magnetic fields, to induce the current response. From Eq. (31), this magnetic-resonance-induced current has the magnitude of \(4\tau E_0 \tilde{E}_0\), where \(\tilde{E}_0 = g_M B_0 \gamma _0 M_s/(2 e v_f \alpha )\) is the strength of the pseudo-electric field. With typical values of parameters \(\left| g_M M_s\right|\) = 0.1 meV, \(B_0 = 10\) G, \(\gamma _0 = 1.76 \times 10^{11}\) C/kg, \(v_f = 6.5\times 10^5\) m/s, and \(\left| \alpha \right| = 10^{-5} \sim 10^{-2}\) [38], we estimate the magnitude of \(\tilde{E}_0\) to be around \(1 \sim 1000\) V/m. Taking a sample thickness of 10 nm, a width of 100 \(\mu\)m, and a typical relaxation time in Weyl semimetals \(\tau \sim 1\) ps [27], the induced current reaches \(1\sim 10^3\) nA, which is measurable in experiments. Since any current response at the second-order purely from physical electric fields (\(E^2\) order) will vanish due to the inversion symmetry, this current response from one magnetization and one electric field (EM order) becomes the dominant contribution in centrosymmetric materials.