Abstract
Perovskites are a class of semiconductors initially recognized for their exceptional efficiency in solar cell applications. Subsequent research has revealed their diverse and attractive optoelectronic properties. Over the last decades, molecule-level engineering attempts toward the original three-dimensional (“3D”) perovskites have led to the emergence of two-dimensional (“2D”) layered crystals and introduced extensive compositional, structural, and electronic tunability through the incorporation of various organic cations to form hybrid perovskite systems. Consequently, we concentrated on the theoretical investigation of innovative and complex 2D hybrid organic-inorganic perovskites using density functional theory (DFT). A DFT-based simulation protocol has been developed, enabling the efficient simulation of hybrid perovskite systems and providing accurate explanations and predictions of various experimental phenomena. This account article summarizes the recent in-depth DFT study of the structural, electronic, and spin-related properties of 2D hybrid organic-inorganic perovskites.
1 Introduction
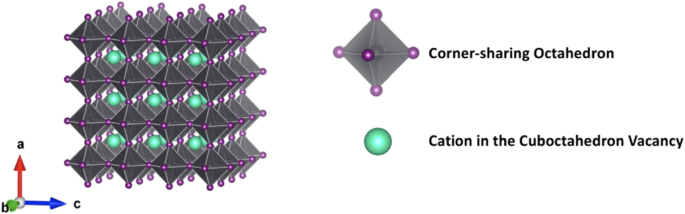
“Perovskite” originally referred to the natural mineral calcium titanate. Over time, the scope of this term expanded to encompass a diverse family of compounds sharing similar structural characteristics [1]. As shown in Fig. 1, this archetypal structure features a charge-negative framework formed by corner-sharing octahedrons [BX6], in which B is the octahedron center and the X atoms occupy the six vertices of the octahedron. Within this framework, positively charged cations A occupy the vacancies. Therefore, conventional 3D perovskites adhere to the general chemical formula ABX3.
Perovskites have long been recognized for their exceptional versatility in accommodating a diverse range of compositional and structural variations. One remarkable aspect of this adaptability lies in the flexibility of the charge-negative framework, where a diverse range of chemical elements can be incorporated. For instance, elements like Sn, Hg, and Pb can effectively undertake the role of the octahedron center (B-site) without inducing significant structural alterations, primarily due to their closely matched atomic radii and chemical valences [2]. Expanding upon this versatility, the inclusion of spin-polarized species (such as Cu) or elements with distinct chemical valences (such as Ag and Bi, which possess +1 and +3 chemical valences, respectively) within the B-site can give rise to substantial Jahn-Teller distortions, magnetic properties, and vacancy defects [3]. The X-site within perovskite structures can also accommodate a variety of elements, for example, the chlorine (Cl), bromine (Br), and iodine (I) atoms in halide perovskites. Second, the charge-negative framework of perovskites lends itself to engineering on multiple scales, spanning from the nanoscale to the atomic level. This versatility has given rise to diverse perovskite-related materials such as perovskite quantum dots, perovskite nano-surfaces, 2D perovskites, and 1D perovskites [4,5,6,7]. Some of these engineering works may lead to the violence of conventional ABX3 chemical formula. For example, single-layer 2D perovskites may adopt a general chemical formula of A2BX4 or ABX4 (depending on the charge of the A-site cations), while preserving the fundamental structural features of perovskites [8, 9]. Third, the A-site species contributes another dimension of flexibility to the perovskite structure. As cations occupy the cavity and balance the charge, metals are not the sole option for A-sites. Methlyammomium (MA) stands out as the pioneering and most well-known organic A-site species, forming hybrid organic-inorganic perovskites (HOIPs) [10, 11]. Beyond MA, an array of other organic cations with varying molecular sizes, functional groups, molecular lengths, and chirality can be introduced. These diverse possibilities introduce numerous degrees of freedom to perovskite materials, opening up extensive avenues for cutting-edge experimental and theoretical investigations.
As a category of important semiconductors typically having direct bandgaps, high carrier mobility, long diffusion length, and remarkable structural flexibility, metal-halide perovskites (MHPs), especially hybrid organic-inorganic ones, are at the forefront of scientific interest and can serve as an extraordinary platform for structural-property relationship studies. According to data from the National Renewable Energy Laboratory (NREL), the efficiency of perovskite-based solar cells has surged from approximately 13% in 2013 to 26.1% by mid-2024 [12]. This meteoric rise establishes MHPs as the most rapidly advancing group within the realm of emerging photovoltaic materials. Moreover, MHPs exhibit substantial potential in various other optoelectric applications. These applications encompass laser sources, light-emitting diodes (LEDs), photodetectors, and photocatalysts, all of which have been explored and reported upon extensively [7].
As a consequence, computational simulations play a critical role in elucidating the physics behind MHP experimental observations and further driving the rational design of MHP semiconductors guided by the structure-property relationships. Utilizing quantum chemistry simulations, theoretical researchers can make predictions regarding key properties such as bandgap values, the localization or delocalization of frontier bands, spin-orbit coupling (SOC) character, and ion migration property across various types of perovskite materials [13, 14]. While the methodology for predicting these properties is relatively mature for conventional 3D bulk perovskites, understanding more complex systems is still a cutting-edge topic with a lot of research interests. First, low-dimensional HOIPs and nano-scale perovskites constitute a distinguished category of perovskites from their conventional 3D bulk counterparts. For example, they have even more compositional and structural flexibility, possess larger bandgaps, and feature higher exciton binding energy. Their properties often exhibit anisotropics stemming from the underlying crystal lattice. We have reported a series of works to improve the protocol to efficiently simulate these systems, systematically analyze the theoretical results, and correctly explain the experimental observations. Second, mainstream theoretical simulations of hybrid perovskites heavily rely on the availability of experimental geometries. We attempted to give structure prediction for unknown systems with rational sampling of the possible structural conformations. Third, the emerging symmetry-breaking and spin-selective properties are critical experimental discoveries within 2D and nano-scale HOIPs, usually involving chiral organic components. We provided a comprehensive understanding based on the electronic structure calculations, encompassing both qualitative and quantitative aspects of this phenomenon. This achievement not only represents a significant advancement in the realm of structure-property relationships for perovskites but also can provide valuable guidance for future experimental synthesis and material design endeavors.
2 Computational approaches
2.1 Density functional theory
The behavior of electrons plays a central role in determining the properties of solid-state materials. Ideally, one would like to solve the Dirac equation that better accommodates the relativistic effects (will be discussed later) but key features of this problem can be initially understood by considering the non-relativistic Schrödinger equation. By assuming the distribution of the potential field is not a function of time (making the Schrödinger equation time-independent), and the behavior of electrons can respond to a change of nuclei positions in a negligible time scale (Born-Oppenheimer approximation, meaning the positions of electrons and nuclei can be treated separately), one can reach a simplified version of the Schrödinger equation with the following form:
where \(\hat{T}=-\frac{1}{2}\sum _{i=1}^{N} \nabla _{i}^{2}\) is the electron kinetic energy term, \(\hat{V}_{\text {nuclear-electron}}=-\sum _{i=1}^{N} \sum _{A=1}^{M} \frac{Z_A}{r_{i,A}}\) is the nuclear-electron interaction term, \(\hat{V}_{\text {electron-electron}} = \sum _{i=1}^{N} \sum _{j>i}^{N} \frac{1}{r_{i,j}}\) is the electron-electron interaction term, \(\Psi\) is the electron configuration, E is the eigenenergy, N is the number of electrons, M is the number of nuclear, and \(Z_A\) is the nuclear charge. Within this simplified Schrödinger equation, the nuclear-nuclear terms are omitted. However, the electron-electron interaction term includes the coordinates of different electron pairs and thus creates a massive amount of summation terms in practical usage.
Density functional theory (DFT) is a method designed to circumvent the calculation of this complicated electron-electron term. Under this scheme, the probability of finding electrons at a position \(\textbf{x}\) is given by a spatial dependent density function \(n(\textbf{x})\). Kohn and Sham formulated the Hohenberg-Kohn theorem [15] and defined a practical scheme to calculate the electron density [16]. In their method, the electron kinetic energy and nuclear-electron energy terms are consistent with Eq. 1, but the single-particle assumption is adopted to consider the electron-electron interaction. Specifically, they consider the behavior of a non-interacting fractious particle (electron) in the electron density (\(n(\textbf{x})\)) of a system and calculate the coulomb interaction it can perceive. By definition, it will deviate from the exact electron-electron interaction term defined in Eq. 1. So, an additional “exchange-correlation” term must be introduced to compensate for this difference. In this sense, the single-particle orbital functions can be defined using the eigenvalue problem in Eq. 2:
where \(v_{xc}\) is the exchange-correlation term, \(\psi _i\) is the \(i^{th}\) Kohn-Sham orbital, and \(\epsilon _i\) is the eigenenergy of the \(i^{th}\) Kohn-Sham orbital. Once having all the single-particle orbitals, one can construct the electron density of this system using Eq. 3:
where \(\text {f}_i\) is the electron occupation number of orbital i. So, by inputting a physically reasonable initial guess, one can iteratively use electron density to obtain orbitals through the eigenvalue problem defined in Eq. 2, and use these newly obtained orbitals to update the electron density. This strategy has a formal name of “self-consistent field” (S.C.F.) method. Once the convergence is reached, we can yield a set of ground-state molecular orbitals (MOs) and their corresponding eigenenergies. By default, these output MOs are orthogonal to each other, namelythe canonical orbitals (COs).
As shown in the previous context, the exchange-correlation term is artificial and only has a conceptual meaning in Eq. 2. So, an explicit depiction of this term is essential before the practical usage of DFT. To resolve this issue, several types of density functional approximations (DFAs), for example, the local spin density approximation (LSDA), the generalized gradient approximation (GGA), meta-GGA, and hybrid functionals were constructed, yielding different degrees of accuracy that are well studied in benchmarks for different systems and problems [17]. For example, LSDA is a basic DFA based on the homogeneous electron gas model, only considering the electron density. The targets of LSDA are solid systems, especially metals. Furthermore, GGA and meta-GGA take the gradient of electron density and the second derivative of the electron density into account, giving them a more flexible mathematical formula and better performance for molecular systems and semiconductors. Generally, all GGA and meta-GGA functionals are part of the category known as “semi-local” functionals. Moreover, hybrid functional can be constructed by introducing the higher level Hartree-Fock (HF) exact exchange term [18], which can treat the self-interaction error [19] better. In general, the LSDA functional is considered to be an over-simplified method although may benefit from some random error cancelation effect in some cases [20]; GGA-level functionals can produce sufficiently accurate results for the total energy related properties of ground states, but the predicted bandgap values are usually too small [20]; hybrid functionals with carefully parameterized mixing factor and screening factor can generate relatively accurate bandgap values and lattice constants for solid systems [21,22,23].
Beyond DFT, there exist higher-level methods (e.g., the GW method [24]) with better justification than the hybrid functionals for the prediction of the energy band structure in solids and molecules. However, the highly demanding computational cost and slow convergence process restrict their usage in the context of real-system calculations [25]. So, most of the hybrid perovskite simulations mentioned below use GGA-level functionals at least for the geometry prediction, and some of them will adopt the hybrid functionals for a more accurate prediction of energy levels.
2.2 Van der waals corrections
In LDA, semi-local functionals, and even the HF method, the tail part of their energy curves typically cannot accurately capture long-range dispersion interactions. This long-range interaction is crucial to account for the stability and local geometry of hybrid perovskites, mainly affecting the interaction at the inorganic-organic surface. To solve this problem, several methods such as non-local vdW density functionals [26], the atomic pairwise dispersion corrections [27], and the many-body dispersion corrections [28, 29] were introduced.
Specifically, the Tkatchenko-Scheffler pairwise dispersion scheme [27, 30] is widely used in our study on hybrid perovskites. This TS-vdW energy correction is calculated by enumerating all possible atom pairs in a system and summing up their energy terms (shown in Eq. 4).
In this expression, \(R_{AB}\) represents the distance between atom A and B, \(R_{A}^0\) and \(R_{B}^0\) are the free-atom radii of atom A and atom B, and \(C_{6,AB}\) can be obtain from the \(C_6\) coefficient (taken from the self-interaction corrected TDDFT results reported by Chu and Dalgarno [31]) and atomic polarizability of element A and element B [27]. The damping function \(f_\text {damp}\) eliminates the potential singularity when \(R_AB\) approaches zero. So, the inter-atom TS-vdW energy term is a function of the distances between each pair of atoms. As an energy term depending on the electron density, the above TS-vdW energy correction can go into the Kohn-Sham equations and be implemented self-consistently, [32, 33] but a non-self-consistent calculation is simpler and will not give major changes [27].
Additionally, we want to highlight a major update of the original TS-vdW reported by Fedorov et al. in 2018 [30]. A more fundamental way of determining the free-atom radii from atomic polarizability was proposed, instead of using the artificial partition of electron density (which was the case in the original TS-vdW). This new method fixed the atomic radii overestimation of alkali, lanthanide, and actinide elements. Based on our recent benchmark work, the updated TS-vdW achieves comparable accuracy to the nonlocal many-body dispersion method [28, 29, 34].
2.3 Relativity
Another physical component that Kohn-Sham DFT does not explicitly cover is the relativistic effects, which have long been known to have strong impacts on the band structures and properties, especially for materials containing heavy elements. The influence, including scalar relativistic effects and spin-orbit coupling, is believed to increase roughly proportional to \(Z^2\), where Z is the atomic number.
The exact treatment of relativistic effects can be traced back to the Dirac equation, in which the wave function contains four components (4C). The complexity of this treatment, compared to the nonrelativistic one-component Schrödinger equation, used to impede the development of relativistic electronic structure calculations. Considering the four components, the computation for diagonalizing the Hamiltonian matrix grows by \(4^3 = 64\) times, along with a significant increase in memory consumption. Therefore, in the past, the treatment of relativistic effects in condensed matter physics has mainly been simplified into two levels of approximation: (1) the scalar relativistic (SR) approximation and (2) adding spin-orbit coupling correction to the SR approximation-abbreviated as the SR+SOC scheme.
The SR scheme is typically based on the zero-order regular approximation (ZORA) [35], which expands a four-component Hamiltonian operator in a power series and then only preserves the zero-order term. This term does not contain the physical quantity of orbital energy and thus is quite easy to handle. ZORA is by concept a two-component formalism, but when ignoring the spin effects (i.e., setting the Pauli matrix in the equation as 1), one obtains the so-called scalar (i.e., one-component) ZORA formalism which is quite easy to implement in first-principles codes [36]. The computational complexity of this approach is comparable to a non-relativistic regime. Specifically, it can be implemented even by directly modifying the kinetic energy operator in the non-relativistic Schrödinger equation. However, the neglect of spin makes it incapable of handling systems with significant SOC effects. Moreover, since ZORA neglects other higher-order expansion terms of the Hamiltonian that contain orbital energy, this approach always leads to divergent results for inner shell electrons, and therefore should typically be combined with pseudopotentials or other methods like augmented plane waves [37].
The SR+SOC recipe, as a widely used strategy in condensed matter physics, introduces an SOC correction to the aforementioned SR scheme (Eqs. 5 and 6), enabling the treatment of spin-orbit interaction. This approach can be conceptually classified as a two-component algorithm regarding computational complexity. SOC correction is typically added via perturbation theory [38], either self-consistently or in the last step of the S.C.F. calculation. The latter one sacrifices some precision but can significantly save computational effort [36]. It can be understood that the basis functions employed in the SR+SOC scheme are still scalar functions within the SR framework, which are incapable of describing relativistic spinors [39]. Therefore, for specific systems or properties, one may need to add local orbitals to fix the incomplete basis set [40].
Here, we would like to specifically highlight a quasi-four-component (Q4C) formalism we have recently developed [41]. Fundamentally, the four-component Dirac equation deals with both electrons and positrons, whose energy level difference is about one million eV. However, the electronic structure problems of interest in condensed matter physics (bonding process, electron transfer, etc.) are typically limited to the level of tens of eV, which is negligible compared to the magnitude of one million. That means the energy change in electronic structures during the bonding process hardly causes any change in the positronic structures. So, positronic effects in these studies are somewhat redundant, as they significantly increase computational demands without improving accuracy. Based on this background, the essence of Q4C is to freeze the contribution of positrons and merely treat electrons, thus reducing the computational effort by two components while handling all relativistic effects at the four-component level. This method has been proven to offer computational efficiency comparable to two-component algorithms while achieving accuracy equivalent to traditional four-component methods. Combined with localized numerical atomic basis sets in FHI-aims, Q4C can now compute perovskite systems with hundreds of atoms in a unit cell in a fully relativistic manner [41]. This is expected to facilitate the investigation of perovskites, in which heavy atoms (e.g., Pb and Bi) and spin-polarized atoms (e.g., Cu) commonly exist.
Considering that the primary objective of the studies reviewed here is to reveal the qualitative physical results, we will in the following context mainly present the results in a non-self-consistent SR+SOC manner, as also available in the FHI-aims code package [42].
3 Simulation and property prediction
3.1 Unit cell choosing and band folding
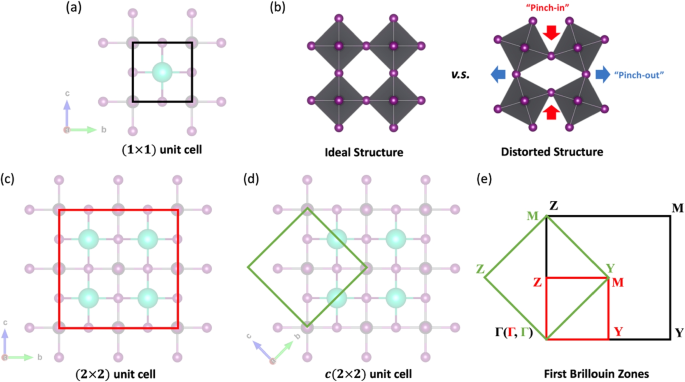
In an ideal perovskite structure, all [BX6] units are regular octahedrons with B atom located at the geometric center, and all the inter-octahedron connections (B-X-B bond angles) are 180\(^{\circ }\). In 2D perovskites, the primitive unit cell contains only one set of [BX6] octahedron and the A cation and is named as (1\(\times\)1) unit cell (shown in Fig. 2a). Several previous works attempted to theoretically understand the perovskite systems with this type of unit cell [43, 44].
However, structural flexibility is one critical feature of perovskites, mainly due to the bonding nature of corner-sharing octahedrons. This feature is reflected by the tilting of octahedrons, leading to the “pinched-in” and “pinched-out” inter-octahedron connections shown in Fig. 2b. This type of distortion has been illustrated by various experimental and theoretical investigations. Consequently, the primitive (1\(\times\)1) unit cells are no longer suitable to host this distortion pattern, and the expanded (2\(\times\)2) and c(2\(\times\)2) unit cells are constructed (shown in Fig. 2c and d). Taking the simplest 2D perovskite model (without any distortions or octahedron rotations) as an example, the (2\(\times\)2) unit cell features an intuitive elongation of (1\(\times\)1) unit cell edges by two times, resulting in a 4-times expansion of the unit cell size, in contrast, the c(2\(\times\)2) unit cell only causes a 2-times expansion, but a 45°-rotation is applied.
Structural distortion and different unit cell choosing for 2D perovskites. a The primitive (1\(\times\)1) unit cell. b The “pinched-in” and “pinched-out” inter-octahedron distortion in perovskites. c The (2\(\times\)2) unit cell. d The c(2\(\times\)2) unit cell. e A conceptual comparison of the BZs corresponding to the (1\(\times\)1), (2\(\times\)2), and c(2\(\times\)2) unit cells
As a result, the Brillouin zones (BZs) corresponding to these three different unit cells (Fig. 2b, c, and d) are correlated by folding and rotating operations. When the real-space unit cell expands (e.g., by two times), its first BZ in the reciprocal space shrinks (e.g., by half). This shrinking does not mean the loss of electron state information along this path. Instead, it leads to a more compact expression in the smaller BZ based on the new periodic boundary. The way of compressing the electron states information into the new BZ is just like folding a piece of paper, making this whole process called “band folding” [45]. Figure 2e conceptually shows the BZs of the (1\(\times\)1), (2\(\times\)2) and c(2\(\times\)2) 2D perovskite unit cells. More details about the band folding in 2D perovskite and how k-paths in different BZs correlate to each other can be found in Ref. [46].
3.2 Structure prediction
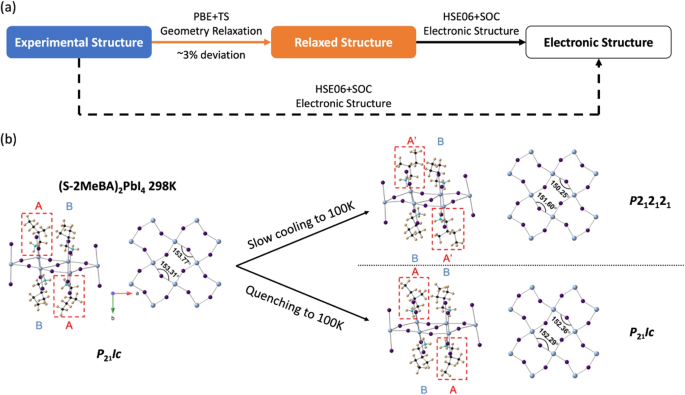
The atomic structure serves as the foundation for the electronic-structure-based theoretical investigation of perovskites. In the case of well-crystallized systems, high-resolution experimental structures for 2D hybrid perovskites can be obtained through X-ray diffraction (XRD). Starting from the experimental structure, we typically employed a DFT-based structural relaxation/optimization as a pre-processing to eliminate apparently wrong or unphysical interactions (e.g., caused by missing atoms or atoms too close to each other). Our past research indicated that subsequent DFT structure relaxation employing proper exchange-correlation functional (e.g., the semi-local Perdew-Burke-Ernzerhof (PBE) functional [47]) along with long-range interaction (e.g., the TS vdW correction [27]) is relatively efficient and accurate, only introducing approximately 3\(\%\) structural deviation from the XRD experimental structures [48,49,50]. So, XRD-based experimental structure and simulation-based relaxed structure usually coexist in many of our previous publications and in the database [51, 52]. This simulation approach involving geometry relaxation is demonstrated in Fig. 3a.
Starting from this point, we also tried to directly step into the high-precision single-point DFT electronic structure calculation with highly-confident, high-resolution XRD experimental structures. This strategy of skipping the geometry relaxation can significantly simplify the problem, especially for intricate systems. For instance, (S)-(-)-2-methylbutylammonium lead iodide ((S-2MeBA)2PbI4) is a 2D hybrid perovskite with temperature-sensitive atomic structures [53]. Upon gradual cooling from ambient conditions (298K) to cryogenic temperatures (100K), this compound undergoes a phase transition at \(\sim\)180K, whereas rapid cooling (quenching) predominantly retains its room-temperature structure (illustrated in Fig. 3b). The 100K-slow-cooled configuration exhibits different organic cation conformations and slightly increased octahedral distortions compared to the 100K-quenched structure, resulting in a higher-level symmetry breaking. These geometry differences can easily diminish in the DFT-based geometry relaxation. So, in this study, we chose to directly utilize the XRD geometries for high-accuracy electronic structure computations, bypassing any potential biases introduced by the PBE+TS method. Our approach effectively captured meV-level differences in the electronic structures, affirming the modulation of spin properties in 2D hybrid perovskites via a kinetic way. In another example directly involving XRD atomic structures, we modeled a series of metal-halide perovskite systems containing Ag, Fe, and Mn using the hybrid functional, and qualitatively predicted the trend of bandgap change in this series [54]. In general, our experience shows that the simulation strategy including DFT-based geometry relaxation is relatively safe for most hybrid perovskite systems, while directly using high-resolution experimental structures (when available) can be a relatively reliable and wise way around for complex problems (e.g., systems with highly-sensitive atomic structures or complex interactions).
a Two ways to conduct DFT simulation for hybrid perovskites with experimental structures. The conventional approach involves two stages. The first stage is geometry relaxation based on the PBE functional with TS vdW correction, which is efficient and accurate in terms of geometry prediction. The second stage is single-point electronic structure calculation based on the hybrid functional and spin-orbit coupling, which is significantly more costly but can provide more accurate electronic structures. For some intricate systems, high-resolution experimental structures could also be directly used for single-point electronic structure calculations. b An example that experimental XRD structures were directly utilized in the electronic structure calculations. The critical structural differences between (S-MeBA)2PbI4 system that was slowly-cooled from 298K to 100K and quenched from 298K to 100K are minimal and can diminish in PBE+TS geometry relaxation. So, directly using experimental XRD structures is the only way to capture the electronic structure difference between these two structures (reproduced from Ref. [53])
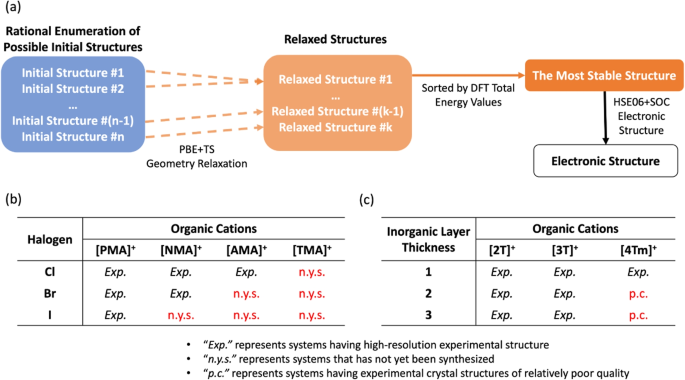
Apart from relaxing the experimental structures, DFT simulations can also facilitate the determination of atomic structure in a reverse manner. DFT total energy of the relaxed structures directly correlates with the stability of different conformations of a compound. Starting from a set of rationally constructed initial geometries, the DFT-based structure optimization algorithm can either generate different relaxed geometry conformations with different total energy values or reach the same energy basin, providing the same relaxed geometry (shown in Fig. 4a). For example, in our investigation focusing on a series of oligoacene-based 2D lead-halide perovskites (Fig. 4b), we extracted featured geometry patterns (e.g., symmetry elements and organic cation conformations) of the known systems and enumerated all possible combinations of these features to construct multiple initial geometries for each compound [55]. After DFT relaxations starting from these initial geometries, our strategy achieved a satisfying successful rate (5/6) and high accuracy (<3\(\%\) structure deviation) in retrieving the experimental geometries when tested on a total of six experimentally known systems (phenylmethylammonium lead chloride ((PMA)2PbCl4), phenylmethylammonium lead bromide ((PMA)2PbBr4), phenylmethylammonium lead iodide ((PMA)2PbI4), naphthylmethylammonium lead chloride ((NMA)2PbCl4), naphthylmethylammonium lead bromide ((NMA)2PbBr4), and anthrylmethylammonium lead chloride ((AMA)2PbCl4)). Furthermore, we utilized this strategy on six “not-yet-synthesized” compounds (naphthylmethylammonium lead iodide ((NMA)2PbI4, anthrylmethylammonium lead bromide ((AMA)2PbBr4), anthrylmethylammonium lead iodide ((AMA)2PbI4), tetrylmethylammonium lead chloride ((TMA)2PbCl4), tetrylmethylammonium lead bromide ((TMA)2PbBr4), and tetrylmethylammonium lead iodide ((TMA))2PbI)4)) within this oligoacene-based 2D hybrid perovskite series and obtained a set of reasonably predicted stable geometries and their corresponding electronic structures. Another similar example is our study on a series of nine oligothiophene-based 2D lead-iodide perovskites with tunable inorganic layer thickness (Fig. 4c) [56]. Within these compounds, long tails of the organic cations and multilayer inorganic domain together lead to relatively hard XRD measurements. So, we rationally constructed the initial geometries for (3T)2(MA)2Pb3I10 (a 2D perovskite containing conjugated tri-thiophene groups in the organic domain and three consecutive Pb-I inorganic layers in the inorganic domain) and (4Tm)2(MA)2Pb3I10 (a 2D perovskite containing conjugated quarter-thiophene groups in the organic domain and three consecutive Pb-I inorganic layers in the inorganic domain) based on systems with known experimental geometries. Furthermore, DFT-based relaxation reproduced the lattice vectors suggested by the XRD measurements, and the electronic structure calculations based on the relaxed structures successfully validated the experimental observations of active photoluminescence or quenched photoluminescence within the compounds studied.
a A schematic illustration of how DFT helps to predict the atomic structure of a system (and its corresponding electronic structure) when high-resolution experimental structure is not available. Starting from a set of rationally constructed initial geometries, PBE+TS geometry relaxation may bring different initial structures into the same energy basin or generate different relaxed structures from different starting points. The stability of the relaxed structures can be determined based on their DFT total energy values. Then, this suggested atomic structure can be used in the electronic structure calculation with higher-level methods (e.g., the HSE06+SOC method). b A table showing the twelve oligoacene-based 2D HOPs studied in our previous work. Half of them have high-resolution experimental structures and half of them are not yet been synthesized (reproduced from Ref. [55]). c A table showing the nine oligothiophene-based 2D HOIPs studied in our previous work. Seven of them have high-resolution experimental crystal structures and the experimental structures of the rest two are of relatively poor quality (reproduced from Ref. [56])
3.3 Frontier band alignment
The electronic band structure is a clean way to describe electron energy levels in solid-state materials. Because of the widely existing periodicity in solids, an electronic band structure is an “energy versus k-path” plot. Specifically, the k-paths refer to some featured vectors in the BZ, and the energy refers to the discrete DFT converged electronic state eigenenergies at a specific k-point. Depending on the electron occupancy of each state, the energy bands near the Fermi level are categorized into valence bands (VBs) if occupied and conduction bands (CBs) if unoccupied. The highest occupied state is called valence band maximum (VBM) and the lowest unoccupied state is called conduction band minimum (CBM) (shown in Fig. 5a). Typically, VBM and CBM are directly related to electrical and optical properties, such as conductivity, photo-absorption, and photoluminescence, and thus are crucially important.
Classic HOIPs (e.g., Pb- and Sn-based HOIPs) show superior semiconducting properties with bandgaps ranging from approximately 1 eV to 3 eV, depending on their compositions and structures [1, 57, 58]. In 3D HOIPs, the size and structural complexity of the organic cations are constrained by the available space for A-site species. Consequently, the inorganic components always have higher VBM and lower CBM compared to organic cations. In contrast, the 2D HOIP inorganic framework can accommodate larger organic cations with diverse functional groups and structural flexibility [8, 9]. Together with the increased inorganic bandgap, organic species become potential participants in the frontier bands. Consequently, for theoretical investigations on these systems, a detailed depiction of the origin (e.g., the specific element or atom contribution to each band) of each frontier electronic band becomes critically important.
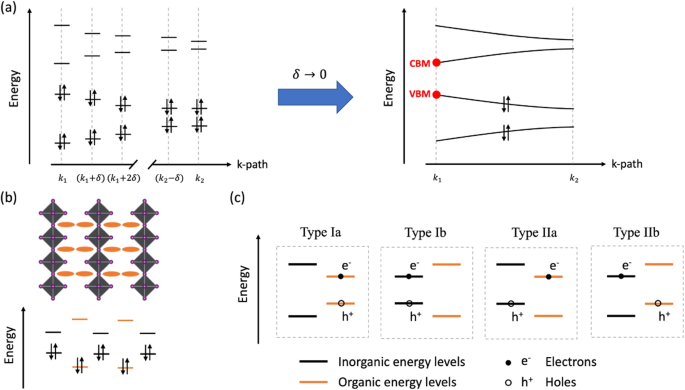
a A conceptual illustration of band structure. Each k-point in reciprocal space has its own set of discrete electronic states with different eigenenergy values. In DFT band structure calculations, we sample dense grids along each selected k-path and obtain “energy versus k-path” curves (band structure). VBM and CBM points are highlighted in red. b A conceptual illustration of how inorganic (black lines) and organic (orange lines) frontier bands correspond to the 2D inorganic (black octahedron layers) and organic moieties (orange oval layers) in real space. c Four possible quantum well types in 2D HOIPs. The carriers (electrons and holes generated by the excitation process) may be preferentially localized in different geometric moieties (inorganic or organic moieties) depending on the relative position of inorganic and organic frontier energy levels
Technically, the converged DFT COs are represented by a linear combination of the input basis functions, with numerical arrays (eigenvectors) recording the combination coefficients. In this regard, these eigenvectors contain information to depict the composition of a state. While each basis function is associated with a specific atom, the basis functions are not orthogonal to each other due to their overlap in real space. Therefore, instead, we considered the atomic contribution as “charge contribution”, and utilized the Mulliken population analysis [59] to handle the contribution decomposition. Mulliken population analysis depends on the electron density and overlap matrix. As shown in Eq. 3, the electron density of the whole system is defined to include all converged electronic states (\(\psi _i(\textbf{x})\)) with non-zero occupation numbers \(\text {f}_i\). The density can be further decomposed into basis function pairs (\(\phi _\nu\), \(\phi _\mu\)) together with their density matrices (\(P_{\nu \mu }=\sum _{i} \text {f}_i c_{\nu , i} c_{\mu , i}^*\), where \(c_{\nu , i}\) and \(c_{\mu , i}\) are linear combination coefficients of basis function \(\nu\) and \(\mu\) when forming the \(i^{th}\) eigenstate):
For a given set of (\(\nu , \mu\)), the corresponding term can be extracted and integrated over the whole space to form the overlap population (charge):
where the \(\int [\phi _\mu ^* \phi _\nu ] d\textbf{x}\) and \(\int [\phi _\nu ^* \phi _\mu ] d\textbf{x}\) terms are elements \(S_{\mu \nu }\) and \(S_{\nu \mu }\) in the overlap matrix S. Then, a charge contribution due to basis functions \(\phi _\nu\) and \(\phi _\mu\) can be assigned by distributing the overlap charge quantity \(Q(\nu , \mu )\) equally to each side. After removing the summation over all states (\(\sum _{i}\)) in the P term and sum over all the basis functions for \(\phi _\mu\), we can define a charge contribution from any specific basis function \(\phi _\nu\) to any specific electronic state i. After adding the information of which atom the basis functions come from, we can further add another layer of summation for basis functions belonging to each specific atom (\(\sum _{\text {all}\ \nu \ \text {from atom} A}\)) and assign the contribution to that atom (\(M_{A,i}\)):
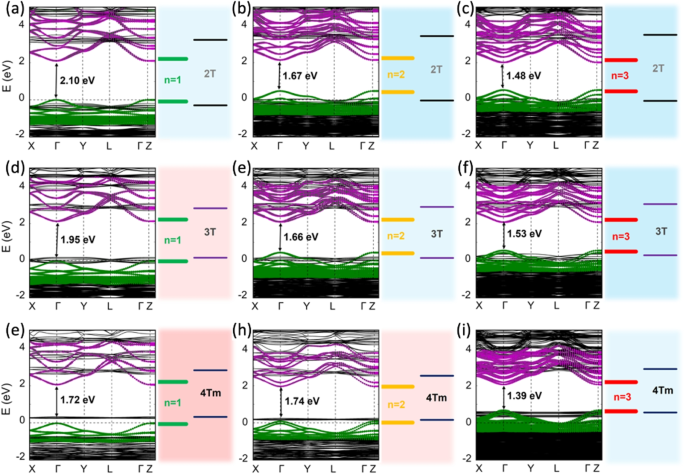
A series of notable research has demonstrated that the frontier bands of 2D HOIP systems can be artificially tuned through meticulous engineering of their inorganic and organic components. Due to the charge carrier confinement caused by the spatially separated inorganic and organic layers, 2D HOIPs can form atom-level quantum well structures (shown in Fig. 5b and c). Gao et al. demonstrated that incorporating organic cations with varying conjugation lengths can result in different types of quantum wells [49]. Park et al. further developed this approach by engineering the thickness of the inorganic 2D layers, enabling more systematic fine-tuning of the quantum well types [56]. In these investigations, we helped to understand the quantum well types from a theoretical perspective. The hybrid functional Heyd-Scuseria-Ernzerhof (HSE06) [21, 22] was employed to achieve converged DFT electronic structures and then the Mulliken population analysis was applied. Through this process, we obtained quantitative values of atomic contribution to the frontier bands and correctly predicted the quantum well types in these 2D HOIPs that lead to active photoluminescence or photoluminescence quenching in the experimental observations. Examples of the results of Mulliken population analysis and frontier level alignment are shown in Fig. 6.
The HSE06+SOC band structures and frontier level alignment results of (a) (2T)2PbI4 (2T, n= 1), (b) (2T)2(MA)Pb2I7 (2T, n= 2), (c) (2T)2(MA)2Pb3I10 (2T, n= 3), (d) (3T)2PbI4 (3T, n= 1), (e) (3T)2(MA)Pb2I7 (3T, n= 2), (f) (3T)2(MA)2Pb3I10 (3T, n= 3), (g) (4Tm)2PbI4 (4Tm, n= 1), (h) (4Tm)2(MA)Pb2I7 (4Tm, n= 2), (i) (4Tm)2(MA)2Pb3I10 (4Tm, n= 3). These nine systems correspond to the systems listed in Fig. 4c, which are studied in Ref. [56]. The size of the green and purple dots in the band structures represents the atomic contribution obtained through Mulliken population analysis, showing the inorganic contributions on each band. Frontier level alignments showed that the (2T)2PbI4, (2T)2(MA)Pb2I7, (2T)2(MA)2Pb3I10, (3T)2(MA)Pb2I7 and (3T)2(MA)2Pb3I10 systems have “Type Ib” quantum well, leading to active photoluminescence observations in experiments. In contrast, the remaining four systems have “Type IIb” or “Quasi Type IIb” quantum well, leading to photoluminescence quenching in experiments. (reproduced from Ref. [56])
3.4 Chirality and spin splitting in frontier bands
Breaking of inversion symmetry is important for multiple physical properties in inorganic systems. Especially in conjunction with relativistic effects such as SOC, it engenders rich condensed matter phenomena, such as the quantum spin Hall effect [60] and Rashba-Dresselhaus (R-D) coupling [61,62,63] in non-magnetic systems, and exotic spin topologies including chiral domain walls [64]. These properties can help materials gain promising applications in electronic, magnetic, and spintronics technologies [65, 66]. Specifically, in band structures, a lack of inversion symmetry (in the real space structure) typically means the splitting of spin-reverse states (shown in Fig. 7a, in contrast to the degenerated spin-up and spin-down states shown in Fig. 5a.
Chirality, a fundamental property in organic chemistry, is accompanied by the absence of an inversion center and mirror plane in a molecule. Organic chemists can create a chiral center through relatively straightforward synthetic engineering by attaching four different functional groups to an \(sp^3\) hybridized carbon atom. 2D HOIPs, thanks to their high compositional and structural flexibility, can serve as an extraordinary platform for the incorporation of complex organic cations. Recently, experimental chemists reported a series of successful syntheses of HOIPs including chiral organic cations, showing polarized photon absorption and/or emission properties [50, 53, 67,68,69,70]. These achievements provide theoretical chemists with a good opportunity to study the electron spin property and the mechanism of chirality transfer within 2D hybrid perovskite systems.
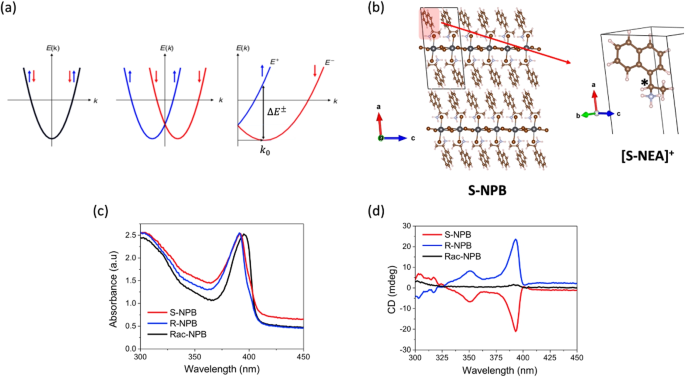
a Schematic representations of a two-fold spin-degenerate electronic band and spin-polarized sub-bands (red and blue) separated in k-space due to the SOC and inversion asymmetry along one dimension. \(\Delta E^\pm\) denotes the energy difference between the two band branches at the characteristic momentum (\(k_0\)). b In the S-NPB system, the organic moiety is composed of S-NEA organic cations. The \(sp^3\) \(\alpha\)-C of the S-NEA cation is a chiral center connecting four different function groups. c UV-Vis linear absorption spectra and (d) CD spectra recorded at room-temperature for thin films of racemic-, R- and S-NPB. (reproduced from Ref. [67])
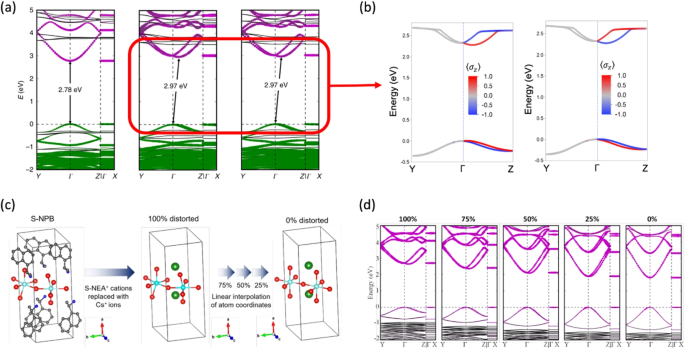
One featured example is the systematic study of Pb-Br-based 2D HOIPs containing R-1-(1-naphthyl)ethylammonium (R-NEA), S-1-(1-naphthyl)ethylammonium (S-NEA), and a racemic mixture of R-NEA and S-NEA (racemic-NEA) cations (shown in Fig. 7b) [67]. Specifically, the synthesized (R-NEA)2PbBr4 (R-NPB) and (S-NEA)PbBr2PbBrPbBr4 (S-NPB) show similar photon absorption peaks at 390 nm but completely reverse circular dichroism (CD) signals. In contrast, (racemic-NEA)PbBr2PbBrPbBr4 (racemic-NPB) has the photon absorption peak but negligible CD signal (shown in Fig. 7c and d). Active CD signal is a direct outcome of the chiral point group, and the signal sign difference between R- and S-NPB indicated their opposite absolute configurations. In the DFT band structures considering the SOC effect, we observed significant spin splitting in the conduction bands of R-NPB and S-NPB (Fig. 8a). Mulliken analysis showed the inorganic original (Pb species) of this splitting. We then applied the Pauli matrices (\(\vec {\boldsymbol{\sigma }} = (\sigma _x, \sigma _y, \sigma _z)\)) to each electron state to obtain the 3D spin vector of each state under the quantum Heisenberg model [71] (Eq. 10).
a The HSE06+SOC electronic band structures of racemic-NPB, S-NPB, and R-NPB. The contributions from Pb atoms and Br atoms are shown in purple and green dots. The R-D spin splitting in chiral NPB systems leads to indirect bandgaps. b The PBE+SOC frontier bands and spin textures (along the stacking direction) of chiral NPB systems. c A model study of the origin of spin splitting in chiral NPB systems: the chiral organic cations were replaced by Cs cations and the inorganic geometry distortions were gradually reduced. d The HSE06+SOC electronic band structures of the simplified model systems. The R-D spin splitting gradually disappeared upon going from the 100\(\%\) distorted structure to the 0\(\%\) distorted structure. (reproduced from Ref. [67])
In Fig. 8b, we present the spin-polarized inorganic sub-bands of R- and S-NPB showing opposite spin textures along the stacking direction of the system, validating the control of R-D spin polarization using the chiral organic cations. Moreover, we further replaced the chiral organic cations in the S-NPB system with Cs+ cations and created a series of model structures with different degrees of inorganic distortions by interpolating the atomic positions in S-NPB and the “ideal” 2D perovskite structure (without any distortion). Band structures of these model systems showed that R-D spin splitting is not coupled with the existence of chiral organic cations but is closely related to the magnitude of asymmetric inorganic distortion (Fig. 8c and d).
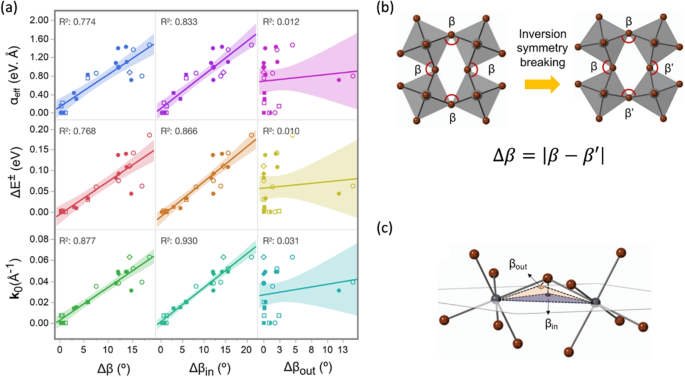
After confirming the inorganic origin of R-D spin splitting in chiral 2D HOIPs, our subsequent goal under this topic was to identify the key geometric feature(s) determining R-D splitting. In Ref. [68], a total of twenty-two different 2D HOIPs including chiral or achiral organic cations were considered. To quantify the structural features, we categorized the distortions into “intra-octahedron” and “inter-octahedron” distortions. Under the “intra-octahedron” category, we set up two geometric descriptors featuring the bond length and bond angle variations within each octahedron. Under the “inter-octahedron” category, we set up five geometric descriptors featuring the degrees of distortion (maximum deviation from the ideal 180\(^\circ\) connection) and the asymmetric distortion (different inter-octahedron distortions angles) between octahedron pairs. To quantify the magnitude of spin splitting in DFT-based frontier bands, we measured the R-D splitting value (\(\Delta E^\pm\), the energy difference between the spin reverse sub-bands), the R-D splitting position (\(k_0\), the off-centering of CBM from the \(\Gamma\) point), and the effective R-D coefficient (\(\alpha _{\text {eff}} = \frac{\Delta E^\pm }{2k_0}\)). In a linear regression analysis, all three quantities (\(\Delta E^\pm\), \(k_0\), \(\alpha _{\text {eff}}\)) featuring the spin-splitting magnitude correlate strongly with the inter-octahedron distortion angle disparity \(\Delta \beta\) (with \(R^2 > 0.7\)). To be more specific, this angle disparity within the inorganic 2D plane (\(\Delta \beta _{\text {in}}\)) serves as the critical component (with \(R^2 > 0.8\)), whereas the out-of-plane component (\(\Delta \beta _{\text {out}}\)) barely has an influence (with \(R^2 \approx 0.01\)). All the other structural descriptors are much less related to the spin splitting with \(R^2 < 0.5\). Linear regression analysis and the definition of \(\Delta \beta\), \(\Delta \beta _{\text {in}}\), and \(\Delta \beta _{\text {in}}\) are shown in Fig. 9. More details can be found in Ref. [46, 68]. A later work reported by Maurer et al. [72] focused on the intra-octahedron distortions and reached a similar conclusion, although the geometric features were expressed differently. Our later model study further showed that the geometric inversion symmetry breaking directly causes the spin splitting instead of being mediated by the dipole field. This direct structure-property correlation enables a unique and fast route to an informed discovery/screening of promising spin-selective 2D HOIPs, purely based on crystal structure information.
a Linear regression analysis showed that the inter-octahedron distortion angle disparity (\(\Delta \beta\)) correlates strongly with the magnitude of R-D spin splitting in 2D HOIPs (with \(R^2>0.8\)). Specifically, this angle disparity within the inorganic 2D plane (\(\Delta \beta _{\text {in}}\)) is the key component (with \(R^2 > 0.8\)). The shaded regions in the plots represents the 95\(\%\) confidence intervals. b Definition of the inter-octahedron distortion angle disparity (\(\Delta \beta\)) that breaks the inversion symmetry of the system. c An illustration of how inter-octahedron distortion angle is projected to the “in-plane” direction and “out-of-plane” directions of the 2D plane. (reproduced from Ref. [68])
4 Summary
This article mainly accounts for our recent progress on the DFT-based investigations of complex 2D HOIP systems. First, we showcased a relatively mature protocol of the DFT simulation on this type of system, which can provide a good balance between accuracy and computational cost. Besides the conventional simulation tasks with high-quality crystal structures, our protocol shows the potential capability to explore experimentally unknown systems. Second, we demonstrated that 2D HOIP systems can be a good host for atomic-scale quantum wells, using the converged DFT electronic structure result and the Mulliken population analysis as a post-processing algorithm. This method is a powerful tool to give a quantitative depiction of the electronic state composition and can be applied to other systems. Finally, we presented our in-depth study of the chirality and spin-splitting effects within 2D HOIPs. Apart from predicting the frontier-band spin splittings based on a given atomic structure, we successfully identified the specific structural descriptor dominating the symmetry breaking and spin splitting in known 2D HOIP systems. This conclusion was also validated on the 2D surface of nano-scale HOIP systems.