1 Introduction

Due to applications of television broadcasting, mobile phones, global positioning systems (GPS), Bluetooth, WLANs, etc., our space is filled with signals in different frequency bands. Bandpass filters are required to avoid interference between these different applications [1, 2]. The filters are also widely used in many advanced optical and quantum technologies [3,4,5,6,7,8]. For the fifth-generation (5G) telecommunication standard [9, 10], bandpass filters with high-frequency and wide bandwidth are essential [2, 11]. Different types of bandpass filters have been employed, such as electromagnetic-wave based low temperature co-fired ceramic (LTCC) [12, 13], integrated passive device (IPD) [14, 15], and metasurfaces [16], and acoustic-wave based surface acoustic wave (SAW) [17], and bulk acoustic wave (BAW) filters [18, 19]. A combination of the IPD and the acoustic technology has also been reported [20]. Because sound velocity in a typical solid material is a factor of five orders lower than that of the electromagnetic wave, the acoustic-wave-based SAW or BAW resonators can be built in small sizes. These acoustic resonators have dominated the filter market up to date [21]. Besides applications in the filters, the SAW and BAW devices also have widespread applications in sensors [22, 23], actuators [24], quantum acoustics [25], and others [26].

Although their structures are different, both the SAW and BAW resonators are fabricated based on piezoelectric materials which are a class of materials that can transduce mechanical strain to electrical signal and vice versa. The piezoelectric behavior was discovered by Pierre Curie and Jacques Curie as early as 1880 [27], and its origin is that the crystalline material lacks an inversion symmetry [28]. Quartz is the first reported piezoelectric structure, and it is widely used in quartz crystal microbalance (QCM) [29]. Up to date, a large number of piezoelectric materials have been reported, such as aluminum nitride (AlN) [30,31,32], zinc oxide (ZnO) [33], lead zirconate titanate (PZT) [34] and lithium niobate (LiNbO3) [35, 36]. Among these materials, AlN shows promising stability at elevated temperatures, good thermal conductivity, strong mechanical strength, low-temperature coefficient of frequency (TCF), and compatibility with the complementary metal-oxide-semiconductor (CMOS) technology [37, 38]. These advantages make the AlN an ideal piezoelectric material for the SAW and BAW resonators.

In this paper, research progress in the AlN-based SAW and BAW resonators for bandpass filters is briefly reviewed. Typical structures of the SAW and BAW resonators are introduced first. Significant performance parameters of the resonators and common filter topologies are discussed. Regarding the resonator structure, the pristine AlN and its alloys for the piezoelectric layer are highlighted, and existing electrodes and substrates are also elaborated. Finally, a summary is provided and several possible research directions are suggested.

2 Structures of the SAW and BAW resonators

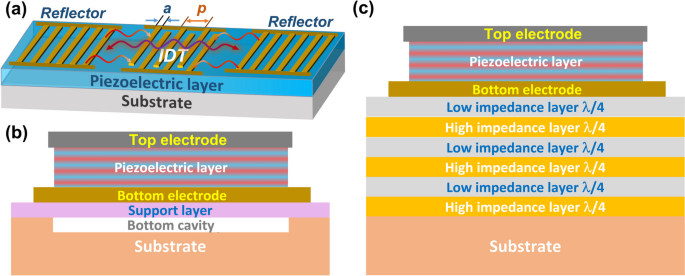
The typical structures of SAW [17] and BAW [1] resonators are presented in Fig. 1. Regarding the SAW structure in Fig. 1a, the surface of piezoelectric material is deposited by interdigital transducers (IDTs) [39]. Acoustic reflectors are also employed for confining mechanical energy [40]. Based on the inverse piezoelectric property, surface-acoustic modes can be generated by connecting neighboring fingers of IDT to an alternating electrical signal. The electromagnetic wave could also be detected by the IDT through the piezoelectric effect. The Rayleigh wave is one commonly used surface-acoustic mode [41, 42], which is a coupled wave of longitudinal and transverse modes. Other surface acoustic waves are also reported, such as the Lamb, Love, and Gulyaev-Bleustein [42, 43]. The resonance frequency is mainly determined by the spatial periodicity p and the acoustic velocity ν:

\({f}_{r}=\frac{v}{p}\)
(1)

where ν is dominated by the piezoelectric material, but it is also influenced by the IDT weight. To reduce insertion loss, various schemes have been proposed to suppress spurious modes, such as using weighting transducers [44]. Because the resonance frequency depends on the p value, it is difficult to operate the SAW resonator above 2 GHz due to limitations in lithography and pattern technology [45]. The SAW also suffers from limited power-handling capability at high frequencies [21].

Fig. 1
figure 1

Schematic diagrams of a the SAW resonator, b the thin-film BAW resonator (TFBAR): airbag-type, and c the solidly mounted BAW resonator (BAW-SMR)


Different from the SAW, the BAW is based on the thickness extensional mode (longitudinal acoustic wave) which is generated by connecting the alternating electrical signal on the top and bottom sides of piezoelectric material. The thickness t of the piezoelectric layer is typically designed as half of the wavelength (λ/2), thus the resonance frequency fr is equivalent to:

\({f}_{r}=\frac{{v}_{l}}{2t}\)
(2)

where νl is the velocity of the longitudinal wave. Since the frequency is inversely proportional to the t, the BAW with a thin piezoelectric layer has attracted extensive attention for high-frequency filters. Figure 1b and c present two typical BAW structures: a thin film BAW resonator (TFBAR) [46] and a solidly mounted BAW resonator (BAW-SMR) [47], respectively. The working principles of these two resonators are similar, but they use different approaches to confine the mechanical energy. The TFBAR uses an air cavity to confine the energy, but the BAW-SMR employs a Bragg reflector. The reflector is constructed by alternating layers with significantly different acoustic impedances [48], such as Mo with SiO2 [47], and W with SiO2 [49]. The thickness of each layer in the reflector equals λ/4. Similar to the IDT design in the SAW, modifications in BAW electrodes have also been performed to eliminate spurious modes, such as using an asymmetrically shaped top electrode [50, 51], and constructing a frame at the edge of the top electrode [52]. The TFBAR generally has a lower insertion loss compared to the SMR-type, but the latter might be superior for high-frequency applications because it possesses better thermal conductivity and smaller layer stress [21].

3 Key performance parameters

After introducing their structures, the key performance parameters of the SAW and BAW resonators for filters are discussed. Due to the piezoelectric and inverse piezoelectric effects, the mechanical and electrical energy can be converted in the piezoelectric material. The electromechanical coupling constant is defined as a measure of the efficiency of energy conversion. For the longitudinal wave along the z-axis, the electromechanical coupling constant \({k}_{33}^{2}\) of the piezoelectric material is calculated as [53]:

\({k}_{33}^{2}=\frac{{d}_{33}^{2}}{{\varepsilon }_{33}{s}_{33}}\)
(3)

where d33, ε33 and s33 denote the piezoelectric strain constant, the permittivity parameter, and the elastic compliance constant along the z-axis, respectively. The electromechanical coupling constant for more vibration modes can be found in Ref. [28], and it is denoted as kt2 for a general mode. Each SAW and BAW resonator has two resonance frequencies fs and fp considering the couplings of different phase waves, where the series resonance fs and the parallel resonance (or anti-resonance) fp correspond to the maximum admittance and the maximum impedance of the resonator, respectively [54]. The relationship between the kt2, and fs and fp can be simplified as follows [28]:

\({k}_{t}^{2}=\frac{{\pi }^{2}}{4}\frac{\Delta f}{{f}_{p}}\)
(4)

where Δf denotes Δf = fp-fs. The detailed derivation process for this equation was presented in Refs. [28, 55]. The kt2 is an important parameter which determines the resonator bandwidth. Its value is mainly determined by the piezoelectric material, but the electrode and resonator structure could decrease it [28, 54].

Besides the kt2, quality factor Q is another significant performance parameter of the resonator, which implicates the filter selectivity. A high Q implies low insertion loss and good isolation and rejection [11]. The Q is also the ratio between the energy stored to the energy lost in the resonator [2, 56]. Different approaches have been adopted for evaluating the Q value, such as the 3-dB bandwidth method [2, 54]:

\(Q=\left({f}_{i}/\Delta {f}_{3db}\right){|}_{{f}_{i}={f}_{s}\, or\, {f}_{p}}\)
(5)

and the phase derivative of impedance [54]:

\(Q=\frac{f}{2}|\frac{d\varphi }{df}{|}_{f={f}_{i}}\)
(6)

For practical applications, both the kt2 and the Q should be as large as possible. To decrease the energy loss in the resonator is helpful to increase both quantities above. From Eqs. (5) and (7), the kt2 could be a trade of the Q [54] with increasing frequencies. A high resonance frequency is beneficial to obtain a high Q, but it might reduce the kt2. Therefore, a figure of merit (FOM) as the product of kt2 and Q is introduced to measure the performance of a resonator [21].

Other performance parameters should also be considered, such as the TCF [21], which shows a temperature drift of frequency:

\(TCF=\frac{1}{{f}_{p}}\frac{\partial {f}_{p}}{\partial T}\)
(7)

where T denotes temperature. A low magnitude of the TCF is required for temperature stability of the resonant frequency [11]. This quantity is determined by the piezoelectric layer and the layers deposited on it, and its magnitude is mainly dominated by the change of elastic constant under varying temperatures [57]. Most materials possess negative TCF, while SiO2 shows a positive one. For the BAW-SMR, using the SiO2 in the reflector also has a compensation effect for the resonator TCF [2]. Additionally, the dielectric constant influences the resonator impedance which impacts the resonator size. A high thermal conductivity helps to improve the power handling capacity of the resonator [21].

4 Filter topology

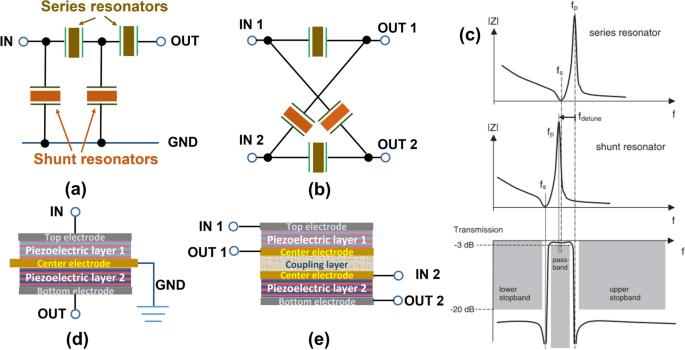
In addition to the resonator performance, the topology of the filter circuit also affects the filter characteristics [58]. The ladder- [59] and lattice-type [60] circuits are two common filter topologies for both the SAW and BAW resonators, and they are presented in Fig. 2a and b, respectively. The ladder-type has two groups of resonators with different frequencies: series and shunt ones. The shunt resonator has a lower frequency with its fp matches to the fs of the series resonator. The working principle of the ladder-type filter is shown in Fig. 2c [21]. The tuning of the resonance frequency is mainly performed by mass loading, such as using a thicker top electrode [61, 62]. The lattice-type filters also have two groups of resonators, where one group behaves capacitively and the other presents inductively [58]. The ladder-type has steep skirts but performs unsatisfactorily for rejecting undesired bands. On the contrary, the lattice type is effective for rejecting undesired bands but shows a slow slope near the passband [63]. Many attempts have been made to enhance the filter performance. For instance, a combined ladder-lattice topology was proposed to take advantage of both networks [63]. To increase the out-of-band rejection of the ladder type, additional input/output bonding wires were introduced [64]. Auxiliary inductors were also adopted to modify the lattice type for a large bandwidth [58]. Besides the ladder and lattice types, stacked crystal filter (SCF) [65, 66] and coupled resonator filter (CRF) [67] were employed for the BAW resonators, corresponding structures are presented in Fig. 2c and d, respectively. The SCF is constructed by multilayers of piezoelectric and metal films, thus it possesses the advantages of small size and low insertion loss. Based on the SCF, the CRF reduces the coupling between the neighboring vertical resonators by introducing a coupling layer, and its bandwidth is twice of corresponding SCF [18]. For the SAW resonator, different designs were also reported, such as double-mode SAW resonators [68], transversely coupled resonators [69], composite longitudinal mode resonators [70], longitudinally-coupled double mode SAW [71], and others. Generally, a filter with wide bandwidth, steep skirts, and high out-of-band rejection is desirable.

Fig. 2
figure 2

a The ladder-type filter, b the lattice-type filter, c the working principle of the ladder filter, adapted with permission from Ref. [21], d the stacked crystal filter (SCF), and e the coupled resonator filter (CRF)


5 AlN and its alloys

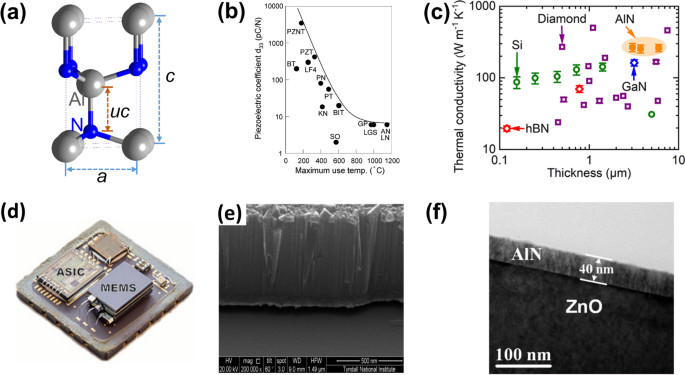
As mentioned earlier, the AlN is an ideal piezoelectric material for high-frequency filters. Its properties, synthesis methods, and alloys are elaborated here. The unit cell of AlN is shown in Fig. 3a, which is a wurtzite structure with a space group of P63mc (No. 186). Lattice parameters in the horizontal plane, a, and along the z-axis, c, were determined to be 3.11 and 4.98 Å. c/a ratio, and internal parameter u were reported as 1.60 and 0.387, respectively [72, 73]. These two structural quantities were adopted to estimate the piezoelectric performances of wurtzite materials [74]. Since the polarization of AlN is mainly along the z-axis, e33 and d33 are the largest elements respectively in the piezoelectric stress and strain matrices. Corresponding values were measured as 1.55 C/m2 and 5.50 pC/N, respectively [75, 76]. The d33 is smaller than those of other common piezoelectric materials as shown in Fig. 3b [38]. The \({k}_{33}^{2}\) of AlN was determined in the range of 6–7% [77], which is also lower than those of ZnO [33, 78] and PZT [34, 79]. As discussed before, the kt2 determines the filter bandwidth, thus attempts have been devoted to increasing this value [38, 80].

Fig. 3
figure 3

a The AlN unit cell, b relationship between d33 and the maximum use temperature for some common piezoelectric materials. BT: BaTiO3; PZNT: 0.92Pb(Zn1/3Nd2/3)O3-0.08PbTiO3; LF4: (K0.44Na0.52Li0.04)(Nb0.86Ta0.10Sb0.04)3; PZT: Pb(Zr0.52Ti0.48)O3; PN: PbNb2O6; PT: PbTiO3; KN: KNbO3; BIT: Bi4Ti3O12; SO: SiO2; GP: GaPO4; LGS: La3Ga5SiO14; LN: LiNbO3; AN: AlN. Adapted with permission from Ref. [38]. c Relationship between in-plane thermal conductivity and film thickness for different high thermal conductivity materials, adapted from Ref. [81] under the terms of the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 License. d Integrating MEMS and CMOS, adapted from Ref. [82] under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 Unported License. e Micrograph SEM of an AlN/Si film, adapted with permission from Ref. [83]. f TEM image of an AlN film, adapted with permission from Ref. [84]


Although the kt2 of AlN is unsatisfactory, many other properties ensure its superiority for high-frequency filters. As shown in Fig. 3b, the AlN presents the highest thermal stability. The maximum use temperature of AlN is higher than 1150 °C [31, 38, 85, 86]. Additionally, the AlN film presents high in-plane thermal conductivity as shown in Fig. 3c. The thermal conductivity at room temperature approximates 260 Wm−1 K−1 [81]. These thermal properties enable the AlN film’s application in high-frequency filters because the filter operation normally accompanies significant heat generation. The AlN shows a wide bandgap of 6.0 eV [87], and its electrical resistivity is as high as 1011Ω⋅m [30]. This high electrical resistivity is suitable for high-power applications. Young’s modulus of AlN approximates 340 GPa [88], and the corresponding velocities of the longitudinal and shear waves are 10,908 and 5571 m/s, respectively [57, 89]. The strong mechanical strength and high acoustic velocities facilitate the design of high-frequency resonators since the resonance frequency is proportional to the acoustic velocity as shown in Eqs. 1 and 2. With a crowed frequency band, the TCF is also an important parameter for filter selectivity and inserting loss [89]. The TCF of the AlN-based BAW was determined to be -26 ppm/°C, and its magnitude was further decreased below 3 ppm/°C by using over-moded acoustic reflector layers [90]. The advantage of AlN also lies in its compatibility with the CMOS technology, because the AlN film can be deposited by magnetron sputtering at low temperatures (< 400 °C) and its elements do not cause contamination to silicon chips [91]. Figure 3d shows an integration of MEMS and CMOS, which allows more functionalities [82]. More advantages of AlN for the filters were presented in some previous reports [21, 32, 91, 92].

Different approaches have been adopted to synthesize the AlN film, such as chemical vapor deposition (CVD) [87, 93], reactive magnetron sputtering (RMS) [94], pulsed laser deposition (PLD) [95], atomic layer deposition (ALD) [84], and others [96]. The CVD generally requires a reaction temperature higher than 700 °C [93], which is not compatible with the CMOS technology. The RMS is the widely used method, and the morphology of synthesized AlN depends on experimental conditions, such as lattice and thermal expansion mismatch between substrate and the AlN film, roughness of substrate surface, substrate bias, material and temperature, sputtering pressure, plasma power, N2 flow concentration, oxygen content, and target to substrate distance. A substrate with low lattice and thermal expansion mismatch with the AlN crystal, and a smooth surface is ideal. Based on a Mo substrate, crystal orientation is significantly dependent on the plasma power, and the optimum value for a high intensity of the (0002) orientation was determined to be 300 W. It is crucial to decrease the oxygen content because it influences the grain size of AlN. A high oxygen content could induce an amorphous structure [97, 98]. Based on the radio-frequency (RF) sputtering, the optimal substrate temperature for the (0002) orientation AlN film was determined to be 400 °C for the Mo substrate. However, the film orientation from the direct-current (DC) sputtering was different [99]. Based on a sapphire substrate, the RF sputtering weakened the lattice mismatch between the AlN and sapphire by forming a buffer layer. The (0002) orientation of the AlN film is more prominent with the N2 flow ratio of N2/(N2 + Ar) increased up to 70% [100]. The substrate temperature and bias also significantly influenced the film orientation [101]. For the DC sputtering and with a Si (111) substrate, a lower sputtering pressure and a shorter distance from the target to the substrate are conductive for synthesizing the (0002) orientation AlN film. The optimal experimental conditions for the synthesis of AlN are still yet to be investigated since the AlN morphology is influenced by different experimental parameters and these parameters are mutually coupled. The piezoelectric performance of AlN depends on the degree of (0002) orientation [102], a single-crystalline structure could have better performance than a poly-crystalline one [37]. The AlN from the RMS is generally poly-crystalline, although the intensity of the (0002) peak can be increased by optimizing the experimental parameters. A SEM micrograph of the poly-crystalline AlN from the DC-RMS approach is shown in Fig. 3e [83]. The PLD and ALD approaches were adopted to synthesize the single-crystalline AlN film [84, 95, 103], and the synthesis process was performed under low temperatures. A TEM picture of single-crystalline AlN film from the ALD is shown in Fig. 3f [84]. Although the single-crystalline structure could increase the piezoelectric performance, the synthesized AlN film is still in small size and thickness up to date [103].

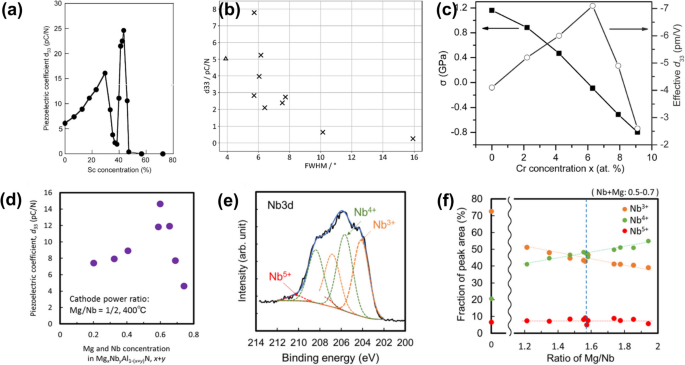
Apart from the efforts to obtain high-crystal-quality AlN films, alloying AlN with other elements was also found effective in enhancing the piezoelectric performance. Scandium (Sc) was first alloyed into the AlN lattice by an RF-co-sputtering method in 2009. The Sc concentration was controlled by the powers on Al and Sc targets. The relationship between d33 and the Sc concentration x of ScxAl1-xN is shown in Fig. 4a. A high d33 of 27.6 pC/N was obtained at the x of 43% [38]. The kt2 for the longitudinal acoustic mode increased from 7 to 10% with x in the range of 0 ≤ x ≤ 0.3 [77]. The Sc0.12Al0.88N configuration was utilized in the TFBAR, which showed a kt2 of 7.3% and a Q value of 650 [104]. Meanwhile, d31 for a transverse mode and \({k}_{15}^{2}\) for a shear mode also increased with the decrease of Young’s modulus [105, 106]. With a higher x, the hexagonal ScxAl1-xN was transformed into a cubic phase [38, 107]. The ScxAl1-xN has been extensively studied in recent years, and the filter performances based on it have been further enhanced [108,109,110,111]. Similar to the Sc, other rare-earth elements were also adopted to increase the d33 of AlN. For instance, ErxAl1-xN was synthesized by the RMS method, where an ErAl alloy target was used. d33 of Er0.0623Al0.9377N was almost twice that in the pristine AlN [112]. The d33 of YbxAl1-xN increased till x = 0.33, and a value of 12 pC/N was reported [113]. Y alloying also increased the piezoelectric constant, but the magnitude of d33 significantly depended on the samples [114, 115]. Figure 4b shows the relationship between the d33 and the full width at half maximum (FWHM) of synthesized Y0.09Al0.91N samples, which implies that a low FWHM is a necessary but not sufficient condition for obtaining a high d33. A recent work determined that the Y0.2Al0.8N presented a d33 of 12 pC/N [116]. Besides the scarce and expensive rare-earth element, other earth-abundant transitional metals (TMs) were also adopted. Cr was alloyed into the AlN by a DC-co-sputtering method as early as 2009, where several Cr chips were added uniformly on the Al target [80]. The d33 of Cr0.063Al0.937N increased 73% compared to that of the pristine AlN. Corresponding relationships between Cr concentration x and d33, and x versus residual stress are provided in Fig. 4c. The stress decreased significantly with the increasing x. The increased slope of d33 was larger than that in ScxAl1-xN, but the enhancement of d33 in CrxAl1-xN only appeared at low x. Similar to the behavior in Cr, the d33 increased in MoxAl1-xN with x up to 0.0346 [117]. Other TMs such as Ti [118, 119], Mg [120], Ta [121, 122] and V [121], were also investigated. The enhancement of d33 in TMxAl1-xN generally appears at a low x, although the d33 of some TMxAl1-xN outperforms that of ScxAl1-xN at the same x. The Ti and V alloys were determined to show lower piezoelectric constants than that in the AlN. Further, the piezoelectric performance of the AlN co-alloy of double TMs was studied. MgxTMyAl1-(x+y)N (TM = Ti, Zr, Hf, and Nb) were found to present higher d33 than the pristine AlN [123,124,125,126]. Figure 4d shows the relationship between the alloying content x + y and d33 of MgxNbyAl1-(x+y)N. A high d33 value of 15 pC/N was determined at Mg0.2Nb0.4Al0.4N. This value was further optimized to 22 pC/N by changing the x/y ratio to 1.6. In the MgxNbyAl1-(x+y)N alloy, the Nb presented different chemical states which changed with the x/y ratio as shown in Fig. 4e and f [125]. Co-alloying double TMs is an effective approach to replace the Sc alloy for enhancing the piezoelectric performance. All these alloys were synthesized by the RMS method, although different types of targets were employed [38, 80, 127, 128].

Fig. 4
figure 4

a d33 of ScxAl1-xN with increasing x, adapted with permission from Ref. [38]. b d33 as a function of full width at half maximum (FWHM) of synthesized Y0.09Al0.91N samples, adapted with permission from Ref. [114]. c Residual stress and d33 of CrxAl1-xN films, adapted with permission from Ref. [80]. d d33 of MgxNbyAl1-(x+y)N as a function of x + y at the x/y ratio of 0.5, e spectrum of Nb 3d orbitals in the Mg0.39Nb0.25Al0.36N configuration, and f presents the dependence of peak area fraction of Nb3+, Nb4+ and Nb5+, on the x/y atomic ratio, adapted with permission from Ref. [125]


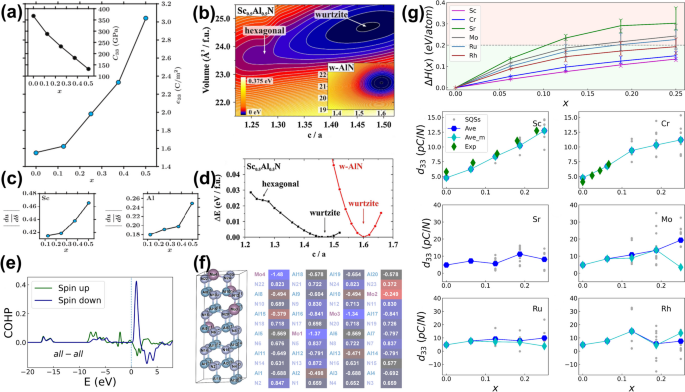
Theoretically, the significant enhancement of d33 in ScxAl1-xN was explained by the increased response of internal parameter u to applied strain ε, du/dε, and the softening of c33. Corresponding c33 and du/dε with increasing x are presented in Fig. 5a and c, respectively. The origin was assumed as a flattening of the potential energy landscape [129, 130], as shown in Fig. 5b and d. The smaller c/a ratio implied a higher piezoelectric constant [74, 129]. Further, a volume-matching condition was proposed for selecting the parent binary nitrides for alloys with high piezoelectric performance [131]. The increase of d33 in TaxAl1-xN was explained by a bond rotation mechanism [122, 132], in which the bond lengths were slightly influenced but the bond angles were significantly changed under an electric field. This mechanism could also be classified as the increase of du/dε. The increase of du/dε and elastic softening was also the origin of the d33 enhancement in CrxAl1-xN and YbxAl1-xN. Yb-Yb pair interaction contributed to the elastic softening [75, 133]. Numbers of TMxAl1-xN configurations were determined to present higher piezoelectric performance than the pristine AlN [134]. Relationships between the type and distribution of TM and the d33 of TMxAl1-xN were also discussed [135]. Both the group number and periodic number of TM impacted the d33, especially for the former. The group number of TM is correlated with its valence electron configuration. The TM with more non-bonded valence electrons prefers five-fold coordination rather than four-fold of Al in AlN, which increases the u and du/dε. Due to its nonbonded electrons, TM located in neighboring sites would bond to each other, which weakened the piezoelectric constant. The bonding behavior could be seen from the crystal orbital Hamilton population (COHP) of Mo-Mo dimer in MoxAl1-xN shown in Fig. 5e. The periodic number of TM correlates with its ionic radius. Each atom contribution to d33 in TMxAl1-xN was depicted by an effective displacement-response internal-strain parameter [136]. As shown in Fig. 5f, the same element could present diverse contributions to the piezoelectric performance due to their different positions. Figure 5g presents the mixing enthalpies ΔH(x) and d33 for TMxAl1-xN (TM = Sc, Cr, Sr, Mo, Ru, and Rh). At the same x, the ΔH(x) and d33 varied markedly between different special quasirandom structures (SQSs). For the MoxAl1-xN, the configuration with more Mo atoms in dimer or located in lines along the z-axis generally shows a low d33. Moreover, both the du/dε and c33 were found to correlate with u, and the dependence between du/dε and u was determined to be more prominent. From above, all the valence electron configuration, distribution, and ionic radius of TM could influence the stability and piezoelectric performance of TMxAl1-xN.

Fig. 5
figure 5

a e33 and c33 of wurtzite ScxAl1-xN. b Function of c/a and volume for both wurtzite and planer hexagonal Sc0.5Al0.5N. c du/dε of Sc and Al sites with increasing x in ScxAl1-xN. d Function of c/a and energy difference for both wurtzite and planer hexagonal Sc0.5Al0.5N, adapted with permission from Ref. [129]. e Crystal orbital Hamilton population (COHP) of a Mo-Mo dimer in MoxAl1-xN, adapted with permission from Ref. [135]. f A special quasi-random structure (SQS) of Mo0.167Al0.833N. The right part shows the corresponding effective displacement-response internal-strain parameter for each atom, adapted with permission from Ref. [136]. g Mixing enthalpies ΔH(x) and d33 for TMxAl1-xN (TM = Sc, Cr, Sr, Mo, Ru, and Rh), adapted with permission from Ref. [135]


Co-alloying double TMs provides more room for regulation. MgxTMyAl1-(x+y)N (TM = Ti, Zr, and Hf) was theoretically investigated, and the larger ionic radii of TM were demonstrated to contribute to the increase of piezoelectric performance [137]. The weaker TM-N bonds in MgxTMyAl1-(x+y)N (TM = Ti, Zr, Hf, Nb, Cr, Mo, and W) were determined to be one origin of the elastic soften, and which further increased the d33 [138, 139]. For TM1x/2TM2x/2Al1-xN (TM1 = Ti, Zr, Hf; TM2 = Mg, Ca, Zn), the energy difference between zinc-blende and layered hexagonal phases of TM10.5TM20.5N was found to be a good descriptor for searching alloys with high piezoelectric performance [140]. Lix/3TM2x/3Al1-xN (TM = Ti and Zr) was predicted to show a larger piezoelectric constant than AlN [141]. From a high-throughput prediction, many double-TM-alloying AlN were also found to show higher piezoelectric performances [142]. The increase of d33 generally accompanies the decrease of c33. However, it is crucial to increase both piezoelectric constant and mechanical strength for high-frequency applications [130], and which might be realized based on the tunable valence electrons, ionic radius, distributions, and relative atomic ratios between different TMs. Co-alloying Y and B were predicted to increase both the d33 and c33 of AlN [143].

6 Electrodes and substrates

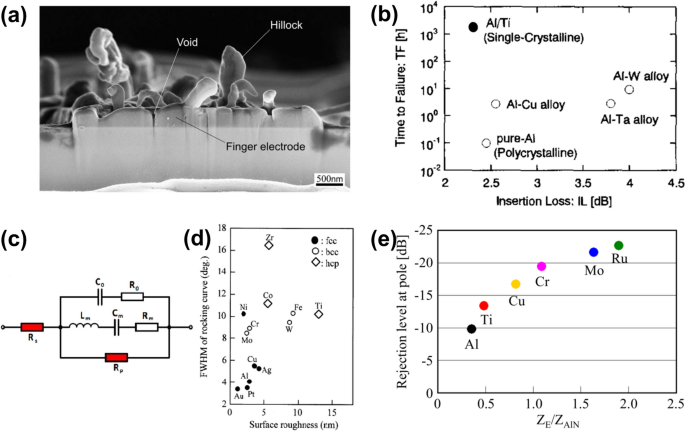
For the SAW and BAW resonators, electrodes and substrates also significantly influence the resonator performance. The widely used electrodes and substrates are discussed. Regarding the SAW, insulative substrates are often adopted [144]. Silicon [145, 146] and sapphire [147,148,149,150] are the two commonly used substrates. Other insulative substrates were also reported, such as 6H silicon carbide (6H-SiC) [151], diamond [152], silicon dioxide (SiO2), and polysilicon [153]. The silicon is widely used because of its low cost and compatibility with the CMOS technology [145]. The sapphire substrate is suitable for high-temperature applications [154]. The diamond shows high mechanical strength and thermal conductivity. It can enhance the SAW phase velocity and the capacity for heat dissipation. Deposition of diamond on ScxAl1-xN was also proposed to solve the problem of low crystal quality of ScxAl1-xN deposited on the rough surface of synthesized diamond [155]. SiO2 was used to improve the temperature stability of the resonator because its positive TCF can be used for temperature compensation to the negative TCF of the piezoelectric layer [156,157,158]. The lattice and thermal expansion mismatch, and surface roughness are critical concerns of substrates for synthesizing high-crystal-quality piezoelectric layers. The electrode (IDT for SAW) is deposited on the top surface of the piezoelectric layer. To reduce insertion loss, the electrode should have low electrical resistivity, low density, and large acoustic-impedance mismatch to the piezoelectric layer (acoustic impedance \(Z=\sqrt{\rho \times Y}\) with ρ and Y are density and Young’s modulus, respectively) [159]. A lower electrical resistivity implicates lower ohmic loss and less heat generation. A low density can reduce the mass loading effect which decreases the phase velocity of the resonator [150]. Although the decrease in electrode thickness can reduce the mass loading, it accompanies high electrical resistance and reduced thermal stability. The large acoustic-impedance mismatch could confine the mechanical energy in the piezoelectric layer [159, 160]. Considering the density and acoustic impedance, an electrode with light density and high mechanical strength is desirable. Due to its lightweight and high electrical conductivity, Al was widely adopted as IDT for the SAW [145]. For practical applications, the Al electrode suffers repetitive stress which could cause the migration of Al atoms to form voids and hillocks, especially for high-frequency operation conditions [161]. The voids and hillocks in the damaged Al electrode are shown in Fig. 6a. To enhance power durability, improvements on the Al electrode are performed, such as using a single-crystalline rather than a polycrystalline structure [162], Al alloys (CuxAl1-x [163], TixAl1-x [164] and WxAl1-x [165]), and using multilayer structures (CuxAl1-x/Cu/CuxAl1-x [166] and CuxMgyAl1-x–y/Ti/CuxMgyAl1-x–y/Ti [167]). The electrode of Al/Ti which is composed of a single-crystalline Al and a thin Ti adhesion layer shows low insertion loss and high-power durability. The performance of Al/Ti is compared to those of other electrodes in Fig. 6b [161]. The electrode with metals beyond Al were also tested for harsh environments, such as Au/Ti [168], Pt, Pt/Ti and Pt/Ta [169], RhxPt1-x [170], RhxIr1-x [171], Pt/Al2O3 [172] and TaxSiyN1-x–y/Cu/ TaxSiyN1-x–y [173].

Fig. 6
figure 6

a A damaged Al electrode with voids and hillocks in a SAW resonator, adapted with permission from Ref. [173]. b Relationship between time to failure (TF) and insertion loss of the SAW filter with different electrodes, adapted with permission from Ref. [161]. c Modified Butterworth-Van Dyke (mBVD) equivalent circuit model for BAW resonators, the electrode-induced ohmic and viscous loss (mass loading effect) was depicted by additional Rs and Rp, respectively. Adapted from Ref. [174] under the terms of the Creative Commons Attribution 3.0 license. d Relationship between surface roughness of metal electrodes and FWHM of synthesized AlN thin films, adapted with permission from Ref. [175]. e Relationship between the acoustic impedance of electrode and rejection level of FBAR filters, adapted with permission from Ref. [159]


Regarding the BAW resonator, it also requires an electrode with low electrical resistivity, low density, and large acoustic-impedance mismatch to the piezoelectric layer [159, 176]. The role of electrical resistivity and mass loading effect of the electrode could be depicted by additional resistivities based on the modified Butterworth-Van Dyke (mBVD) equivalent circuit model [174, 177] as shown in Fig. 6c. The relationship between the resonator performance and the electrode resistivity was also analyzed from measured surface vibration and finite element modeling [178]. The bottom electrode is one of the most important elements for the BAW resonator, since it not only feeds the electric field combined with the top electrode and confines the mechanical energy in the piezoelectric layer, but also acts as a substrate for the synthesis of the piezoelectric layer [176]. Fifteen metal films (Ag, Al, Au, Co, Cr, Cu, Fe, Mo, Nb, Ni, Pt, Ti, W, Zn, and Zr) were tested as the bottom electrode for the AlN film. A corresponding relationship between the FWHM of synthesized AlN film and the surface roughness of electrodes is provided in Fig. 6d [175]. The metal electrodes with face-centered cubic (fcc) lattice were determined to facilitate the synthesis of AlN with high crystal orientation, especially for the Au, Pt, and Al. However, the Pt and Au electrodes are normally difficult to deposit on the substrates directly, and Ti and Cr adhesion layers are often used together. The Al electrode suffered a low acoustic impedance for high-frequency applications [159]. Due to its low electrical resistance, high acoustic impedance, low density, and low cost, Mo is one commonly used electrode for aluminum nitride and its alloys [159, 179]. The relationship between acoustic impedance and rejection level at the pole for the Mo and other electrode materials is presented in Fig. 6e [159, 180]. The Mo and Ru show better performance. Although Mo has a lattice mismatch with the AlN and its alloys, the crystal orientation of the piezoelectric layer could be improved by using an AlN seed layer [108, 181,182,183]. Besides the Mo, the Pt [184], Ru [159], and Ir [176] electrodes were also determined to show favorable performances for the BAW resonator. Moreover, graphene and carbon nanotubes were attempted as electrodes due to their low density and high acoustic impedance [174, 185]. Transparent indium-tin oxide was also utilized as electrodes for achieving transparent electronic devices [186]. Additionally, it is worth noting that the materials for the top and bottom electrodes of the BAW resonator could be different [184].

7 Conclusion

In summary, we have briefly reviewed the research progress in AlN-based SAW and BAW resonators for bandpass filters. The resonance frequency of SAW is determined by the spatial periodicity and the acoustic velocity, and that for the BAW is dependent on the thickness of the piezoelectric layer and the acoustic velocity. The BAW is more suitable for high-frequency applications. Regarding the characterization of resonator performance, the kt2 and Q are two key parameters, which respectively determine the filter bandwidth and selectivity. The TCF is also important for temperature stability. The ladder- and lattice-type topologies are two common types of filter circuits. More advanced filter topologies are also proposed for achieving wider bandwidth, steeper skirts, and higher out-of-band rejection. For the piezoelectric layer of the resonator, the advantages, synthesis methods, and piezoelectric performances of AlN and its alloys are highlighted. Increasing the kt2 is the main concern for the AlN film. The synthesis of AlN in single-crystalline or poly-crystalline with a high intensity of (0002) orientation, and alloying the AlN with other elements are two effective approaches. Different mechanisms have been proposed to explain the increase of piezoelectric constant in the AlN alloys. All the valence electron configuration, ionic radius, distribution, and atomic ratios of alloy elements are determined to influence the piezoelectric performance. For the substrates and electrodes, the lattice and thermal expansion mismatch, and surface roughness are critical for the synthesis of a high-crystal-quality piezoelectric layer. The electrodes with low electrical resistance, large acoustic-impedance mismatch to the piezoelectric layer, and low density are ideal to reduce the insertion loss.

Based on the research status, several possible research directions are suggested as follows: 1) to develop more advanced resonator structures and filter topologies for high-frequency, low insertion loss, and wide bandwidth filters; 2) to synthesize high-quality or single-crystalline AlN, and its alloys for achieving better resonator performances; 3) to enhance both the kt2 and mechanical strength of AlN through alloying. The original advantages of AlN for filters should be reexamined for the AlN alloys, such as the TCF and high-temperature stability. 4) To develop more advanced electrodes. With increasing resonance frequency, the thickness of the piezoelectric layer becomes thinner in the BAW resonator. More mass-less and high-stability electrodes need to be developed. 5) To control the thickness uniform of the piezoelectric layer and electrode could also be a challenge for high-frequency filters. Influences of the interfaces between the electrode and piezoelectric layer could be significant for high-frequency resonators, and they deserve further study.