Abstract
The angular distance of the solar flares to the projective point of the center of the solar disk on the solar spherical surface has been studied by the heliographical or helioprojective coordinates, during the periods 1975–2021 for GOES events and 2002–2021 for RHESSI events, hereafter “distance.” It gives a specific distribution curvature. It has also been noted that when using the number of solar flare events in each satellite, GOES or RHESSI, or even using the sum of the flux (class) or importance parameter, it obtains the same result, which is that the shape of the distribution curve remains in its shape without any significant change. In addition, it has been shown that the distribution curve contains a specific number of peaks. These peaks have a specific distance from the center of the solar disk that is very similar to the projection of the solar interior layers on the solar disk. For this reason, the names of these four main peaks have been given as follows: (1) the core circle (0–15°): it is a projection of the solar core onto the solar disk, (2) radiative ring (15–45°), and (3) the convection ring (45–55°). The limb ring is 80–90°. This result makes us wonder why the number of events in the middle of the solar disk is few, and also small at the solar limb, while many in the other parts in the solar disk. This suggests that we need to understand the sun better than before, and it also suggests that solar flares are connected to each other through the solar interior layers, the extent of which may reach the convection zone or perhaps beyond that, or the opacity of the convection zone may be less than the currently estimated value.
1 Introduction
Although the gaseous nature of the sun allows its interior to be known only through models, other outer layers, such as the photosphere, chromosphere, and corona, can be observed. Most solar phenomena occur in these upper layers, such as solar flares that appear in the chromosphere and photosphere.
Previous studies of the heliographical distribution of solar flares were studied in different methods. Authors of [1,2,3,4,5,6] studied the latitudinal distribution. One of the previous studies on the solar flare’s location on the solar disk found that the solar flare’s latitude varies with the solar activity [7]. These studies found that solar flares have an almost symmetrical distribution over latitudes between northern and southern hemispheres. Most of the occurrence of them is at latitude ~15°. It may vary with solar activity [5].
On the other hand, although there is homogeneity between the northern and southern hemispheres represented by latitudinal distribution [5, 6]. Authors of [8,9,10,11,12] studied the longitudinal distribution of solar flares. The solar flares have no homogeneity between the eastern and southern hemispheres [11]. The specified longitudes may be associated with coronary mass ejections (CME) [9].
But the study of the latitudinal and longitudinal distribution together was done recently by [6], and that this mixed distribution concluded that the solar flares occur at a specific latitude called the eruptive latitude [6]. Most solar flares occur near or within active regions. This is because these solar flares need magnetic energy.
Studying the heliographical distribution of solar flares is very important, as it may affect space weather, the Earth’s magnetic field and its ionospheric layers [13]. It is also one of the main sources of coronal mass ejections. Knowing the location or distribution of the solar flare contributes to knowing the direction of the coronal mass ejections accompanying it [14, 15], which contributes to knowing whether it may reach Earth or not.
The different layers in the sun can only be seen under certain conditions or in certain wavelength bands, except for the innermost layer of the sun’s atmosphere, which is called the “photosphere.” It is the layer where most of the sun’s energy is, and it is always seen. We can observe it directly. Despite being the highest layer, the corona cannot be seen directly. It can be observed during a natural or artificial solar eclipse, which blocks the light of the photosphere. But is it possible to observe the inner layers of the sun, such as the solar core? Is it possible to observe the impact of the inner layers on the solar surface?
The produced energy in the solar core must pass through large amounts of plasma to reach the solar surface, where it is radiated away in mainly two ways: radiation and convection. Solar energy transport switches from radiation to convection. The transmission of this energy from the interior to the photosphere and the appearance of interior layers depend on the opacity of the convection zone. Geometrically, we can see the inner layers of the sun if the convection zone has a transparency. This is because that the direction of the observer penetrates the inner layers of the sun. Unfortunately, the models give high opacity for the convection zone [16]. So those inner layers cannot be seen. Modern studies such as [17, 18] have been used in helioseismology as an indication of what is inside the sun. Helioseismology gives lower opacity than previous models, such as the Dynamo model. All of these previous studies indicate that solar flare is a surface event, not related to the inner layers of the Sun. On the other hand, the opacity is a complex quantity that depends on myriad detailed radiative processes, primarily bound-bound transitions and bound-free transitions (photoionization), as well as the chemical composition and the equation-of-state of plasma in the solar interior [19, 20]. Also solar flare events some time appeared in two locations at the same time. This case is called “sympathetic solar flare.” About 80% of sympathetic flares have the same class and energy approximately [21]. This study found that the angular distance between both sympathetic flares may reach to ~90°, which means that there is a physical connection between both flares [22] and may reached through solar inner layers.
Accordingly, there is no previous study that addressed the angular distance from the center of the solar disk to the position of the solar flare, which resembles or mimics the inner layers of the sun.
In this study, I will study the angular distance of the solar flares from the center of the solar disk by different coordinate systems, during different solar activity cycles, and with comparing different X-ray bands using GOES and RHESSI satellites which are located in different locations in the interplanetary space.
This study is significant to understanding whether it is solar flare position distribution, it is just a similarity to the solar inner layers, or an understanding the distribution of the solar flare events on the solar disk.
1.1 Distance distribution
The sun is a gaseous sphere, so it has specific coordinates that can be used to distinguish between different events on its surface, and track their positions and paths. The most famous of these coordinates are the heliocartesian coordinates (X, Y), where the point (0, 0) refers to the center of the sun’s disk and the direction of the observer itself (i.e., Earth direction). These coordinates are the easiest to measure and can be estimated easily through images of the solar disk. They can also be converted into helioprojective coordinates (longitude, latitude), which may be called heliocentric coordinate systems, but they still rely on the direction of the observer (i.e., Earth or satellite direction too), which is represented by a latitude of 0. The sun is not stationary; it rotates around its axis and has a tilt that changes over time. Therefore, the north and south poles of the sun change their positions on the solar disk over time and can be located in behind or in front of the solar disk. The same goes for the solar equator, which varies its position with time and is not a straight-line path on the center of the solar disk. The true equator may differ from the middle of the sun’s disk. The true coordinates of the sun are called heliographical coordinates. In addition, it is possible to convert between different coordinate systems [23, 24].
Any point on the spherical surface such as the sun is determined or specified by spherical coordinate systems (i.e., in three dimensions that are denoted by latitude, longitude, The third axis is the solar radius, which is equal to unity, so it is ignored) such as heliographical or helioprojective coordinate systems. But this sphere and its surface’s points appear as a circular disk in an image, which is specified by a two-dimensional system (X, Y, or distance from the center of the solar disk d). Therefore, we can create a new distribution based on the distance of the solar flare from the center of the solar disk (d), which is represented by angular distance on the surface of the sun in the spherical coordinates (latitude and longitude). This distance can be measured as an angle in spherical coordinates.
The heliographical or heliocentric (helioprojective) coordinate systems depend on the observer’s direction. These coordinate systems, each of them has a different center of solar disk than the other, because there are see the sun from a different perspective. But the distance is still unique and is not affected by the sun’s tilt or by changing coordinate system. It may yield new results that have not been studied before.
To calculate the angular distance of the solar flare, whatever type of spherical coordinate is used, we need to represent the sun as in spherical, and plane or circular coordinates, and then develop a mathematical method to convert between them.
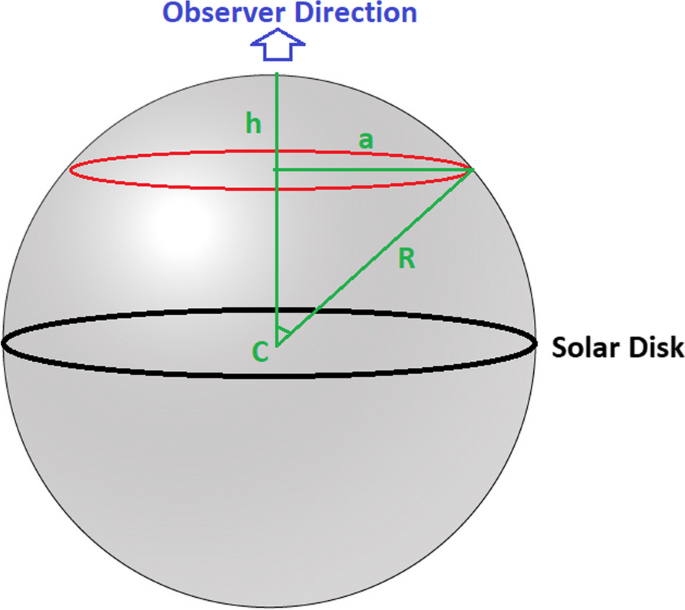
As we can see in Figure 1A of the horizontal sector of the sun, we have random solar flare points (denoted to F) on the spherical surface of the sun. The point of the solar flare has an image or projection in the solar disk in the background or in front flat plane (i.e., represented to the solar disk) that is tangent to the solar sphere at the center point of the solar disk (denoted to F′), after penetration of the inner layers of the sun, while Figure 1B represents a vertical sector of the sun. It demonstrates a random location of solar flares on the solar disk (turquoise, blue, light-blue, and black points represented by stars). All these points have different latitude and longitude, but the above represents a specified inner layer (different depths) according to the observer direction. The line from these points to the center of the circle (center of the solar disk) is the distance which our study is concerned with.
Plot (A): Equatorial and latitudinal sectors of the Sun (horizontal sector). The green circle represents the solar latitude. The black circle represents the projection of the solar latitude on the solar disk. F is the solar flare on the spherical surface. While F’ is the projection of the solar flare on the solar disk. Plot (B): The solar disk (vertical sector) of the sun. The turquoise line represents the distance D of the flare above the solar core. Consequently, it is above the rest of the inner layers. The black and indigo lines represent the solar flares above other inner layers such as radiative and convection zone layers. The purple line is the central distance of the solar flare above the solar limb. It represents the solar photosphere only
The turquoise point is the solar flare occurring above the solar core. The turquoise represents the central distance D of the flare from the center of the solar disk to the flare’s location. Consequently, this flare is above the rest of the inner layers. Black and indigo pointer lines represent the central distance of the solar flares above other inner layers such as radiative and convective zones. The purple line is the central distance of the solar flare located at the solar limb that equals 90°. It represents the surface (i.e., solar photosphere or chromosphere) only. While the angular distance is around 0° for the exact central flares. Now, we need to distribute the solar flare according to the central angular distance (hereafter, distance or D).
1.2 Distance calculation method
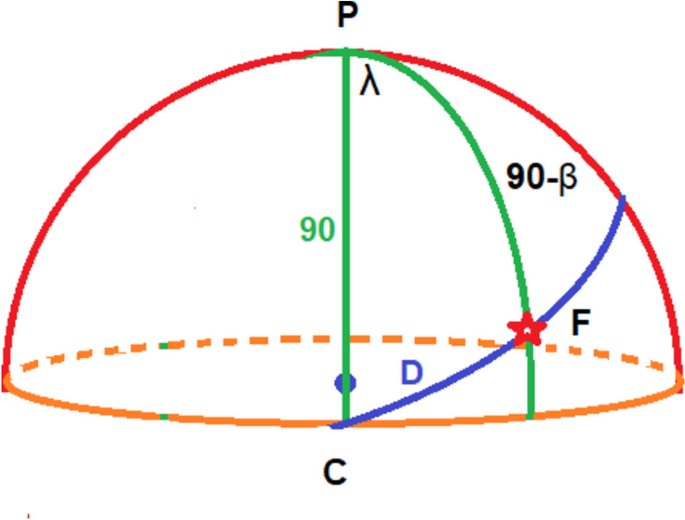
The estimation of distance is done by assuming the sun is a spherical body, using the laws of a spherical triangle, as shown in Figure 2; by applying the cosine formula, the distance can be derived by the following formula:
The spherical triangle of the projection of solar flare F on the solar surface. C denotes the center of the solar disk,. it is positioned on the solar equator (orange circle). The right green circle is a great circle that represented to the flare’s longitude passes from pole P, while the left green great circle is the central meridian of the sun. The arc 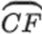 is the angular distance between the center of the solar disk and the flare
is the angular distance between the center of the solar disk and the flare
where D is the flare’s distance between the projection point of the center of the solar disk on the surface of the solar sphere and the solar flare position by any coordinate systems such as heliographical or helioprojective coordinates. \(\lambda\) and \(\beta\) are the flare’s latitude and longitude, respectively.
We can divide the distance into 90 slices (intervals) to give us a higher accuracy (i.e., 1° interval). This range will be 1–90°. The smallest circle is the closest one to the center of the solar disk, which simulates or represents a projection circle to the solar core. The greater circle is the projection circle that represent the limb.
We can convert cartesian coordinates (x, y) to the projective coordinates by the following formula, driven by [24]:
where \({R}_{\odot}\) is solar radius. Then we can substitute these helioprojective coordinates into Eq. 1.
2 Data sources
The X-ray solar flare data is obtained by Geostationary Operational Environmental Satellites (GOES) satellites from the URL: {https://hesperia.gsfc.nasa.gov/goes/goes_event_listings/} during the solar period 1975–2021 and by Reuven Ramaty High Energy Solar Spectroscopic Imager (RHESSI) from the URL: {https://hesperia.gsfc.nasa.gov/rhessi3/data-access/rhessi-data/flare-list/index.html}.
The GOES X-ray flux contains 1-min averages of solar X-rays in the 1–8 Å (0.1–0.8 nm) and 0.5–4.0 Å (0.05–0.4 nm) passbands [25, 26], while RHESSI solar flares [27, 28] are occasionally reprocessed (e.g., the 18 Sep 2022 update mentioned above and the 10 Sep 2010 by using the 6 to 12 keV instead of the 12 to 25 keV band).
In addition, the coordinate of the GOES solar flare is heliographical coordinates, while the RHESSI solar flares’ positions are specified by heliocartesian coordinates that need to be converted to the helioprojective coordinates Eqs. 2 and 3.
The goal of using different coordinate systems is to show whether they give the same or different results. If the results do not differ, it indicates that the result is related to the inner layers of the sun, and we will get the same result with any observer direction, because the equator in the heliographical coordinate system is not the equator in the sun’s disk, and the center of the sun is not located on the line of the equator at the solar disk, and this result leads to that the solar flares are related to the solar interior. If the distribution result differs, then location is not related to the inner side of the sun.
The GOES catalog of the solar flares already included the heliographical coordinates. We can substitute the latitude and longitude of the flares determined from GOES and RHESSI, determined by Eq. 2 and 3, into Eq. 1 to calculate the angular distance of the solar flare.
3 Results and discussions
In this study, the angular distance of the estimated solar flare from the center of the solar disk to the position of the solar flare has been studied. The number of events counted per distance unit, which equals 1°. This distribution is called “distance distribution.”
The distance was calculated for all solar X-rays (SXR) during the period 1975–2021 for heliographical coordinates obtained by the GOES catalog and for RHESSI solar flares during the period 2002–2021 for helioprojective coordinates, and then the number of events was counted per unit distance for comparison purposes.
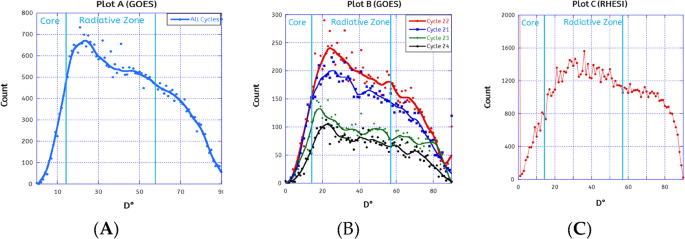
Figure 3 depicts the central distance distribution (D) of the X-ray solar flare during all solar cycles (A), each cycle (B) by the flare’s count for GOES, and (C) for the RHESSI. The result of the calculated distance for all flares during the selected period with their count of flares at all distances is presented in Figure 3A. The behavior of the distance curvature indicates clearly that the flares demonstrate the inner layers.
The central disk events are very few 0 < D < 15°. This region reflects the solar core on the inner side (i.e., it is a projection area of solar core on the solar surface). Furthermore, the number of events at the limb 80° < D < 90° is very low, reflecting only photosphere and chromosphere events, while a large number of the flares happened at a distance of about 15–20°. This region denotes the inner side of the radiative zone in inner side after the solar core’s projection, whereas the middle area 20° < D < 80° has a large number of X-ray events, and this is because this region reflects many interior layers in the background.
The data is classified by solar cycle as shown in Figure 3B, to check how solar activity affects the curvature shape. We note that the curvature shape remains the same as it is during each solar cycle (21 to 24 cycles). In addition, we can show that the peaks number can increase or decrease according to solar cycle activity.
Also, we can show about four peaks during the distance range of 0–90°. The main and higher peak (hereafter, the core peak or core circle on the solar disk) is a distance of about 15–20° that reflects the solar core. This means that the small peaks reflect other interior layers, including radiative and convection zones, which we will discuss briefly.
The core’s peak moves and changes slightly with time. We notice that the far radius is for cycles 21, 22, 24, and then 23, respectively. If this curve represents the inner layers, this means that the solar core radius increases as the strength of the solar cycle progresses and activity increases and vice versa.
It is worth noting that I repeated the same graph shown in Figure 3 but classified data according to flares’ GOES classes (B, C, M, and X). Besides, I examined the solar activity by classifying data according to quiet and active periods for all the selected periods and during each cycle. I did not get a significant result. The curvature of Figure 3 remains similar.
The plot is applied with all RHESSI solar flares as shown in Figure 3C, to check how the solar radiation bands (X-ray in the current study) and the different coordinate systems affect the curvature shape. I note that the curvature shape remains the same. But the results showed a huge number of events (about 25,000 flare events) exactly in the center of the solar disk (D = 0°) with RHESSI data, unlike those observed by GOES. This is because that the (0, 0) located flares means that these events have not a recorded coordinate in RHESSI catalog. The number of flare events that have a distance greater than 1 is about 90,000.
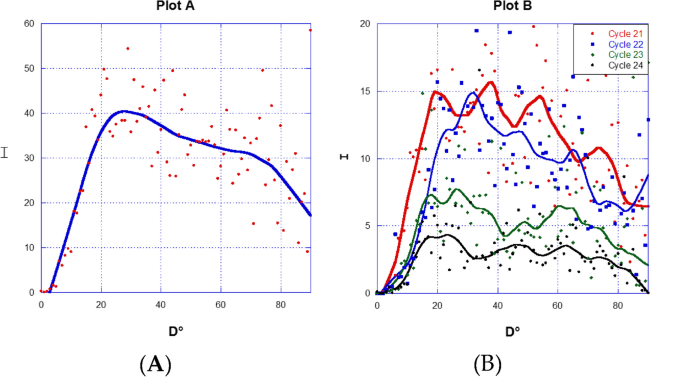
For additional confirmation of this result, we can calculate the total importance I of these GOES flares that occurred at the same distance, by following formula.
where I is the importance value of GOES solar flare. \({f}_{n}\) is worth 1 for the X-class, 10 for the M-class, 100 for the C-class, and 1000 for the B-class. n is the index of flare events that occurred at the same distance D (It is represented by one of the symbols, B, C, M, and X). \({I}_{D}\) represents the total value of solar flare importance in the X-class unit that occurred in the distance D. Figure 4 shows the compatibility of the total importance with the curvature of the number of events. But the high contrast of the curvature peaks matters more than the count of the events. It is clear that we have four peaks similar to Fig. 3.
The peaks in the distance curve may be the same as the solar inner layers, by considering that it is a projection of the inner layers on the solar disk, or they may represent something else. Therefore, we will distinguish the circles represented on the solar disk by different names inspired by the names of the inner layers, as follows:
-
The core circle: It is a projection of the solar core on the solar disk.
-
The radiative ring: It is a projection of the radiative zone on the solar disk.
-
The convection ring: It is a projection of the convection zone on the solar disk.
-
The limb ring: It is a projection of the photosphere on the solar disk.
3.1 The relationship between distance and radius
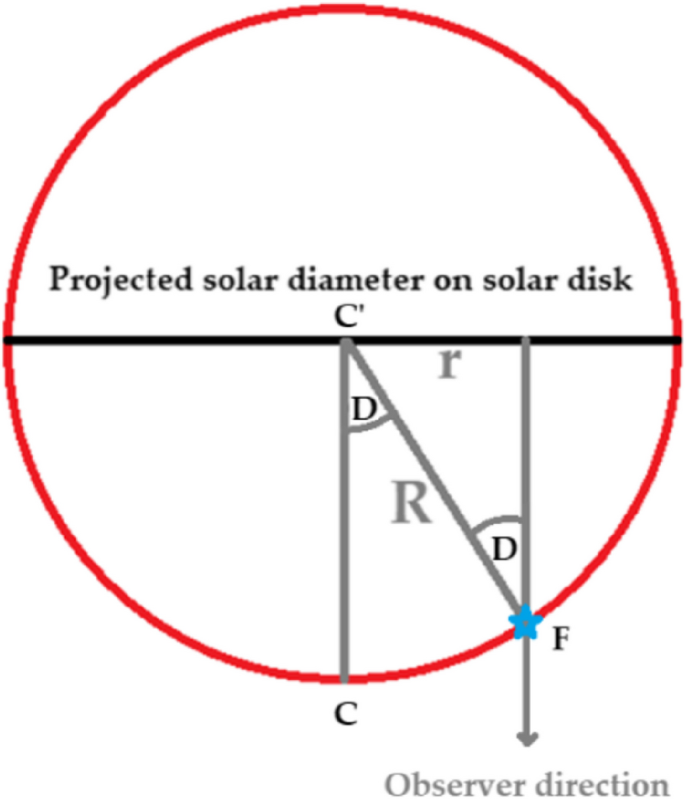
Previous studies calculated the radius of the inner layers in units of the radius of the sun \({R}_{\odot}\). It differs from the measurement method here used in this study, which reflects the inner layers of the sun. Within the scope of this study, we must convert the radius from scalar distance \({R}_{\odot}\) to angular distance D°. So that the units are unified between angular distance and depth, it will be easier to compare the current results with the previous studies. Figure 2 depicts the sun’s great circle 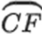 sector, which is depicted in Fig. 1. The black line is the projection of solar diameter on the solar disk. It may be the solar equator itself if the position of the solar flare is on a solar equator. The distance D of any interior layer that has a depth radius of r is given by the following:
sector, which is depicted in Fig. 1. The black line is the projection of solar diameter on the solar disk. It may be the solar equator itself if the position of the solar flare is on a solar equator. The distance D of any interior layer that has a depth radius of r is given by the following:
By putting the solar radius \({R}_{\odot}\) = 1, then
3.2 The disk rings and inner layers radius
Figures 4 and 5 show four peaks after the core’s peak, including two peaks after the convection ring. Each peak denotes a disk rings, and each has a boundary denoted by two crests. These crests appear clearly in weak solar cycles 23 and 24, especially in solar cycle 23. These peaks overlap during strong solar cycles such as 21 and 22. That longest distance demonstrates the radiative ring. The distance between the core and the radiative rings is not clear because the curve is rising sharply within the solar core.
We already know that X-rays cannot reach easily and directly from the solar core to the surface. However, the increase in the number of solar flares in the region of the core circle, which simulates the core of the sun, makes us wonder. Why? So, I will compare the radius of the solar inner layers to the angular distance of the solar flares. There may prove a correlation or not.
The solar distance of core-radiative zone boundary equals about 0.25 \({R}_{\odot}\) according to [29, 30]. According to [31], the radiation-convection boundary occurs at about 0.71 \({R}_{\odot}\). Using Eq. 6, hence as follows:
where \({D}_{c}\), \({D}_{r}\), and \({D}_{v}\) are the distances from the center to the core, radiative, and convection zones.
This result is consistent with the current results shown in Figures 3 and 4, where the 15° distance represents the core circle (peak of the core). This may indicate a connection between the rings on the solar disk with the inner layers of the sun.
3.3 The link between solar flares and solar interior layers
The similarity between the distribution of solar flares on the surface with the inner layers of the sun is interesting and unexpected, because this indicates two possibilities: either there is an indirect connection between the inner layers and solar flares or that the solar interior layers above solar core have lower opacity than expected in the past. This means that the solar flares that we see may be in the back side, which we see at the front side from the side of the observer. Because the solar flare events in the middle rings are much more than those in the center of solar disk or at the limb. This result also suggests that the sun has a strong magnetic field that dominates the surface of the sun, and its main origin is the solar core itself. This magnetic field is one of the main reasons for the formation of solar flares above the solar surface. Which indicates that solar flares are the result of the reconnection of the core magnetic field lines with each other at the surface, or with local magnetic field lines formed due to the plasma present in the active region.
The largest scale event that occurs above solar surface is the coronal hole. It is the most event that scientists believe may be linked to the solar interior, because it occupies a large area above the solar surface. Coronal holes are closely connected to large-scale solar magnetic field patterns, so the obvious link between coronal holes and the interior is through these patterns, since the magnetic field is almost certainly generated, maintained, and evolved by dynamo action in the solar convection zone. The magnetic field is most likely also the dominant link. It is possible there are weak (as yet unobserved) global scale anomalies in the thermal energy carried to the surface by solar convection, but these variations would be extremely small compared to variations in the magnetic field. Is it only convection zone dynamics which influences the surface magnetic field or could it be influenced by changes in the radiative interior? Deep interior influences seem unlikely on the time scale of a few weeks, months, or years, except perhaps from the boundary layer just below the convection zone. Otherwise, the natural time scales for the interior are much too long. Furthermore, convection zone mixing is so vigorous as to obscure any weak influence from the interior. There are several processes which probably occur in the solar convection zone that should have an influence on the patterns and amplitude of surface magnetic fields. The relative importance of these is not known, and in a nonlinear fluid system such as the convection zone, they are probably not separable from one another. These processes include the induction effects of convection and differential rotation themselves; effects of hydromagnetic and rotational wave propagation; effects of dynamo waves, random walk, or diffusion of magnetic flux by small-scale turbulence; effects of magnetic buoyancy, and field line reconnection. Sorting out how each of these processes enters determining how a particular magnetic field pattern evolves in time would be a formidable task even if comprehensive measurements of both magnetic and velocity fields existed. In fact, our knowledge of global scale velocity fields on the sun, outside of the differential rotation itself, is very limited, so the task is more difficult still. Even with knowledge of the surface global velocity fields, it does not necessarily follow that we could show that the surface magnetic field responds in a simple way to these flow patterns. The magnetic field may be influenced more by dynamics at deeper levels, which may not be the same as at the surface. All of the above processes contribute, in greater or lesser degree, to the solar dynamo. All we can hope to do in this chapter is indicate what clues are known as to the roles they play and what further clues might be looked for [32]. Previous studies may agree that solar flares may reach the convection zone and not deeper than that [19, 20]. Magnetic fields undergo some instability at the base of the convection zone. As the fields extend into the convection zone, they become buoyant and rise and determine the behavior of the outer layers of the Sun, including the corona [33, 34]. On the other hand, solar flare events some time appeared in two locations at the same time. This case is called “sympathetic solar flare.” About 80% of sympathetic flares have the same class and energy approximately [21]. This study found that the angular distance between both sympathetic flares may reach to ~90°, which means that there is a physical connection between both flares [22] and may reached through solar inner layers, which may suggest the possibility of contact deeper than the convection zone. In addition, the authors of [19, 20] concluded that the opacity is a complex quantity that depends on myriad detailed radiative processes, primarily bound-bound transitions and bound-free transitions, as well as the chemical composition and the equation-of-state of plasma in the solar interior.
3.4 Distance model
Regardless of the physical connection between solar flares and the inner layers, we will create a mathematical model that links surface events with the inner layers. The first step is to assume the solar surface is a spherical body. The projection of the solar interior layers on the solar disk appears as circles around the center of the solar disk. We can split the sun into 90 circles centralized by the center of the solar disk which appear as layers around the center of the solar disk. The suggested angular interval between these circles is 1°. We need to calculate the area of these projected circles on the real sphere on the front side and in the background, including the backside too. If we calculated it for the frontside, we could multiply it by n number to give the areas of background spheres, including the backside. The projection of the circles on the real sphere is called “segment,” which I want to estimate its area. Each segment has two boundaries of circles, upper and lower. Each circle has a central angle. θ is for the upper (far) circle, and Φ is for the lower (near) circle, which are measured from any flare’s direction (point on this circle) and the center of the solar disk (direction to the Earth in helioprojective coordinates). This solar sphere is depicted in Figure 6 in the segment where we want to estimate its area.
The schematic of the sun. C is the center of the sun and the solar disk. The black circle is the projected solar disk for the sun for the observer. The spherical cap is the upper boundary of the spherical segment of the solar flares. The difference between the areas of the upper and lower caps gives a segment area
The area of segment [35] is the difference between the boundary two caps. We can write the following:
where A is the area of the frontside segment. Ω is the angular distance of the projected circle (segment angle). Then, the area of both spherical caps, which have angles θ and (θ + 1°), becomes the following:
The segment area formula becomes as follows:
But \({R}_{\mathrm{\odot}}=1,sin\left(1^\circ \right)\approx \frac{\pi }{180}\), and \(cos(1^\circ )\approx 1\), then as follows:
Equation 15 refers to the sinusoidal function. In order to integrate this segment area over all the background layers reaching to the backside of the photosphere, the equation becomes the summation of sinusoids equation [36] that is written as follows:
where \({\mathrm{a}}_{\mathrm{n}}\) is the amplitude represented by an inner layer and \({\mathrm{T}}_{\mathrm{n}}\) are the frequencies of angles (period) in degrees. \(v\) is the offset value, and D is the distance of the solar flares count n or the summation of the importance I in X-class of all solar flares that occurred at the same distance. I set m = 3 because this is the best value for the high correlation coefficient and represents the simplest equation.
The compatibility of Eq. 16 with experimental data was investigated, and it was discovered that Eq. 16 gives a strong coefficient of determination \({R}^{2}\), as shown in Table 1. \({R}^{2}\) equals 0.97 and 0.752 for the count and the importance of the flares. The sinusoid amplitude was discovered to be greater than the value of \((2 {\pi }^{2}/180)\) in Eq. 16, indicating that there are many layers in the background added to the front and back sides of the surface.
| N | Count | Importance | ||
|---|---|---|---|---|
| A | T | A | T | |
| 1 | − 233.9 | 4.408° | − 14.84 | 4.408° |
| 2 | − 165.8 | 7.804° | − 12.13 | 7.804° |
| 3 | − 68.5 | 11.053° | − 3.895 | 11.053° |
| 428.4 | 28.82 | |||
| 0.97 | 0.752 | |||
| Chi-sq | 1.099E05 | 4059 | ||
| 1.4266E67 | 2.708E-29 | |||
4 Conclusions
I studied the angular distance of the solar flares from their position in helioprojective and heliographical coordinates to the projection point of the center of the sun on the solar disk, using the solar flares data obtained from GOES (for heliographical coordinates) during the period 1975–2021 and RHESSI (helioprojective coordinates) during the period 2002–2021. The solar disk is divided into 90 central rings. The number of solar flares that occurred in each ring was then compiled. It turns out that the results give a definite shape to the curvature of the distribution. It has also been noted that the shape of the distance distribution of solar flares remains the same with different solar activity cycles, and with the different GOES classifications. Also, distance distribution of solar flares remains the same with number of events or with importance total value. In addition, distance distribution remains with different observations’ directions. In addition, the different coordinate systems do not give any differentiation in the results. All coordinates give exactly the same distribution. This study suggests that solar flares are the result of the interaction of a magnetic field originating from the solar core, perhaps interacting with the local magnetic field in the active region. Also, the fact that the distance distribution does not vary with different coordinates suggests that the opacity of the convection zone layer is greater than previously estimated.
What reinforces this result is that it was noticed that the shape of the curvature did not change when using the overall importance value of the solar flare. But this distribution is now showing the peaks in the curve more than the distribution using the number of solar flares. There is a fixed number of peaks observed, and each cycle is present. It does, however, sway slightly with each solar activity cycle. It seems to be related to the strength of the solar activity cycle. The number of these vertices is four, which may mean that the distance distribution may reflect or be similar to the geometry of the interior of the sun. It was noted that these peaks form central rings that simulate the inner layers of the sun. So, we divided the solar disk into specific rings in line with the solar inner layers. As these loops simulate and look like the solar inner layers in the background.
These rings were divided according to the peaks in the curve as follows:
-
The core circle: It is a projection of the solar core onto the solar disk. It has solar flare distances in the range of 0–15°. This ring has very few solar flares.
-
The radiative ring: It is a projection of the radiative zone on the solar disk. It has solar flare distances in the range of 15–45°.
-
The convection ring: It is a projection of the convection zone on the solar disk. It has solar flare distances in the range of 45–55°.
-
The limb ring: It is a projection of the photosphere on the solar disk. It has a very low number of flare events. It has a range of 80–90°.
4.1 Recommendations
Based on the results of that study, which concluded that there is a distance distribution for solar flares, it maintains its shape regardless of the observer’s direction or the coordinate system of the solar flare, and it even maintains its shape with varying solar activity, which leads us to recommend the following:
-
The estimation of the opacity of the convection zone with X-ray must be reconsidered.
-
Solar events connected together by magnetic field lines through the inner layers must be studied.
-
I propose to study the same solar flare from different directions as is done with coronal mass ejections by observing it with different satellites SOHO/LASCO, STEREO A, and STEREO B. Because monitoring solar flares in this method (in three dimensions) may help determine the correction location of solar flares more accurately.


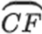 as shown in Fig.
as shown in Fig.