Abstract
Excited states are essential to many chemical processes in photosynthesis, solar cells, light-emitting diodes, and so on, yet how to formulate, quantify, and predict physiochemical properties for excited states from the theoretical perspective is far from being established. In this work, we leverage the four density-based frameworks from density functional theory (DFT) including orbital-free DFT, conceptual DFT, information-theoretic approach and direct use of density associated descriptors and apply them to the lowest singlet and triplet excited states for a variety of molecular systems to examine their stability, bonding, and reactivity propensities. Our results from the present study elucidate that it is feasible to employ these density-based frameworks to appreciate physiochemical properties for excited states and that excited state propensities can be markedly different from, sometime completely opposite to, those in the ground state. This work is the first effort, to the best of our knowledge, utilizing density-based reactivity frameworks to excited state. It should offer ample opportunities in the future to deal with real-world problems in photophysical and photochemical processes and transformations.
Graphical Abstract
1 Introduction
Crafting a density-based theory of chemical reactivity in density functional theory (DFT) [1, 2] has been our endeavor in the recent literature [3]. The current understanding of this density-based reactivity theory is that it contains four relatively independent frameworks, orbital-free DFT (OF-DFT) [4], conceptual DFT (CDFT) [5,6,7,8], information-theoretic approach (ITA) [9,10,11], and density associated quantities (DAQ) [3]. In OF-DFT, no orbital is mandatory to formulate and quantify physiochemical properties. Instead, we make use of energy density functionals and their derived quantities for the purpose. For example, Weizsäcker kinetic energy can be utilized to quantify steric effect [12]. Pauli energy was employed to define ELF (electron localization function) [13], SCI (strong covalent interaction) [14], and BNI (bonding and nonbonding interaction) [15] indexes to identify and determine both strong and weak interactions in molecules. In CDFT [5,6,7,8], chemical potential, hardness, electrophilicity index, Fukui function, dual descriptor, etc., were formulated to associate them with different chemical properties and processes. In ITA [9,10,11], simple density functionals borrowed from information theory such as Shannon entropy [16], Fisher information [17], information gain [18], etc., were utilized to quantify reactivity propensities such as electrophilicity, nucleophilicity, and regioselectivity [19,20,21,22]. In DAQ, direct uses of the electron density, its gradient, and Laplacian (e.g., QTAIM [23]) as well as their different ways of combinations, for instance, NCI (noncovalent interaction) [24, 25] and USI (ultra strong interaction) [15] indexes, were systematically pursued. A brief introduction of the formulation of these theoretical methods is included in SI. While these four density-based frameworks have achieved considerable progress in the literature, as outlined in our recent perspective article [3], we argued that several new directions should be intensively pursued, such as topological analysis [26] and exited states. In this contribution, we present our new results of applying these density-based frameworks to quantify properties for excited states.
Excited states play a key role for the properties of molecules and materials. They are closely related to photosynthesis, fluorescence, biophysics, photonics, and quantum computers. DFT is known to be a ground state theory, but its extension to excited states has long been accomplished [27,28,29]. With the establishment and implementation of Time-Dependent DFT (TD-DFT) in the literature [30, 31], routine access to the lowest singlet and triplet excited states of molecules and materials has become possible. In this work, we extend the four density-based reactivity frameworks originally developed for the ground state to deal with excited states. The purpose of our present work is two-fold. First, we demonstrate that applications of the previously established density-based reactivity frameworks to excited states are feasible and productive. Secondly, we will show that results obtained for excited states have their own characteristics, which may or may not be substantially different from those for the ground state. To that end, in this work, we examine the lowest singlet exited state S1 and lowest triplet excited state T1 for a total of 80 molecular systems, in comparison with their corresponding ground state S0. Computational details of these investigations are available in SI. The properties we consider include three aspects, conformational stability, bonding, and reactivity. We unveil unique behaviors of singlet and triplet excited states in conformational stability. We also discover bonding features and regioselectivity propensities for them. The strong correlations obtained between singlet and triplet excited state energy difference with quantities from OF-DFT, CDFT and ITA should provide us with new approaches to predict the propensity for singlet fission [32, 33], a photophysical process where one singlet exciton S1 is converted into two triple T1 excitons. This is vital to enhance the photoelectric conversion efficiency for photovoltaic devices in solar energy research and other areas [34].
2 Theoretical frameworks
Density-based reactivity theory in DFT consists of four frameworks [3], orbital-free DFT (OF-DFT), conceptual DFT (CDFT), density associated quantities (DAQ), and information-theoretic approach (ITA). ITA treats the molecular system as an information system with the electron density regarded as a continuous probability function normalized to the total number of electrons in the system, N [9, 10]. With this in mind, numerous quantities well defined in information theory can be borrowed. They are all density functionals with their expression in terms of the density and associated quantities is explicitly known. The first simple electron density functional is Shannon entropy [16],
with ρ(r) being the total electron density of the N-electron system, satisfying the following normalization condition,∫ρ(r)dr = N. The second one is the Fisher information [17],
with ∇ρ(r) as the density gradient. For homogeneous electron gas, where ∇ρ(r) vanishes, IF is zero. Integrating Eq. (2) by parts, we can obtain an equivalent expression for Fisher information in terms of the Laplacian of the electron density ∇2ρ. We define it as the alternative Fisher information [35],
Nevertheless, as proved earlier by one of us, due to the existence of the basic theorems in DFT and henceforth the redundance of information included in the density functionals, these ITA quantities are closely related through the following identity,
The fourth quantity in ITA is the Ghosh−Berkowitz−Parr(GBP) entropy [36, 37],
where k is the Boltzmann constant and t(r; ρ(r)) is the kinetic energy density, which is related to the total kinetic energy TS via∫t(r; ρ(r))dr = TS and tTF(r; ρ(r)) is the Thomas−Fermi kinetic energy density, tTF(r; ρ(r)) = cKρ5/3(r),with\({c}_K=\frac{3}{10}{\left(3{\pi}^2\right)}^{2/3}\), and \(c=\frac{5}{3}+\ln \frac{4{\pi c}_K}{3}.\) In ITA, we also have Rényi entropy of order n, where n ≥ 0 and n ≠ 1 defined as [38],
and the relative Rényi entropy of order n [39],
Where ρ0(r) is the reference state density satisfying the same normalization condition as ρ(r). Another important quantity in ITA is the relative Shannon entropy, also called Kullback−Leibler divergence, relative entropy, or information divergence [9, 40],
which is a gauge of the information gain or loss due to the formation of a molecular system from its composing ingredients. In Eq. (8), \({\rho}_0\left(\textbf{r}\right)\ {and}\ {\rho}_A^0\left(\textbf{r}\right)\)are the reference state density satisfying the same normalization condition as ρ(r) and ρA(r),\(\int \rho \left(\textbf{r}\right){d}\textbf{r}=\int {\rho}_0\left(\textbf{r}\right){d}\textbf{r}={\sum}_A\int {\rho}_A\left(\textbf{r}\right)d\textbf{r}={\sum}_A{\rho}_A^0\left(\textbf{r}\right)d\textbf{r}=N\). According to Nalewajski and Parr, minimizing the information gain subject to the condition that electron density normalization is held always true yields the stockholder partition of the electron density for atoms in molecules. The stockholder partition was first proposed by Hirshfeld, so we have [41,42,43],
Recent progress by us has shown that IG can be expanded by a Taylor series whose first-order term yields a vanished information gain [19],
where qA is the Hirshfeld charge. This suggests that the information before and after a system is formed should be conserved. We called this result the information conservation principle.
Another example of relative entropies is the relative Fisher information defined as [44, 45]
where \({}_F^ri\left(\boldsymbol r\right)\)is the relative Fisher information density. This is the conventional form of the relative Fisher information. The corresponding relative form for the alternative Fisher information is the following [35],
with \({}_F^r{i}^{\prime}\left(\textbf{r}\right)\) as the relative alternative Fisher information density. More recently, we have proved that for the information gain, IG, the following identity must be valid for atoms and molecules [40],
With,
In OF-DFT, where the concept of orbitals is not employed, we can deal with the total energy partition in the conventional form [12],
where TS, Vne, J, Vnn , and EXC stand for the noninteracting kinetic energy, nuclear–electron attraction, classical electron–electron Coulombic repulsion, nuclear–nuclear repulsion, and exchange–correlation energy density functionals, respectively. Since Vne, Vnn, and J are of the electrostatic nature, so we have,
In DFT, the contribution from the Pauli Exclusion Principle can be quantified by Pauli energy EP [46],
with
where EP, TS, and TW stand for the Pauli energy, total non-interacting kinetic energy, and Weizsäcker kinetic energy, respectively, and εP, t, and tW represent their corresponding local energy density. Pauli energy is the energetic contribution from the Pauli principle to kinetic energy [12, 47, 48]. There is also a contribution to potential energy, i.e., the exchange-correlation energy, but its magnitude is much smaller. We recently proposed a new scaled Pauli energy, which we call BNI (bonding and noncovalent interaction) index [15],
where we make use of the Weizsäcker kinetic energy itself as the reference to obtain the scaled Pauli energy. The reason that we call it BNI index is that this function can simultaneously identify both covalent and noncovalent interactions between atoms in molecules.
In CDFT, there exist a few well-established global reactivity descriptors, such as chemical potential μ [49], hardness η [5], and electrophilicity index ω, defined as [50],
where E is the total energy of the system, N is the total number of electrons, ν(r) is the external potential, and χ is the electronegativity defined by Iczkowski and Margrave. The hardness η, through Koopman′s theorem [51, 52],can be approximated as the energy gap between the lowest unoccupied molecular orbital (εLUMO) and the highest occupied molecular orbital (εHOMO),
For the first excited state [53], either S1 or T1 state,
With εSOMO is the energy of single occupies molecular orbital (SOMO).
To quantify regioselectivity and electrophilicity/nucleophilicity in CDFT, we use Fukui function [51]. It was defined as the differential change of the electron density ρ(r) induced by a change in the total number of electrons N or equivalently as the functional sensitivity of a system’s chemical potential μ to perturbations in the external potential v(r) [54, 55],
In the condensed-to-atom form of the Fukui functions, we have [56]
where \({q}_N^A\) is the charge on atom A with the entire molecule having a total of N electrons. Also, the local temperature Τ(r) of a molecule can be defined in terms of its kinetic energy density (KED) [36, 57, 58],
where τ(r), ρ(r), and κB are the KED, electron density, and Boltzmann constant, respectively. Additionally, we have previously shown that local temperature can also be used as a descriptor for electrophilic and nucleophilic attacks. For nucleophilic attack, we have [59]
and for electrophilic attack, it is
where ΤN, ΤN + 1, and ΤN − 1 are local temperatures for the system with N, N + 1, and N − 1 electrons, respectively, in the N electron geometry.
In this work, we will apply these density-based frameworks to investigate two excited states, S1 and T1, in comparison with the ground state, S0, for several molecular systems.
3 Computational details
All optimized structures and electronic wave functions were obtained from the Gaussian 16 package, version C1 [60], with tight SCF convergence and ultrafine integration grids. The molecules studied in this paper (Scheme 1) were optimized using the hybrid exchange-correlation energy density functional M06-2X [61] and Dunning's aug-cc-pvtz [62] basis set. The spin multiplicity of the first excited state of the atom is consistent with the experimental determination. The time-dependent density functional theory was used for the calculation of the first singlet excited state of the molecule. We performed benchmark tests of three states (S0, S1, T1) for two molecules with DFT M062X and Hartree-Fock methods and only qualitatively different results were observed, whose results are shown in SI (Fig. S0). All energetic components were obtained with Gaussian using the keyword IOP(5/33=1). The Multiwfn program, version 3.8 [63], was utilized to calculate BNI index, ITA quantities, Fukui functions, and local temperature with the checkpoint file from the Gaussian calculations as the input file. We obtained all contour surfaces with GaussView. Atomic units are used for all ITA quantities. For stability, the unit is kcal/mol.
4 Results and discussion
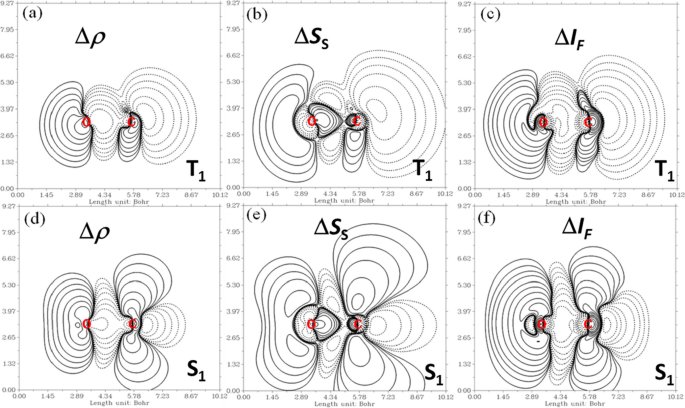
Figure 1, as an illustrative example, shows the difference map of the total electron density (Fig. 1a and d), Shannon entropy (Fig. 1b and e), and Fisher information (Fig. 1c and f) for carbon monoxide in the first excited singlet S1 and triplet T1 states with the ground state S0 value as the reference. As can be found in the Figure, for the density difference map in Fig. 1a for T1, the positive region (i.e., electron density accumulation) is mainly located on the terminal side of oxygen (on the left). This pattern is qualitatively the same for Shannon entropy in Fig. 1b and Fisher information (Fig. 1c), though quantitative differences among them are discernible. These details of quantitative differences are crucial when molecular properties are quantified by them. In S1, however, from the density difference map in Fig. 1d, we find that there are density accumulations on both carbon and oxygen atoms, just that for O, the positive regions are on the terminal, whereas for C, they are resided on the two sides of the C-O bond. Again, Shannon entropy (Fig. 1e) and Fisher information (Fig. 1f) yield qualitatively similar results, though, quantitatively, there are subtle differences among them. These results highlight that (i) the two lowest excited states can yield significantly different results from the ground state due to their vastly different density redistributions, and (ii) ITA quantities as simple density functionals can yield details of the heterogenous electron density distribution that are essential for the quantitative evaluation of physiochemical properties.
In Table 1, we list numerical results of six ITA quantities for 24 molecules (Scheme 1) in S1 state using their respective values in S0 state as the reference (i.e., in terms of S1-S0). Table 2 are the results for T1 state. Their S0 values are shown in SI (Fig. S2). Also included in SI are numerical results of a series of atoms (Fig. S1). The six ITA quantities in Tables 1 and 2 are the following 3 pairs: (i) Shannon entropy SS and its relative form, relative Shannon entropy IG (also called information gain or Kullback-Leibler divergence); (ii) Fisher information IF and relative Fisher information rIF; and (iii) alternative Fisher information I’F and relative alternative Fisher information rI’F [40, 64]. It is known that these quantities are intrinsically interrelated [35, 40]. In principle, Shannon entropy and Fisher information gauges homogeneity and heterogeneity of the electron density distribution, respectively. In this regard, it makes sense to believe that, given that in excited states the electron density becomes more diffused, Shannon entropy ought to increase and Fisher information to decrease. Nevertheless, given the ununiform patterns observed in Fig. 1, no monotonicity of these ITA quantities is expected. This is precisely what we can confirm for most cases in the two Tables. The only exception is Shannon entropy for T1 in Table 2, where ΔSS is always positive, at least for this set of 24 molecules. This result indicates that in comparison with the value in S0, Shannon entropy in the T1 state is indeed monotonically increased, suggesting that the electron density in T1 is more uniformly diffused than that in S1. We also considered six other ITA quantities, whose results are shown in Fig. S3 for states S0, Fig. S4 for S1, and Fig. S5 for T1 for the 24 molecules in Scheme 1.
Table 1 Numerical values of six ITA quantities in first singlet excited state (S1) for 24 organic molecules. The excited state value is expressed as the difference with its counterpart the ground state value (S1-S0)
| ΔSs | ΔIG | ΔIF | ΔrIF | ΔI’F | ΔrI’F | |
|---|---|---|---|---|---|---|
| acetaldehyde | 0.190 | 0.008 | 1.144 | -0.811 | 1.144 | -0.321 |
| acetic acid | 0.301 | 0.012 | 1.889 | -1.179 | 1.889 | -0.522 |
| acetone | 0.209 | 0.003 | 1.128 | -0.812 | 1.128 | -0.309 |
| benzaldehyde | 0.108 | 0.016 | 0.912 | -0.592 | 0.909 | -0.231 |
| biphenyl | 0.194 | -0.004 | 0.830 | -0.671 | 0.835 | -0.301 |
| bipyridine | -0.014 | -0.010 | -0.030 | -0.029 | -0.031 | -0.003 |
| cycloheptatriene | 0.073 | 0.005 | 0.328 | -0.374 | 0.326 | -0.076 |
| cyclopentene | 0.080 | -0.003 | -0.391 | 0.065 | -0.390 | 0.136 |
| cyclopropane | 0.266 | -0.007 | 1.335 | -0.758 | 1.336 | -0.361 |
| dimethyl ether | -0.062 | -0.002 | -0.596 | 0.185 | -0.597 | 0.236 |
| ethylamine | 0.104 | -0.011 | -1.653 | 0.339 | -1.653 | 0.684 |
| formamide | 0.304 | -0.001 | 2.751 | -1.371 | 2.752 | -0.943 |
| furan | 0.107 | -0.012 | -0.128 | -0.145 | -0.128 | 0.043 |
| isoindene | 0.194 | -0.015 | -0.013 | -0.399 | -0.010 | 0.086 |
| methyl formate | 0.301 | 0.012 | 1.889 | -1.180 | 1.889 | -0.522 |
| methylamine | 0.094 | -0.009 | -1.565 | 0.311 | -1.565 | 0.661 |
| pentalene | 0.281 | -0.014 | 0.164 | -0.616 | 0.164 | 0.073 |
| pyrazine | 0.060 | 0.005 | -0.047 | -0.295 | -0.045 | 0.116 |
| pyridazine | 0.003 | 0.006 | -0.548 | 0.147 | -0.549 | 0.223 |
| pyridine | 0.127 | 0.006 | 0.049 | -0.487 | 0.049 | 0.123 |
| pyrimidine | 0.105 | 0.017 | -0.323 | -0.357 | -0.324 | 0.301 |
| pyrrole | 0.138 | -0.009 | -0.224 | -0.190 | -0.223 | 0.137 |
| styrene | 0.199 | -0.006 | 0.577 | -0.643 | 0.575 | -0.146 |
| thiophene | 0.312 | -0.011 | 0.704 | -1.053 | 0.701 | 0.041 |
Table 2 Numerical values of six ITA quantities in the triplet excited state (T1) for 24 organic molecules. The excited state value is expressed as the difference with its counterpart the ground state value (T1-S0)
| ΔSs | ΔIG | ΔIF | ΔrIF | ΔI’F | ΔrI’F | |
|---|---|---|---|---|---|---|
| acetaldehyde | 0.402 | -0.049 | 0.486 | -1.870 | 0.484 | 0.536 |
| acetic acid | 0.451 | -0.030 | 1.911 | -1.957 | 1.911 | -0.129 |
| acetone | 0.437 | -0.053 | 0.831 | -1.670 | 0.830 | 0.222 |
| benzaldehyde | 0.407 | -0.056 | 0.023 | -1.752 | 0.019 | 0.671 |
| biphenyl | 0.226 | 0.000 | 0.629 | -0.885 | 0.633 | 0.112 |
| bipyridine | 0.181 | -0.004 | 0.978 | -1.191 | 0.978 | 0.119 |
| cycloheptatriene | 0.101 | -0.026 | -0.153 | -1.002 | -0.155 | 0.610 |
| cyclopentene | 0.233 | -0.034 | 0.148 | -1.362 | 0.148 | 0.666 |
| cyclopropane | 3.477 | 1.294 | 2.678 | 1.457 | 2.581 | -1.644 |
| dimethyl ether | 3.551 | 0.986 | 0.096 | 1.144 | 0.013 | -0.573 |
| ethylamine | 2.872 | 0.740 | -0.294 | 0.661 | -0.344 | -0.135 |
| formamide | 0.435 | -0.043 | 1.899 | -2.007 | 1.899 | -0.153 |
| furan | 0.094 | -0.003 | 1.563 | -1.695 | 1.562 | 0.246 |
| isoindene | 0.045 | -0.021 | 0.148 | -0.638 | 0.151 | 0.274 |
| methyl formate | 0.451 | -0.030 | 1.911 | -1.957 | 1.911 | -0.129 |
| methylamine | 3.004 | 0.757 | -0.604 | 0.689 | -0.660 | 0.040 |
| pentalene | 0.031 | -0.012 | 0.706 | -0.931 | 0.705 | 0.129 |
| pyrazine | 0.433 | -0.080 | -2.284 | -1.606 | -2.284 | 1.918 |
| pyridazine | 0.314 | -0.086 | -3.972 | -1.000 | -3.973 | 2.448 |
| pyridine | 0.400 | -0.048 | -0.558 | -1.681 | -0.559 | 1.103 |
| pyrimidine | 0.396 | -0.087 | -1.645 | -1.704 | -1.647 | 1.578 |
| pyrrole | 0.076 | 0.009 | 2.085 | -1.679 | 2.085 | -0.077 |
| styrene | 0.211 | -0.016 | 0.292 | -1.089 | 0.290 | 0.443 |
| thiophene | 0.076 | 0.004 | 1.367 | -1.583 | 1.363 | 0.183 |
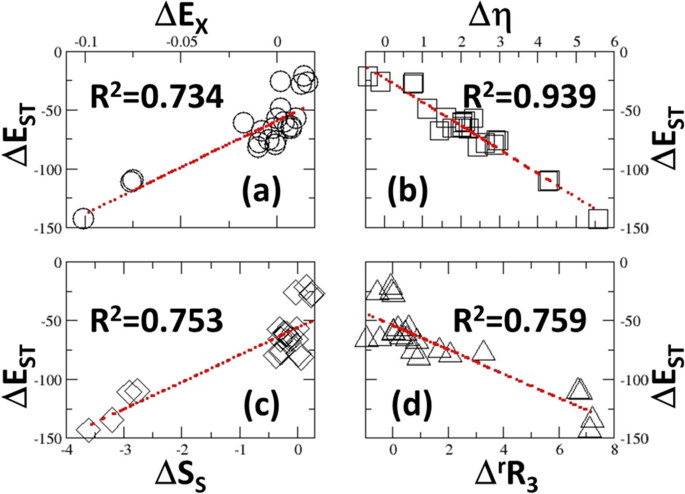
Shown in Fig. 2 are strong linear correlations of the total energy difference between the two excited state, ΔEST = E(S1) − E(T1), with four density-based electronic properties: (a) the exchange energy change ΔEX; (b) chemical hardness change Δη; (c) Shannon entropy change ΔSS; and (d) third-order relative Rényi entropy change ΔrR3 for 24 molecules in Scheme 1. This energy difference has been found to have huge implications in singlet fission in the literature to design better photovoltaic devices in solar energy applications [32,33,34]. From the Figure, we can see that exchange energy from OF-DFT (Fig. 2a) and hardness from CDFT (Fig. 2b) are decent descriptors of ΔEST. These two descriptors were recently reported by Wang and Bu. [34] Fig 2c and d are two new possible descriptors from ITA, Shannon entropy ΔSS and third-order relative Rényi entropy change ΔrR3 that we first discovered in this work. These descriptors could be combined to yield prediction models for the discovery of new singlet fission materials. Systematical studies are underway to utilize these strong correlations in designing better singlet fission sytems.
Strong linear correlations of the total energy difference between two excited states, S1 and T1, defined as ΔEST = E(S1) − E(T1) with four electronic properties: a the exchange energy change ΔEX; b the chemical hardness change Δη, (η are valued by Eq. 25 and 26); c Shannon entropy change ΔSS; and d third-order relative Rényi entropy change ΔrR3 between the two excited states S1 and T1 for 24 molecules (Scheme 1) in Tables 1 and 2
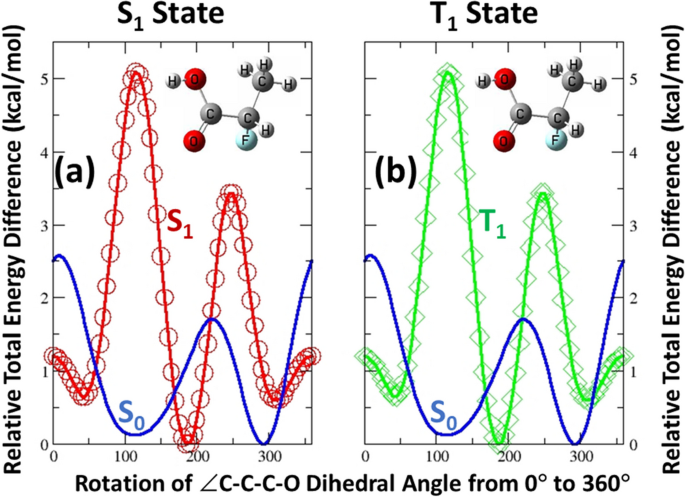
Now let us examine the conformational stability for the excited states. Taking acetic acid substituted by fluorine and methyl groups as an example, we rotated the flexible C-C bond through ∠Me-C-C-OH dihedral angle from 0° to 360° with the step size of 5° for three states, S0, S1, and T1, in which other structural parameters would be optimized accordingly.
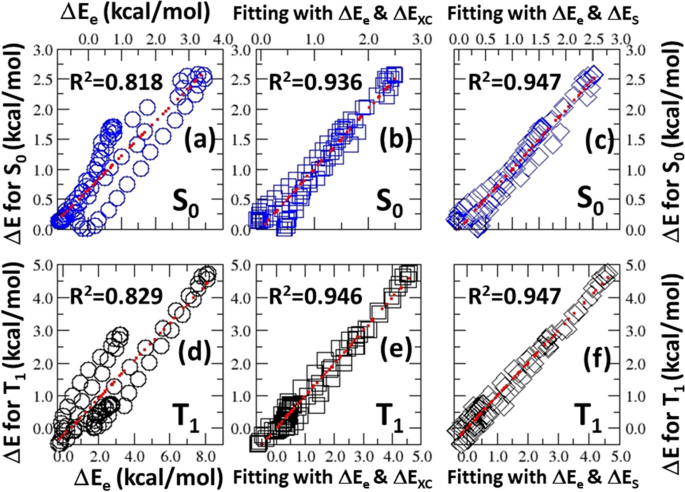
Figure 3 is the total energy profiles of these three states as a function of the C-C bond rotation angle with Fig. 3a for S1 and Fig. 3b for T1 and the blue curve in both figures representing the behavior of the ground state S0. We plotted the profiles using their lowest energy conformation as the reference. Two points are clear from the Figure. First, the energy profile of the two excited states is totally different from that of the ground state. Their lowest energy conformation, i.e., the zero-energy point in the plots, is also completely different from that of S0. Secondly, from the viewpoint of curve shapes, the profiles of S1 and T1 look quite similar, and their lowest energy conformations are also similar with the same dihedral angle. Does this mean that S1 and T1 behave the same from the energetics viewpoint? Not quite! Following our prior studies [47, 48, 65,66,67,68,69,70,71] on two schemes to perform the total energy partition, Fig. 4 shows the results for S0 and T1 states. For the ground state, same as our previous results [47, 48, 65,66,67,68,69,70,71], the electrostatic component ΔEe was found to be strongly correlated with ΔE (Fig. 4a). If ΔEe is fitted together with either the exchange-correlation component ΔEXC (Fig. 4b) or steric energy ΔES, markedly improved correlation with ΔE can be obtained, each with R2 > 0.93. For the triplet excited state T1, these same correlations were obtained, as shown in Fig. 4d-f. However, for the lowest singlet excited state S1, none of such strong correlations has ever been observed. These results elucidate that even though energy profiles of S1 and T1 appear quite similar in Fig. 3, they are intrinsically different, at least from the viewpoint of energetics. This intrinsic difference between the two excited states will generate significant differences in bonding, reactivity, and other properties.
Profiles of the relative total energy as a function of the ∠C-C-C-O dihedral angle of the acetic acid derivative, CHFMeCOOH, from 0° to 360° with the step size of 5° for (a) the first excited singlet state S1 and (b) the first excited triplet state T1 using the lowest total energy as the reference for each state. The blue curve is the same profile of the ground state S0
Strong correlations of the total energy difference ΔE for S0 and T1 states. No such strong correlations can be found for the S1 state. a-c are for S0 state and d-f are for T1 state. a & d Relationship with the electrostatic energy difference ΔEe; b & e Fitting with electrostatic energy difference ΔEe & exchange-correlation energy difference ΔEXC; and c & f Fitting with electrostatic energy difference ΔEe & steric energy difference ΔES
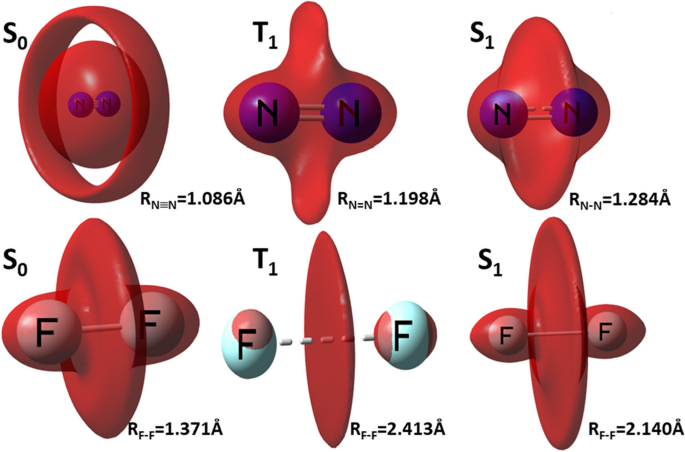
Applying density-based quantities to describe covalent and noncovalent interactions has been an integral part of the density-based reactivity theory [3]. Our earlier findings suggest that Pauli energy-based descriptors such as SCI (strong covalent interactions) [14] and BNI (bonding and nonbonding interaction) [15] indexes can do that job through the signature isosurface between the bonded atoms for each kind of interactions. These contour surfaces are unique to the same bonding or interaction type. For example, with BNI [15], for triple covalent bonds, the signature isosurface is like a disc or torus or hula hoop; for double covalent bonds, it is like two blades of a propeller pointing to opposite directions; for single covalent bonds, the signature shape is like a grinding wheel with the bar handle connected to the two bonded atoms; and for van der Waals interactions, it is a disjoint disk perpendicular to the two interacting atoms [15]. With this in mind, we examined the bonding characteristics for homogeneous diatomic molecules, N2 and F2, in three electronic states, S0, S1, and T1. Shown in Fig. 5 are the BNI signature isosurfaces for the two dimers in three states. Also shown in the Figure is the optimized bond length for each species. From the Figure, it is unambiguous that N2 in S0 is a triple covalent bond, in T1 it is double bond, but in S1 it becomes single covalent bond. For F2, the bond/interaction type for S0, T1 and S1 states is single covalent bond, van der Waals interaction, and single covalent bond, respectively. These results can be confirmed by the bond order analysis for these species. For example, using Laplacian bond order analysis, we obtained that the bond order of N2 in S0, T1, and S1 states is 3.261, 2.136, and 1.433, respectively, suggesting that they are triple, double, and single covalent bonds. These bond order results are good agreement with what we have obtained in Fig. 5.
The signature isosurface of BNI (Bonding and noncovalent interaction) index for N2 and F2 molecules in three electronic states, S0, T1, and S1. Also shown are the bond distance of these species in three different electronic states. The isovalue for N2 is 0.11 for S0; 0.65 for T1; and 0.43 for S1. For F2, the isovalue is 0.55 for S0; 1.10 for T1; and 0.40 for S1. Units in a.u
Next, we examine the reactivity property for excited states. For that purpose, at first, we consider regioselectivity for the electrophilic aromatic substitution reaction with ortho/para and meta directing groups. Earlier, our studies [21, 22] suggested that information gain from ITA and Hirshfeld charge as the first-order approximation of information gain can both be applied to determine regioselectivity for this reaction. Hirshfeld charge is relatively small in magnitude compared to other types of partial charges, but the subtle difference between Hirshfeld charges is a robust descriptor of electrophilicity, nucleophilicity, and regioselectivity propensities [21, 22]. Shown in Table 3 is the result of benzene derivatives with 15 different ortho/para directing groups, and in Table 4 is that with 15 meta-directing groups for all three states. In Table 3, for the ground state S0, Hirshfeld charge at ortho and para positions possesses the largest value, suggesting that they are the most likely locations to be substituted by an incoming electrophile, which is in excellent agreement with experimental evidence. For the triplet excited state T1, from Table 3, we can see that regioselectivity propensity of electrophilic substitutions is switched to the meta position, because the meta position has the largest negative charge in most cases. However, this switch of regioselectivity propensity is not always true. Among the 15 species we examined in this work, there are three exceptions, Ar-N(COCl)2, Ar- NH2Ar+, and Ar-OCONH2, indicating that ortho/para directing groups in ground state are often, but not always, changed to be meta-directing in T1 state. For S1, there is no apparent pattern observed in Table 3. For the meta-directing groups in S0, as shown in Table 4, we also discovered the same behavior of the switched regioselectivity propensity. In this case, S0 state favors the meta position for the electrophilic substitution, but in the T1 state the propensity is changed to ortho/para positions. This switch is not always the case either. In Table 4, we found Ar-PO2, Ar-PH2, and Ar-SiHO as exceptions, suggesting that meta directing groups in ground state are often, but not always, changed to be ortho/para-directing in T1 state. For S1 state in Table 4, we observed a similar pattern to T1, where in most cases, regioselectivity is switched to ortho/para positions, with only two exceptions. This result shows that for the meta-directing groups in the ground state, they often, but not always, become ortho/para directing groups in both S1 and T1 excited states.
Table 3 Hirshfeld charges at ortho/meta/para positions as a descriptor of regioselectivity for the aromatic electrophilic substitution reactions with 15 ortho/para directing groups in ground state S0, the lowest excited singlet state S1, and the lowest excited triplet state T1
| Group | S0 | T1 | S1 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ortho | Meta | Para | Ortho | Meta | Para | Ortho | Meta | Para | |
| -Ar | -0.043 | -0.042 | -0.044 | -0.037 | -0.049 | -0.030 | -0.038 | -0.045 | -0.035 |
| -O- | -0.121 | -0.091 | -0.142 | -0.128 | -0.172 | -0.066 | -0.070 | -0.117 | -0.100 |
| -Me | -0.049 | -0.044 | -0.049 | -0.092 | -0.102 | 0.054 | -0.053 | -0.052 | -0.026 |
| -CH-2 | -0.115 | -0.094 | -0.162 | -0.143 | -0.172 | -0.097 | -0.093 | -0.108 | -0.091 |
| -NH2 | -0.068 | -0.042 | -0.065 | -0.027 | -0.078 | -0.048 | -0.101 | -0.085 | -0.021 |
| -NH- | -0.115 | -0.091 | -0.153 | -0.127 | -0.169 | -0.081 | -0.067 | -0.094 | -0.091 |
| -NHMe | -0.071 | -0.045 | -0.068 | -0.022 | -0.081 | -0.052 | -0.098 | -0.095 | -0.032 |
| -NMe2 | -0.071 | -0.045 | -0.068 | -0.022 | -0.081 | -0.052 | -0.098 | -0.095 | -0.032 |
| -Et | -0.047 | -0.044 | -0.048 | -0.088 | -0.104 | 0.054 | -0.048 | -0.052 | -0.029 |
| -OCHO | -0.045 | -0.032 | -0.042 | -0.053 | -0.110 | 0.047 | -0.051 | -0.035 | -0.050 |
| -NHtBu | -0.069 | -0.045 | -0.068 | -0.050 | -0.062 | -0.034 | -0.118 | -0.085 | -0.026 |
| -tBu | -0.044 | -0.044 | -0.048 | -0.088 | -0.105 | 0.053 | -0.048 | -0.048 | -0.032 |
| -N(COCl)2 | -0.038 | -0.029 | -0.028 | -0.049 | -0.039 | 0.005 | -0.010 | -0.016 | 0.019 |
| -NH2Ar+ | -0.033 | -0.005 | -0.004 | -0.035 | -0.006 | -0.004 | -0.030 | -0.001 | -0.006 |
| -OCONH2 | -0.047 | -0.035 | -0.042 | -0.050 | -0.036 | -0.050 | -0.056 | -0.038 | -0.054 |
Table 4 Hirshfeld charges at ortho/meta/para positions as a descriptor of regioselectivity for the aromatic electrophilic substitution reactions with 15 meta directing groups in ground state S0, the lowest excited singlet state S1, and the lowest excited triplet state T1
| Group | S0 | T1 | S1 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ortho | Meta | Para | Ortho | Meta | Para | Ortho | Meta | Para | |
| -CHO | -0.031 | -0.038 | -0.026 | -0.048 | -0.044 | -0.051 | -0.048 | -0.042 | -0.051 |
| -COMe | -0.036 | -0.041 | -0.030 | -0.054 | -0.046 | -0.055 | -0.054 | -0.044 | -0.055 |
| -CONH2 | -0.041 | -0.042 | -0.033 | -0.053 | -0.046 | -0.055 | -0.058 | -0.047 | -0.058 |
| -COOtBu | -0.028 | -0.039 | -0.032 | -0.056 | -0.045 | -0.057 | -0.054 | -0.043 | -0.057 |
| -COOH | -0.030 | -0.038 | -0.028 | -0.044 | -0.033 | 0.004 | -0.049 | -0.042 | -0.054 |
| -COtBu | -0.028 | -0.038 | -0.032 | -0.055 | -0.045 | -0.057 | -0.054 | -0.044 | -0.058 |
| -COBr | -0.028 | -0.032 | -0.020 | -0.050 | -0.040 | -0.047 | -0.053 | -0.039 | -0.049 |
| -COCl | -0.029 | -0.033 | -0.021 | -0.045 | -0.022 | 0.013 | -0.050 | -0.038 | -0.047 |
| -NO2 | -0.028 | -0.029 | -0.022 | -0.044 | -0.031 | -0.036 | -0.040 | -0.029 | -0.035 |
| -NO | -0.029 | -0.032 | -0.022 | -0.045 | -0.034 | -0.041 | -0.053 | -0.034 | -0.050 |
| -PO | -0.031 | -0.038 | -0.021 | -0.039 | -0.034 | -0.036 | -0.039 | -0.033 | -0.037 |
| -SiH3 | -0.038 | -0.041 | -0.037 | -0.139 | 0.008 | -0.003 | -0.028 | -0.034 | -0.042 |
| -PO2 | -0.013 | -0.029 | -0.014 | -0.027 | -0.030 | -0.025 | -0.025 | -0.030 | -0.020 |
| -PH2 | -0.041 | -0.041 | -0.038 | -0.042 | -0.057 | -0.032 | -0.079 | -0.060 | -0.096 |
| -SiHO | -0.029 | -0.036 | -0.021 | -0.035 | -0.038 | -0.032 | -0.032 | -0.036 | -0.030 |
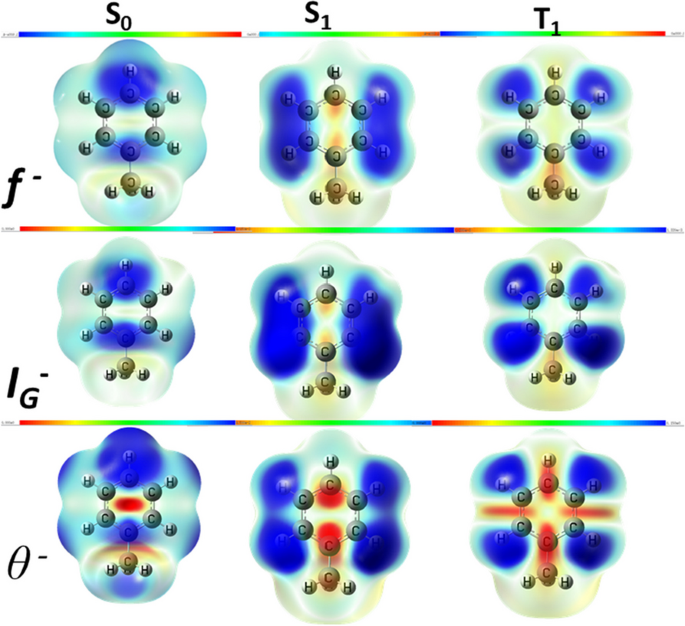
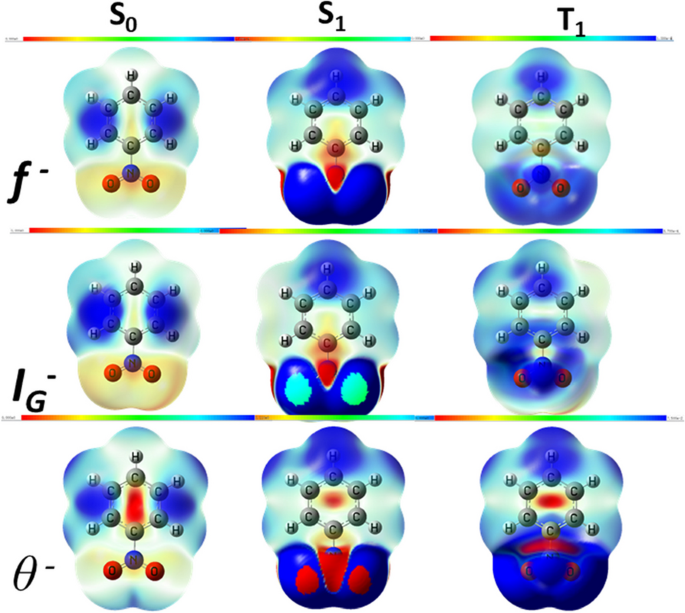
In density-bases reactivity frameworks, besides Hirshfeld charge, we can also leverage Fukui function [72] from CDFT, information gain from ITA [73], and local temperature [59] from OF-DFT, to determine regioselectivity propensity. Shown in Fig. 6 is the result of these additional approaches for toluene, which is known to be ortho/para directing in the ground state. In S1 and T1 states, it is changed to be a meta-directing group. In Fig. 7, the same was done for nitrobenzene, which is well known to be meta-directing in the ground S0 state. From the Figure, we can see that it is switched to be ortho/para directing in S1 and T1 states. These results, together with those from Hirshfeld charge in Tables 3 and 4, showcase that regioselectivity propensities in the excited states can be substantially different from the ground state. This is precisely the main reason why we can make use of these differences in photochemical processes to generate excited states and yield unexpected outcomes from them due to their reactivity differences for the purpose of synthesis and other transformations.
Employing three quantities, electrophilic Fukui function f -, information gain IG, and electrophilic local temperature θ -, as the regioselectivity descriptor for the electrophilic aromatic substitution of toluene in three electronic states, the ground state S0, first excited singlet state S1, first excited triplet state T1
Employing three quantities, electrophilic Fukui function f -, information gain IG, and electrophilic local temperature θ -, as the regioselectivity descriptor for the electrophilic aromatic substitution of nitrobenzene in three electronic states, the ground state S0, first excited singlet state S1, first excited triplet state T1
5 Conclusions
To summarize, in this work, we have examined the stability, bonding, and reactivity properties of the lowest singlet S1 and triplet T1 excited states, in comparison with their ground state S0, for a variety of molecular systems using the four density-based frameworks from density functional theory, including orbital-free DFT, conceptual DFT, information-theoretic approach, and direct use of density associated descriptors. Our results demonstrated that it is both feasible and productive to apply these density-based frameworks to appreciate physiochemical properties and propensities for excited states. Our present results also illustrated that excited state properties can be substantially different from ground state counterparts, thus highlighting the significance of the excited states in photochemical synthesis and reactions. This work, though in proof-of-concept fashion, is our first effort to apply density-based reactivity frameworks to formulate, quantify, and predict physiochemical properties for molecules in excited states. More studies are in progress to apply these four frameworks to real-world photochemical catalytic processes involved in solar energy such as photosynthesis, water oxidation and carbon dioxide reduction.