1 Introduction
1.1 Electromagnetic dipole response of nuclei
Electromagnetic responses of nuclei to the external field provides us with fundamental information on the property of nuclear matter and atomic nuclei that consist of nucleons, i.e., protons and neutrons [1]. An oscillating electric field with an angular frequency of \(10^{21-22}\) s\(^{-1}\) induced relative dipole oscillation between neutrons and protons in a nucleus. The oscillation is the Isovector Giant Dipole Resonance (GDR) and is a widely known example of nuclear collective motion. The existence of the GDR was predicted by Migdal [2] and was later observed in most nuclei except for very light nuclei such as \(^1\text {H}\) and \(^2\text {H}\).
Recently, a concentration of electric dipole (E1) excitation strength at around the neutron separation energy was experimental observed in neutron-rich nuclei. It is attracting attention in relation to the theoretical prediction of pygmy dipole resonance (PDR), which is described as the relative dipole oscillation between the excess neutrons and the isospin-saturated core. The static electric dipole polarizability (EDP) of a nuclei is obtained by integrating all the E1 excitation strengths, including the GDR and PDR, with the weight inversely proportional to the excitation energy. The EDP represents the size of the electric polarization in a static electric field. The information on the E1 nuclear response is crucial for determining the equation of states of neutron-rich matter governing the properties of neutron-rich nuclei and neutron stars.
Similarly, the spin-magnetic dipole (spin-M1) excitation of nuclei corresponds to the relative oscillation between the spin-up and spin-down nucleons. The oscillation mode is categorized as isoscalar (IS) when the neutrons and the protons are oscillating in phase and isovector (IV) out of phase. The spin-M1 excitation strength represents the magnetic response of the nuclei. Also, the amount of the spin alignment between a neutron and a proton in the ground state of a nucleus can be studied from the strength difference between the IS and IV spin-M1 excitations.
Those E1 and M1 excitations are relevant to photo-nuclear reactions. An absorption of a photon by a nucleus takes place primarily with the E1 excitation of the nucleus, and secondary by M1 excitation with more than one order of magnitude smaller than E1. Understanding the photo-nuclear reactions is essential for the astrophysical simulations of the photo-nuclear reactions in stars and in the intergalactic propagation of ultra-high-energy cosmic rays (UHECRs), as well as for various applications such as the design of radiation shielding, non-destructive inspection by photo-activation analysis, production of medical radioisotopes by photo-nuclear reactions, and biological effect under irradiation of gamma-rays [3, 4]. The inverse-process, photo-emission from giant resonances, is applicable for astrophysical neutrino detection with a neutral-current interaction.
Inelastic scattering cross sections of protons at the intermediate energy (300–400 MeV) and at a scattering angle close to zero degrees are primarily sensitive to the electric dipole excitation strengths of the target nuclei via virtual photon-exchange through Coulomb interaction and to the spin-magnetic dipole excitation strengths through nuclear interaction. This article highlights the study of electromagnetic dipole responses of nuclei achieved by proton scattering experiments at very forward angles performed at the Research Center for Nuclear Physics, Osaka University, employing the high-resolution magnetic spectrometer Grand Raiden.
This article is organized as follows. The nuclear matrix elements for each of electric dipole and magnetic dipole responses are formulated in the remaining part of Section 1. The experimental methods are described in Section 2. The electric dipole polarizability and the symmetry energy term of the nuclear equation of state are discussed in Section 3. A studies on the PDR is shown in Section 4. A study on the magnetic dipole excitation in self-conjugate nuclei is described in Section 5. Gamma decay coincidence measurement of PDR, gamma emission from giant resonances, and photo-nuclear reaction of light nuclei are introduced in Sections 6, 7, and 8, respectively. The article is summarized in Section 9.
1.2 Nuclear matrix elements
1.2.1 Electric dipole response
The E1 reduced transition probability B(E1) for an atomic nucleus is written as
where \(\left<f\Vert \mathcal {M}(E1)\Vert i\right>\) is the relevant E1 reduced transition matrix element for the initial state state i and the final state f, and \(J_{i(f)}\) is the spin of the initial (final) state. In this article, the initial state i is always the ground state. The E1 operator \(\mathcal {M}(E1)\) is defined, after the removal of the center-of-mass motion, as
The subscript p (n) stands for protons (neutrons), and the sum is taken for all the protons (neutrons). A proton and a neutron have an effective charge of \(e\frac{N}{A}\) and \(-e\frac{Z}{A}\), respectively.
The photo-absorption cross section by the E1 transition is related to the E1 reduced transition probability as
where \(\omega\) is the photon energy.
The energy-weighted sum-rule of the E1 transition, often called Thomas-Reiche-Kuhn (TRK) sum-rule, is expressed by the following equation [5]
or
The TRK sum rule is derived under the assumption that the potential energy of the nucleons is determined only by the position of the nucleons neglecting, e.g., exchange terms and the momentum dependence of the nuclear force.
1.2.2 Magnetic dipole response
The M1 reduced transition probability B(M1) caused by the electromagnetic interaction is written as
where \(J_{i(f)}\), \(T_{i(f)}\), and \(T_{zi(f)}\) are the spin, isospin nature, and the z-component of the isospin of the initial (final) state, respectively. The M1 operator \(\boldsymbol{\mu }\) is defined as [6]
where \(\mu _N\) is the nuclear magneton, \(\boldsymbol{l}_j(\boldsymbol{s}_j=\frac{1}{2}\boldsymbol{\sigma }_j)\) is the orbital (spin) angular momentum operator of the jth nucleon. The orbital gyromagnetic factor (g factor) \(g_l^{\pi (\nu )}\) is unity (zero) for a proton (neutron). The spin g factor \(g_s^{\pi (\nu )}\) is 5.586 (−3.826) for a proton (neutron). The isoscalar (IS) and isovector (IV) g-factors are the linear combination of the proton and neutron g-factors as \(g_{l(s)}^{\text {IS}}=\frac{1}{2}(g_{l(s)}^\pi +g_{l(s)}^\nu )\) and \(g_{l(s)}^{\text {IV}}=\frac{1}{2}(g_{l(s)}^\pi -g_{l(s)}^\nu )\).
Proton scattering is only sensitive to the spin part of the M1 transition matrix element through the nuclear interaction.
for the IS and
for the IV excitations. Here, \(C_{M1}\) denotes the isospin Clebsch-Gordan coefficient
The corresponding IS and IV nuclear matrix elements are denoted as
2 Experimental methods
2.1 Traditional methods
For the electric dipole excitation of nuclei, photon-induced reactions were used as a standard method of experimental studies. An intense real-photon beam with a continuous energy spectrum was produced through the Bremsstrahlung process by irradiating an electron beam to a radiator target with a high atomic number. The target nuclei absorbed a photon whose energy matched the energy of an excited state. The photo-absorption was observed either by detecting an emitted particle or a gamma-ray from the excited state or by detecting the characteristic gamma-rays from the daughter unstable nuclei in the activation analysis method. In these measurements, precise knowledge of the photon spectrum was required since the excitation energy dependence of the photo-absorption cross sections was extracted from the difference between two measurements with different incident electron energies.
Below the neutron separation energy, gamma rays emitted through the direct decay to the ground state were usually detected. The process was called nuclear resonance fluorescence (NRF). Above the neutron separation energy, the number of emitted neutrons was counted after thermalization by the surrounding material containing hydrogen. Since the neutron energy was not detected, the realization of a flat neutron detection efficiency against the neutron energy was essential for a reliable measurement [4, 7].
Alternatively, the photo-neutron cross sections in the GDR energy region were extensively measured [8] in 1970s to 1980s with an experimental method called positron annihilation in flight. In the method, quasi-monoenergetic gamma rays, with a typical width of \(~\sim\)3%, were produced by positron-electron annihilation during the flight of a positron beam in a gas target. The background contribution caused through Bremsstrahlung was simulated with an electron beam at the same energy and was subtracted from the positron beam data. A deconvolution analysis using a profile of the quasi-monoenergetic beam was required. A significant systematic difference between the data at Livermore and Saclay was reported. The data at New SUBARU [9] indicated that the one (two) neutron emission data at Livermore (Saclay) were more consistent with their data [4].
Later, laser Compton scattering (LCS) gamma-ray beams were developed at AIST [10], HI\(\gamma\)S [11], and New SUBARU. The energy was tunable by changing the circulated electron beam energy. The gamma rays produced by the Compton scattering at a scattering angle of 180\(^\circ\) were collimated to produce quasi-monoenergetic gamma rays with a typical width of 1–2% [12] in FWHM. Another advantage of using the LCS gamma-rays was the availability of high photon-beam polarization originating from the polarization of the laser beam. The polarized photon beam was useful to identify the parity of an excited state, e.g., the separation of the E1 and M1 transitions, from the azimuthal distribution of the decay gamma rays. However, the gamma-ray intensity was lower than a Bremsstrahlung beam and was \(10^6\) photons/sec at New SUBARU and \(10^7\) at HI\(\gamma\)S. Thus, the application was limited for targets with natural isotopic abundance or for the cases where grams of isotopically enriched target could be prepared.
2.2 Proton scattering method
A new method was developed in the end of 2000s. It utilized virtual-photon excitation of the target nucleus with a relativistic proton scattering at very forward angles. The experimental technique was developed at the Research Center for Nuclear Physics, Osaka University, using proton beams at 295 and 392 MeV [13]. The essential point was the realization of the detection of inelastic proton scattering at very forward angles, including zero degrees. At zero degrees, the proton inelastic scattering cross sections were dominated by Coulomb excitation of target nuclei through a virtual photon exchange. Magnetic dipole excitation mediated by nuclear interaction also occurred with cross sections smaller than electric dipole excitation. Those two components and the contribution from other multi-polarities were decomposed (multipole decomposition analysis) by fitting the angular distribution of the cross sections with a sum of the theoretical angular distribution of each multi-polarity [14] The spin-flip and spin-non-flip components of the cross sections were decomposed by polarization transfer analysis (PTA) using a polarized proton beam and measuring the polarization of the scattered protons at RCNP, to experimentally assure the MDA results [14,15,16].
The experimental technique is described in Section 2.3. Here, we list the advantages of the proton scattering method in comparison to the other historical methods: (1) The excitation cross sections were measured by detecting only the scattered protons, corresponding to an inclusive measurement that was relevant to the full photo-absorption cross section containing all the decay channels. (2) A broad excitation energy region, 5–22 (7–32) MeV for a proton beam at 295 (392) MeV, was covered in a single measurement. The scattered proton detection efficiency was high (typically 80–90% due to the high track reconstruction efficiency of wire chambers) and was almost flat over the covered excitation energy region. Except for very light nuclei, the measurable excitation energy fully covered the GDR. It also covered the neutron separation energy region where the PDR strength was predicted to be concentrated. (3) Good excitation-energy resolution of 20–30 keV was achievable by applying the dispersion matching technique. (4) The cross section was large compared to the case of electron scattering. The measurement was possible with isotopically enriched targets with an amount of 10 mg or even less. (5) Polarization transfer observables could be measured for, e.g., separation of E1 and M1. (6) Absolute photo-absorption cross sections were extracted from the measured proton scattering cross section with the help of the reaction theory assuming the Coulomb excitation mechanism. (7) By measuring coincidence with decaying charged particles or de-excitation gamma rays, the branching ratio of each excited state was obtained.
However, one should consider the following points. (1) The excitation by proton scattering was not purely electromagnetic, even at zero degrees. The nuclear interaction contribution needed to be considered by, e.g., Eikonal approximation calculation of Coulomb excitation or Distorted Wave Born Approximation (DWBA) calculations. (2) Multipole decomposition analysis (MDA) was required for separating each multipole component. (3) A stable beam without accompanying background particles (beam halo) was indispensable to measure the inelastic scattering at zero degrees. (4) To further extend the excitation energy region was not possible in the zero-degree measurement since the magnetic field of the spectrometer was fixed for transporting the beam to the beam dump.
2.3 Proton inelastic scattering measurement at very forward angles
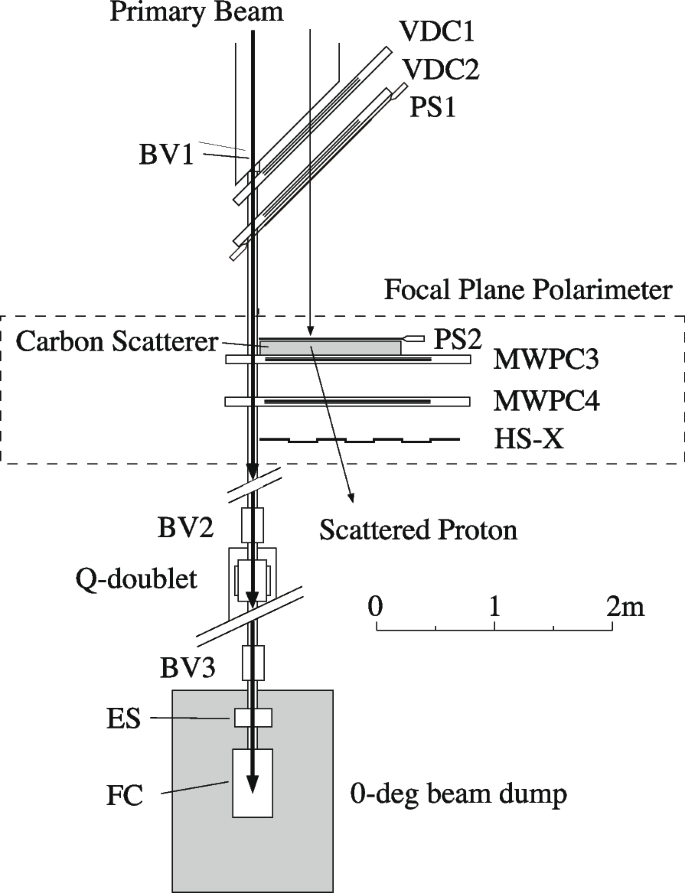
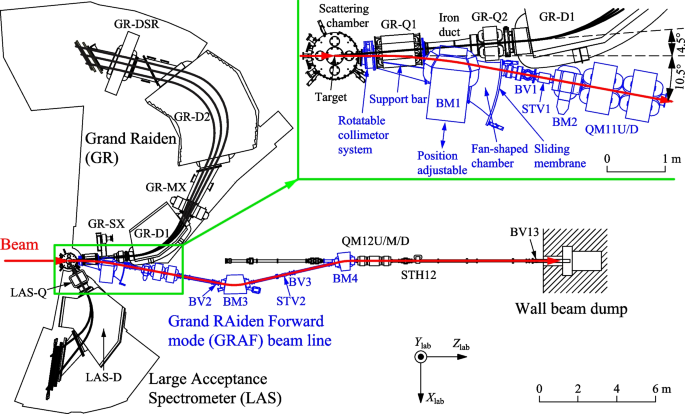
The experimental setup for the zero-degree measurement is shown in Fig. 1 [13, 17]. A proton beam was accelerated to 295 MeV or 392 MeV by the AVF (azimuthally varying field) and the RING cyclotrons in a cascade, transported through a high-resolution WS (West-South) beamline [18]. It bombarded a target placed in the scattering chamber. A typical beam current was 1–2 nA. The target thickness was 5 mg/cm\(^2\) or less, except for light nuclei like carbon, for reducing the background particles caused by the angular spread of the beam in the target. The unreacted beam that passed through the target is transported inside the high-resolution magnetic spectrometer Grand Raiden [19] and was stopped in a Faraday cup (FC) placed in the zero-degree beam dump shielded by concrete as shown in Fig. 2.
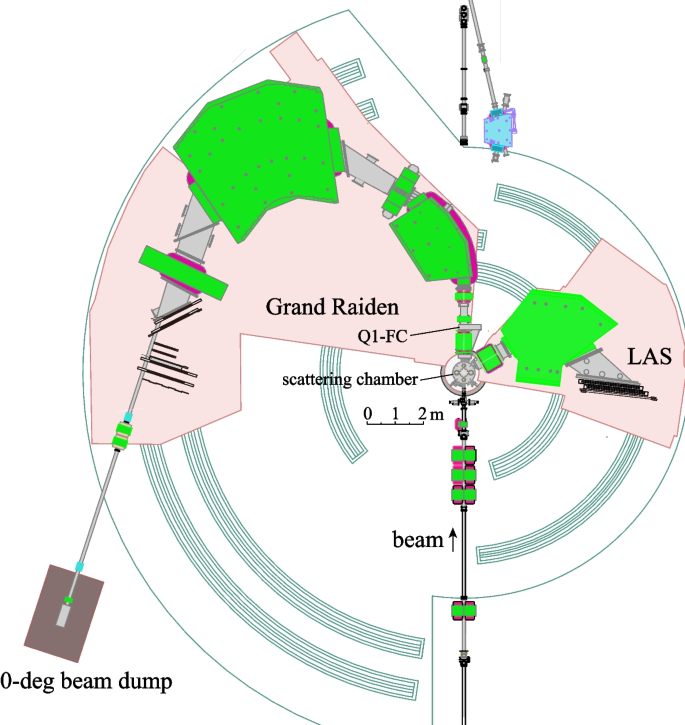
Grand Raiden spectrometer in the zero-degree inelastic scattering mode [17]. After passing through the target in the scattering chamber, the primary beam was transported in the Grand Raiden spectrometer and was stopped in the zero-degree beam dump
Two multiwire drift chambers of vertical drift type (VDCs), a plastic scintillator (PS1), and a focal plane polarimeter (FPP) are placed at the focal plane of the Grand Raiden spectrometer [17]. The FPP consisted of a plastic scintillator (PS2), carbon scatterer, two multiwire proportional chambers (MWPCs), and a plastic scintillator horoscope (HS-X)
Inelastically scattered protons were bent more than the unreacted beam in the spectrometer and were detected at the focal plane by two multi-wire drift chambers and plastic scintillators (Fig. 2). The distance between the unreacted beam and the sensitive area of the multiwire drift chambers of vertical drift type (VDCs) was 20 cm. A focal plane polarimeter (FPP), consisting of two multi-wire proportional chambers and a plastic scintillator horoscope, was placed for measuring the proton beam polarization by the second scattering in a carbon block. Since the magnetic field of the spectrometer was adjusted for transporting the unreacted beam to the beam dump, the covered excitation energy range was accordingly fixed.
A high-quality beam without a beam halo was essential to realize the zero-degree inelastic scattering measurement. A tiny amount of halo produced many background protons that dominated the signal in the focal plane detectors. The high-quality beam was achieved by careful operation and fine-tuning of the accelerators as described in Ref. [13].
In the measurement with Grand Raiden at an angle larger than zero degrees, the beam duct between the zero-degree beam dump and a quadrupole doublet was removed (see Fig. 1). The spectrometer could be set at different angle, e.g., 2.5, 4.5, or 6°. The beam was stopped at the Q1-FC placed behind the first quadrupole magnet of the spectrometer. For the angle larger than 6 degrees, the beam was stopped at another Faraday Cup placed in the scattering chamber (SC-FC). With these operation modes, the proton scattering angle was continuously covered from 0 to 70°. The beam stopped at SC-FC or Q1-FC produced a lot of background radiations, including neutrons and gamma rays. When decay particle or gamma detectors were set around the target position, the beam were needed to be stopped at the zero-degree beam dump in the zero-degree transmission mode or at a wall beam dump by using the GRAF beam line as described in Section 2.5.
2.4 DAQ system
A fast data acquisition (DAQ) system was essential for realizing the zero-degree inelastic scattering measurement since many background signals were produced even with a best-quality halo-free beam. The first DAQ system was in operation in 1994 based on VME data-bus and LeCroy digital converters employing ECL data transfer. The typical DAQ rate was 2–3 kHz. The TDCs for the wire chambers were discontinuously upgraded from LeCroy 4299 to LeCary 3377 in 1997, and later CAEN V1190A in 2011. The typical DAQ rate was 5 kHz. The DAQ system was upgraded to a system capable of a DAQ rate of 40–50 kHz in 2023. An even faster system is under development (S. Ota, N. Kobayashi. Private communication; unpublished).
2.5 Grand RAiden Forward (GRAF) mode beamline
Grand RAiden Forward (GRAF) mode beamline [20] (Fig. 3) was constructed in 2014 to be coupled with the Grand Raiden spectrometer at RCNP. The construction aimed to measure inelastically scattered particles by the spectrometer, and decay particles or gamma rays, in coincidence, by the detectors surrounding the target. The reaction was denoted by \((x,x'c)\), where x was the incident beam particle, and c was the decay particle or the de-excitation \(\gamma\) ray. The x particle was used for probing the response of the target nucleus, and the c particle acted as a messenger from the excited state. In this measurement, background radiations needed to be small enough at the decay detectors. Therefore, the primary beam was stopped far from the targets. The GRAF beamline guided the unreacted beam into a well-shielded wall beam dump located 25 m downstream from the target.
The GRAF beamline consisted of a GRAF scattering chamber, a rotatable collimetor system, a GR-Q1 vacuum chamber, a pure-iron vacuum chamber between the quadrupole magnet GR-Q1 and the sextupole magnet GR-SX, a fan-shaped vacuum chamber, dipole magnets, quadrupole magnets, steering magnets, and beam viewers. The pure-iron was used for shielding the magnetic field of the first bending magnet (BM1) of the GRAF beam line. A characteristic point of the beamline was using the horizontal bending power of a quadrupole magnet GR-Q1 for the off-axis beam to be deflected away from the central orbit of the GR spectrometer. Then, the beam was guided by bending magnets BM1 and BM2 so that its orbit was centered on the axis of the quadrupole magnets of the GRAF beamline. For each angle of the Grand Raiden spectrometer, the BM1 horizontal position was adjusted since the deflection power of GR-Q1 changes. In the GRAF mode, the Grand Raiden spectrometer could be placed at \(\theta _s = 4.5 - 19.0^{\circ }\) continuously except for \(\theta _s = 11.5 - 12.5^{\circ }\) where the unreacted beam hit a rod in the fan-shaped vacuum chamber for supporting the atmospheric pressure.
2.6 Gamma-coincidence measurements
Two types of experiments were performed employing a clover germanium detector array CAGRA (Clover Array Gamma-ray Spectrometer at RCNP/RIBF for Advanced Research) (E. Ideguchi, M.P. Carpenter, et al.: Germanium Clover detector array, CAGRA, in preparation) and large volume LaBr\(_3\):Ce detector array SC\(\gamma\)LLA (Supporting Construction for \(\gamma\)-ray-detecting Large LaBr3 Array) [21,22,23] coupled with the Grand Raiden spectrometer.
Campaign experiments using CAGRA and Grand Raiden spectrometer (CAGRA+GR setup) were performed by the CAGRA collaboration. The beam time was held from October to December 2016, allocated for 45 days of the beam time. One of the result is shown in Section 6.
SC\(\gamma\)LLA is a scintillation \(\gamma\)-ray detector array, which consisted of eight larger volume LaBr\(_3\):Ce detectors with a \(3.5''\phi \times 8''L\) cylindrical shape. Four detectors were located at 90\(^{\circ }\) and the other four at 135\(^{\circ }\). The distance between the target and the surface of the detector was adjustable for rate optimization and was set at the minimum distance of 137 (135) mm for 90 (135) \(^{\circ }\) detectors in a performed experiment. The target chamber was made from aluminum to reduce the attenuation of the \(\gamma\) rays. The target ladder was tiled by 22.5\(^{\circ }\) from the perpendicular direction of the beam. The solid angle coverage of the array was around \(20\%\) of \(4\pi\).
A measurement of the \(^{90}{\text {Zr}}(p,p'\gamma )\) reaction at \(\theta _s = 0^\circ\) and at \(E_p=392\) MeV was performed in July 2016 with the GR+SC\(\gamma\)LLA setup [21]. The maximum intensity of the beam was limited by the count rates of the detectors. For instance, the rate of a single crystal was around 150 kHz with a beam intensity of 2 nA on a \(^{90}\)Zr target with a thickness of 20.0 mg/cm\(^2\), when the beam was stopped at the \(0^\circ\) dump. On the other hand, when the beam was stopped at a Faraday Cup located 2 m downstream from the target, the count rate was around 200 kHz with a 0.2-nA beam with the same target. Usually, the scintillation detectors should have been operated with a count rate of less than around 200 kHz to keep the resolution and gain stability.
3 Electric dipole polarizability and the symmetry energy
As explained in Section 2.2, one of the strongest points of the proton scattering method is that the distribution of the full E1 reduced transition probability, B(E1), can be studied in a single-shot measurement from below the neutron separation energy up to above the higher energy tail of the GDR. Extraction of the sum rule value of the B(E1) distribution fully exploited the feature. The B(E1) distribution was determined over the excitation range from 5 to 19–22 MeV for \(^{208}{\text {Pb}}\) [14, 24], \(^{120}{\text {Sn}}\) [15, 25], \(^{96}{\text {Mo}}\) [16] by both the MDA and PTA and for \(^{90}{\text {Zr}}\) [26], \(^{48}{\text {Ca}}\) [27], \(^{112,116,120,124}{\text {Sn}}\) [28, 29] by MDA.
The E1 polarizability, \(\alpha _D\), was determined by applying the following E1 sum rule with the weight inversely proportional to the excitation energy, generally called the dielectric sum rule.
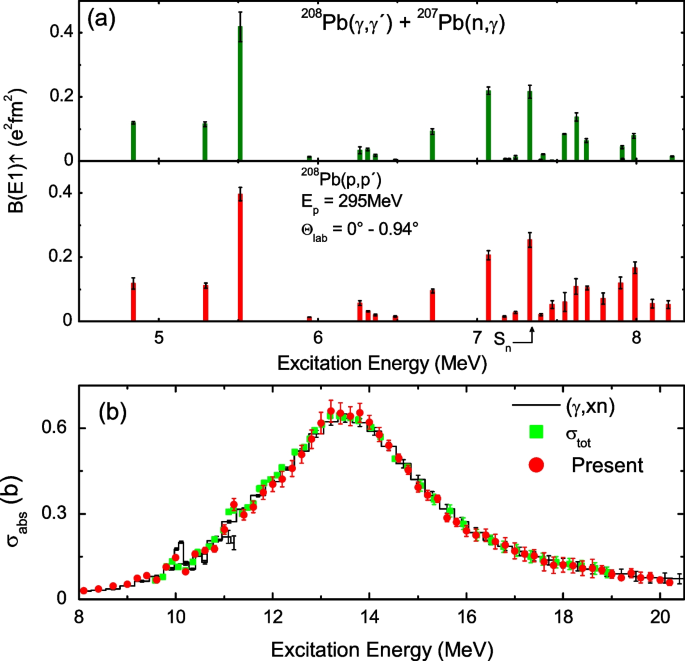
The B(E1) distribution in \(^{208}{\text {Pb}}\) is shown in Fig. 4. The data from the proton scattering experiment covered an excitation energy range of 5–19 MeV. The deduced E1 polarizability of \(^{208}{\text {Pb}}\) was \(20.1\pm 0.6\) fm\(^3\) [14], after adding 6% of the strength located above 19 MeV and below the pion mass taken from \((\gamma ,{\text {abs}})\) experiment data at Mainz [30]. The B(E1) polarizability of \(^{120}{\text {Sn}}\) was similarly determined to \(8.93\pm 0.36\) fm\(^3\) [15].
a The E1 reduced transition probability B(E1) of the low-lying discrete states in \(^{208}{\text {Pb}}\) measured by the \(^{208}{\text {Pb}}(\gamma ,\gamma ')\) and \((\gamma ,n)\) experiments [31,32,33,34] (upper panel) and by the \((p,p')\) experiment [14] (lower panel). b The photo-absorption cross section \(\sigma _{\text {abs}}\) in the GDR region. The red circles are from the \((p,p')\) experiment, the black line from \((\gamma ,xn)\) [35], and green squares from \((\gamma ,{\text {abs}})\) [30]
The E1 polarizability of those heavy spherical nuclei, in particular the \(^{208}{\text {Pb}}\) nucleus, was expected to be strongly correlated with the symmetry energy parameters of the nuclear equation of state. It was supported by relativistic and non-relativistic random phase approximation (RPA) calculations with the energy density functional (EDF) approach [36, 37].
The symmetry energy term, \(S(\rho ,\delta )\), of the nuclear equation of state is essentially the difference of the chemical potential between a neutron and a proton, i.e., the amount of the energy increase when replacing a proton by a neutron, in an infinitely large homogeneous nuclear matter. The nucleon number density of \(\rho\) and the asymmetry parameter \(\delta\) are defined as
where \(\rho _n\) (\(\rho _p\)) denotes the neutron (proton) number density. The symmetry energy is often expressed with the parameters J, L, and \(K_{\text {sym}}\) and the nucleon number density at the saturation density \(\rho _0\) (\(\sim 0.16\,{\text {fm}}^{-3}\)) as [38, 39]
The symmetry energy is extensively discussed in connection with, for example, the neutron-skin thickness of neutron-rich nuclei, the heavy-ion collision process, neutron star properties as the mass-radius relation, the nature of the gravitational wave produced by neutron-star mergers, supernova dynamics, and the cooling process of a proto-neutron star [40]. Therefore, the determination of the symmetry energy parameters is of crucial importance in nuclear physics and nuclear astrophysics research.
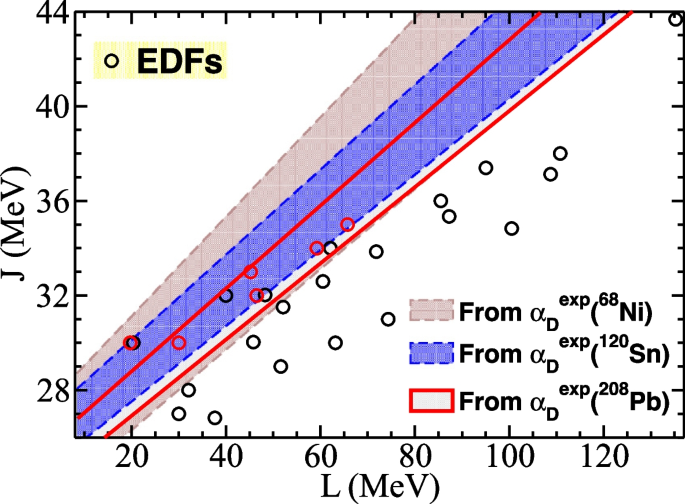
Constraint bands on the symmetry energy parameters J and L were deduced [37] by comparison with the predictions using various parameter sets of Skyrm and covariant EDFs. They are shown in Fig. 5 for each of the \(\alpha _D\) data on \(^{208}{\text {Pb}}\) and \(^{120}{\text {Sn}}\) measured at RCNP and the data on unstable \(^{68}{\text {Ni}}\) measured at GSI. The constraint bands from the three \(\alpha _D\) data consistently overlap with each other. Other experimental data, e.g., the neutron skin thickness of \(^{208}{\text {Pb}}\), would be required to further constrain the allowed region.
Constraint bands of the symmetry energy parameters J and L obtained from each of the E1 polarizabilities (\(\alpha _D\)) of \(^{208}{\text {Pb}}\) [14] and \(^{120}{\text {Sn}}\) [15] by \((p,p')\) at \(^{68}{\text {Ni}}\) [41] by Coulomb excitation in inverse kinematics at GSI. The circles are model predictions for various sets of energy density functional (EDF) parameters. Adapted from [37]
Parity violating electron scattering experiment at J-LAB (PREX [42, 43] and PREX-II [44, 45]) aimed at determining the neutron skin thickness of \(^{208}{\text {Pb}}\) and L from the data by using a model-independent analysis of the reaction through the weak-interaction. Although the present statistical uncertainty is still large to draw a definitive conclusion, the extracted neutron skin thickness implies a larger L value of \(106\pm 37\) MeV than expected from the E1 polarizability data [46].
Recent analysis of the gravitational wave signal GW170817 [47] from a neutron star merger indicated a tidal deformation of the neutron stars [48, 49] of the neutron stars and quiescent low-mass X-ray binaries [50, 51] gave constraints on neutron-star properties and the symmetry energy parameters.
4 Pygmy dipole resonance
A concentration of E1 strength at around the neutron separation energy \(S_n\) was reported for many nuclei with more neutrons than protons. The strength concentration is called a low-lying E1 mode (LED). The LED is regarded to be relevant to the concept of PDR, which is the dipole oscillation between the excess neutrons and the isospin-saturated core [1, 52,53,54].
The strength concentrations were observed by nuclear resonance fluorescence (NRF) experiments measured by detecting individual excited states. Since the B(E1) strength multiplied by the branching ratio of the ground-state gamma-decay was measured by the conventional NRF method, a 100% branching ratio, \(\Gamma _{\gamma _0}\)=1, was implicitly assumed in the discussion of the PDR strength.
Later, in several cases, the full B(E1) strength applying a correction using theoretically predicted \(\Gamma _{\gamma _0}\) with the statistical decay calculation was discussed.
The PDR strength distributes at around the neutron decay threshold. The NRF measurement is insensitive to the full strength above \(S_n\) since the neutron decay channel dominates the decay once it is opened. Even below \(S_n\), cascade gamma-decay channels may have sizable branching ratios depending on the nuclear level density. In addition, the proton decay channel opens in the same energy region for nuclei close to the stability line. Thus, the experimental determination of the ground state gamma-decay branching ratio, or the full B(E1) strength, is necessary to access the realistic PDR strength distribution.
One of the strong points of the present study is that proton inelastic scattering measurement is sensitive to the full B(E1) strength containing all the decay channels and not to the partial B(E1) strength of each decay channel. In addition, the deduced B(E1) by MDA contains the contribution from the collection of small transition strengths, while the conventional NRF is applicable only for prominent peak strengths.
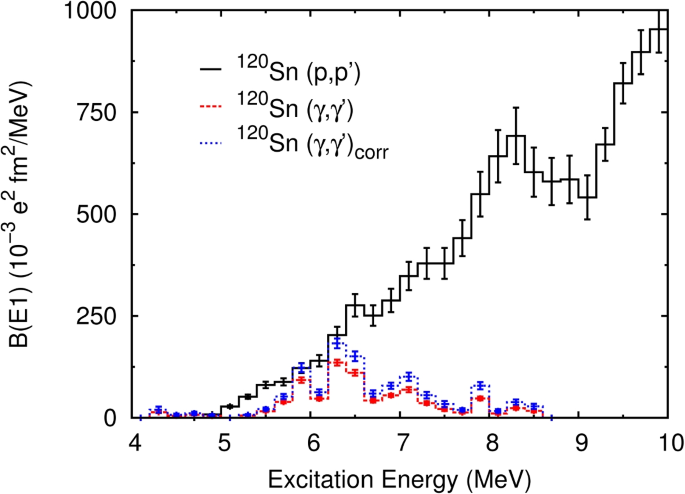
The PDR strength distribution was studied by the proton inelastic scattering measurement for\(^{208}{\text {Pb}}\) [24], \(^{90}{\text {Zr}}\) [26], and \(^{120}{\text {Sn}}\) [25] nuclei. As shown in Fig. 6, the strength observed by the conventional NRF measurement in \(^{120}{\text {Sn}}\) was remarkably smaller than the proton scattering data above 6.5 MeV. In this case, correction by the statistical decay calculation did not improve the extraction of the full strength. It is evident that the full distribution of the PDR strength much better obtained by the proton scattering method.
The B(E1) strength distribution in \(^{120}{\text {Sn}}\) at around the neutron separation energy of 9.1 MeV. The black line is from the \((p,p')\) experiment [25], the red dashed line from an NRF measurement [55], and the blue dotted line from the NRF with correction of the ground state decay branching ratio by a statistical model calculation. The figure was taken from Ref. [25]
We note that there were a few technical developments for extracting the full B(E1) strength around the neutron separation energy from NRF measurements: extraction of the unresolved strengths [56] and inelastic cross sections [57]. The former was achieved by using the remaining cross sections after subtracting the contribution represented by the observed photo-peak and its convolution by the detector response function, to be regarded as the contribution from unresolved overlapping contributions of small cross sections. The latter assumed that the decay through the first excited state almost represents the cascade decay contributions.
5 Magnetic dipole excitation
In this section, we present a study of magnetic dipole excitation of nuclei studied by the proton inelastic scattering experiment at RCNP. The target nucleus responds to the external magnetic field, similarly to the case of the electric field. The magnetic response of nuclei were historically studied by using polarized real-photon beam [33, 58] or by electron scattering [59]. The magnetic response is usually much weaker than the electric response. The asymmetry with respect to the polarization of the photon beam was used to decompose the electric and magnetic response of nuclei. The present experimental method, proton scattering, is sensitive only to the spin part of the magnetic response (spin-M1), as described in Section 1.2.2. Therefore, the results may contain different information on the nuclear response from the case of pure electromagnetic probes like photon-beam or electron scattering.
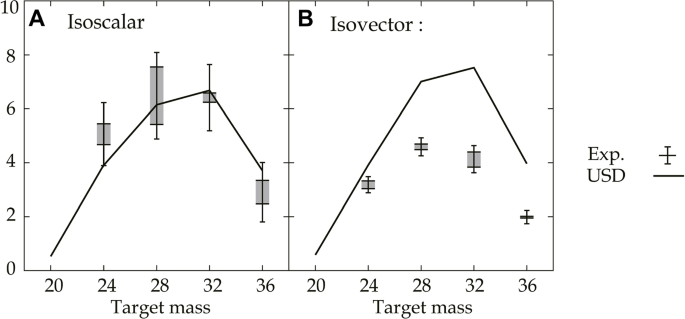
The cross sections of the spin-M1 excitations were either determined for the well-separated individual states or extracted for the continuum by MDA. The former method was applied to the data on self-conjugate (\(N=Z\)) even-even target nuclei in the sd-shell [60, 61]. The ground state of the target nuclei had a spin-parity of \(0^+\) and the isospin of \(T_i=0\). The spin-M1 excited states had a uniquely spin-parity of \(1^+\), and an isospin of \(T_f=0\) for IS (\(\Delta T=0\)) and \(T_f=1\) for IV (\(\Delta T=1\)) excitations under the assumption of isospin conservation. Thus, the strength distribution of the IS and IV isovector spin-M1 excitations could be studied independently. The shape of the angular distribution of the cross sections in the angular range of 0-14\(^\circ\) was used to identify the spin-parity and the isospin of the excited states. The maximum excitation energy of the analysis was 16 MeV due to the availability of unambiguous identification of each isolated excited state achievable with the highest excitation resolution of 17–20 keV.
The cross section at the scattering angle of \(0^\circ\) was determined for each excited state and was converted to the spin-M1 squared nuclear matrix elements (SNMEs), \(\left| M(\sigma )\right| ^2\) and \(\left| M(\sigma \tau )\right| ^2\), by applying the unit-cross section method [61]. The summed spin-M1 SNMEs up to 16 MeV were compared with the result of a shell model calculation using the USD effective interaction [62] in Fig. 7. The measured IV SNMEs were systematically smaller, generally referred to be quenching, than the model predictions. The tendency was consistent with the case observed in the study of Gamow-Teller transitions that were isospin-analog of the IV spin-M1 transitions. In contrast, the IS SNMEs were consistent in size with the theoretical prediction, i.e., not quenching. It was a new finding from the proton scattering study, and its theoretical interpretation is not converged yet [63,64,65].
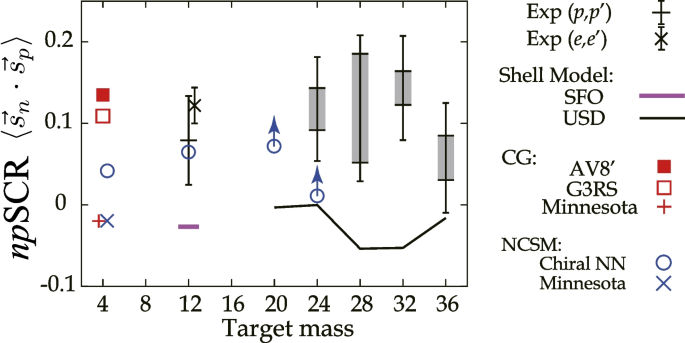
It is instructive to see the difference between the IS and IV SNMEs. Theoretically, the difference corresponds to the expectation value of the neutron-proton spin correlation function (npSCF) for the ground state wave function as [60]
when the sum of the SNMEs are taken to infinity. The experimental data showed a systematic trend of the npSCF to be positive, even though the uncertainty was large, while the shell-model prediction was zero or negative (Fig. 8).
The np spin correlation function determined by Eq. 19. The sum is taken up to the excitation energy of 16 MeV for the experimental data. The black line is the prediction by the shell model using the USD (\(A=20-36\)) [66] and SFO [67] (A=12) effective interactions. The other marks are ab initio type model calculations by non-core shell model (NCSM) [68] and correlated Gaussian CG) [69]. Adapted from [61]
A positive npSCF corresponds to a larger probability of having parallel spin-alignment between a neutron and a proton than anti-parallel. The positive experimental data might be caused by the IS spin-triplet pairing correlation or tensor correlation between a neutron and a proton in the ground state [64].
The spin-M1 strength for \(^{48}{\text {Ca}}\) and \(^{208}{\text {Pb}}\) was studied in Refs. [70, 71].
6 Gamma coincidence measurement of PDR
As recent studies, e.g. [72], indicated, the gamma coincidence measurement was a powerful tool to investigate the detailed information of the PDR. One of the physics cases at the CAGRA+GR campaign focused on this subject. A series of experiments were performed at RCNP with the clover detector array CAGRA.
F.C.L. Crespi et al. studied low-lying dipole strength of \(^{90,94}\)Zr via the (p, \(p'\gamma\)) reaction at 80 MeV and (\(\alpha\), \(\alpha '\gamma\)) at 120 MeV [73]. Target foils of \(^{90}\)Zr and \(^{94}\)Zr were located at the target position of the Grand Raiden spectrometer. The excitation energy spectra were measured using the missing mass method, while the de-excitation gamma rays were detected by CAGRA (E. Ideguchi, M.P. Carpenter, et al.: Germanium Clover detector array, CAGRA, in preparation). The angular correlation of the gamma rays and scattered particles was obtained for the two gamma-ray emission angles, 90\(^\circ\) and 135\(^\circ\), and for several bound states below the neutron separation energy. The \(\gamma\) angular correlation was sensitive to the multipole character of the gamma transition, and thus, it gave useful information for the spin-parity of each state. The result was compared with theoretical angular correlation calculated with the program ANGCOR (M. N. Harakeh and L. W. Put, unpublished) using the m-state population amplitudes obtained from DWBA calculations. The calculations well reproduced the angular correlations for the 2186-keV E2 transition and 6425-keV E1 transition for \(^{90}\)Zr, as well as the 919-keV E2 transition and 2846-keV E1 transition for \(^{94}\)Zr.
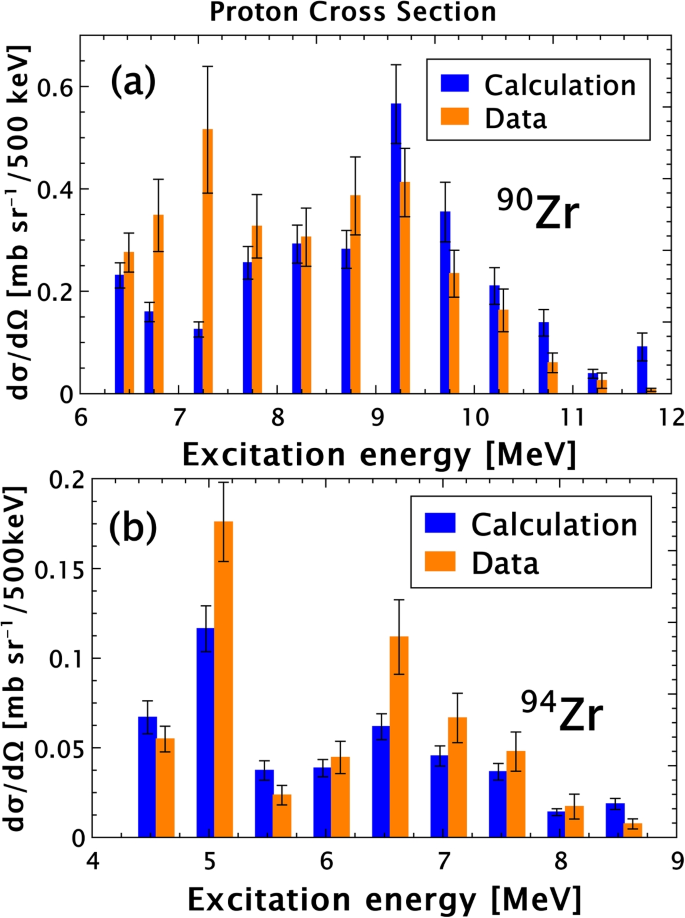
The proton inelastic cross sections were compared with DWBA calculations that were based on values of E1 energy weighted sum-rule (EWSR) strengths obtained from the (\(\alpha ,\alpha '\gamma\)) reactions in Fig. 9. The difference between the data and calculations indicated that between nuclear responses to probes, proton, and \(\alpha\), which enabled to discuss the mixture of isovector and isoscalar stregths in different states. In the case of \(^{90}\)Zr, the two data points near 7 MeV and the last data point at 11.5 MeV deviated from the calculations, indicating enhancement and suppression of the isovector strengths, respectively. In the case of \(^{94}\)Zr, two data points at 5 and 6.5 MeV were much larger than the calculations, suggesting enhancement of the isovector components below the neutron separation energy of \(^{94}\)Zr. In addition, a comparison between \(^{90}\)Zr and \(^{94}\)Zr results suggested that the ratio between the isovector and isoscalar components was different depending on the excitation energy. Further systematic measurements would define the properties of PDR, while it was indicated that the gamma coincidence measurements were a powerful approach in studying PDR.
The inelastic scattering cross sections of (\(p,p'\gamma\)) reactions are shown for a \(^{90}\)Zr and b \(^{94}\)Zr with orange bars [73]. The blue bars correspond to cross sections based on the DWBA calculations using values of the E1 EWSR strengths that were obtained from fitting of (\(\alpha ,\alpha '\gamma\)) cross sections. Comparison between the data and calculations indicated the difference between nuclear responses to proton and \(\alpha\)
7 Gamma emission from GDR and IVSDR for neutrino detection
The IV spin-dipole (IVSDR) excitation of nuclei, as well as the E1 excitation, is considered to be useful for detecting neutrinos by the neutral current (NC) nuclear excitation, which is sensitive to all the three neutrino species and their antiparticles. For example, the gamma rays emitted in the decay of the giant resonances can be used as a signal of the NC current nuclear excitation by incoming neutrinos in large-volume neutrino detectors [74].
The energy spectrum of the gamma rays and their emission probabilities are indispensable for simulating and calibrating the efficiency of neutrino detection. However, since experimental information is very scarce, one needs to rely on statistical decay calculations, even though the applicability of the statistical process for light nuclei, such as \(^{12}{\text {C}}\) or \(^{16}{\text {O}}\), is highly questionable.
The gamma rays emitted from the decay of the giant resonances excited in \(^{12}{\text {C}}\) [75] or \(^{16}{\text {O}}\) (T. Sudo et al.: γ rays from the giant resonances in 16O, submitted) were measured at RCNP by using the Grand Raiden spectrometer for detecting the inelastically scattered protons and NaI(Tl) detectors for emitted gamma rays.
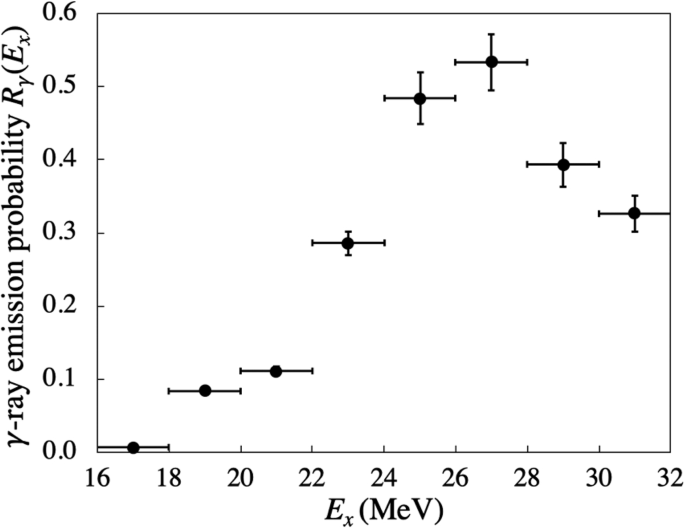
The result for \(^{12}{\text {C}}\) is shown in Fig. 10. The gamma emission probability reached up to \(\sim 50\)% at 27 MeV and decreased above it. The reason for the reduction at the higher excitation energy might be related to the opening of the two nucleon emission channel but is not fully understood yet.
Gamma emission probability from the giant resonances in \(^{12}{\text {C}}\) [75]
8 Photo-nuclear reaction of light nuclei (PANDORA project)
An international project PANDORA (Photo-Absorption of Nuclei and Decay Observation for Reactions in Astrophysics) [3] has been launched as a collaborative research among the experimental nuclear physics, theoretical nuclear physics, and astroparticle physics. The project aims at studying systematically the photo-nuclear reactions for light nuclei below a mass of A=60 both experimentally and theoretically. The primary application of the result is a precise prediction together with an estimation of the uncertainty of the photo-disintegration process of the ultra-high-energy cosmic rays (UHECRs) in intergalactic propagation.
The UHECRs were observed on Earth by detecting extended air showers at Pierre Auger (Auger) [76] and Telescope Array (TA) [77] observatories in the southern and northern hemispheres on Earth, respectively, up to above \(10^{20}\) eV. The origin, acceleration mechanism, and composition are, however, still in a mystery [78]. Recent observation data at Auger hinted that the UHECRs were atomic nuclei with an average mass between a proton and an iron nucleus. Since the primary energy loss process of the UEHCRs is due to the mass loss through the photo-disintegration process by the collision between the ultra-relativistic nucleus and cosmic microwave background (CMB) photons, accurate prediction of the photo-nuclear reactions is indispensable for understanding the evolution of the energy and mass spectra of the UHECRs, maximum travel distance, and the deflection by the intergalactic magnetic field.
However, the photo-nuclear reaction data, including the photo-absorption cross sections and the branching ratio of each decay channel, are quite scarce and unreliable in many cases. Theoretical predictions are also unsatisfactory in contrast to the case of heavier nuclei, where a nucleus shows a much smoother trend against the mass or the isospin.
In the PANDORA project, photo-absorption cross sections and proton, neutron, deuteron, alpha, and gamma decay branching ratios will be systematically studied by applying the virtual-photon excitation by proton scattering, described in this article, at RCNP in Japan and with a similar zero-degree setup at iThemba LABS [79] in South Africa, and by using high-brilliance LCS real-photon beams with VEGA [80, 81] at Extreme Light Infrastructure - Nuclear Physics (ELI-NP) in Romania, that will be available in the near future. The experiments are planned to start in 2023 at RCNP and iThemba LABS. Developments of theoretical models are ongoing for Antisymmetrised Molecular Dynamics (AMD) [82, 83], RPA with the density functional approach [84], Quasi-particle Phonon Model (QPM) [85, 86], Relativistic Nuclear Field Theory (RNFT) [87,88,89], large-scaler shell model [90], and ab initio type calculations together with a UHECR propagation simulation [91].
9 Summary
We highlighted several experimental works on the electric (E1) and spin-magnetic (spin-M1) dipole responses of nuclei studied by proton inelastic scattering experiments at forward angles, including zero degrees, at RCNP by using a proton beam at 295 or 392 MeV and the high-resolution magnetic spectrometer Grand Raiden.
The E1 polarizability was measured for \(^{208}{\text {Pb}}\) and several other nuclei. Constraint bands on the symmetry energy parameters, J and L, were extracted by using EDF model calculations. Low-lying E1 modes were studied in the context of PDR, which was theoretically predicted as a E1 oscillation of excess neutrons against the isospin-saturated core. It was indicated that the determination of the full B(E1) strength distribution was important for the study; a significant amount of the strength might be missing in NRF experiments. From the study of spin-M1 excitations in self-conjugate even-even nuclei in the sd-shell, it was found that the IS spin-M1 SNMEs was not quenched from theoretical prediction by the shell model in contrast to the case of the IV spin-M1 SNMEs that were quenched similar to the case of the analog GT transitions,
Gamma-coincidence measurements were performed by employing a clover germanium detector array (CAGRA), large volume LaBr\(_3\) detectors (SC\(\gamma\)LLA), or NaI(Tl) detectors for the study of isospin structure of the pygmy dipole resonances, gamma-decay to the ground state from the GDR, and gamma-emission probability for the giant resonances in \(^{12}{\text {C}}\) and \(^{16}{\text {O}}\) for neutral current neutrino detection.
Finally, a new project, PANDORA, was introduced aiming at a systematic study of photo-nuclear reactions and decay branching ratios of light nuclei for understanding the energy and mass evolution of ultra-high-energy cosmic rays during intergalactic propagation. We note that there are also several other studies, such as gamma-strength function [16, 92, 93] and analysis of nuclear level density [92,93,94] from high-resolution spectra, that were omitted in the review.