Since Feynman’s original proposal in the early 1980s [1], a growing amount of research has been conducted to develop large-scale, programmable quantum computers that promise to solve classically intractable problems. Although a variety of systems have been proposed to achieve this [2,3,4,5], practical issues such as noise and losses introduce errors that scale with system size, hampering physical implementations. Therefore, one approach of current experimental efforts has been the development of specialized devices aiming to unequivocally demonstrate quantum advantage, even when experimental imperfections are present.

To this end, recent developments use photonic networks implementing different computationally hard tasks [6,7,8,9]. Such devices are made entirely from linear optics such as polarizing beamsplitters, mirrors, and phase-shifters [4, 10], with optical parametric oscillators as the quantum source [11, 12]. Unlike cryogenic devices based on superconducting quantum logic gates [13, 14], these networks are operated at room temperature. Large size networks now claim quantum advantage [15,16,17,18], especially for a type of quantum computer called a Gaussian boson sampler that generates random bit outputs with a distribution that is exponentially hard to replicate at large network sizes.

This begs the question: how can one verify that large-scale experimental outputs are correct, when the device is designed to solve problems that no classical computer can solve in less than exponential time?

In this paper, we review theoretical methods that answer this for photonic network-based quantum computers. We especially focus on positive-P phase-space representations that can simulate non-classical states [19]. Here, we mean simulate in the sense of a classical sampling algorithm that replicates probabilities and moments to an accuracy better than experimental sampling errors, for the same number of samples. Such methods account for loss and decoherence. They are classical algorithms for standard digital computers. In addition, they are highly scalable, with polynomial run-time for large networks.

Other types of simulation exist, where the classical algorithm replicates the detection events of the experiment [20,21,22]. These become intractably slow for larger networks. The use of methods like this is to offer a way to define quantum advantage, meaning a quantum device performing tasks that are classically infeasible. Hence, we review the definitions of simulation in the literature including other approaches as well. There are also methods that simulate events quickly but approximately, up to a systematic error caused by the fact that the approximate method has a different probability distribution [23,24,25]. A comparison is made of different approaches that are proposed or used for these problems, including classical “faking” methods that replicate stochastic detection events with some degree of inaccuracy.

Positive-P methods are exactly equivalent to quantum moments in the large sample limit and are applicable to a variety of experimental networks. One example is the coherent Ising machine (CIM) [26, 27], which is used to solve NP-hard optimization problems by simulating an Ising model with a series of light pulses [9, 28, 29]. The largest experimental implementation of the CIM to date contains 100,000 modes [12]. This gives approximate solutions to hard max-cut problems three orders of magnitude faster than a digital computer. For such problems, typically no exact results are known. Therefore, these solutions can be hard to validate as well.

Gaussian boson sampling [30,31,32] experiments have seen impressive advancements in recent years. These specialized linear network quantum computers are used as random number generators, where the detected output photon counts correspond to sampling from the \(\#P\)-hard Hafnian or Torontonian distributions [7, 8, 33], which are either directly or indirectly related to the matrix permanent. While more specialized than quantum circuit devices, they are also somewhat more straightforward to implement and analyze theoretically.

Only a few years after the original theoretical proposals [7, 8, 33], multiple large-scale experiments have implemented GBS, with each claiming quantum advantage [15,16,17,18]. This rapid increase in network size has far outpaced direct verification methods [20,21,22], whilst other approximate methods [23, 24] typically cannot reproduce the higher-order correlations generated in linear photonic networks of this type.

In summary, we review progress on simulating binned correlations or moments of experimental GBS networks using the positive-P phase-space representation [30,31,32], as well as comparing this with other methods. We find that current experimental results disagree with the ideal, pure squeezed state model. However, agreement is greatly improved with the inclusion of decoherence in the inputs. When this decoherence is large enough, classical simulation is feasible [34, 35], and quantum advantage is lost. Despite this, recent experimental results demonstrate potential for quantum advantage in some of the reported datasets [32].

In order to present a complete picture, we also review the background theory of GBS, recent large scale experiments [15,16,17,18] and other proposed verification algorithms [20,21,22,23,24,25].

The original boson sampler introduced by Aaronson and Arkhipov [6] proposed a quantum computer that generates photon count patterns by randomly sampling an output state whose distribution corresponds to the matrix permanent. The computational complexity arises from sampling the permanent, which is a \(\#P\)-hard computational problem [36, 37].

However, practical applications of the original proposal have seen limited experimental implementations, since they require one to generate large numbers of indistinguishable single photon Fock states. Although small scale networks have been implemented [38,39,40], to reach a computationally interesting regime requires the detection of at least 50 photons [41, 42]. This is challenging to implement experimentally.

To solve this scalability issue, Hamilton et al. [7] proposed replacing the Fock states with Gaussian states, which can be more readily generated at large sizes. These types of quantum computing networks are called Gaussian boson samplers. They still use a non-classical input state, but one that is far easier to generate experimentally than the original proposal of number states.

2.1 Squeezed states

In standard GBS, N single-mode squeezed vacuum states are sent into an M-mode linear photonic network. If \(N\ne M\), the remaining \(N-M\) ports are vacuum states. If each input mode is independent, the entire input state is defined via the density matrix

\(\begin{aligned} \hat{\rho }^{(\text {in})}=\prod _{j}^{M}\left| r_{j}\right\rangle \left\langle r_{j}\right| . \end{aligned}\)

(1)

Here, \(\left| r_{j}\right\rangle =\hat{S}(r_{j})\left| 0\right\rangle\) is the squeezed vacuum state and \(\hat{S}(r_{j})=\textrm{exp}\left(r_{j}\left(\widehat{a}_{j}^{\dagger (\text {in})}\right)^{2}/2-r_{j}\left(\widehat{a}_{j}^{(\text {in})}\right)^{2}/2\right)\) is the squeezing operator [43,44,45]. We assume the squeezing phase is zero and \(\hat{a}^{\dagger (\text {in})}\) \(\left( \hat{a}_{j}^{(\text {in})}\right)\) is the input creation (annihilation) operator for the jth mode. The vacuum state \(\left| 0\right\rangle\) corresponds to setting \(r_{j}=0\) in the squeezing operator.

The ideal GBS assumes that inputs are pure squeezed states [46]. These non-classical states are characterized by their quadrature variance and are defined as [47, 48]

\(\begin{aligned} \Delta _{x_{j}}^{2}{} & {} =2\left( n_{j}+m_{j}\right) + 1 =e^{2r_{j}}\nonumber \\ \Delta _{y_{j}}^{2}{} & {} =2\left( n_{j}-m_{j}\right) + 1=e^{-2r_{j}}. \end{aligned}\)

(2)

Here, \(\Delta _{x_{j}}^{2}=\left\langle (\Delta \hat{x}_{j})^{2}\right\rangle =\left\langle \hat{x}_{j}^{2}\right\rangle -\left\langle \hat{x}_{j}\right\rangle ^{2}\) is the simplified variance notation for the input quadrature operators \(\hat{x}_{j}=\hat{a}_{j}^{(\text {in})}+\hat{a}_{j}^{\dagger (\text {in})}\) and \(\hat{y}_{j}=-i(\hat{a}_{j}^{(\text {in})}-\hat{a}_{j}^{\dagger (\text {in})})\), which obey the commutation relation \([\hat{x}_{j},\hat{y}_{k}]=2i\delta _{jk}\).

Squeezed states, while still satisfying the Heisenberg uncertainty principle \(\Delta _{x_{j}}^{2}\Delta _{y_{j}}^{2}=1\), have altered variances such that one quadrature has variance below the vacuum noise level, \(\Delta _{x_{j}}^{2}<1\). By the Heisenberg uncertainty principle, this causes the variance in the corresponding quadrature to become amplified well above the vacuum limit, \(\Delta _{y_{j}}^{2}>1\) [43, 49, 50]. Other squeezing orientations are available and remain non-classical so long as one variance is below the vacuum limit.

For pure squeezed states, the number of photons in each mode is \(n_{j}=\left\langle \hat{a}_{j}^{\dagger (\text {in})}\hat{a}_{j}^{(\text {in})}\right\rangle =\sinh ^{2}(r_{j})\), whilst the coherence per mode is \(m_{j}=\left\langle (\hat{a}_{j}^{(\text {in})})^{2}\right\rangle =\cosh (r_{j})\sinh (r_{j})=\sqrt{n_{j}\left( n_{j}+1\right) }\).

2.2 Input-output theory

Linear photonic networks made from a series of polarizing beamsplitters, phase shifters and mirrors act as large scale interferometers, and crucially conserve the Gaussian nature of the input state.

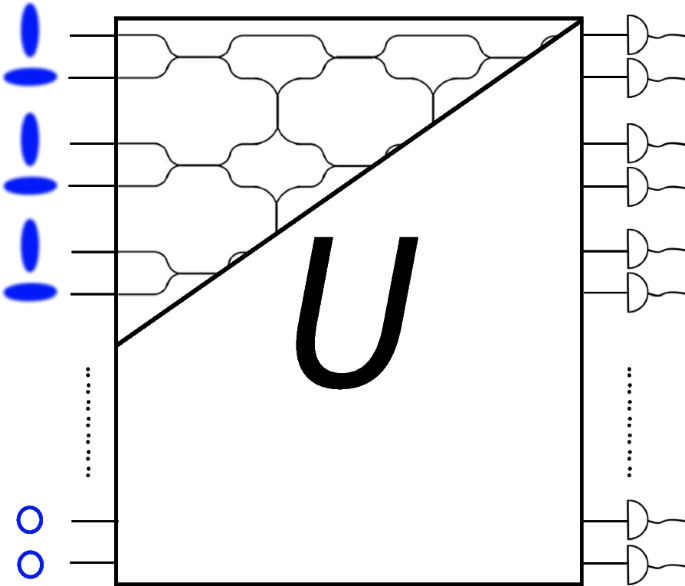
In the ideal lossless case, as seen in Fig. 1, photonic networks are defined by an \(M\times M\) Haar random unitary matrix \(\boldsymbol{U}\). The term Haar corresponds to the Haar measure, which in general is a uniform probability measure on the elements of a unitary matrix [51].

For lossless networks, input modes are converted to outputs following

\(\begin{aligned} \hat{a}_{k}^{(\text {out})}=\sum \limits _{j=1}^{M}U_{kj}\hat{a}_{j}^{(\text {in})}, \end{aligned}\)

(3)

where \(\hat{a}_{k}^{(\text {out})}\) is the output annihilation operator for the kth mode. Therefore, each output mode is a linear combination of all input modes.

Practical applications will always include some form of losses in the network, for example, photon absorption. This causes the matrix to become non-unitary, in which case it is denoted by the transmission matrix \(\boldsymbol{T}\), and the input-to-output mode conversion now contains additional loss terms [52, 53]:

\(\begin{aligned} \hat{a}_{k}^{(\text {out})}=\sum \limits _{j=1}^{N}T_{kj}\hat{a}_{j}^{(\text {in})}+\sum \limits _{j=1}^{M}B_{kj}\hat{b}_{j}^{(\text {in})}. \end{aligned}\)

(4)

Here, \(\hat{b}_{j}^{(\text {in})}\) is the annihilation operator for the jth loss mode whilst \(\boldsymbol{B}\) is a random noise matrix. The loss matrix conserves the total unitary of the system as \(\boldsymbol{T}\boldsymbol{T}^{\dagger }+\boldsymbol{B}\boldsymbol{B}^{\dagger }=\boldsymbol{I}\), where \(\boldsymbol{I}\) is the identity matrix.

Although linear networks are conceptually simple systems, they introduce computational complexity from the exponential number of possible interference pathways photons can take in the network. These are generated from the beamsplitters. As an example, the input ports of a 50/50 beamsplitter are defined as superpositions of the output modes:

\(\begin{aligned} \hat{a}_{1}^{\dagger (\text {in})}{} & {} =\frac{1}{\sqrt{2}}\left( \hat{a}_{3}^{\dagger (\text {out})}+\hat{a}_{4}^{\dagger (\text {out})}\right) \nonumber \\ \hat{a}_{2}^{\dagger (\text {in})}{} & {} =\frac{1}{\sqrt{2}}\left( \hat{a}_{3}^{\dagger (\text {out})}-\hat{a}_{4}^{\dagger (\text {out})}\right) . \end{aligned}\)

(5)

Classical states such as coherent and thermal states input into large-scale linear networks are readily simulated on a classical computer [34]. This leads to the question, why are non-classical states such as Fock and squeezed states computationally hard to simulate on large-scale photonic networks?

In short, non-classical states input into a linear network generate large amounts of quantum correlations, which are non-trivial to simulate classically if combined with photo-detection. Continuing with the beamsplitter example above, if input ports 1 and 2 now contain indistinguishable Fock states, as is the case with standard boson sampling, the input state can be written as

\(\begin{aligned} \left| 1,1\right\rangle _{1,2}=\frac{1}{\sqrt{2}}\left( \left| 2,0\right\rangle _{3,4}-\left| 0,2\right\rangle _{3,4}\right) . \end{aligned}\)

(6)

The absence of a \(\left| 1,1\right\rangle _{3,4}=\hat{a}_{3}^{\dagger (\text {out})}\hat{a}_{4}^{\dagger (\text {out})}\left| 0,0\right\rangle _{3,4}\) term means the output photons are bunched, that is, they are entangled and always arrive in pairs [54]. This phenomena is known as the Hong-Ou-Mandel (HOM) interference effect and is named after the authors who first observed this phenomena [55].

If input ports 1 and 2 have input-squeezed vacuum states, one generates two-mode Einstein-Podolsky-Rosen (EPR) entanglement in the quadrature-phase amplitudes [56, 57]. More details, including a summary of the derivation, can be found in [31, 58].

Gaussian boson sampling schematic where \(N\subset M\) single-mode squeezed states of different polarizations (blue ellipses) are sent into a lossless linear photonic network where the remaining \(N-M\) inputs are vacuum states (blue outlined circles). The linear network is created from a series of phase-shifters and beamsplitters, represented here in a circuit diagram format. This generates an exponential number of interference pathways. Mathematically, the network is defined by an \(N\times M\) Haar random unitary \(\boldsymbol{U}\). Output photon patterns are then obtained using either PNR or click detectors

 Full size image 

2.3 Photon counting

In GBS experiments, photon count patterns, denoted by the vector \(\boldsymbol{c}\), are generated by measuring the output state \(\hat{\rho }^{(\text {out})}\). The corresponding distribution changes depending on the type of detector used.

The original proposal for GBS [7] involved normally ordered photon-number-resolving (PNR) detectors that can distinguish between oncoming photons and implement the projection operator [54, 59]

\(\begin{aligned} \hat{p}_{j}(c_{j})=\frac{1}{c_{j}!}:\left( \hat{n}'_{j}\right) ^{c_{j}}e^{-\hat{n}'_{j}}:. \end{aligned}\)

(7)

Here, \(:\dots :\) denotes normal ordering, \(c_{j}=0,1,2,\dots\) is the number of counts in the jth detector and \(\hat{n}'_{j}=\hat{a}_{j}^{\dagger (\text {out})}\hat{a}_{j}^{(\text {out})}\) is the output photon number. Practically, a PNR detector typically saturates for a maximum number of counts \(c_{\text {max}}\), the value of which varies depending on the type of PNR detector implemented.

When the mean number of output photons per mode satisfies \(\left\langle \hat{n}'_{j}\right\rangle \ll 1\), PNR detectors are equivalent to threshold, or click, detectors which saturate for more than one photon at a detector. Click detectors are described by the projection operator [59]

\(\begin{aligned} \hat{\pi }_{j}(c_{j})=:e^{-\hat{n}'_{j}}\left( e^{\hat{n}'_{j}}-1\right) ^{c_{j}}:, \end{aligned}\)

(8)

where \(c_{j}=0,1\) regardless of the actual number of photons arriving at the detector.

In situations where \(\left\langle \hat{n}'_{j}\right\rangle \gg 1\), click detectors cannot accurately discriminate between the different numbers of oncoming photons. However, by sending photons through a demultiplexer (demux) before arriving at the detector, the output pulses of light become "diluted" such that the photon number is small enough to be accurately counted using click detectors [60, 61]. In this approach, the demux acts as a type of secondary optical network of size \(1\times M_{S}\), where \(M_{S}\) is the number of secondary modes. For output photons to become sufficiently dilute, one must satisfy \(M_{S}\gg \left\langle \hat{n}'_{j}\right\rangle\) [60,61,62]. When this is the case, the detectors can be thought of pseudo-PNR (PPNR), because the click detectors are accurately measuring photon counts, thus becoming equivalent to PNR detectors [62].

The computational complexity of GBS arises in the probabilities of count patterns \(\boldsymbol{c}\). These probabilities are determined using a straightforward extension of the projection operators for both PNR and click detectors. In the case of PNR detectors, the operator for a specific photon count pattern is

\(\begin{aligned} \hat{P}(\boldsymbol{c})=\bigotimes _{j=1}^{M}\hat{p}_{j}(c_{j}), \end{aligned}\)

(9)

the expectation value of which corresponds to the \(\#P\)-hard matrix Hafnian [7, 33]

\(\begin{aligned} \left\langle \hat{P}(\boldsymbol{c})\right\rangle \approx |\text {Haf}(\boldsymbol{D}_{S})|^{2}. \end{aligned}\)

(10)

Here, \(\boldsymbol{D}_{S}\) is the sub-matrix of \(\boldsymbol{D}=\boldsymbol{T}\left( \bigoplus _{j=1}^{M}\tanh (r_{j})\right) \boldsymbol{T}^{T}\), corresponding to the channels with detected photons, where the superscript T denotes the transpose of the lossy transmission matrix.

The Hafnian is a more general function than the matrix permanent, although both are related following [7, 33]

\(\begin{aligned} \text {perm}(\boldsymbol{D})=\text {Haf}\left( \begin{array}{cc} 0 &{} \boldsymbol{D}\\ \boldsymbol{D}^{T} &{} 0 \end{array}\right) . \end{aligned}\)

(11)

Therefore, one of the advantages of GBS with PNR detectors is that one can compute the permanent of large matrices from the Hafnian instead of performing Fock state boson sampling.

For click detectors, the operator for a specific binary count pattern \(\boldsymbol{c}\) is

\(\begin{aligned} \hat{\Pi }(\boldsymbol{c})=\bigotimes _{j=1}^{M}\hat{\pi }_{j}(c_{j}), \end{aligned}\)

(12)

whose expectation value corresponds to the Torontonian [8]

\(\begin{aligned} \left\langle \hat{\Pi }(\boldsymbol{c})\right\rangle =\text {Tor}(\boldsymbol{O}_{S}), \end{aligned}\)

(13)

where \(\boldsymbol{O}_{S}\) is a matrix constructed from the covariance matrix of the output state. The Torontonian has also been shown to be \(\#P\)-hard to compute, and is related to the Hafnian [8].

2.4 Experimental progress

Only a few short years after the original proposal of GBS with click detectors [8], the first large-scale experimental network, called Jiuzhang 1.0, was implemented by Zhong et al. [15]. In this experiment, 25 two-mode squeezed states, corresponding to \(N=50\) single-mode squeezed states, were created by driving nonlinear crystals with transform-limited laser pulses, which is the standard process of parametric down-conversion. The polarization of each input squeezed state alternates from horizontal to vertical for each spatial mode as illustrated in Fig. 1.

Once generated, the squeezed states were sent into a lossy \(M=100\) mode linear network made from over 300 beamsplitters and phase-shifters. The network is separated into two stages: The first consists of three-dimensional five-layer triangular and rectangular interferometers [63], similar to the network implemented in the Fock state boson sampling experiment of Wang et al. [64]. The squeezed photons propagate through the triangular layers, allowing photons of the same polarization within the same layer to interfere. Cross-layer photon interference then occurs within the rectangular layers however, interference of photons with different polarizations does not occur until the second stage. In this stage a series of polarizing beamsplitters in the form of an array of Mach-Zehnder-like interferometers causes photons of all polarizations to interfere [15].

Jiuzhang 1.0 generated over 50 million binary count patterns from superconducting nano-wire click detectors in \(\approx 200\text {s}\). The experimentalists estimated it would take Fugaku, the largest supercomputer at the time, 600 million years to generate the same number of samples using the fastest exact classical algorithm at the time [20]. Exact samplers are algorithms designed to replicate an experiment by directly sampling the Torontonian or Hafnian using a classical supercomputer. When experiments claim a quantum advantage, they typically do so by comparing the run-time of the experiment with such exact samplers.

The algorithm implemented in [20] uses a chain rule sampler that samples each mode sequentially by computing the conditional probability of observing photons in the kth mode given the photon probabilities of the previous \(k-1\)th modes. The computational complexity of this algorithm scales as \(\mathcal {O}(N_{D}^{3}2^{N_{D}})\) where \(N_{D}=\sum _{j=1}^{M}c_{j}\) is the total number of detected photon counts. Due to this scaling with detected counts and system size, more recent experiments aim to beat these exact samplers by increasing the number of observed counts. The mean number of counts per pattern in Jiuzhang 1.0 was \(\approx 41\), and the largest number of counts in a single pattern was 76.

Shortly after this initial experiment, in order to reduce the probability of an exact sampler replicating the experiment, Zhong et al. [16] implemented an even larger GBS network, named Jiuzhang 2.0, which increased the number of modes to \(M=144\). The general fabrication process of the network remained largely the same as Jiuzhang 1.0, although the number of interferometer layers and optical elements increased. Multiple experiments were performed for different input laser powers and waists, producing an increase in the number of observed clicks, with a mean click rate of \(\approx 68\) and a maximum observed click number of \(N_{D}=113\).

At the same time, in classical computing, the increased probability of multiple photons arriving at the same detector was exploited by Bulmer et al. [22] to improve the scaling of the chain rule sampler, achieving \(\mathcal {O}(N_{D}^{3}2^{N_{D}/2})\) for GBS with both PNR and click detectors. Despite this apparently modest improvement, it was estimated that generating the same number of samples as Jiuzhang 1.0 on Fugaku would now only take \(\sim 73\) days [22]. Due to the substantial speed-up over previous exact algorithms [20, 21], it was predicted that experiments using either PNR or click detectors needed \(N_{D}\gtrsim 100\) to surpass exact samplers [22].

To reduce the probability of multiple photons arriving at a single detector, Deng et al. [18] added a \(1\times 8\) demux to the output modes of Jiuzhang 2.0, dubbing this upgraded network Jiuzhang 3.0. The demux is made of multiple fiber loop beamsplitters that separate photons into four temporal bins and two spatial path bins and aims to ensure \(\left\langle \hat{n}'_{j}\right\rangle \lesssim\ 1\), increasing the likelihood the click detectors are accurately counting the oncoming photons. This simple addition generated patterns with almost double the largest number of clicks obtained in Jiuzhang 2.0, with one experiment observing a maximum of \(N_{D}=255\) with a mean click number of more than 100.

The linear networks implemented in the three experiments above are all static, that is, once the networks have been fabricated, one cannot reprogram any of the internal optics. This has the advantage of circumventing the exponential accumulation of loss that arises from increased depth [17, 65], although one sacrifices programmability.

To this end, Madsen et al. [17] implemented a programmable GBS called Borealis where N-squeezed state pulses are generated at a rate of \(6\text {MHz}\) from an optical parametric oscillator in a cavity. Following from an initial proposal by Deshpande et al. [65], the linear network is formed using three fiber delay line loops attached to a variable beamsplitter (VBS), which is constructed from a programmable phase-shifter, polarizing beamsplitters and a Pockels cell, which simply modulates the polarization. The input pulses enter each VBS sequentially, the first VBS causes pulses in the time range \(\tau =1/(6\text {MHz})\) to interfere, which simply corresponds to interference between photons inside the VBS and the next on-coming pulse. The second and third VBS allow pulses in the range \(6\tau =1\text {MHz}\) and \(36\tau =6\text {MHz}\) to interfere, respectively. Photons output from the final fiber loop are then sent into a \(1\times 16\) demux and then counted by 16 PNR detectors, which are superconducting transition edge sensors.

Transition edge sensors are a type of highly efficient PNR detector that contains a very low dark count rate [66, 67]. They extract energy information from oncoming light, where each detection event is represented as a time-varying voltage signal (see figures in Ref. [66] for an example). Therefore, the larger the number of photons in an output pulse, the larger the energy, and hence, the observed voltage signal. However, since each detector operates at some baseline temperature, a large voltage signal affects the cooldown time of each detector. To extract photon numbers from the observed voltage-time graph, Madsen et al. [17] use the method outlined in Morais et al. [66] which requires measuring the area, height, length, and maximum slope of the voltage-time output. In order to do this accurately, the detector is required to reach the cooldown temperature before an additional pulse arrives, or else one cannot distinguish between pulses.

This is achieved by the demux, which is constructed using a series of beamsplitters. The demux not only partially “dilutes” the number of photons in each output pulse, as \(c_{\text {max}}=13\), but it also delays the output pulses as the cooldown time for each detector is \(\approx 50-100\text {kHz}\) [17]. This ensures an accurate determination of photon numbers.

The two largest networks using this setup sent \(N=216\) and \(N=288\) input pulses into the network, detecting a mean photon number of \(\approx 125\) and \(\approx 143\), respectively. However, this network was more susceptible to losses than the previous Jiuzhang systems [18, 25].

The rapid growth of experimental networks has spurred a parallel increase in the number of algorithms proposed for the validation and/or simulation of these networks. Due to this, there are some inconsistencies in the literature on the language used to define a simulator which runs on a classical computer. Therefore, we clarify the definitions of the various classical simulators proposed for validation used throughout the rest of the review.

We first emphasize that a classical algorithm or classical simulator is any program designed to run on a digital computer, be that a standard desktop or supercomputer. The current algorithms proposed to validate GBS can be defined as either strong or weak classical simulators [68]. There is a large literature on this topic, starting from early work in quantum optics.

Weak classical simulators parallel the quantum computation of experimental networks by sampling from the output probability distribution [69]. Algorithms that sample from the full Torontonian or Hafnian distributions are exact samplers [20,21,22], as outlined above, and all known exact algorithms are exponentially slow. There are faster but approximate algorithms producing discrete photon count patterns that are typically called “faked” or “spoofed” patterns. Some of these generate fake patterns by sampling from the marginal probabilities of these distributions [23, 24], in which case they are called low-order marginal samplers. Such low-order methods are only approximate, since they don’t precisely simulate higher-order correlations [23, 24].

In contrast, strong classical simulators are a type of classical algorithm that evaluates the output probability distribution, be that the full or marginal probabilities, of a GBS with multiplicative accuracy, in time polynomial in the size of the quantum computation [69, 70].

Phase-space simulators have a similarity to strong classical simulators, because the samples, which are produced with a stochastic component representing quantum fluctuations, are used to compute probabilities or moments of the ideal distribution. Positive-P phase-space simulations have been widely used in quantum optics for this reason [19, 71,72,73,74,75]. While the sampling precision is not multiplicative, it is better than the experimental precision of GBS at the same sample number, which is sufficient for validation. By approximating the inputs as classical states, one can also use phase-space methods to produce fake patterns [32], in which case they are called a classical P-function sampler, as explained below.

For non-classical inputs, one can generate probabilities but not count patterns using phase-space methods: since there are no known algorithms to generate counts efficiently from non-classical phase-space samples.

3.1 Exact classical simulation

There are a number of “exact” classical simulation methods that generate equivalent photon counts, where we use quotes for “exact,” because even these methods have round-off errors due to finite arithmetic. These algorithms are all exponentially slow [20,21,22]. It is known that the non-classicality of the squeezed input states of GBS is essential to providing quantum advantage in the GBS experiments, since classical states which have a positive Glauber-Sudarshan P-representation [76, 77] are known to have classically simulable photon counts. This will be treated in Section (3.2.2). However, the non-Gaussianity arising from the photon-detection measurement process is also important.

This is because the measurement set-up where quadrature-phase-amplitude measurements are made on a system described by Gaussian states can be modeled by a positive Wigner function, and hence, becomes classically simulable [34, 35]. Gaussian states are defined as those with a Gaussian Wigner function. We note that squeezed states, while non-classical, are Gaussian states. Examples of the classical simulation of entanglement for systems with a positive Wigner function are well known [78,79,80,81,82,83].

The role of the measurement set-up in GBS is clarified by the work of Chabaud, Ferrini, Grosshans, and Markham [69] and Chabaud and Walschaers [70]. These authors illustrate a connection between quantum advantage and the non-Gaussianity of both the input states and measurement set-up. In [69], conditions sufficient for the strong simulation of Gaussian quantum circuits with non-Gaussian input states are derived. Non-Gaussian states are those for which the Gaussian factorization of correlation functions is not applicable [84].

By demonstrating a mapping between bosonic quantum computation and continuous-variable sampling computation, where the measurement comprises a double quadrature detection, Chabaud and Walschaers [70] adapt classical algorithms derived in [69] to derive a general algorithm for the strong simulation of bosonic quantum computation, which includes Gaussian boson sampling. They prove that the complexity of this algorithm scales with a measure of non-Gaussianity, the stellar rank of both the input state and measurement set-up. This enables a quantification of non-Gaussianity, including from the nature of the measurement, as a resource for achieving quantum advantage in bosonic computation.

3.2 Approximate classical simulation

3.2.1 Low-order marginal samplers

Recent experiments have surpassed the threshold of applicability of exact samplers [16,17,18]. Even for experiments below this threshold [15], the computation time can still be very long and resource intensive. Therefore, approximate methods that are more readily scaled to larger sizes have been proposed. These cannot validate GBS, but they are useful in quantifying a computational advantage.

One approach presented by Villalonga et al. [23], exploits the computational efficiency of computing low-order marginal probabilities of the ideal GBS distribution to generate photon count patterns by sampling from a distribution that contains the correct low-order marginals. We note that the relevant marginal probabilities must first be evaluated before sampling.

Two methods are implemented to compute marginals, which take the form of multivariate cumulants, also called connected correlations or Ursell functions. The first method corresponds to a Boltzmann machine (BM) and computes pattern probabilities of the form [23]

\(\begin{aligned} \left\langle \hat{\Pi }(\boldsymbol{c})\right\rangle{} & {} =\frac{1}{Z}\textrm{exp}\left( \sum \limits _{i}\lambda _{i}\hat{\pi }_{i}(c_{i})+\sum \limits _{i

(14)

where Z is the partition function that normalizes the distribution and \(\lambda _{i},\lambda _{i,j},\dots\) are parameters computed using a mean-field approximation.

Each term in the exponent corresponds to a marginal probability of the ideal distribution, where a BM spoofer using only the first two summations was implemented due to scalability. The BM method is only applicable to GBS with click detectors, where faked binary patterns are obtained via Gibbs sampling [23].

The second method uses a greedy heuristic to generate discrete binary patterns with approximately correct second and third-order marginals. This algorithm scales exponentially with the desired order of the marginal and the length of the patterns, which are typically equal to the number of modes. Although the greedy method was originally developed for GBS with click detectors, it has since been extended to PNR detectors [17].

Faked patterns generated from both methods were compared to experimental samples from Jiuzhang 1.0 and 2.0. The best comparison results came from computing the total variation distance difference

\(\begin{aligned} \Delta \delta =\delta _{m}-\delta _{e}, \end{aligned}\)

(15)

where \(\delta _{m}\) is the total variation distance between pattern probabilities of the ideal distribution and the marginal spoofers, and \(\delta _{e}\) is the total variation distance between experiment and ideal.

Since computing pattern probabilities is computationally challenging, comparisons were limited to only 14 modes. However, although the first-order BM sampler was always beaten by the experiment, faked samples generated from the second-order BM and second and third-order greedy algorithms were closer to the ideal distribution than the experiment.

Comparisons of the cross-entropy measure, which is a widely used quantum advantage benchmark in random circuit sampling quantum computers [13, 85, 86], were also performed by Villalonga et al. [23]. It remains an open question whether this is a useful measure for boson sampling networks [24].

In general, if experimental samples obtain a smaller cross entropy than the spoofer, there is evidence of computational advantage. As was the case for the total variation distance difference, when compared to samples from the first-order BM, experimental samples were immediately larger, but for all other spoofers results were mixed, with all samples obtaining a similar cross entropy to the experiment [23].

An algorithm introduced by Oh et al. [24] was specifically designed to spoof the cross entropy measure of GBS networks using up to second-order marginal probabilities. This algorithm produced samples that successfully spoofed the small scale test networks in Ref. [17], but became too computationally demanding to spoof larger scale networks that claim quantum advantage [15,16,17].

3.2.2 Classical P-function samplers

Practical implementations of GBS will inevitably produce decoherence and losses. These may arise within the network, as discussed above, or in the input states as discussed in subsection 4.2. For large enough decoherence and loss, either the inputs, outputs or both are transformed to classical states [35, 52].

For such classical states, GBS loses its quantum advantage and an efficient classical simulation is possible. This was first shown by Rahimi-Keshari et al. [34] for Fock state boson sampling and later extended to GBS by Qi et al. [35], although the fundamental ideas are much older than this [87]. In both cases, the condition for classical simulation hinges on whether the resulting phase-space output distribution, simulated using a set of experimental inputs, was non-negative. These conditions hinge on the well-known result that, for some states, the Glauber-Sudarshan and Wigner representations produce negative distributions on phase space [54, 88], which is why they are typically referred to as quasi-probability distributions.

We define any classical algorithm that samples from the output distribution of a classical state GBS as a classical GBS sampler. Although the most commonly tested classical state is the fully decoherent thermal state, it is an extreme case and and has been thoroughly disproved for all current experimental networks [15,16,17,18]. However, a more realistic scenario is a classical approximation to pure squeezed states.

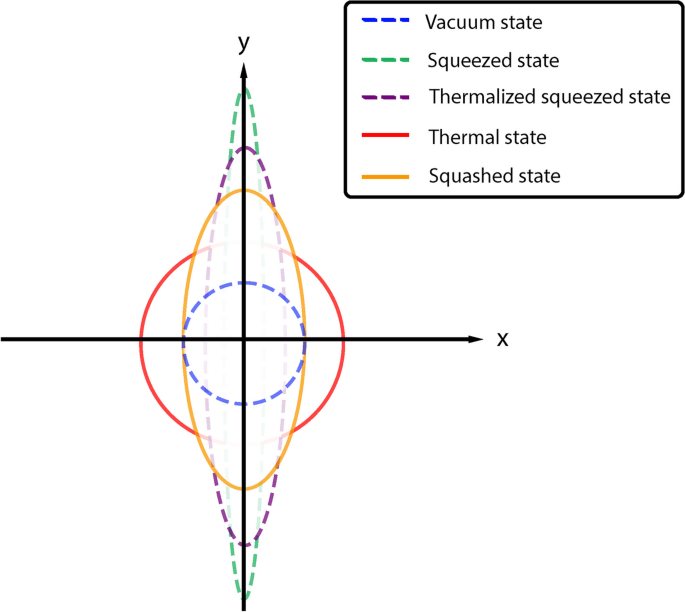
Two such states have recently been proposed called squashed and squished states [18, 89]. Unlike thermal states, which have a quadrature variance of \(\Delta _{x_{j}}^{2}=\Delta _{y_{j}}^{2}\), squashed and squished states maintain the unequal variances of squeezed states (see Fig. 2 for a diagram of the variances for different states). Despite this, decoherence may cause the once squeezed quadrature variance to become \(\Delta _{x_{j}}^{2}=1\), whilst \(\Delta _{y_{j}}^{2}>1\). Therefore, squashed and squished states are classical states. No true squeezing occurs, since neither variance is below the vacuum limit. We note that the difference between these two states is that squished states must contain the same mean number of photons as the input squeezed state [18], whereas the squashed state photon number can vary.

Comparisons of all experimental networks with simulated thermal states have, expectedly, failed [15,16,17,18]. However, Juizhang 1.0 data was shown to have a large degree of input decoherence [30], and hence simulated squashed states were shown to model samples from Jiuzhang 1.0 as well as the theoretical ideal distribution for some statistical tests [89]. An efficient phase-space sampler, which can generate binary patterns for any classical input state, later showed that squashed state count patterns were closer to the simulated ideal distribution than the experimental data set in Jiuzhang 2.0 that claims quantum advantage [32]. This method is reviewed in more detail in section 4. The most recent GBS experiments with PNR and click detectors, Borealis and Jiuzhang 3.0, produced outputs that were closer to the ideal than simulated squashed and squished states, although squished states have only been tested against samples from Jiuzhang 3.0 to date.

The classical GBS samplers implemented in these tests assume either all \(N\subset M\) inputs or all M outputs are classical states. A more physically realistic scenario is one where the inputs and/or outputs are mixtures of classical and quantum states. In order to model this, a classical sampler that scales with the loss rate \(\eta\) of the linear network was introduced by Oh et al. [25].

The aim of this algorithm is to simulate the output covariance matrix \(\boldsymbol{V}_{p}\) of a pure squeezed state GBS using a tensor network method. This covariance matrix arises from a decomposition of the actual output covariance matrix \(\boldsymbol{V}=\boldsymbol{W}+\boldsymbol{V}_{p}\), where \(\boldsymbol{W}\ge 0\) is a random displacement matrix arising from classical photons in the outputs.

As outlined in the previous subsection, the computational complexity of computing the ideal GBS, corresponding to \(\boldsymbol{V}_{p}\) in this case, scales with the number of system modes and hence detected photons. However, only non-classical output photons contribute to this computational complexity. Therefore, if more experimental output photons are classical rather than non-classical, the matrix \(\boldsymbol{W}\) will dominate the computation of \(\boldsymbol{V}\) [25], which one should then be able to simulate efficiently.

This is the general principle of the algorithm implemented by Oh et al. [25], where the number of non-classical output photons is computed from the actual squeezing parameter \(s=-1/2\ln (1-\eta )\). Clearly, as the loss rate increases, the non-classical photons decrease, in turn causing the number of classical photons to increase, allowing \(\boldsymbol{W}\) to dominate the output covariance matrix.

Samples obtained from this method were used to calculate the total variation distance and cross-entropy for the small-scale test networks of Ref. [17], as well as second and higher-order cumulants for larger-scale networks [15,16,17,18]. In all cases, samples produced from this classical sampler were closer to the ideal distributions than all the experiments, highlighting the extent to which the loss rate \(\eta\) plays a role in affecting claims of quantum advantage in the current generation of GBS.

The effect of losses and noise was also investigated by Mendes et al. [90], which proposed using the Lambert-Tsallis \(W_{q}\)-function to determine the randomness of the observed photon counts without actually computing the output probability distribution.

The \(W_{q}\)-function was used to determine the randomness of output photon patterns, with counts from an \(8\times 8\) Haar random unitary with input states having equal squeezing parameters serving as a baseline test [90]. When the input squeezing parameters and detector efficiency were altered, it was shown that one could distinguish samples from the two systems because the randomness measured by the disentropy was altered.

A diagram of the quadrature variance for different states. The vacuum state (blue dashed line) has variance \(\Delta _{x_{j}}^{2}=\Delta _{y_{j}}^{2}=1\) and arises from the Heisenberg uncertainty principle as the minimum uncertainty state. When \(\Delta _{x_{j}}^{2}<1,\,\Delta _{y_{j}}^{2}>1\) one obtains the non-classical pure squeezed state (green dashed line) or the thermalized squeezed state (purple dashed line), which has a larger variance for the squeezed quadrature than pure squeezing but remains below the vacuum limit. The classical thermal state (solid red line) has variance \(\Delta _{x_{j}}^{2}=\Delta _{y_{j}}^{2}>1\), while although the squashed state has variance \(\Delta _{x_{j}}^{2}\ne \Delta _{y_{j}}^{2}\), neither squeezing is below the vacuum limit as, in this case, \(\Delta _{x_{j}}^{2}=1,\,\Delta _{y_{j}}^{2}>1\).

 Full size image 

One of the many open questions in GBS research is how to efficiently validate large-scale experimental networks. The exact methods reviewed above either suffer from scalability issues [20,21,22], or else they do not simulate higher-order correlations [23] due to computational complexity. Due to the rapid growth of experimental networks, even higher-order correlations will be produced due to the increase in interference pathways. The requirement of a simulation method that validates a quantum computer is that it allows the computation of measurable probabilities with an accuracy at least equal to the experimental sampling error.

Such correlations and probabilities play an increasingly important role in characterization of the output distribution [91], even when losses are present [53, 92], despite their increased sensitivity to decoherence. Therefore, scalable methods are needed that simulate higher-order correlations without performing the impractical \(\#P\)-hard direct computation of the count samples. To this end, we review recent theoretical methods that simulate grouped count probabilities (GCPs) of GBS networks using the normally ordered positive-P phase-space representation.

Currently, these methods can be used for networks with click detectors, and have successfully been applied to compare theory and experiment for samples from Jiuzhang 1.0 [30] and Jiuzhang 2.0 [32]. We emphasize that the positive P-representation does not produce discrete count patterns. However, the simulated output distributions have identical moments to the ideal GBS distributions.

We first outline the necessary background theory on phase-space representations, focusing on normally ordered methods, and GCPs before briefly reviewing simulation results for data from Jiuzhang 1.0. These results were initially presented in [30], but were obtained by simulating single-mode squeezed states as opposed to two-mode squeezed states, due to ambiguities in the public dataset. The results are corrected here, but this does not change the conclusions presented in [30], as it only has a small effect on the ideal GBS distribution comparisons and the specific fitting parameter values.

For more details on the phase-space method, the interested reader is referred to Refs. [30,31,32], whilst the efficient phase-space code package, xQSim, can be downloaded from public domain repositories [93].

4.1 Phase-space methods

Originally developed by Wigner for symmetrically ordered operators [94], phase-space representations establish a mapping between quantum operators of different orderings to probability distributions defined on the classical phase-space variables of position and momentum [54, 95], which are more commonly rewritten in terms of the complex coherent state amplitude vectors \(\boldsymbol{\alpha }\), \(\boldsymbol{\alpha }^{*}\).

Moyal [96] later showed how one can use these methods to compute the dynamics of operators. Due to this, phase-space representations are frequently used to compute the operator master equation [95, 97], which for some representations, corresponds to the second-order Fokker-Planck equation (FPE), which is commonly used in statistical mechanics.

The FPE in turn, can be mapped to a stochastic differential equation (SDE) that introduces randomly fluctuating terms and, for some real or complex vector \(\boldsymbol{a}\), takes the general form [98]

To simulate GCPs in phase space, input stochastic amplitudes \(\boldsymbol{\alpha }\), \(\boldsymbol{\beta }\) corresponding to the phase-space distribution of the input state \(\hat{\rho }^{(\text {in})}\) must first be generated. However, although pure squeezed states are the theoretical “gold standard” of GBS, practically they are challenging to create in a laboratory and inevitably decoherence will arise from equipment.

5.1 Decoherent input states

A more realistic model is one that includes decoherence in the input state. Such a model was proposed in [30] and assumes the intensity of the input light is weakened by a factor of \(1-\epsilon\) while adding \(n_{j}^{\text {th}}=\epsilon n_{j}\) thermal photons per mode. The number of input photons per mode remains unchanged from the pure squeezed state definition, but the coherence of photons is now altered to \(\tilde{m}=(1-\epsilon )m_{j}\). To account for possible measurement errors, a correction factor t is also applied to the transmission matrix, to improve the fit to the simulated distribution.

The advantage of this decoherence model, which is a type of thermal squeezed state [47, 108], is that it allows a simple method for generating phase-space samples for any Gaussian state following

\(\begin{aligned} \alpha _{j}{} & {} =\frac{1}{2}\left( \Delta _{x_{j}}w_{j}+i\Delta _{y_{j}}w_{j+M}\right) \nonumber \\ \beta _{j}{} & {} =\frac{1}{2}\left( \Delta _{x_{j}}w_{j}-i\Delta _{y_{j}}w_{j+M}\right) , \end{aligned}\)

(26)

where \(\left\langle w_{j}w_{k}\right\rangle =\delta _{jk}\) are real Gaussian noises that model quantum fluctuations in each quadrature and

\(\begin{aligned} \Delta _{x_{j}}^{2}{} & {} =2(n_{j}+\tilde{m}_{j})\nonumber \\ \Delta _{y_{j}}^{2}{} & {} =2(n_{j}-\tilde{m}_{j}), \end{aligned}\)

(27)

are the thermal squeezed state quadrature variances.

As \(\epsilon \rightarrow 1\) the inputs become classical, since \(\Delta _{x_{j}}^{2},\,\Delta _{y_{j}}^{2}\ge 1\), but small amounts of thermalization cause the inputs to remain non-classical described, for example, by a squeezing of \(\Delta _{x_{j}}^{2}<1\). So long as the state is Gaussian, one can model a variety of inputs, both classical and non-classical, by simply varying \(\epsilon\), where \(\epsilon =0\) corresponds to a pure squeezed state and \(\epsilon =1\) to a thermal state. We note that this sampling method generates single-mode states. To simulate GBS with two-mode squeezed state inputs, as is the case with the Jiuzhang experiments, the N single-mode states are interfered using the matrix \(\boldsymbol{B}=\bigoplus _{k=1}^{N/2}U_{k}\) [89], where \(U_{k}\) is a unitary 50/50 beamsplitter matrix.

The input stochastic samples are also straightforwardly extended to non-normally ordered representations, as outlined in detail in [30,31,32].

Performing the summation over binary patterns can now be efficiently simulated in phase-space using the multi-dimensional inverse discrete Fourier transform [30]

\(\begin{aligned} \mathcal {G}_{\boldsymbol{S}}^{(n)}\left( \boldsymbol{m}\right) =\frac{1}{\prod _{j}(M_{j}+1)}\sum \limits _{\boldsymbol{k}}\tilde{\mathcal {G}}_{M}^{(n)}(\boldsymbol{k})e^{i\sum _{j}k_{j}\theta _{j}m_{j}}, \end{aligned}\)

(28)

where the Fourier observable simulates all possible correlations generated in an experimental network and is defined as

\(\begin{aligned} \mathcal {\tilde{G}}_{\boldsymbol{S}}^{(n)}\left( \boldsymbol{k}\right) =\left\langle \prod _{j=1}^{d}\bigotimes _{i\in S_{j}}\left( \pi _{i}(0)+\pi _{i}(1)e^{-ik_{j}\theta _{j}}\right) \right\rangle _{P}. \end{aligned}\)

(29)

Here, \(\theta _{j}=2\pi /(M_{j}+1)\), \(k_{j}=0,\dots ,M_{j}\) and \(\pi _{j}=\textrm{exp}(-n'_{j})(\textrm{exp}(n'_{j})-1)^{c_{j}}\) is the positive-P click observable, obtained from the equivalence Eq. (20), where \(n'_{j}=\alpha '_{j}\beta '_{j}\) is the output photon number.

This simulation method is highly scalable, with observables such as \(d=1,2\) dimensional GCPs, first and second-order marginals taking a few minutes to simulate on a desktop computer for current experimental scales. This scalability is highlighted by simulations of total counts for much larger network sizes of up to \(M=16,000\) modes [30], which is much larger than the current generation of GBS networks. We note however that increasing the GCP dimension to \(d\ge 4\) causes the simulations to take hours as opposed to minutes. This is not particularly limiting for current experimental networks, since \(d=4\) is also the experimental data limit, where the increase in sampling errors from too few counts per bin reduces the accuracy of statistical tests [32].

5.2 Phase-space classical sampler

If classical states are input into a GBS, the network can be efficiently simulated using the diagonal P-representation, which arises as a special case of the positive P-representation if \(P(\boldsymbol{\alpha },\boldsymbol{\beta })=P(\boldsymbol{\alpha })\delta (\boldsymbol{\alpha }^{*}-\boldsymbol{\beta })\). Due to this, initial stochastic samples are still generated using Eq. (26), except now one has rotated to a classical phase-space with \(\boldsymbol{\beta }=\boldsymbol{\alpha }^{*}\).

Similar to non-classical states, the input density matrix for any classical state is defined as

\(\begin{aligned} \hat{\rho }^{(\text {in})}=\int P(\boldsymbol{\alpha })\left| \boldsymbol{\alpha }\right\rangle \left\langle \boldsymbol{\alpha }\right| \text {d}^{2}\boldsymbol{\alpha }, \end{aligned}\)

(30)

where the form of the distribution \(P(\boldsymbol{\alpha })\) changes depending on the state. Input amplitudes are again transformed to outputs following \(\boldsymbol{\alpha }'=\boldsymbol{T}\boldsymbol{\alpha }\) or \(\boldsymbol{\alpha }'=\boldsymbol{T}\boldsymbol{B}\boldsymbol{\alpha }\) for single or two-mode states, respectively, and are used to define the output state

\(\begin{aligned} \hat{\rho }^{(\text {out})}=\int P(\boldsymbol{\alpha })\left| \boldsymbol{\alpha }'\right\rangle \left\langle \boldsymbol{\alpha }'\right| \text {d}^{2}\boldsymbol{\alpha }. \end{aligned}\)

(31)

Using the output coherent amplitudes, one can now efficiently generate binary patterns corresponding to any classical state input into a linear network. In order to conserve the simulated counts for each ensemble, corresponding to a single experimental shot, the jth output mode of the kth ensemble is independently and randomly sampled via the Bernoulli distribution [32]

\(\begin{aligned} P_{j}^{(k)}\left(c_{j}^{(\text {class)}}\right)=\left(p_{j}^{(k)}\right)^{c_{j}^{(\text {class)}}}\left(1-p_{j}^{(k)}\right)^{1-c_{j}^{(\text {class)}}}. \end{aligned}\)

(32)

Here, \(c_{j}^{(\text {class})}=0,1\) is the classically generated bit of the jth mode where the probability of \(c_{j}^{(\text {class})}=1\), the “success” probability, is

\(\begin{aligned} p_{j}^{(k)}=(\pi _{j}(1))^{(k)}=\left( 1-e^{-n'_{j}}\right) ^{(k)}. \end{aligned}\)

(33)

This is simply the click probability of the kth stochastic ensemble with an output photon number of \(n'_{j}=\left| \alpha _{j}\right| ^{2}\).

For an M-mode network, each stochastic ensemble outputs a classical faked pattern of the form

\(\begin{aligned} (\boldsymbol{c}^{(\text {class})})^{(k)}=[P_{1}^{(k)},P_{2}^{(k)},\dots ,P_{M}^{(k)}], \end{aligned}\)

(34)

which are binned to obtain GCPs, denoted \(\mathcal {G}^{(\text {class})}\), that can be compared to simulated distributions.

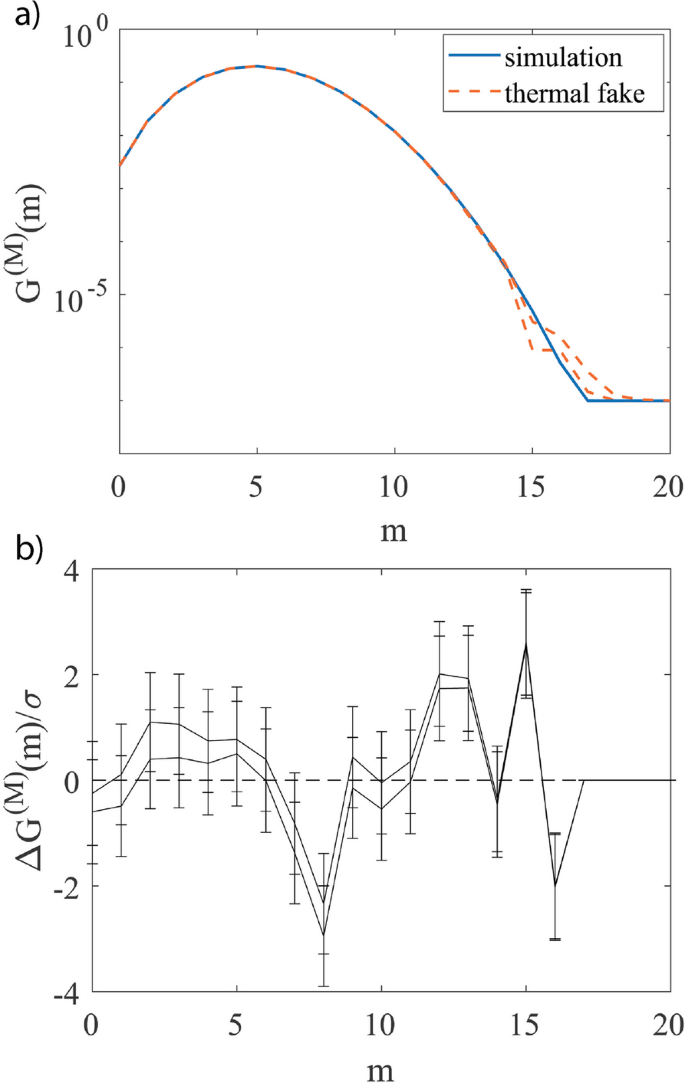
In the limit of large numbers of patterns, binned classical fakes are approximately equal to the simulated output distribution corresponding to the density matrix Eq. (31). An example of this can be seen in Fig. 3 where \(4\times 10^{6}\) binary patterns are generated by sending \(N=20\) thermal states into an \(M=N\) mode lossless linear network represented by a Haar random unitary. The binned classical patterns produce a total count distribution that agrees with simulations within sampling error, because for this classical input example, there is no quantum advantage.

Comparisons of total counts, the m count probability regardless of pattern, for \(4\times 10^{6}\) classical binary patterns generated from thermal states with \(\boldsymbol{r}=[1,\dots ,1]\) input into a \(20\times 20\) Haar random unitary matrix \(\boldsymbol{U}\) with transmission coefficient \(t=0.5\). a Positive-P phase-space simulated output distribution, obtained using \(E_{S}=1.2\times 10^{6}\) ensembles, for thermal states sent into a linear network denoted by the solid blue line are compared against the distribution produced by the binned thermal fake patterns which are represented by the orange dashed line. b Comparison of the normalized difference \(\Delta \mathcal {G}^{(M)}(\boldsymbol{m})/\sigma _{m}=\left( \bar{\mathcal {G}}-\mathcal {G}^{\text {(class)}}\right) /\sigma _{m}\), where \(\sigma _{m}\) is the sum over compared grouped count variances (following from Eq. (35)), and \(\mathcal {G}^{\text {(class)}}\) represents a classically simulated, discrete count probability. Upper and lower lines correspond to one standard deviation of theoretical phase-space sampling errors, while the error bars correspond to the sampling errors of the simulated “fake” counts. The results are cut off for photon count bins containing less than 10 counts. The expected good agreement becomes clearer when Z-score statistical tests are performed, giving \(Z^{(\text {class})}\approx 1\). In this example, since the input is classical there is no quantum advantage, and the classical sampler is exact, as expected

 Full size image 

5.3 Statistical tests

For comparisons to be meaningful, statistical tests are needed to quantify differences between experiment and theory. To this end, Refs. [30, 31] implement a slightly altered version of a standard chi-square test, which is frequently used in random number generator validation [109, 110], and is defined as

\(\begin{aligned} \chi _{ES}^{2}=\sum \limits _{i=1}^{k}\frac{\left( \mathcal {G}_{i,E}-\bar{\mathcal {G}}_{i,S}\right) ^{2}}{\sigma _{i}^{2}}. \end{aligned}\)

(35)

Here, k is the number of valid photon count bins, which we define as a bin with more than 10 counts, and \(\mathcal {\bar{G}}_{i,S}\) is the phase-space simulated GCP ensemble mean for any input state S, which converges to the true theoretical GCP, \(\mathcal {G}_{i,S}\), in the limit \(E_{S}\rightarrow \infty\). The experimental GCP is defined as \(\mathcal {G}_{i,E}\), and \(\sigma _{i}^{2}=\sigma _{T,i}^{2}+\sigma _{E,i}^{2}\) is the sum of experimental, \(\sigma _{E,i}^{2}\), and theoretical, \(\sigma _{T,i}^{2}\), sampling errors of the i-th bin.

The chi-square test result follows a chi-square distribution that converges to a normal distribution when \(k\rightarrow \infty\) due to the central limit theorem [111, 112]. One can use this to introduce another test that determines how many standard deviations away the comparison result is from its expected normally distributed mean. The aim of this test is to obtain the probability of observing the output \(\chi _{ES}^{2}\) result using standard probability theory. For example, an output of \(6\sigma\), where \(\sigma\) is the standard deviation of the normal distribution, indicates the data has a very small probability of being observed.

To do this, Ref. [32] implemented the Z-score, or Z-statistic, test which is defined as

\(\begin{aligned} Z_{ES}=\frac{\left( \chi _{ES}^{2}/k\right) ^{1/3}-\left( 1-2/(9k)\right) }{\sqrt{2/(9k)}}, \end{aligned}\)

(36)

where \(\left( \chi _{ES}^{2}/k\right) ^{1/3}\) is the Wilson-Hilferty (WH) transformed chi-square statistic [111], which allows a faster convergence to a normal distribution when \(k\ge 10\) [111, 112], and \(\mu =1-\sigma ^{2}\), \(\sigma ^{2}=2/(9k)\) are the corresponding mean and variance of the normal distribution.

The Z-statistic allows one to determine the probability obtaining the resulting \(\chi ^{2}/k\) value. A result of \(Z_{ES}>6\) would indicate that experimental distributions are so far from the simulated results that patterns may be displaying systematic errors. Valid experimental results with correct distributions should have \(\chi _{EI}^{2}/k\approx 1\), where the subscript I denotes the ideal GBS distribution, with \(Z_{EI}\approx 1\). For claims of quantum advantage, one must simultaneously prove that \(Z_{CI}\gg 1\), where the subscript C denotes binary patterns from the best classical fake, such as the diagonal-P method described above. This is the ’gold standard’ and would show that, within sampling errors, experimental samples are valid, and closer to the ideal distribution than any classical fake.

In the more realistic scenario of thermalized squeezed inputs, one may still have quantum advantage if \(Z_{ET}\approx 1\) while \(Z_{CT}\gg 1\), where the T indicates a simulated thermalised squeezed state. Therefore, these four observables are of the most interest for comparisons of theory and experiment, and are given below.

5.4 Comparisons with experiment

Throughout this section, for purposes of illustration, we primarily review comparisons of data from Jiuzhang 1.0 using two-mode squeezed state inputs. A thorough comparison of all data sets obtained in Jiuzhang 2.0 is presented elsewhere [32].

We first review comparisons of total counts, which is the probability of observing m clicks in any pattern and is usually one of the first observables experimentalists compare samples to. This is because in the limit of a large number of clicks, one can estimate the ideal distribution as a Gaussian distribution via the central limit theorem.

To simulate the ideal total counts distribution in phase-space using GCPs we let \(n=M\) and \(\boldsymbol{S}=\{1,2,\dots ,M\}\), giving \(\mathcal {G}_{\{1,\dots ,M\}}^{(M)}(m)\). For Jiuzhang 1.0, one obtains a Z-statistic of \(Z_{EI}\approx 408\) for \(k=61\) valid bins. Clearly, experimental samples are far from the ideal and indicate photon count distributions are not what would be expected from an ideal GBS.

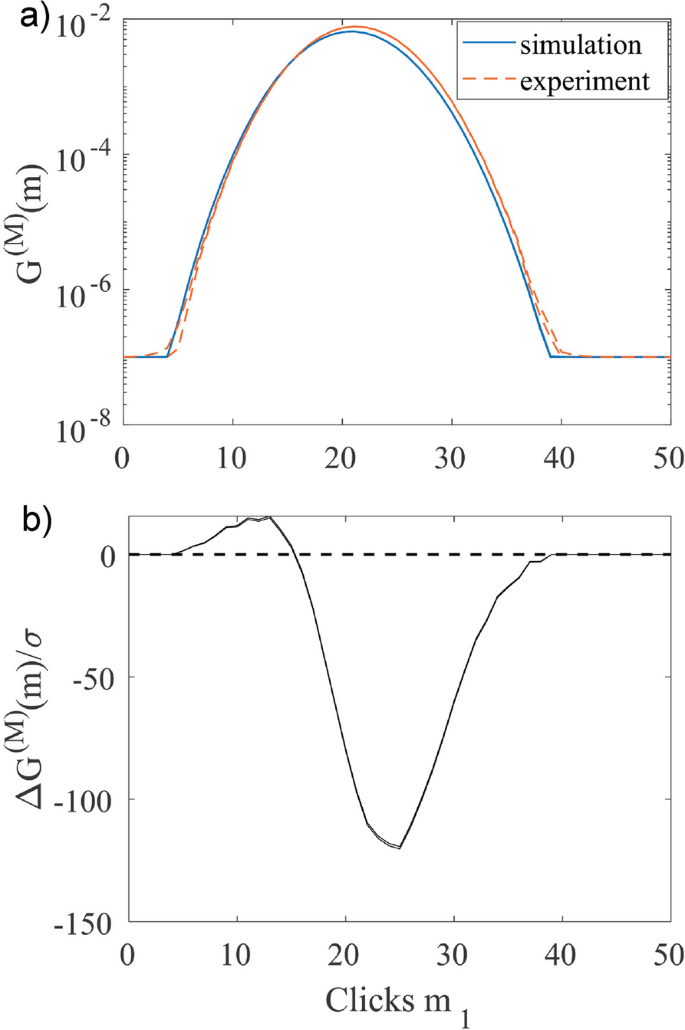
a Comparison of a one-dimensional planar slice through the maximum of a \(d=2\) dimensional GCP \(\mathcal {G}_{50,50}^{(100)}(m)\) for binary patterns from Jiuzhang 1.0 data (dashed orange line). Phase-space simulations (solid blue line) are performed for the ideal GBS, without decoherence, and use \(E_{S}=1.2\times 10^{6}\) stochastic ensembles. b Normalized difference between theory and experiment \(\Delta \mathcal {G}^{(M)}(\boldsymbol{m})/\sigma _{m}\) versus \(m_{1}\), which is the grouped count for modes contained within the first subset \(S_{1}\). Upper and lower solid black lines are \(\pm 1\sigma _{T}\), with grouped count bins containing less than 10 counts being cut off. Although the distributions are visually similar in a), the normalized difference shows that significant discrepancies are present (see Fig. 3 for definitions), and one can readily determine that the ideal GBS model is not validated for this set of experimental data, although the agreement is much better if a decoherent, thermalized model is used instead

 Full size image 

To determine whether these differences either increase or decrease when higher-order correlations become more prevalent in the simulations, the dimension of the GCP is increased to \(d=2\). In this case, Jiuzhang 1.0 sees an almost doubling in Z values for comparisons with the simulated ideal distribution (see Fig. 4), where \(Z_{EI}\approx 796\) is obtained from \(k=975\) [30]. The increase in the number of valid bins with GCP dimension causes the normal distribution of the WH transformed chi-square statistic to have a smaller variance. When compared to a single dimension, where \(k=61\) gives \(\sigma ^{2}\approx 3.6\times 10^{-3}\), binning with \(d>1\) causes experimental samples to now pass a more stringent test, as \(k=975\) produces a normal distribution with variance \(\sigma ^{2}\approx 2.3\times 10^{-4}\).

Simulating the more realistic scenario of thermalized squeezed states, a thermalized component of \(\epsilon =0.0811\pm 0.0005\) and a transmission matrix correction of \(t=1.0305\pm 0.0005\) is used as to compare a simulated model to samples from Jiuzhang 1.0. This is very close to the original, modified parameters [30]. In this case, an order of magnitude improvement in the resulting Z value is observed, giving \(Z_{ET}\approx 17\pm 2\) for total counts.

Despite this significant improvement, differences are still large enough that \(Z_{ET}>1\). Similar results were also obtained for data sets with the largest recorded photon counts in Jiuzhang 2.0, that is data sets claiming quantum advantage [32]. However, this is not the case for data sets with small numbers of recorded photons which typically give \(Z_{ET}\approx 1\) [32], although these experiments should be easily replicated by exact samplers. The large amount of apparent thermalization is the likely reason why simulated squashed states described Jiuzhang 1.0 samples just as well as the ideal GBS in Ref. [89].

When higher-order correlations are considered, samples from Jiuzhang 1.0 are far from the expected correlation moments of the ideal distribution. Although including the above fitting parameters improves this result with \(Z_{ET}\approx 130\) for d=2, the samples still deviate significantly from the theoretical thermalized distribution [30].

Unlike comparisons of total counts, samples from all data sets in Jiuzhang 2.0 satisfy \(Z_{EI},Z_{ET}>1\) for simulations with \(d>1\), meaning higher-order correlations also display significant departures from the expected theoretical results, even for the simpler cases with low numbers of photon counts [32]. The reasons for this are not currently known.

In order to effectively validate GBS quantum computers, scalable methods are needed which capture the entire interference complexity of linear networks. The positive-P phase-space representation is the only currently known method which can simulate every measurable grouped output distribution with non-classical input states, allowing efficient comparisons of theory and experiment for data that is available on a reasonable time-scale. Although it is currently limited to GBS with click detectors, an extension to GBS with PNR detectors is possible since the positive-P representation is still useful, although a different binning method is required since the outputs are no longer binary.

One of the important issues here is the extraordinary relative sparseness of the experimental data, which makes it completely impossible to experimentally recover any reasonable estimate of the full distribution. Thus, while the full distribution is exponentially hard to compute, it is equally hard to measure. This means that comparisons of theory and experiment always involve some type of grouping or binning of the available data.

The next significant point is that one can both experimentally measure and theoretically compute the grouped distributions. This can be carried out theoretically with great precision using the positive-P phase-space simulation method, combined with a Fourier transform binning algorithm. These do not add greatly to the computational overhead, giving exact tests that are computable in just a few minutes, which is of great practical value.

The resulting statistical tests employed in these comparisons are far more scalable than ones implemented in many previous comparisons [15,16,17,18, 23,24,25], as they do not require the computation of photon count pattern probabilities, which limits the comparisons that can be performed using these tests. Exact simulation using direct photon counts is impractical in the large-scale regime where quantum advantage is found.

Statistical testing shows that the GBS experiments tested are far from the ideal GBS output distributions which are obtained from injecting pure squeezed vacuum states into a linear network. The reason for the discrepancy is that some form of decoherence is inevitable in such large quantum systems, and this makes the ideal standard too high a bar that is unlikely to ever be fully realized. A more reasonable goal is an output distribution obtained from including some decoherence in the inputs, although the amount of decoherence must be small enough that input states remain non-classical.

In summary, the positive P-representation provides an effective, scalable method to validate quantum photonic network data. It is not limited to quantum computing applications such as the GBS, as the theory presented here can be readily adapted to other optical networks, and can include non-ideal features that occur in practical experiments. Having a target distribution which is non-ideal yet non-classical is the “Goldilocks” target calculation of these devices: a porridge which is neither too hot nor too cold.