Abstract
Hard exclusive reactions initiated by pion or photon beams within the near-backward kinematical regime specified by the small Mandelstam variable \(-u\) can be studied to access pion-to-nucleon and photon-to-nucleon transition distribution amplitudes (TDAs). Checking the validity of collinear factorized description of pion and photon induced reactions in terms of TDAs allows to test the universality of TDAs between the space-like and time-like regimes that is the indispensable feature of the QCD collinear factorization approach.
In this short review, we consider the exclusive pion- and photo-production off nucleon of a highly virtual lepton pair (or heavy quarkonium) in the near-backward region. We first employ a simplistic cross channel nucleon exchange model of pion-to-nucleon TDAs to estimate the magnitude of the corresponding cross sections for the kinematical conditions of J-PARC. We then illustrate the flexibility of our approach by building a two parameter model for the photon-to-nucleon TDAs based on recent results for near threshold \(J/\psi\) photoproduction at JLab and provide our estimates for near-backward \(J/\psi\) photoproduction and timelike Compton scattering cross sections for the kinematical conditions of JLab and of future EIC and EIcC.
1 Introduction
Complementary to deep electroproduction reactions such as the much studied near-forward deeply virtual Compton scattering (DVCS) and deeply virtual meson production (DVMP), the validity of the collinear factorization approach for hard exclusive reactions and the relevance of the leading twist approximation analysis can be challenged in studies of time-like reactions such as near-forward photoproduction of lepton pairs [1, 2] and the exclusive limit of the Drell-Yan process in \(\pi\) beam experiments [3, 4]. Analyticity (in \(Q^2\)) properties of the leading twist scattering amplitudes [5] exressed within the collinear factorization framework in terms of generalized parton distribution (GPDs) and meson distribution amplitudes (DAs) relate these time-like and space-like reactions.
The first experimental study of timelike Compton scattering (TCS) performed at JLab was recently reported by the CLAS collaboration [6]. The new results for \(J/\psi\) photoproduction reactions near threshold [7] attracted much attention in the context of the studies of GPDs (see [8] for a review) and the energy momentum tensor of the nucleon [9].
A natural extension of this research program is the study of the crossed (\(t \leftrightarrow u\)) channel counterpart reactions, i.e. the same hard exclusive reactions in the near-backward kinematics, admitting a description in terms of meson-to-nucleon [10] or photon-to-nucleon [11] transition distribution amplitudes (TDAs). Nucleon-to-meson (and nucleon-to-photon) TDAs, as well as their crossed version, are defined as transition matrix elements between a nucleon and a meson (or a photon) states of the same non-local three-quark operator on the light-cone occurring in the definition of baryon DAs (see Ref. [12] for a review). They arise within the collinear factorization framework for hard exclusive electroproduction reactions in near-backward kinematics [13].
The physical contents of nucleon-to-meson and nucleon-to-photon TDAs is conceptually similar to that of GPDs enriched by the three-quark structure of the QCD operator which defines them. Since this operator carries the quantum numbers of baryons, it provides access to the momentum distribution of baryonic number inside hadrons. It intrinsically gives access to the non-minimal Fock components of hadronic light-front wave functions. Similarly to GPDs, by switching to the impact parameter space, one can address the distribution of the baryonic charge inside hadrons in the transverse plane. This also enables to study the mesonic and electromagnetic clouds surrounding hadrons and provides new tools for microsurgery and femtophotography of hadrons.
In this paper, we focus on the photon or pion beam induced hard exclusive reactions, being motivated by the intensive experimental studies at JLab [13, 14] and prospects to access backward hard exclusive reactions at J-PARC [15] and future EIC [16, 17] and EIcC [18]. Also, recent measurements of the \(J/\psi\) photoproduction cross section over the full near-threshold kinematic region [19] provide some more hints in favor of the manifestation of a backward peak in exclusive cross sections.
We review the existing results for near-backward TCS [11] and pion-beam-induced near-backward \(J/\psi\) production [10] and present new cross section estimates for near-backward \(J/\psi\) photoproduction process and pion beam induced near-backward production of lepton pairs.
2 Kinematics of pion and photon beam initiated backward reactions
In this section, we consider the near-backward kinematics regime for hard processes
where \(s_N\), \(s'_N\) (\(\lambda _\gamma\), \(\lambda '_\gamma\), \(\lambda _\psi\)) stand for nucleon (photon or charmonium) polarization variables.
For definiteness, we choose to present the necessary formulas for
-
The expressions for the case of the photoproduction reactions can be obtained with the obvious change
\(\begin{aligned} p_\pi \rightarrow q; \ \ \ p_\pi ^2= m_\pi ^2 \rightarrow q^2=0. \end{aligned}\)(3)
-
The set of kinematical formulas when the final state virtual photon \(\gamma ^*(q', \lambda '_\gamma )\) is replaced by the heavy quarkonium \(J/\psi (p_\psi , \lambda _\psi )\) can be obtained by changing
\(\begin{aligned} q' \rightarrow p_\psi ; \ \ \ {q'}^2=Q'^2 \rightarrow p_\psi ^2= {M_\psi ^2}. \end{aligned}\)(4)
To describe the \(2 \rightarrow 2\) hard subprocess (2), we employ the standard Mandelstam variables
with \(s+t+u=2m_N^2 +m_\pi ^2+Q'^2\). The z-axis is chosen along the direction of the pion beam in the meson-nucleon center-of-momentum (CMS) frame. We introduce the light-cone vectors p, n (\(p^2=n^2=0\)) satisfying \(2p \cdot n =1\). The Sudakov decomposition of the relevant momenta reads
where
is the Mandelstam function and \(m_N\) and \(m_\pi\) stand respectively for the nucleon and pion masses. The transverse direction in (6) is defined with respect to the z direction and \(\xi\) is the skewness variable that specifies the longitudinal momentum transfer in the u-channel:
The transverse invariant momentum transfer \(\Delta _T^2 \le 0\) is expressed as
Within the collinear factorization framework, we neglect both the pion and nucleon masses with respect to the hard scale introduced by \(Q'\) (or \(M_\psi\)) and W and set \(\Delta _T=0\) within the coefficient functions. This results in the approximate expression for the skewness variable (8):
where \(\tau\) is the time-like analog of the Bjorken variable
It is also instructive to consider the exact kinematics of the reaction (2) in the \(\pi N\) CMS frame. In this frame the relevant momenta read:
where
The CMS scattering angle \(\theta _u^*\) is defined as the angle between \(\textbf{p}_\pi\) and \(\textbf{p}'_N\):
The transverse momentum transfer squared (9) is then given by
and the physical domain for the reaction (2) is defined from the requirement that \(\Delta _T^2 \le 0\).
-
In particular, the backward kinematics regime \(\theta _u^*=0\) corresponds to \(\textbf{p}'_N\) along \(\textbf{p}_\pi\), which means that \(\gamma ^*\) is produced along \(-\textbf{p}_\pi\), i.e. in the backward direction. In this case, u reaches its maximal value
\(\begin{aligned}{} & {} u_{0} \equiv \frac{2 \xi (m_\pi ^2(\xi -1)+m_N^2(\xi +1))}{\xi ^2-1}\nonumber \\{} & {} =m_N^2+m_\pi ^2- \frac{(W^2+m_\pi ^2-m_N^2)(W^2+m_N^2-Q'^2)}{2W^2} + 2|\textbf{p}_\pi ||\textbf{q}'|. \end{aligned}\)(16)
At the same time, \(t=(p'_N-p_N)^2\) reaches its minimal value \(t_{1}\) (\(W^2+u_{0}+t_{1}=2m_N^2+m_\pi ^2+Q'^2\)). Note that u is negative, and therefore \(|u_{0}|\) is the minimal possible absolute value of the momentum transfer squared. It is for \(u \sim u_{0}\) that one may expect to satisfy the requirement \(|u| \ll W^2, \, Q'^2\) which is crucial for the validity of the factorized description of (2) in terms of \(\pi \rightarrow N\) TDAs and nucleon DAs.
-
Another limiting value \(\theta _u^*=\pi\) corresponds to \(\textbf{p}'_N\) along \(-\textbf{p}_\pi\) i.e \(\gamma ^*(q')\) produced in the forward direction. In this case u reaches its minimal value
\(\begin{aligned} u_{1}=m_N^2+m_\pi ^2- \frac{(W^2+m_\pi ^2-m_N^2)(W^2+m_N^2-Q'^2)}{2W^2} - 2|\textbf{p}_\pi ||\textbf{q}'|. \end{aligned}\)(17)
At the same time, t reaches its maximal value \(t_{0}\). The factorized description in terms of \(\pi \rightarrow N\) TDAs does not apply in this case as |u| turns out to be of order of \(W^2\).
3 Pion-to-nucleon and photon-to-nucleon TDAs
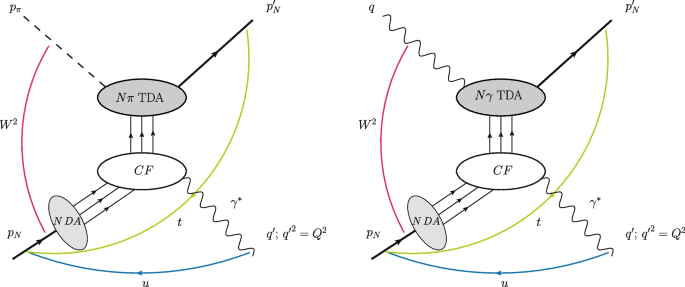
In Figs. 1 and 2 we present the hard scattering mechanisms for the near-backward kinematical regime for hard reactions (1) (see Section 2) involving pion-to-nucleon (\(N \pi\)), respectively photon-to-nucleon (\(N \gamma\)), TDAs and nucleon DAs.
\(N \pi\) and \(N \gamma\) TDAs are defined as Fourier transforms of matrix elements of non-local three-antiquark light-cone operator between a pion (or a photon) state and a nucleon state. For definiteness, we consider \(\pi ^- \rightarrow n\) and \(\gamma \rightarrow p\) \(\bar{u} \bar{u} \bar{d}\) TDAs defined with the trilocal light-cone operatorFootnote 1
Here, \(c_{1,2,3}\) stand for the color group indices and \(\rho\), \(\tau\), \(\chi\) denote the Dirac indices. Other isospin channels can be worked out with help of the isospin symmetry relations worked out in Ref. [20].
Collinear factorization mechanism for the hard subprocess of near-backward lepton pair production induced by pion beam \(\pi N \rightarrow N' \gamma ^*\) (left panel) and backward TCS \(\gamma N \rightarrow N' \gamma ^*\) (right panel); large scale is provided by \(Q'^2\) and \(W^2 \equiv (p_N+q)^2\); fixed \(\tau\) (11); \(|u|\equiv |(p_N-q')^2| \sim 0\)); \(N\pi\) (\(N\gamma\)) TDA stands for the transition distribution amplitudes from a pion-to-nucleon (photon-to-nucleon); N DA stands for the nucleon distribution amplitude. CF denotes the coefficient function (hard convolution kernel)
Collinear factorization mechanism of charmonium photoproduction (\(\gamma N \rightarrow J/\psi N'\)) in the near-backward kinematical regime (large scale is provided by \(M_\psi ^2\) and \(W^2 \equiv (p_N+q)^2\); fixed \(\tau\) (11); \(|u|\equiv |(p'_N-q)^2| \sim 0\)); \(N\gamma\) TDA stands for the transition distribution amplitudes from a photon-to-a-nucleon; N DA stands for the nucleon distribution amplitude. Black dots denote the non-relativistic light-cone wave function of heavy quarkoinum (35)
The number of leading twist TDAs matches the number of independent helicity amplitudes \(T_{h_{\bar{u}} h_{\bar{u}},h_{\bar{d}}}^{ h_N }\) and \(T_{h_{\bar{u}} h_{\bar{u}},h_{\bar{d}}}^{ h_\gamma , h_N }\) for \(\pi \, u u d \rightarrow N^p\) and \(\gamma \, u u d \rightarrow N^p\) process, where \(h_{\bar{q}}\), \(h_\gamma\), and \(h_N\) refer to the light-cone helicity of, respectively, quark, initial state photon and the final state nucleon.
To the leading twist-3 accuracy, the parametrization of pion-to-nucleon TDAs involves 8 independent \(N \pi\) TDAs
where the Fourier transform operation is defined as \(4 \mathcal {F} \equiv 4(p \cdot n)^{3} \int \left[ \prod _{j=1}^{3} \frac{d \lambda _{j}}{2 \pi }\right] e^{-i \sum _{k=1}^{3} x_{k} \lambda _{k}(p \cdot n)}\); \(f_N=5.0 \times 10^{-3}\) GeV\(^2\) is the nucleon light-cone wave function normalization constant [21]; and \(f_\pi =93~{\text {MeV}}\) is the pion weak decay constant. The explicit expressions for the Dirac structures \(\{v^{N \pi },\,a^{N \pi },\, t^{N \pi } \}\) are presented in Appendix A. Each of TDAs is a function of three momentum fraction variables \(x_i\); skewness variable \(\xi\) (8), u-channel invariant momentum transfer \(\Delta ^2\), and of the factorization scale \(\mu ^2\).
The parametrization of photon-to-nucleon TDAs involves 16 independent \(N \gamma\) TDAs \(V_{\Upsilon }^{N \gamma }, \, A_{\Upsilon }^{N \gamma }, \, T_{\Upsilon }^{N \gamma }\):
The crossing relations expressing pion-to-nucleon and photon-to-nucleon through nucleon-to-pion and nucleon-to-photon TDAs occurring in the description of electroproduction reactions are summarized in Appendix A. We refer the reader to Section 4 of the review paper [12] for a detailed overview of symmetry, support and evolution properties of TDAs and their physical contents and interpretation.
4 Amplitudes and cross sections of pion beam induced reactions
In this section, we present a set of formulas for pion beam induced near-backward production of a highly virtual lepton pair (or of heavy quarkonium). For this issue, we consider the hard subprocesses
Within the u-channel factorized description in terms of \(N \pi\) TDAs (and nucleon DAs) to the leading order in \(\alpha _s\), the amplitude of the hard \(\pi N \rightarrow N' \gamma ^{*}\) subprocess \(\mathcal {M}^{\lambda '_\gamma }_{s_N s'_N}\) is expressed as
with the overall normalization constant \(\mathcal {C}_\pi\)
where \(\alpha _{em} = \frac{e^2}{4 \pi } \simeq \frac{1}{137}\) is the electromagnetic fine structure constant, \(\alpha _s \simeq 0.3\) is the strong coupling.
The spin structures \(\mathcal {S}^{(k) \, \lambda '_\gamma }_{s_N s'_N}\), \(k=1,\,2\) are defined as
where \({\mathcal {E}}_\gamma (q,\lambda _\gamma )\) stands for the polarization vector of the virtual photon; U are the nucleon Dirac spinors; and the standard Dirac’s “hat” notations are adopted. \(\mathcal {J}^{(k)}_{\pi N \rightarrow N' \gamma ^*}\) \(k=1,2\) denote the convolution integrals of \(\pi N\) TDAs and antinucleon DAs with the hard scattering kernels computed from the set of 21 relevant scattering diagrams (see [22]):
The integrals in \(x_i\)’s (\(y_i\)’s) in (24) stand over the support of \(N \pi\) TDA (nucleon DA). Within the u-channel factorization regime of \(\pi N \rightarrow N' \gamma ^*\), the coefficients \(R_\alpha ^{(k)}\) (\(\alpha =1,\ldots ,14\)) correspond to the coefficients \(T_\alpha ^{(k)}=D_\alpha \times N_\alpha ^{(k)}\) that can be read off from Table 2 of Ref. [12], with the replacement of nucleon-to-pion (\(\pi N\)) TDAs by pion-to-nucleon (\(N \pi\)) TDAs multiplied by an irrelevant charge conjugation phase factor and with the modification \(-i 0 \rightarrow i 0\) of the regulating prescription in the denominators of hard scattering kernels \(D_\alpha\). The latter changes mirror the difference between the electroproduction hard exclusive reactions with spacelike \(\gamma ^*\) and pion-production hard exclusive reactions in which \(\gamma ^*\) is timelike.
Now, the cross section of the near-backward lepton pair production reaction
can be expressed as
where \(d\Omega ^{*}_{N'} \equiv d \cos \theta _{N'}^{*} d \varphi _{N'}^{*}\) is the final nucleon solid angle in the \(\pi N\) CMS. By \(d \Omega _\ell \equiv d \cos \theta _\ell d \varphi _\ell\), we denote the produced lepton solid angle in \(\ell ^+ \ell ^-\) CMS (corresponding to the rest frame of the virtual photon). By expressing \(\cos \theta _{N'}^{*}\) through \(u = (p'_{N}-p_\pi )^2\) as
and integrating over the azimuthal angle \(\varphi _{N'}^{*}\) of the produced nucleon and over the azimuthal angle of the lepton \(\varphi _\ell\) the following formula for the unpolarized differential cross section of the reaction (25) is established:
The average-squared amplitude \(| \overline{\mathcal {M}_{ \pi N \rightarrow N' \ell ^+ \ell ^- }}| ^2\) is expressed through the helicity amplitudes of the hard subprocess \(\mathcal {M}^{\lambda '_\gamma }_{s_N s'_{{N}}}(\pi N \rightarrow N' \gamma ^*)\) (21)
where the factor \(\frac{1}{2}\) corresponds to averaging over polarization of the initial state nucleon.
Within the factorized description in terms of \(N\pi\) TDAs (and nucleon DAs) to the leading twist accuracy, only the contribution of transverse polarization of the virtual photon is relevant. By computing the leptonic trace in (29) in the \(\ell ^+ \ell ^-\) CMS, and integrating over the lepton polar angle \(\varphi _\ell\), we obtain:
where
Here, \(\mathcal {J}^{(1,2)}\) are the integral convolutions defined in (24) and \(\mathcal {C}_\pi\) is the overall normalization constant (22).
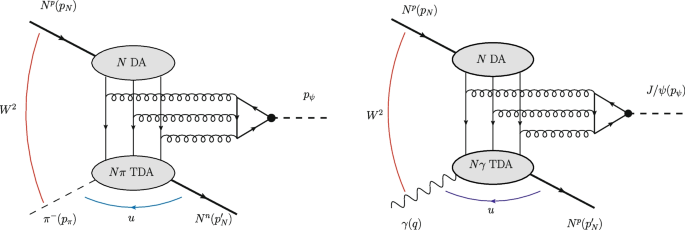
Now, following Ref. [10], we review the basic amplitude and cross section formulas for near-backward charmonium production in \(\pi N\) collisions within the TDA framework assuming the collinear factorization reaction mechanism depicted in the left panel of Fig. 2. The leading order and leading twist amplitude \(\mathcal {M}^{\lambda _\psi }_{s_N s'_N}\) of the hard reaction \(\pi N \rightarrow N' J/\psi\) admits the following parametrization
where the average mass \(\bar{M}\) approximately equals the charmonium mass that is roughly twice the mass of the charmed quark:
The spin structures \(\mathcal {S}^{(k) \, \lambda _\psi }_{s_N s'_N}\), \(k=1,\,2\) occurring in (32) are the same as in Eq. (23) with the virtual photon polarization vector \({\mathcal {E}}^{*}_\gamma (q', \lambda '_\gamma )\) replaced by the charmonium polarization vector \({\mathcal {E}}^{*}_\psi (p_\psi , \lambda _\psi )\). The explicit expressions for the convolution integrals \(\mathcal {J}^{(1,2)}_{\pi N \rightarrow N' J/\psi '}(\xi ,\Delta ^2)\) are presented in Appendix B1 The normalization constant \(\mathcal {C}_\pi ^\psi\) reads
where \(f_\psi\) determines the normalization of the non-relativistic light-cone wave function of heavy quarkonium [23]:
The normalization constant \(f_\psi\) can be extracted from the charmonium leptonic decay width \(\Gamma (J/ \psi \rightarrow e^+ e^-)\). With the values quoted in Ref. [24], we get \(f_\psi = 415.5 \pm 4.9\) MeV.
To work out the cross section formula we square the amplitude (32) and average (sum) over spins of initial (final) nucleon. Staying at the leading twist-3 accuracy, we account for the production of transversely polarized \(J/\psi\). Summing over the transverse polarizations, we find
The leading twist-3 differential cross section of \(\pi +N \rightarrow J/\psi + N'\) then reads
where \(\xi\) is the u-channel skewness variable (8)
and \(\Lambda (x,y,z)\) is defined in (7).
5 Amplitude and cross sections of photoproduction reactions
In this section, we review the near-backward photoproduction off nucleon of a highly virtual lepton pair or of heavy quarkonium. The hard subprocesses of these two reactions
are considered within the collinear factorization framework. The corresponding hard scattering mechanisms are depicted in the right panels of Figs. 1 and 2 respectively.
For the backward timelike Compton scattering (TCS) reaction
we closely follow the exposition of Ref. [11]. The helicity amplitudes \(\mathcal {M}^{\lambda _\gamma \lambda '_\gamma }_{s_N s'_N}\) of (40) involve 4 independent tensor structuresFootnote 2
with the overall normalization constant \(\mathcal {C}_V\)
There is one tensor structure independent of \(\Delta _T\):
and three \(\Delta _T\)-dependent tensor structures:
The explicit expressions for the convolution integrals \(\mathcal {J}_{ \gamma N \rightarrow N' \gamma ^* }^{(k)} (\xi , \, \Delta ^2)\) can be read off from the expressions for the set of 21 relevant scattering diagrams summarized in Table 1 of [11].
The cross section of the near-backward lepton pair production reaction
integrated over the final nucleon azimuthal angle \(\varphi _{N'}^*\) and lepton azimuthal angle \(\varphi _\ell\) reads
with the average-squared amplitude \(\overline{|\mathcal {M}_{ \gamma N \rightarrow N' \ell ^+ \ell ^-}|^2}\) expressed as
To the leading twist-3 accuracy, the averaged-squared amplitude (47) integrated over the lepton azimuthal angle \(\varphi _\ell\) reads
where
and the \((1 + \cos ^2 \theta _\ell )\) dependence reflects the dominance of transversely polarized virtual photon.
In a similar way, the helicity amplitudes \(\mathcal {M}^{\lambda _\gamma \lambda _\psi }_{s_N s'_N}(\gamma N \rightarrow N' J/\psi )\) of the hard reaction
involve the same 4 independent tensor structures (43), (44) with virtual photon polarization vector \(\mathcal {E}(q', \lambda '_\gamma )\) replaced by that of the heavy quarkonium \(\mathcal {E}(p_\psi , \lambda _\psi )\):
The normalization constant \(\mathcal {C}^\psi _V\) reads
To the leading order in \(\alpha _s\), the hard amplitude of charmonium photoproduction is calculated from the 3 Feynman diagrams analogous to the case of charmonium production with a pion beam. The explicit expressions for the integral convolutions \(\mathcal {J}_{ \gamma N \rightarrow N' J/\psi }^{(k)}\) are presented in Appendix B2. The averaged-squared amplitude (51), to the leading twist-3 accuracy, is expressed as
and the differential cross section of the reaction (50) reads
6 Estimates of pion-beam-induced near-backward lepton pair and charmonium production cross sections
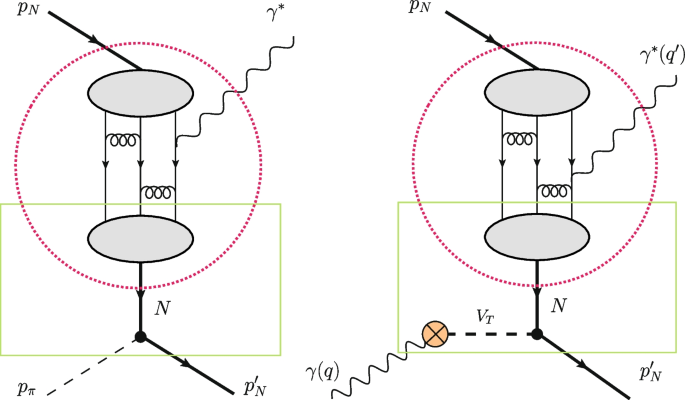
In this section, we present our estimates of pion-beam-induced near-backward lepton pair and charmonium production cross sections for the kinematical conditions of J-PARC within the cross channel nucleon exchange model for \(N \pi\) TDAs (see left panel of Fig. 3). The explicit expressions for nucleon-to-pion (\(\pi N\)) TDAs with the cross channel nucleon exchange model are summarized in Section 5.1 of Ref. [12]. \(N \pi\) TDAs are expressed thorough \(\pi N\) TDAs using the crossing relations (70).
Left panel: Cross channel nucleon exchange amplitude graph for \(\pi N \rightarrow N' \gamma ^*\) in perturbative QCD. Right panel: Cross channel nucleon exchange amplitude graph for \(\gamma N \rightarrow N' \gamma ^*\) within the VMD framework in perturbative QCD; dashed circles contain a typical LO graph for the nucleon electromagnetic form factor in perturbative QCD; the rectangles contain the cross channel nucleon contribution into \(N \pi\) and \(N\gamma\) TDAs. The crossed circle depicts the \(\gamma\) to transversely polarized vector meson vertex
The integral convolutions \(\mathcal {I}^{(k)}_{\, \pi N \rightarrow N'\left\{ \begin{array}{c} \gamma ^*\\ J/\psi \end{array}\right\} }\), \(k=1,\,2\), introduced in Eqs. (21), (32), within the cross channel nucleon exchange model read
Here
-
\(g_{\pi NN} \simeq 13\) stands for the pion-nucleon dimensionless coupling constant;
-
\(\sqrt{2}\) is the isospin factor for the \(\pi ^- p \rightarrow n \left\{ \begin{array}{c} \gamma ^*\\ J/\psi \end{array}\right\}\) channel;
-
\(\mathcal {I}_0\) is the constant occurring in the leading order perturbative QCD description of proton electromagnetic form factor \(F_1^p(Q^2)\) [21]:
\(\begin{aligned} Q^4 F_1^p(Q^2)= \frac{(4 \pi \alpha _s)^2 f_N^2}{54}\mathcal {I}_0. \end{aligned}\)(56)
Thus, the cross section of \(\pi N \rightarrow N' \ell ^+ \ell ^-\) within the cross channel nucleon exchange model for \(N \pi\) TDAs turns out to be proportional to the square of the perturbative QCD nucleon electromagnetic form factor. COZ input nucleon DA [21] provides \(\mathcal {I}_0 \Big |_{\text {COZ}}=1.45 \cdot 10^5\); an input DA with a shape close to the asymptotic form (e.g. Bolz-Kroll [26], Braun-Lenz-Wittmann NLO [27], or that computed from the chiral soliton model [28]) results in a negligibly small value of \(\mathcal {I}_0\) and is thus unable to describe current experimental data on the nucleon electromagnetic form factor staying at the leading twist accuracy. The use of the CZ-type DA solutions can be seen as a way to partially take into account the contribution of the soft spectator mechanism . The regularization of the potential end point singularities then require further theoretical efforts, see e.g. the discussion on the pQCD description of \(\gamma ^* \gamma\) form factors in Ref. [29].
-
\(M_0\) is a well known convolution of nucleon DAs with hard scattering kernel (73) occurring in the \(J/\psi \rightarrow \bar{p} p\) decay amplitude
\(\begin{aligned} \mathcal {M}_{J / \psi \rightarrow \bar{p} p}=\left( 4 \pi \alpha _s\right) ^3 \frac{f_N^2 f_\psi }{\bar{M}^5} \frac{10}{81} \bar{U} \hat{\mathcal {E}}_\psi V M_0. \end{aligned}\)(57)
Therefore, the cross section of near-backward \(J/\psi\) production within the cross channel nucleon exchange model for \(N \pi\) TDAs turns out to be proportional to the \(J/\psi \rightarrow \bar{p} p\) decay width within the pQCD approach [21]:
\(\begin{aligned} \Gamma _{J/\psi \rightarrow p \bar{p}} = (\pi \alpha _s)^6 \frac{1280 f_\psi ^2 f_N^4 }{243 \pi {\bar{M}^9}} |M_0|^2. \end{aligned}\)(58)
For the COZ input nucleon DA, \(M_0 \Big |_{\text {COZ}} \simeq 0.79 \cdot 10^4\). Note a very strong dependence of the decay width on \(\alpha _s\). In the analysis of Ref. [10], the value of \(\alpha _s\) was adjusted to reproduce the experimental value \(\Gamma _{J/\psi \rightarrow p \bar{p}}\) for a given input nucleon DA. In this paper we keep the compromise value of the strong coupling \(\alpha _s=0.3\). A discussion on the sensitivity of the result on \(\alpha _s\) and on the form of the nucleon DA used as the phenomenological input for our model can be found in Ref. [30].
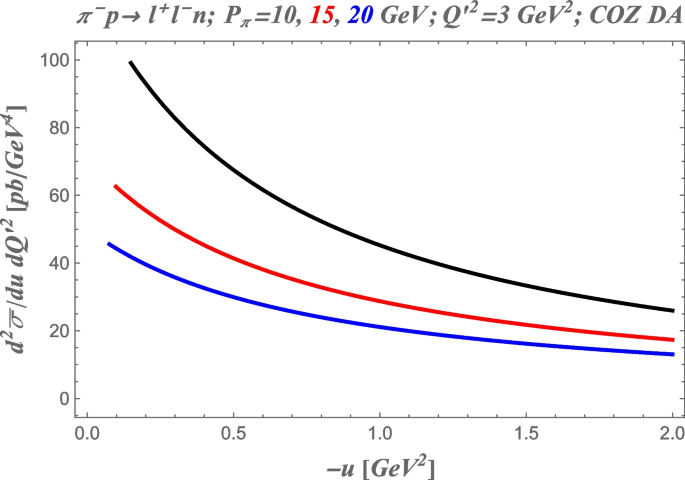
In Fig. 4, within the cross channel nucleon exchange model for \(\pi N\) TDAs (55), we present the integrated cross section (28) for backward lepton pair production
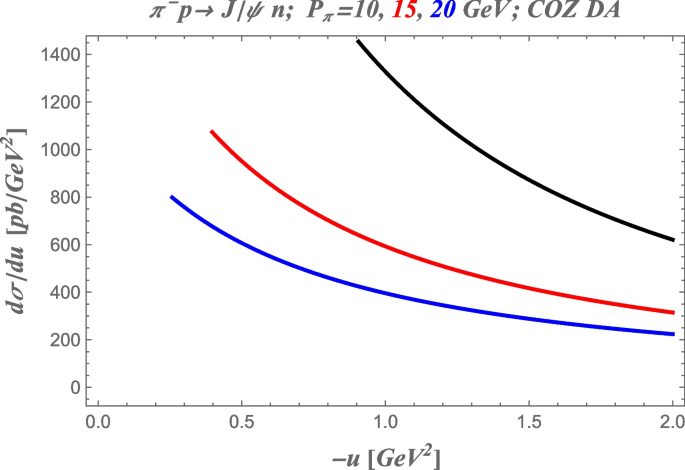
as a function of \(-u\) from the threshold value \(-u_0\) (corresponding to the exactly backward production) up to \(-u=2\) GeV\(^2\) for the three values of pion beam momentum \(P_\pi\) from the range of the J-PARC experiment [4] : \(P_\pi = 10\) GeV; \(P_\pi = 15\) GeV; \(P_\pi = 20\) GeV. The invariant mass of the lepton pair is set to \(Q'^2=3\) GeV\(^2\); the COZ [21] solution for the leading twist nucleon DA is used as the phenomenological input.
The integrated cross section for backward lepton pair production \(\frac{d^2 \bar{\sigma }}{d \Delta ^2 dQ'^2}\) as a function of \(-u\) from the threshold value \(-u_0\) (corresponding to the exactly backward production) up to \(-u=2\) GeV\(^2\) for the three values of pion beam momentum \(P_\pi\) from the range of the J-PARC experiment: \(P_\pi = 10\) GeV; \(P_\pi = 15\) GeV; \(P_\pi = 20\) GeV (from top to bottom); the invariant mass of the lepton pair \(Q'^2=3\) GeV\(^2\); the COZ [21] solution for the leading twist nucleon DA is used as the phenomenological input
In Fig. 5, we show the cross section for backward \(J/\psi\) production \(\frac{d \bar{\sigma }}{d \Delta ^2}\) (37) as a function of \(-u\) from the threshold value \(-u_0\) (corresponding to the exactly backward production) up to \(-u=2\) GeV\(^2\) within the cross channel nucleon exchange model for \(N \pi\) TDAs (55) for the same three values of pion beam momentum \(P_\pi\) : \(P_\pi = 10\) GeV; \(P_\pi = 15\) GeV; \(P_\pi = 20\) GeV; again using the COZ solution for the leading twist nucleon DA as the phenomenological input.
The cross section for backward \(J/\psi\) production \(\frac{d \bar{\sigma }}{d \Delta ^2}\) as a function of \(-u\) from the threshold value \(-u_0\) (corresponding to the exactly backward production) up to \(-u=2\) GeV\(^2\) for the three values of pion beam momentum \(P_\pi\) from the range of the J-PARC experiment \(P_\pi = 10\) GeV; \(P_\pi = 15\) GeV (from top to bottom); \(P_\pi = 20\) GeV; COZ [21] solution for the leading twist nucleon DA is used as the phenomenological input
The presented cross sections estimates give hope of experimental accessibility of the reactions at J-PARC. Dedicated feasibility studies, similar to that performed for accessing of \(\pi N\) TDAs at P̄ANDA [31, 32], extending the analysis of [4] to the near-backward kinematical regime are highly demanded to carry out a final conclusion on feasibility and prepare a detailed experimental proposal for J-PARC.
7 Data driven model estimates for near-backward \(J/\psi\) photoproduction and for TCS cross-sections
In this section, we employ the data on \(J/\psi\) photoproduction over the full near-threshold kinematic region recently presented by the GlueX collaboration in JLab [7, 19] to constrain the normalization and u-dependence of \(N\gamma\) TDAs. With help of the resulting \(N\gamma\) TDA models, we present the cross section estimates for the near-backward lepton pair photoproduction, both in the \(J/\psi\) resonance region and in the continuum (TCS), for the kinematic conditions corresponding to the recent analysis of the GlueX collaboration. The relevant values of the LAB frame photon energy \(E_\gamma\), the center-of-mass invariant energy \(W=\sqrt{m_N^2+2m_N E_\gamma }\) and the threshold values of the invariants t and u corresponding to exactly backward scattering are summarized in Table 1.
Table 1 Kinematical range of the GlueX\(J/\psi\)photoproduction experiment [19]
| \(E_\gamma\)[GeV] | W [GeV] | \(-t_1\)[GeV\(^2]\) | \(-u_0\)[GeV\(^2]\) |
|---|---|---|---|
| 8.2−9.28 | 4.04−4.28 | 3.99−6.58 | 1.54−0.98 |
| 9.28−10.36 | 4.28−4.51 | 6.58−8.84 | 0.98−0.75 |
| 10.36−11.44 | 4.51−4.73 | 8.84−11.01 | 0.75−0.61 |
A sensible estimate of the scattering amplitudes for near-backward photoproduction reactions is more difficult to justify than for the pion-beam-induced reactions. Indeed, the normalization of photon-to-nucleon TDAs is not constrained, contrarily to pion-to-nucleon TDAs which are naturally normalized in the limit \(\xi \rightarrow 1\) thanks to the soft pion chiral limit [33].
An estimate based on the hypothesis of the applicability of vector meson dominance (VMD) [34, 35] to such reactions was suggested in Ref. [11]. The nucleon-to-photon TDAs were related to the corresponding TDAs for the nucleon-to-transversely-polarized-vector-mesons, as:
where e is the electron charge and vector-meson-to-photon couplings \(f_{\rho ,\omega ,\phi }\) are estimated from \(\Gamma _{V \rightarrow e^+e^-}\) decay widths. Such a model is very constrained since data on vector meson backward electroproduction [36] exist at comparable energy and skewness. It turns out that this naive model leads to an unmeasurably small cross-section for near-backward \(J/\psi\) photoproduction. The very fact that the GlueX collaboration detects some backward scattered \(J/\psi\) mesons leads us―perhaps not surprisingly [8]―to disregard the VMD-based approach.
Let us thus try to define the various steps of a phenomenological program which may lead to a sensible extraction of at least some features of the photon to nucleon TDAs before some of their properties are discovered in non-perturbative studies such as those using lattice QCD or QCD sum-rules [37] techniques.
Since the scattering amplitudes come from the convolution of TDAs with coefficient functions integrated over the momentum fraction variables \(x_i\), the dependence of TDAs on \(x_i\) is deeply buried in observables and thus may be the least accessible feature from phenomenological studies. Such a difficulty already exists in the GPD case where it is recognized that the (\(x=\pm \xi\)) restricted domain dominance of the lowest order DVCS and TCS amplitudes calls for the study of complementary processes [38, 39].
On the contrary, the overall normalization and the u-dependence of the TDAs should be easier to access. A possible strategy is thus emerging. Firstly, we extract from our study of the transversely polarized vector meson backward electroproduction case in a simplified nucleon exchange model (60) that the integral convolutions \(\mathcal {I}^{(k)}_{\, \gamma N \rightarrow N'\left\{ \begin{array}{c} \gamma ^*\\ J/\psi \end{array}\right\} }\), \(k=1,\,3,\,4,\,5\), written in Eqs. (41), (51), turn out to be linear combinations of \(\mathcal {I}^{(k)}\)s, \(k=1,\,3,\,4,\,5\), which are proportional to the constant \(\mathcal {I}_0\) (resp. \(M_0\)) coming from the (\(x_1,x_2,x_3\)) integration in the calculation of the nucleon form factor (resp. the \(J/\psi \rightarrow \bar{p} p\) decay amplitude (57)):
Here we assume the dominance of the vector coupling of transversely polarized vector meson to nucleons \(\mathcal {L}_{VNN}^{\text {eff.}}=\bar{N} G^V_{VNN} \gamma ^\mu V_\mu N\); and the explicit expressions for the functions \(K_{1 \mathcal {E}}\), \(K_{2 \mathcal {E}}\), \(K_{1 T}\), \(K_{2 T}\), read as suggested from [25]:
The kinematical factors occurring from Eqs. (62) bring additional dependence on \(Q'^2\) and \(W^2\) through the skewness variable \(\xi\) (10). The dependence on the invariant u-channel momentum transfer \(\Delta ^2 \equiv u\) is implemented through \(G(\Delta ^2)\).
Having taken into account of the various kinematical factors, which are the same in the present processes and in our previous study of backward vector meson electroproduction [25], we are now in a position to show how one can fix the normalization and \(\Delta ^2\)-dependence of the photon to nucleon TDAs from the \(J/\psi\) photoproduction data and work out a set of predictions for the future photoproduction experiments. To achieve this goal, we propose two educated guesses for the \(\Delta ^2\)-dependence, the first one reminiscent of the cross channel nucleon exchange model:
and the second one
with positive intercept \(\alpha\) letting the amplitude fall off with \(-u\) faster than the original dipole-type formula (63). In both cases, we let the overall normalization \(C^{(1,\,2)}\) as an adjustable parameter to be fixed from the data.
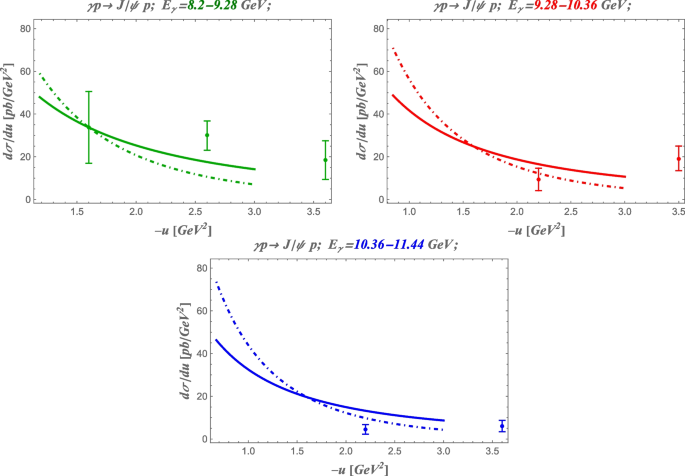
In Fig. 6, the solid lines show the predictions of the model (61) with the dipole-type u-dependence (63) for the three central values of \(E_\gamma\) from the range of the GlueX experiment [19] \(\langle E_\gamma \rangle = 8.74\) GeV; \(\langle E_\gamma \rangle = 9.82\); and \(\langle E_\gamma \rangle = 10.9\) GeV. With error bars we show the points closest to the backward threshold from the experimental data presented in Fig. 13 of [19]. Note that for the \(\langle E_\gamma \rangle = 9.82\) and \(\langle E_\gamma \rangle = 10.9\) GeV bins no data point approach close enough to threshold values of \(-u=-u_0\). We use the value of \(M_0\) computed with the COZ [21] solutionFootnote 3 for the leading twist nucleon DA as the phenomenological input and fit the value of the normalization constant \(C^{(1)}=10.9\) from the experimental cross section value corresponding to the experimental point with lowest \(-u\) (i.e. largest \(-t\)) of the \(\langle E_\gamma \rangle =8.74\) GeV bin (see the first panel of Fig. 6). This allows to present our estimates of the backward peak for the \(\langle E_\gamma \rangle = 9.82\) and \(\langle E_\gamma \rangle = 10.9\) GeV bins. Note that the GlueX data points for these bins stay too far from the backward threshold. Getting more data close to the backward threshold require augmenting the GlueX luminosity for the corresponding values of \(E_\gamma\). The suggested 17 GeV electron beam upgrade (see discussion in [41]) will provide the necessary increase in statistics to challenge the manifestation of the backward peak for higher bins in \(E_\gamma\). The estimated luminosity of the GlueX with 17 GeV electron beam results in large expected counting rates (several thousands of evens) in the vicinity of the backward peak.
Solid lines: the cross section for backward \(J/\psi\) photoproduction \(\frac{d \sigma }{d u}\) as a function of \(-u\) from the threshold value \(-u_0\) (corresponding to the exactly backward production, see Table 1) up to \(-u=3\) GeV\(^2\) for the three central values of \(E_\gamma\) from the range of the GlueX experiment \(\langle E_\gamma \rangle = 8.74\) GeV; \(\langle E_\gamma \rangle = 9.82\); and \(\langle E_\gamma \rangle = 10.9\) GeV in the model (61) with the dipole-type u-dependence (63). Dot-dashed lines show the cross sections within the TDA model with a modified normalization and u-dependence (64) with \(\alpha =0.25\) GeV\(^{-2}\). COZ [21] solution for the leading twist nucleon DA is used as the phenomenological input. With error bars we show the points closest to the backward threshold from the experimental data presented in Fig. 13 of Ref. [19]. Note that for the \(\langle E_\gamma \rangle = 9.82\) and \(\langle E_\gamma \rangle = 10.9\) GeV bins, no data point approaches close enough to threshold values of \(-u=-u_0\)
With the dot-dashed lines, we show the predictions of the TDA model with the normalization and u-dependence (64) with the value of the intercept set to \(\alpha =0.25\) GeV\(^{-2}\). The normalization constant \(C^{(2)}=16.3\) is fixed analogously to the previous case. The exponential form of u-dependence results in a narrower cross section backward peak.
Note that with our choice of the normalization constants \(C^{(1,\,2)} \simeq G_V^{\omega NN}\), see e.g. [42], the magnitude of the corresponding photon-to-nucleon TDAs turn out to be roughly of the same order as those of the nucleon-to-vector meson TDAs (multiplied by the charge factor e):
the normalization of the latter TDAs was found consistent with the experiment [36].
In order to address the universality of \(N \gamma\) TDAs through the TCS cross section measurements, we also present our estimates of near-backward TCS cross section within the \(N \gamma\) TDA models (61) with the normalization and u-dependence (63), (64) chosen to fit the GlueX \(J/\psi\) photoproduction cross section for \(E_\gamma =8.74\) GeV in the near-backward region and \(\alpha =0.25\) GeV\(^{-2}\).
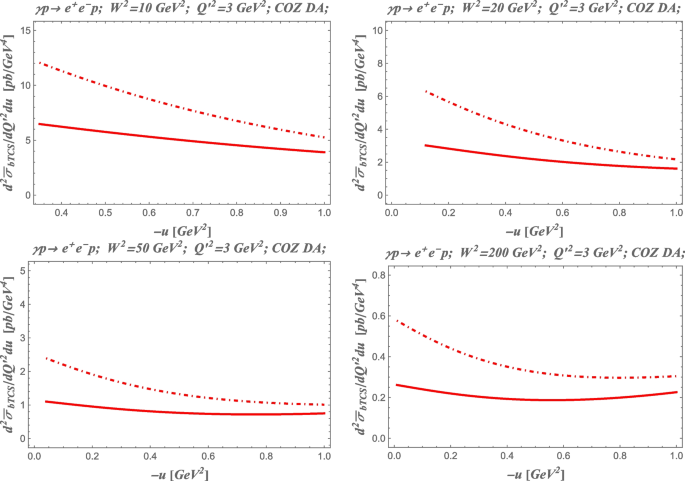
In Fig. 7, we show the cross section (46) of the near-backward \(\gamma p \rightarrow p e^+ e^-\) integrated over the lepton polar angle
as a function of \(-u\) from \(-u_0\) up to 1 GeV\(^2\). We present the cross section for several values of \(W^2\) corresponding to the kinematical range of JLab@12 GeV and JLab@24 and the future EIC and EIcC. The invariant mass squared of the lepton pair is set to \(Q'^2=3\) GeV\(^2\). We plot the cross sections as functions of \(-u\) from the minimal value \(-u_0\) up to 1 GeV\(^2\). Solid lines show the cross sections within the \(\gamma N\) TDA model with the dipole-type u-dependence (63) with overall normalization \(C^{(1)}\) adjusted to the Gluex data for \(J\psi\) photoproduction cross section in the near-backward region for \(\langle E_\gamma \rangle = 8.74\) GeV. Dot-dashed lines show the cross section estimates with the TDA model with a modified u-dependence (64) with \(\alpha = 0.25\) and the normalization \(C^{(2)}\) chosen to match the GlueX \(J/\psi\) photoproduction data. The COZ solution is employed as input phenomenological solution for nucleon DAs.
The near-backward \(\gamma p \rightarrow p e^+ e^-\) scattering cross section (66) for several values of \(W^2\); \(Q'^2=3\) GeV\(^2\); as a function of \(-u\) from the minimal value \(-u_0\) up to 1 GeV\(^2\) in the \(\gamma N\) TDA model (61). Solid lines show the cross section estimates within the TDA model with the dipole-type u-dependence (63); dot-dashed lines: the cross sections from the TDA model with modified u-dependence (64) with \(\alpha = 0.25\) GeV\(^{-2}\). Normalization is fixed from the \(J/\psi\) photoproduction data, as explained above. COZ solution is employed as input phenomenological solution for nucleon DAs
The Bethe-Heitler background cross section for TCS reaction has been estimated in Ref. [11] in the near backward region and found to be negligibly small apart from the very narrow peaks in the vicinity of \(\theta _\ell =0\). Its contribution into the integrated cross section (66) can, therefore, be safely neglected.
Let us stress that it is essential to firmly establish the physical normalization of \(N \gamma\) TDAs and to develop a reliable framework to model them in the complete domain of their definition. A possible approach can be the calculations performed within the light-cone quark model of Ref. [43] or the QCD sum-rules techniques [37]. Lattice QCD calculations might also help to get some constraints on these TDAs.
The essence of our implementation of the \(N\gamma\) TDA framework is addressing the universality of manifestation of the backward peak from the collinear factorization mechanism involving \(N\gamma\) TDAs. We fit our TDA model to match the backward peak revealed for \(J/\psi\) photoproduction by the GlueX collaboration in the lowest bin in \(E_\gamma\). This requires that the normalization of \(N \gamma\) TDAs be roughly that of nucleon-to-vector meson TDAs, the latter being to some expend tested experimentally. This implies that the backward peak must be also manifest in other \(E_\gamma\) bins for \(J/\psi\) photoproduction by the GlueX as well as in the backward TCS reaction.
The suggested 17 GeV upgrade of the GlueX experiment will provide enough statistics to confirm or reject the manifestation of the backward peak required by the universality of \(N\gamma\) TDAs. This will bring strong arguments to make a decision on the validity of the collinear factorization framework for backward photoproduction reactions and will allow a more detailed comparison with predictions from alternative reaction mechanisms [44,45,46].
Also, the magnitude of the near-backward TCS cross section from the \(\gamma N\) TDA models (61) with u-dependence (63), (64), and normalization adjusted to the GlueX \(J/\psi\) photoproduction data in the near-backward region is considerably larger than the predictions made from the pure VMD-based cross channel nucleon exchange model [11]. An observation of a sizable backward peak for TCS cross section would provide a crucial test for the verification of the universality of TDAs and hence of the consistency of the QCD approach to backward hard exclusive reactions.
8 Conclusions
This short review of the applications of the TDA concept in exclusive reactions initiated by a photon or a \(\pi\)-meson beam illustrates the ability of the QCD collinear factorization approach to describe high invariant mass dilepton and heavy quarkonium production amplitudes in terms of meson-to-nucleon and photon-to-nucleon TDAs in a new kinematical window, complementary to the forward kinematics, where GPDs play a leading role. In particular, the comparison between backward timelike virtual photon and backward charmonium production, i.e. dilepton production at or off the resonance peak at the \(J/\psi\) mass, will offer a clear cut proof of the validity of a partonic interpretation of backward exclusive scattering. It also would be instructive to compare the predictions of QCD collinear factorization approach with that of the Regge theory framework [44, 45] within the near-backward kinematics.
Let us stress that working out predictions that may allow to really distinguish between the Regge-based approach and the collinear factorization approach in the backward regime is a tricky task. Recent Regge analysis of backward meson electroproduction in Ref. [47] demonstrates that by including the contribution of box diagrams in the backward kinematics a consistent description of the JLab experimental data can be achieved based on the Regge approach. The two description can be seen as sort of dual in the kinematical domain in which factorization can be justified.
We did not cover the deep electroproduction processes [25, 33] nor the antiproton―nucleon annihilation case [48] that we studied earlier in a quite detailed way. We believe that near future studies at JLab as well as at future experimental facilities [16, 18, 49] will test the universality of TDAs extracted from various processes. Anyhow, the study of hard exclusive reactions in the backward region will provide very interesting data that should drastically improve our understanding of the baryonic structure.
Availability of data and materials
Not applicable.
Notes
-
We assume the use of the light-cone gauge \(A^+ \equiv 2 (A \cdot n)=0\) and omit the Wilson lines along the light-like path.
-
The indexes \(k=1,3,4,5\) were chosen to match the notations established for the description of near-backward vector meson electroproduction in Ref. [25].
-
DA solutions with a shape close to the asymptotic form [27] are known to largely underestimate the value of \(J/\psi \rightarrow N\bar{N}\) decay width with the leading twist-3 pQCD description since the \(M_0\) constant appears to be too small for the compromise value of \(\alpha _s \simeq 0.3\); see discussion in Ref. [40].
References
-
D. Müller, D. Robaschik, B. Geyer, F.M. Dittes, J. Hořejši, Wave functions, evolution equations and evolution kernels from light ray operators of QCD. Fortsch. Phys. 42, 101–141 (1994). https://doi.org/10.1002/prop.2190420202
-
E.R. Berger, M. Diehl, B. Pire, Time-like Compton scattering: exclusive photoproduction of lepton pairs. Eur. Phys. J. C 23, 675–689 (2002). https://doi.org/10.1007/s100520200917
-
E.R. Berger, M. Diehl, B. Pire, Probing generalized parton distributions in \(\pi N \rightarrow \ell ^+ \ell ^- N\). Phys. Lett. B 523, 265–272 (2001). https://doi.org/10.1016/S0370-2693(01)01345-4
-
T. Sawada, W.C. Chang, S. Kumano, J.C. Peng, S. Sawada, K. Tanaka, Accessing proton generalized parton distributions and pion distribution amplitudes with the exclusive pion-induced Drell-Yan process at J-PARC. Phys. Rev. D 93(11), 114034 (2016). https://doi.org/10.1103/PhysRevD.93.114034
-
D. Müller, B. Pire, L. Szymanowski, J. Wagner, On timelike and spacelike hard exclusive reactions. Phys. Rev. D 86, 031502 (2012). https://doi.org/10.1103/PhysRevD.86.031502
-
P. Chatagnon et al., First measurement of timelike Compton scattering. Phys. Rev. Lett. 127(26), 262501 (2021). https://doi.org/10.1103/PhysRevLett.127.262501
-
A. Ali et al., First measurement of near-threshold J/\({\psi }\) exclusive photoproduction off the proton. Phys. Rev. Lett. 123(7), 072001 (2019). https://doi.org/10.1103/PhysRevLett.123.072001
-
T.S.H. Lee, S. Sakinah, Y. Oh, Models of \(J/Psi\) photo-production reactions on the nucleon. Eur. Phys. J. A 58(12), 252 (2022). https://doi.org/10.1140/epja/s10050-022-00901-9
-
P. Sun, X.B. Tong, F. Yuan, Near threshold heavy quarkonium photoproduction at large momentum transfer. Phys. Rev. D 105(5), 054032 (2022). https://doi.org/10.1103/PhysRevD.105.054032
-
B. Pire, K. Semenov-Tian-Shansky, L. Szymanowski, Backward charmonium production in \(\pi N\) collisions. Phys. Rev. D 95(3), 034021 (2017). https://doi.org/10.1103/PhysRevD.95.034021
-
B. Pire, K.M. Semenov-Tian-Shansky, A.A. Shaikhutdinova, L. Szymanowski, Backward timelike Compton scattering to decipher the photon content of the nucleon. Eur. Phys. J. C 82(7), 656 (2022). https://doi.org/10.1140/epjc/s10052-022-10587-4
-
B. Pire, K. Semenov-Tian-Shansky, L. Szymanowski, Transition distribution amplitudes and hard exclusive reactions with baryon number transfer. Phys. Rept. 940, 2185 (2021). https://doi.org/10.1016/j.physrep.2021.09.002
-
C.A. Gayoso et al., Progress and opportunities in backward angle (\(u\)-channel) physics. Eur. Phys. J. A 57(12), 342 (2021). https://doi.org/10.1140/epja/s10050-021-00625-2
-
W.B. Li, et al., Backward-angle exclusive \(\pi ^0\) production above the resonance region. arXiv:2008.10768 [nucl-ex] (2020)
-
K. Aoki, et al., Extension of the J-PARC Hadron Experimental Facility: Third White Paper. arXiv:2110.04462 [nucl-ex] (2021)
-
R. Abdul Khalek et al., Science requirements and detector concepts for the electron-ion collider: EIC Yellow Report. Nucl. Phys. A 1026, 122447 (2022). https://doi.org/10.1016/j.nuclphysa.2022.122447
-
V. Burkert et al., Precision studies of QCD in the low energy domain of the EIC. Prog. Part. Nucl. Phys. 131, 104032 (2023). arXiv:2211.15746 [nucl-ex]
-
D.P. Anderle et al., Electron-ion collider in China. Front. Phys. (Beijing) 16(6), 64701 (2021). https://doi.org/10.1007/s11467-021-1062-0
-
S. Adhikari et al., Measurement of the J/\(\psi\) photoproduction cross section over the full near-threshold kinematic region. Phys. Rev. C 108, 025201 (2023). arXiv:2304.03845 [nucl-ex]
-
B. Pire, K. Semenov-Tian-Shansky, L. Szymanowski, \(\pi N\) transition distribution amplitudes: their symmetries and constraints from chiral dynamics. Phys. Rev. D 84, 074014 (2011). https://doi.org/10.1103/PhysRevD.84.074014
-
V.L. Chernyak, A.A. Ogloblin, I.R. Zhitnitsky, Calculation of exclusive processes with baryons. Z. Phys. C 42, 583 (1989). https://doi.org/10.1007/BF01557664. [Yad. Fiz.48, 1398 (1988); Sov. J. Nucl. Phys.48, 889 (1988)]
-
J.P. Lansberg, B. Pire, L. Szymanowski, Hard exclusive electroproduction of a pion in the backward region. Phys. Rev. D 75, 074004 (2007). https://doi.org/10.1103/PhysRevD.75.074004. [Erratum: Phys.Rev.D 77, 019902 (2008)]
-
V.L. Chernyak, A.R. Zhitnitsky, Asymptotic behavior of exclusive processes in QCD. Phys. Rept. 112, 173 (1984). https://doi.org/10.1016/0370-1573(84)90126-1
-
R.L. Workman, Others, Review of particle physics. PTEP 2022, 083C01 (2022). https://doi.org/10.1093/ptep/ptac097
-
B. Pire, K. Semenov-Tian-Shansky, L. Szymanowski, QCD description of backward vector meson hard electroproduction. Phys. Rev. D 91(9), 094006 (2015). https://doi.org/10.1103/PhysRevD.91.094006. [Erratum: Phys. Rev. D 106, 099901 (2022)]
-
J. Bolz, P. Kroll, Modeling the nucleon wave function from soft and hard processes. Z. Phys. A 356, 327 (1996). https://doi.org/10.1007/s002180050186
-
V.M. Braun, A. Lenz, M. Wittmann, Nucleon form factors in QCD. Phys. Rev. D 73, 094019 (2006). https://doi.org/10.1103/PhysRevD.73.094019
-
J.Y. Kim, H.C. Kim, M.V. Polyakov, Light-cone distribution amplitudes of the nucleon and \(\Delta\) baryon. JHEP 11, 039 (2021). https://doi.org/10.1007/JHEP11(2021)039
-
I.V. Musatov, A.V. Radyushkin, Transverse momentum and Sudakov effects in exclusive QCD processes: Gamma* gamma pi0 form-factor. Phys. Rev. D 56, 2713–2735 (1997). https://doi.org/10.1103/PhysRevD.56.2713
-
B. Pire, K. Semenov-Tian-Shansky, L. Szymanowski, QCD description of charmonium plus light meson production in \(\bar{p}-N\) annihilation. Phys. Lett. B 724, 99–107 (2013). https://doi.org/10.1016/j.physletb.2013.06.015. [Erratum: Phys. Lett. B 764, 335–335 (2017)]
-
B.P. Singh et al., Experimental access to transition distribution amplitudes with the \(\bar{\text{P}}\)ANDA experiment at FAIR. Eur. Phys. J. A 51(8), 107 (2015). https://doi.org/10.1140/epja/i2015-15107-y
-
B. Singh et al., Feasibility study for the measurement of \(\pi N\) transition distribution amplitudes at \(\bar{\text{ P }}\)ANDA in \(\bar{p}p\rightarrow J/\psi \pi ^0\). Phys. Rev. D 95(3), 032003 (2017). https://doi.org/10.1103/PhysRevD.95.032003
-
J.P. Lansberg, B. Pire, K. Semenov-Tian-Shansky, L. Szymanowski, A consistent model for \(\pi N\) transition distribution amplitudes and backward pion electroproduction. Phys. Rev. D 85, 054021 (2012). https://doi.org/10.1103/PhysRevD.85.054021
-
T. Hakioglu, M.D. Scadron, Vector meson dominance, one loop order quark graphs, and the chiral limit. Phys. Rev. D 43, 2439–2442 (1991). https://doi.org/10.1103/PhysRevD.43.2439
-
D. Schildknecht, Vector meson dominance. Acta Phys. Polon. B 37, 595–608 (2006). arXiv:hep-ph/0511090
-
W.B. Li et al., Unique access to \(u\)-channel physics: exclusive backward-angle omega meson electroproduction. Phys. Rev. Lett. 123(18), 182501 (2019). https://doi.org/10.1103/PhysRevLett.123.182501
-
U. Haisch, A. Hala, Semi-leptonic three-body proton decay modes from light-cone sum rules. JHEP 11, 144 (2021). https://doi.org/10.1007/JHEP11(2021)144
-
J.W. Qiu, Z. Yu, Single diffractive hard exclusive processes for the study of generalized parton distributions. Phys. Rev. D 107(1), 014007 (2023). https://doi.org/10.1103/PhysRevD.107.014007
-
K. Deja, V. Martinez-Fernandez, B. Pire, P. Sznajder, J. Wagner, Phenomenology of double deeply virtual Compton scattering in the era of new experiments. Phys. Rev. D. 107 (9), 094035 (2023). https://doi.org/10.1103/PhysRevD.107.094035
-
N.G. Stefanis, The Physics of exclusive reactions in QCD: theory and phenomenology. Eur. Phys. J. direct 1(1), 7 (1999). https://doi.org/10.1007/s1010599c0007
-
L. Pentchev, New opportunities for \(J/\psi\) (and beyond) photoproduction studies in Hall D with the CEBAF upgrade. A talk presented at “Opportunities with JLab Energy and Luminocity Upgrade”, ECT\(^*\) Trento, Italy, 26-30 September 2022. https://indico.ectstar.eu/event/152/contributions/3133/attachments/2001/2612/LPentchev_Jpsi_Trento.pdf. Accessed 2023
-
R. Machleidt, The high precision, charge dependent Bonn nucleon-nucleon potential (CD-Bonn). Phys. Rev. C 63, 024001 (2001). https://doi.org/10.1103/PhysRevC.63.024001. Accessed 2001
-
B. Pasquini, M. Pincetti, S. Boffi, Parton content of the nucleon from distribution amplitudes and transition distribution amplitudes. Phys. Rev. D 80, 014017 (2009). https://doi.org/10.1103/PhysRevD.80.014017
-
B.G. Yu, K.J. Kong, Features of \(\omega\) photoproduction off proton target at backward angles : role of nucleon Reggeon in \(u\)-channel with parton contributions. Phys. Rev. D 99(1), 014031 (2019). https://doi.org/10.1103/PhysRevD.99.014031
-
I.I. Strakovsky, W.J. Briscoe, O.C. Becerra, M. Dugger, G. Goldstein, V.L. Kashevarov, A. Schmidt, P. Solazzo, B.G. Yu, Pseudoscalar and scalar meson photoproduction interpreted by Regge phenomenology. Phys. Rev. C 107(1), 015203 (2023). https://doi.org/10.1103/PhysRevC.107.015203
-
I. Strakovsky, W.J. Briscoe, E. Chudakov, I. Larin, L. Pentchev, A. Schmidt, R.L. Workman, Is the LHCb \(P_c(4312)^+\) plausible in the GlueX \(\gamma p\rightarrow J/\psi p\) total cross sections. Phys. Rev. C 108, 015202 (2023). arXiv:2304.04924 [hep-ph]
-
J.M. Laget, Unitarity constraints on meson electroproduction at backward angles. Phys. Rev. C 104(2), 025202 (2021). https://doi.org/10.1103/PhysRevC.104.025202
-
J.P. Lansberg, B. Pire, K. Semenov-Tian-Shansky, L. Szymanowski, Accessing baryon to meson transition distribution amplitudes in meson production in association with a high invariant mass lepton pair at GSI-FAIR with \(\bar{\text{ P }}\)ANDA. Phys. Rev. D 86, 114033 (2012). https://doi.org/10.1103/PhysRevD.86.114033. [Erratum: Phys. Rev. D 87, 059902 (2013)]
-
M.F.M. Lutz, et al., Physics Performance Report for \(\bar{\text{ P }}\)ANDA: Strong Interaction Studies with Antiprotons. arXiv:0903.3905 [hep-ex] (2009)
Acknowledgements
We acknowledge useful and inspiring discussions with Shunzo Kumano, Bill Li, Zein-Eddine Meziani, Yongseok Oh, and Lubomir Pentchev. We also thank both anonymous referees for their careful reports that helped us to improve our paper.
Funding
This work was supported in part by the European Union’s Horizon 2020 research and innovation program under Grant Agreement No. 824093 and by the LABEX P2IO. The work of K.S. is supported by the Foundation for the Advancement of Theoretical Physics and Mathematics “BASIS” and by the National Research Foundation of Korea (NRF) under Grants No. NRF-2020R1A2C1007597 and No. NRF-2018R1A6A1A06024970 (Basic Science Research Program). The work of A.S. is supported by the Foundation for the Advancement of Theoretical Physics and Mathematics “BASIS”. The work of L.S. is supported by the grant 2019/33/B/ST2/02588 of the National Science Center in Poland.
Author information
Authors and Affiliations
Contributions
All authors made significant contributions into this paper.
Corresponding author
Ethics declarations
Ethical ppproval and consent to participate
Not applicable.
Consent for publication
All authors have provided their consent for publication.
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
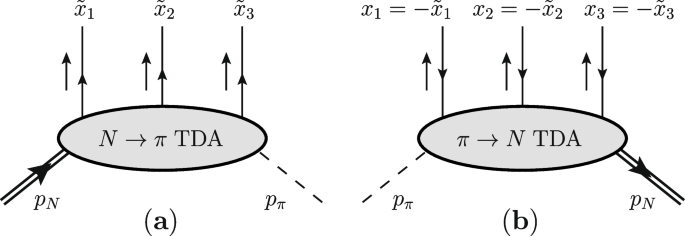
Appendix A: Crossing \(\pi \rightarrow N\) TDAs to \(N \rightarrow \pi\) TDAs
The study of electroproduction processes [22] lead us to parameterize the nucleon-to-pion (\(\pi N\)) TDAs defined through the Fourier transform of the \(\pi N\) matrix element of the trilinear quark operator on the light cone. The parametrization involves eight invariant functions each being the function of three longitudinal momentum fractions, skewness variable, momentum transfer squared as well as of the factorization scale.
Let us consider the neutron-to-\(\pi ^-\) uud TDA. We make use of the parametrization of Ref. [22], where only three invariant functions turn out to be relevant in the \(\Delta _T=0\) limit:
We adopt Dirac’s “hat” notation \(\hat{v} \equiv v_\mu \gamma ^\mu\); \(\sigma ^{\mu \nu }= \frac{1}{2} [\gamma ^\mu , \gamma ^\nu ]\); \(\sigma ^{v \mu } \equiv v_\lambda \sigma ^{\lambda \mu }\); C is the charge conjugation matrix and \(U^+= \hat{p} \hat{n} \, U(p_N,s_N)\) is the large component of the nucleon spinor; and employ compact notations for the set of the relevant Dirac structures \(s^{\pi N} \equiv \{ a^{ \pi N}_{1,2} , \, a^{ \pi N}_{1,2}, \, t^{ \pi N}_{1,2,3,4} \}\).
Note that the \(\pi N\) TDA (67) is defined with respect to the natural kinematical variables of \(\gamma ^* N \rightarrow \pi N'\) reaction. Namely the cross channel momentum transfer is \(\tilde{\Delta }=p_\pi -p_N\) and the skewness parameter \(\tilde{\xi }\) is defined from the longitudinal momentum transfer between pion and nucleon
(i.e. it differs by the sign from the definition (8) natural for the reactions (1) in the near-backward regime).
In order to express pion-to-nucleon (\(N \pi\)) TDAs through (\(\pi N\)) TDAs occurring in (67) we apply the Dirac conjugation (complex conjugation and convolution with \(\gamma _0\) matrices in the appropriate spinor indices) for both sides of eq. (67) and compare the result to the definition of \(\pi N\) TDAs:
For the relevant Dirac structures occurring in the parametrization (19) we get
where we switch to the definition of momentum transfer natural for the timelike reactions: \(\tilde{\Delta } \rightarrow -\Delta\). \(\bar{U}^+\equiv \bar{U}(p_N) \hat{n} \hat{p}\) stands for the large component of the \(\bar{U}(p_N)\) Dirac spinor.
The flow of the longitudinal momentum for \(N \rightarrow \pi\) TDAs defined as in eq. (67) and \(\pi \rightarrow N\) TDAs is presented on Fig. 8. By switching to the variables \(\xi =-\tilde{\xi }\) and \(x_i=-\tilde{x}_i\) natural for the timelike reactions and \(\tilde{\Delta }^2 \rightarrow \Delta ^2\) we conclude that
Small arrows show the direction of the longitudinal momentum flow in the ERBL-like regime for a: The longitudinal momentum flow for nucleon-to-pion (\(\pi N\)) TDAs defined in (67). The longitudinal momentum transfer is \((p_\pi -p_N) \cdot n \equiv \tilde{\Delta } \cdot n\). b: The longitudinal momentum flow for pion-to-nucleon (\(N \pi\)) TDAs defined in (19). The longitudinal momentum transfer is \((p_N-p_\pi ) \cdot n \equiv \Delta \cdot n\). Arrows on the nucleon and quark (antiquark) lines show the direction of flow of the baryonic charge
The set of the Dirac structures for photon-to-nucleon (\(N \gamma\)) TDAs can be established according to the pattern of Eq. (68) employing the set of the Dirac structures for photon-to-nucleon TDAs summarized in Appendix of Ref. [11]. The set of relations between nucleon-to-photon and photon-to-nucleon TDAs is fully analogous to Eq. (70).
Appendix B: Backward charmonium production amplitudes
1.1 Backward \(J/\psi\) pion-production amplitude
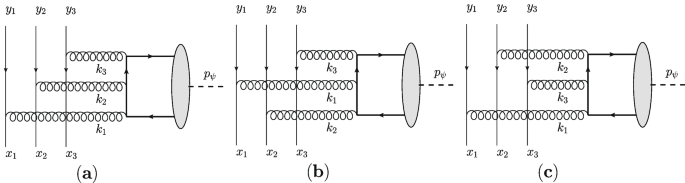
The amplitude of backward charmonium production (32) was computed in [10] from the 3 leading twist-3 diagrams presented in Fig. 9. These diagrams are analogous to those familiar from the calculation of the charmonium decay width (see e.g. Ref. [21]) dominated by the transverse polarization of the charmonium.
Here we quote the result for the integral convolutions \({\mathcal {J}}^{(1,2)}_{\pi N \rightarrow N' J/\psi }(\xi ,\Delta ^2)\) of hard kernels with \(N \pi\) TDAs, nucleon DAs and non-relativistic light-cone wave function of \(J/\psi\):
The expressions (71), (72) have structure similar to the well known convolution of nucleon DAs with hard scattering kernel occurring in the \(J/\psi \rightarrow \bar{p} p\) decay amplitude (57) [21]:
1.2 Backward \(J/\psi\) photoproduction amplitude
The amplitude of backward \(J/\psi\) photoproduction off nucleons (50) is calculated from the same 3 diagrams presented in Fig. 9. It yields the following result for the convolutions \({{\mathcal {J}}}^{(1,3,4,5)}_{\gamma N \rightarrow N' J/\psi }(\xi ,\Delta ^2)\)