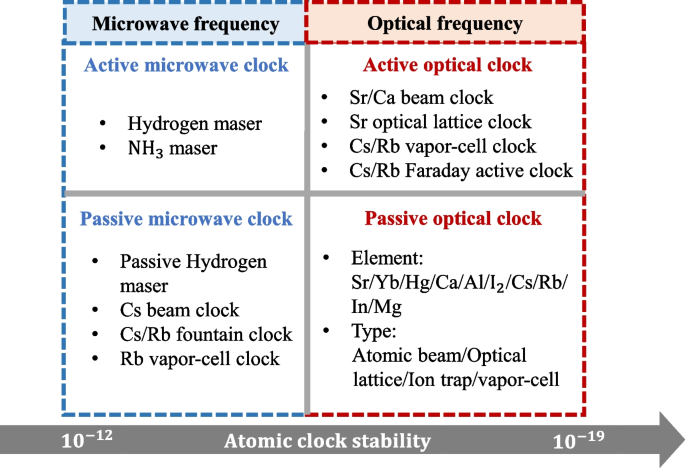
As the most precise scientific device, atomic clocks are widely used in numerous fields, such as military and national defense, cosmic exploration [1,2,3], and scientific frontier research [4,5,6]. According to operating frequency, atomic clocks can be divided into microwave clocks and optical clocks. The optical clocks, operating at frequency domain by about five orders of magnitudes higher than that of the microwave clocks, have been surpass the performance of microwave clocks both in stability and uncertainty. The stability of state-of-the-art optical clocks has reached the magnitude of \(10^{-19}\) [7, 8], which means it can verify general relativity within millimeter dimensions [9]. Atomic clocks also can be divided into two categories according to their working mode, namely passive clocks and active clocks (see Fig. 1). The passive clocks, whose standard frequency is locked to an ultra-narrow atomic spectral line, such as, laser cooled Cs beam or lattice trapped Sr atoms, depend on spontaneous emission line. On the contrary, the active clocks [10], in which the atoms are used as gain medium, are based on the stimulated emission radiation, their spectrum can be directly used as the frequency standard.

Currently, two types of optical clocks with the best performance are both passive clocks, which are optical lattice clocks [7, 11, 12] and ion optical clocks [8, 13, 14]. Since the observation of the strongly forbidden \(^{1}\textrm{S}_{0}\) \(\rightarrow\) \(^{3}\textrm{P}_{0}\) transition can be used as a clock transition by Lemonde et al. [15] and Katori et al. [16] in 2003, Sr optical lattice clocks have developed rapidly. After that, the National Institute of Standards and Technical (NIST), the Physikalisch-Technische Bundesanstalt (PTB), the Observatoire de Paris, the National Research Council (NRC), the Joint Institute of Laboratory Astrophysics (JILA), the University of Tokyo, National Institute of Information and Telecommunications Technology (NICT), and others have conducted intensive research on Sr optical lattice clocks. Currently, the frequency stability of the Sr optical lattice clock can reach \(4.8\times 10^{-17}/\sqrt{\tau }\) [11], and the system uncertainty can reach \(2\times 10^{-18}\) [17]. In addition, the Yb optical lattice clock achieves a frequency stability of \(1.5\times 10^{-16}/\sqrt{\tau }\), a long-term frequency stability of \(3.2\times 10^{-19}\) [7], and a system uncertainty of \(1.4\times 10^{-18}\) [18]. By cross-referencing with the Sr optical lattice clock, the relative frequency uncertainties of the Hg optical lattice clocks achieved \(1.8\times 10^{-16}\) [12] and \(8.4\times 10^{-17}\) [19], respectively. The National Institute of Metrology (NIM) of China has realized the evaluation and absolute frequency measurement of Sr optical lattice clock with a system uncertainty up to \(2.8\times 10^{-17}\) [20, 21] and a frequency stability of \(1.8\times 10^{-15}/\sqrt{\tau }\) [22]. The system uncertainty of Yb optical lattice clock developed by East China Normal University reaches \(1.7\times 10^{-16}\) [23].

In recent years, breakthroughs have also been made in ion-trapped optical clocks. In the 1980s, Dehmelt’s group proposed the idea of using the Paul trap to imprison ions. Subsequently, the ion-trapped optical clocks with \(\textrm{Hg}^{+}\) [24], \(\textrm{Sr}^{+}\) [25], \(\textrm{Yb}^{+}\) [13], \(\textrm{Al}^{+}\) [8, 26], and \(\textrm{Ca}^{+}\) [27, 28] ions as quantum references developed rapidly. Among them, the PTB achieves a \(\textrm{Yb}^{+}\) optical clock with a system uncertainty of \(3\times 10^{-18}\) [13] and tests the principle of local position invariance [29]. The NIST’s \(\textrm{Al}^{+}\) optical clock has reached the \(10^{-19}\) order of magnitude for system frequency accuracy assessment [8]. In addition, the system frequency uncertainty of the \(\textrm{Ca}^{+}\) optical clock realized by the Wuhan Institute of Physics and Mathematics (WIPM) of Chinese Academy of Sciences is \(5.1\times 10^{-17}\), and the frequency stability reaches \(7\times 10^{-17}\) at an average time of 20,000 s [28]. Recently, Cao et al. reported a robust, compact, and transportable \(^{40}\textrm{Ca}^{+}\) single-ion optical clock with a system uncertainty of \(1.1\times 10^{-17}\), and the frequency stability reaches \(1.5\times 10^{-17}\) near 100,000 s [30].

In order to detect atomic transition spectra with mHz linewidth, the local oscillator linewidth must be narrow enough. At present, the ultra-narrow linewidth laser sources with low phase noise and high coherence are mainly obtained by Pound-Drever-Hall (PDH) technique [31, 32]. It requires resonant cavity mirrors with high reflectivity coatings to achieve \(10^{6}\) or higher finesse. To reduce the thermal noise of the resonant cavity [33], it is necessary to use single crystal silicon or microcrystalline glass with ultra-low thermal expansion coefficient as the cavity material [34]. In addition, the resonant cavity needs to be placed in an ultra-low temperature environment to reduce frequency drift [35,36,37]. However, even with the most stable resonant cavitiy, the stabilized laser is subject to cavity-length thermal noise, which causes phase drift that limits the laser linewidth to \(0.125-0.3\,\textrm{Hz}\) [38, 39]. Using super-stable resonant cavity results in expensive cost and complex systems, is environmentally sensitive, and does not solve the cavity-length thermal noise problem essentially.

To overcome the problem that the optical cavity used for frequency stabilization is limited by thermal noise, Chen proposed the concept of active optical clock (AOC) in 2005 [10, 40]. After the AOC was proposed, it received wide attention from international peers. In the 2015 IEEE International Frequency Control Symposium (IFCS), the AOC was listed as one of the three most emerging technologies receiving the most attention in this field. Currently, there are research groups across the globe such as JILA [41,42,43], NIST, University of Colorado, Vienna University of Technology (TU Wien) [44, 45], University of Copenhagen [46], University of Amsterdam [47, 48], Aarhus University [49, 50], Zhengzhou University [51, 52], Physical Research Laboratory (India) [53], University of Hamburg [54], University of Innsbruck [55, 56], Leibniz University Hannover [57], Nicolaus Copernicus University [58], Academia Sinica [59], Guru Nanak Dev University [60], Université Sorbonne Paris Nord [61], and Peking University [53, 62] conducting research on bad-cavity superradiant laser based on various atomic systems. Currently, the JILA research group achieves a superradiant pulsed lasing based on the ultra-narrow transition linewidth of \(^{87}\textrm{Sr}\) atoms with a frequency stability of \(6.7\times 10^{-16}\) at 1 s and an accuracy of \(4\times 10^{-15}\) [43]. The University of Hamburg realizes a hyperbolic sinusoidal superradiant light field based on \(^{40}\textrm{Ca}\) atom with intensity proportional to the particle number squared [54]. The Niels Bohr Research at the University of Copenhagen demonstrates a pulsed superradiant signal based on \(^{88}\textrm{Sr}\) [46]. The Aarhus University realizes superradiant pulsed laser with linewidth less than 2 Hz [49]. The Peking University achieves a continuous-wave (CW) 1470 nm active light field based on Cs thermal atoms with a linewidth of 53 Hz and demonstrate its superior cavity-pulling suppression property [62].

Compared to passive optical clocks, AOCs output an optical frequency standard directly based on the principle of stimulated radiation. Since it works in the bad-cavity region, which means the cavity-mode linewidth is larger than the atomic gain linewidth, it can effectively solve the cavity-length thermal noise problem of passive optical clocks based on PDH technique. AOC has important application prospects and research significance in a lot of fields, such as precision scientific measurement, physical theory verification, quantum simulation, and gravitational detection.

In this paper, we start with the origin of AOC. In Section 2, we will focus on the fundamental principles of AOC. We then review the scheme of AOC in Section 3, which are classified into two-, three- and four-level according to the quantum reference transition energy levels. In Section 4, we present some applications of AOC. Section 5 provides a summary and outlook.

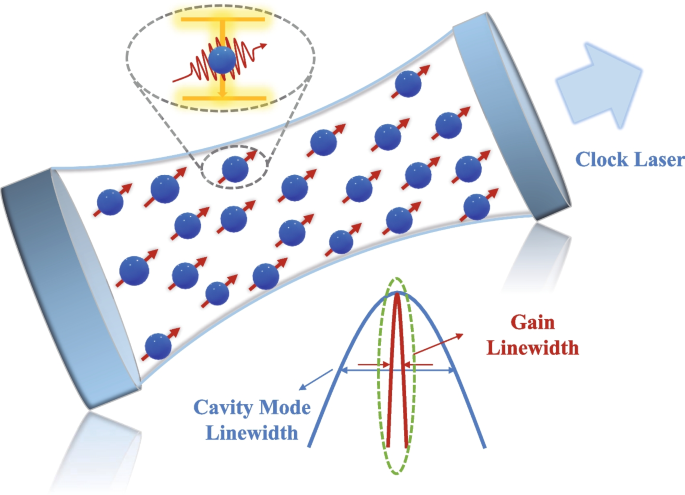
In AOC, multi-atom coherent stimulated radiation is formed between atomic transition levels through the weak feedback of optical resonator; the schematic diagram of the AOC is shown in Fig. 2. AOCs are based on the principle of stimulated radiation, in which atoms are pumped to the excited state under the action of pumping light, creating a population inversion between two energy levels. These atoms that have achieved population inversion are placed in an optical resonant cavity as the gain medium of the clock transition. Under the weak feedback of the cavity, the coherent radiation output is realized as an active optical frequency standard. Due to the phase coherence of collective dipole emission, the output laser has excellent phase coherence, which can exceed the quantum-limited linewidth determined by spontaneous emission [42, 63]. AOC is an innovative way to obtain high coherence, ultra-narrow linewidth lasers. Using quantum reference system as gain medium, its stimulated radiation can be directly used as the clock laser. Conventional passive optical clocks work in good-cavity region, its local oscillator laser generally use medium with broad gain linewidth, and the cavity-mode linewidth is narrower than the gain linewidth, so its output frequency is mainly determined by the central frequency of the cavity mode. When the external environment noise causes the change of cavity length, the output laser’s frequency will change accordingly. Unlike conventional good-cavity laser, the atomic gain linewidth of AOC is narrower than the cavity-mode linewidth. Therefore, the AOC works in the bad-cavity regime. The center frequency of the clock laser depends on quantum transition frequency, which can effectively suppress the cavity-pulling effect and reduce the impact of the cavity-length thermal noise. Utilizing AOC, the laser linewidth is expected to reach mHz level [41] and the frequency stability is expected to exceed existing optical clocks. There are several advantages of AOC, as described next.

2.1 Cavity-pulling characteristic

The relationship between the center frequency \(\nu\) of AOC output laser and the frequency \(\nu _{0}\) of atomic transition frequency can be expressed as [42]

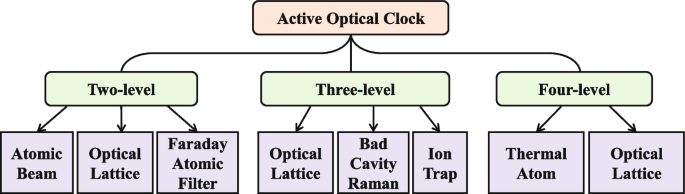
According to the energy-level structure of atoms for stimulated radiation, AOC can be divided into three categories: two-, three-, and four-level AOC. Among them, the two-level scheme includes atomic beam, Faraday atomic filter, and optical lattice type; the three-level scheme includes optical lattice, bad-cavity Raman, and ion trap type; and the four-level scheme includes thermal atom and optical-lattice-trapped cold atom type, which are shown in Fig. 3.

3.1 Two-level AOC

For two-level AOCs, international research is being carried out including JILA, Peking University, University of Copenhagen, University of Hamburg, and so on. The atoms used in the two-level AOCs are currently focused on Ca and Sr. Some properties of the two-level AOCs, including the clock transition levels, their wavelengths and working types, are given in Table 1.

3.1.1 Atomic beam two-level AOC

In terms of two-level AOCs, atomic beam type is applicable to any two-level atomic system with metastable upper state. There are abundant quantum systems available, atomic beams such as Mg [65], Ca [66], Sr [67], Ba, and molecular beams such as \(\mathrm {CH_{4}}\) [68] and \(\mathrm {OsO_{4}}\) [69]. The basic working principle of atomic beam type AOC is as follows: gaseous atoms generated by a heating oven are collimated to form an atomic beam. The atoms in the ground state are pumped to the metastable state to achieve population inversion between clock transition energy levels. After that, metastable state atoms interact with an optical resonant cavity to realize the stimulated radiation output when they reach threshold condition of laser oscillation. For different atoms, the following energy levels are available: \(\mathrm {(4s^{2})^{1}S_{0}} - \mathrm {(4s4p)^{3}P_{1}}\) for Ca atoms, \(\mathrm {(3s^{2})^{3}P_{0}} - \mathrm {(3s3p)^{3}P_{1}}\) for Mg atoms, and \(\mathrm {(5s^{2})^{1}S_{0}} - \mathrm {(5s5p)^{3}P_{1}}\) for Sr atoms.

Take the Ca atom [66] as an example to illustrate more specifically. A \(657 \, \textrm{nm}\) laser pumps the collimated Ca atoms from the ground state \(\mathrm {(4s^{2})^{1}S_{0}}\) to metastable state \(\mathrm {(4s4p)^{3}P_{1}}\), achieving a population inversion. Detection is performed with a \(423 \, \textrm{nm}\) blue laser, which is located after the pump laser and divided into two parts. One is used to transfer unpumped ground state atoms to \(\mathrm {(4s4p)^{1}P_{1}}\) for electron-shelving detection. Once the atoms are excited to metastable state, they fall back to the ground state after a few tens of centimeters of flight distance. Then, they are detected by another \(423 \, \textrm{nm}\) laser beam. In this scheme, interaction time broadening is the most dominant of all broadening mechanisms, because it is much larger than the spontaneous radiation rate at \(\mathrm {^{3}P_{1}}\). Therefore, the interaction time broadening can be considered as the atom gain linewidth, which is \(2\pi \times 150\,\textrm{kHz}\). The cavity-mode linewidth is taken as \(2\pi \times 10^{4}\,\textrm{kHz}\). With proper design of bad-cavity structure, the limiting linewidth can reach \(0.1\,\textrm{Hz}\) according to the modified Schawlow-Townes formula. However, there are two problems with the atomic beam scheme. Firstly, the remaining first-order Doppler effect due to the transverse velocity distribution leads to the broadening of gain linewidth, which can be overcome through laser cooling technology. Secondly, the second-order Doppler effect causes asymmetry in the gain profile, which becomes the main limiting factor for clock accuracy. Thus, the performance of the two-level atomic beam AOC is ultimately limited by the second-order Doppler shift, although it adapts to a wide range of two-level atomic system with metastable upper state.

Through laser cooling technique, the Doppler effect can be largely suppressed. The Niels Bohr Institute at the University of Copenhagen has chosen \(^{88}\textrm{Sr}\) atoms as a quantum reference for laser frequency stabilization based on cavity-enhanced atomic interaction, using both passive and active methods [73]. In the passive scheme [74, 75], a cavity-enhanced modulation transfer spectrum is employed and the corresponding atomic phase shift is used as an error signal. Since the atom-cavity coupling occurs in the bad-cavity regime, the cavity-pulling effect can be significantly suppressed compared to the conventional scheme of locking the local oscillator to an ultra-stable cavity. In the active scheme [46], \(2 \times 10^{7}\) \(^{88}\textrm{Sr}\) atoms are confined in a large waist cavity by laser cooling and magneto-optical trapping (MOT). The \(689\,\textrm{nm}\) \(\mathrm {^{1}S_{0}}\rightarrow \mathrm {^{3}P_{1}}\) dipole-forbidden transition with a natural linewidth of \(7.5\,\textrm{kHz}\) is used as clock transition, because it has a lifetime many orders of magnitude longer than those of dipole-allowed transitions. By applying \(689\,\textrm{nm}\) \(\pi\) pulse, the \(^{88}\textrm{Sr}\) atoms cooled to mK are excited to upper level \(\mathrm {^{3}P_{1}}\). When the cavity-mode frequency is resonant with the atomic transition, the atoms immediately establish coherence through the cavity field, achieving pulsed superradiance with high spectral purity. The laser operates in the bad-cavity region, where the photon radiation is substantially enhanced due to the collective cooperativity. Its maximum output power is close to \(1\,\mathrm {\mu W}\). On the theoretical side, the atomic beam continuous superradiant laser was studied by Université Sorbonne Paris Nord [61]. They proposed a minimalistic model to explain laser threshold, power, correlation properties, and linewidth. This model describes the dynamics of atoms entering and leaving the cavity by a Hamiltonian process, without stochastic approach. They demonstrated that the ultimate linewidth is set by the fundamental quantum fluctuations of the collective atomic dipole and the continuous superradiant regime is tied to the growth of atom-atom correlations.

Cold-atom-based superradiant lasers have proven their superior performance, but parasitic heating from atomic repumping has so far limited these systems to pulsed operation [76]. This problem can be avoided using a thermal atomic beam, because the pumping process is performed outside the cavity. JILA proposed a new type of superradiant laser using a hot atomic beam passing through an optical cavity and show that the theoretical minimum linewidth and maximum power are competitive with the best ultracoherent clock laser [70]. In this article, \(^{40}\textrm{Ca}\) and \(^{88}\textrm{Sr}\) are analyzed as examples, but of course it can be extended to other kinds of alkaline earth metal atoms. The atoms can be continuously pumped to the excited state to obtain a constant population inversion, thus overcoming the influence of Dick noise on short stability and achieving CW superradiant laser output with a theoretical linewidth of mHz level.

3.1.2 Optical lattice two-level AOC

On the basis of laser cooling, atoms can be further loaded into a magic wavelength optical lattice, which confines the atoms tightly within the Lamb-Dicke range along the cavity axis and eliminates the first-order Doppler shift more effectively. In 2016, JILA achieved the first pulsed superradiant laser at \(698\,\textrm{nm}\) (\(\mathrm {^{3}P_{0}}\rightarrow \mathrm {^{1}S_{0}}\)) using \(^{87}\textrm{Sr}\) atoms trapped in the optical lattice [71]. Experimentally, \(^{87}\textrm{Sr}\) atoms loaded into the optical lattice are prepared by a two-stage cooling process. Initial trapping and cooling are performed using the dipole-allowed \(461\,\textrm{nm}\) \(\mathrm {^{1}S_{0}}\rightarrow \mathrm {^{1}P_{1}}\) transition, and further cooling is performed using narrow linewidth \(689\,\textrm{nm}\) \(\mathrm {^{1}S_{0}}\rightarrow \mathrm {^{3}P_{1}}\) transition. Among them, the \(689\,\textrm{nm}\) laser is also used to pump \(^{87}\textrm{Sr}\) atoms from ground state \(\mathrm {^{1}S_{0}}\) to \(\mathrm {^{3}P_{1}}\). Then the atoms transfer to the upper level \(\mathrm {^{3}P_{0}}\) of clock transition via an adiabatic passage by a \(698\,\textrm{nm}\) laser. Using an \(813.4274\,\textrm{nm}\) laser, which is close to the magic wavelength, as the lattice light, imparts near equal shifts to the ground and excited states of the lasing transition so as to eliminate first-order Doppler shift. Compared with independently radiating atoms, the atomic collective emissivity is enhanced more than 10,000 times after coupling to the cavity. On this basis, JILA characterized the \(^{87}\textrm{Sr}\) atomic ultra-narrow linewidth superradiant laser in 2018 with a linewidth on the order of \(10\,\textrm{Hz}\), a frequency stability of \(6.7 \times 10^{-16}\) at 1 s, and an accuracy of \(4 \times 10^{-15}\) [43]. In this bad-cavity regime, any fluctuation (thermal or mechanical) of the cavity length has much less influence on the output laser spectrum, resulting in a cavity-pulling coefficient of \(2 \times 10^{-6}\) obtained experimentally. For the Ca atom two-level optical lattice AOC, the research group at the University of Hamburg observed a hyperbolic secant shaped superradiant pulse with intensity proportional to the square of the particle number in bad-cavity regime based on \(\mathrm {^{1}S_{0}}\rightarrow \mathrm {^{3}P_{1}}\) \(657\,\textrm{nm}\) transition [54]. The pulse duration is much shorter than the natural lifetime of the \(\mathrm {^{3}P_{1}}\) state, and its decay time fluctuations are consistent with theoretical predictions. In this work, the population inversion is achieved using incoherent pumping, which holds great promise for achieving continuous superradiant output.

Theoretically, Zhang et al. applied the Monte-Carlo wave-function method (MCWF) method [50] to calculate the superradiant pulses with different initial atomic numbers in the presence of atom loss, which is in agreement with the experimental results in Ref. [71]. Since atoms are lost rapidly in the experiment, steady-state superradiance cannot be formed. By introducing an incident flux of new atoms, the laser linewidth can theoretically reach the order of mHz despite rapid atom number fluctuations. Zhang et al. also used a stochastic mean-field theory [52] to describe active frequency measurements of pulsed superradiant emission generated by thousands of \(^{87}\textrm{Sr}\) atoms trapped in an optical cavity. This theory combines cavity quantum electrodynamics and quantum measurement theory, and treats the whole atom ensemble as ten separate subensembles with different transition frequencies. The theoretically obtained superradiant beats signal, noisy power spectra, and frequency uncertainty are in agreement with the experimental results reported in Ref. [43]. Meanwhile, this theory predicts that the short-term frequency uncertainty can reach \(7\times 10^{-17}/\sqrt{(\tau /s)}\) by using longer superradiance pulses of similar strength and by reducing the time for single measurements.

For the two-level optical lattice active superradiant laser, Gogyan et al. [58] introduced a semiclassical theory of superradiant pulses generated by alkaline earth atoms and performed a feasibility analysis for an experimental implementation using the example of \(^{40}\textrm{Ca}\) atoms, reported in Ref. [54]. The results show that the inhomogeneous optical pumping procedure has a significant effect on the superradiant pulse characteristics. University of Innsbruck has evaluated the effects of dipole-dipole interaction and collective spontaneous decay on the radiation properties of the superradiant laser [55], such as linewidth, stability, and cavity-pulling, through direct numerical simulations of minority-atom systems with different geometries and densities. Besides, they demonstrated that in the bad-cavity regime, by choosing appropriate cavity detuning parameters, atoms can be trapped and cooled by the cavity field generated by their own stimulated radiation [56]. Academia Sinica [59] theoretically investigated the effect of long-range dipole-dipole interaction on the steady-state active superradiant laser. The cavity photon number and the coherence between atoms have oscillation phenomenon with interparticle distance of the atoms. The maximal cavity photon number and the minimal spectral linewidth are located under the condition of equidistant atomic arrays, which can facilitate precision measurements and the development of next-generation optical clocks.

For the schemes mentioned above using laser-cooled atomic beams and neutral atoms trapped in optical lattices, the superradiant laser output can only be operated at pulsed mode. There is no phase coherence between different individual pulses, and the pulse duration limits the stability of the output laser. To achieve a continuous superradiant laser, sequential coupling and decoupling can be used to maintain the coherence between pulses [44]. High-speed transport of ultra-cold atoms using a red-detuned one-dimensional optical lattice has been experimentally achieved in 2006, with travel distance up to \(20\,\textrm{cm}\), transport speeds up to \(6\,\mathrm {m/s}\), and accelerations up to \(2.6 \times 10^{3}\,\mathrm {m/s^{2}}\) [77]. In the sequential coupling and decoupling scheme, a blue-detuned optical lattice traps the atoms in the Lamb-Dicke region. When an atomic ensemble is located inside the cavity and starts to radiate, a second ensemble is excited to the upper state and moves toward the cavity. Once the first ensemble completes radiation, the second ensemble enters the cavity and goes on to radiating while still maintaining the phase of the cavity. At the same time, the first ensemble exits the cavity and a new inverted ensemble is prepared. Repeating the above process, because the phase of the cavity remains constant, the superradiant pulses are also highly phase-coherent with each other. It is worth mentioning that the atoms can be prepared in the upper lasing state outside the cavity, which can circumvent perturbations due to AC Stark shift. This sequential coupling method is a promising approach towards creating an active optical frequency standard. Based on the sequential coupling method proposed by Kazakov et al. [44], JILA has recently realized the transport of atoms using a moving optical lattice. [78], which is expected to be used to realize a continuous superradiant laser.

3.1.3 Faraday type two-level AOC

Compared with the atomic beam and optical lattice scheme, the two-level Faraday type is simple in structure and easy to implement. The Faraday laser uses an anti-reflective coated laser diode as the gain medium and a Faraday atomic filter as the frequency-selective device [79]. The laser frequency can be stabilized within the transmission bandwidth of the atomic filter so that the laser linewidth can be narrowed effectively through optical feedback [80]. The AOC scheme is adopted to optimize the Faraday laser’s frequency stability and named Faraday AOC [72]. Its core principle is that the gain and quantum reference are independent of each other, thus reducing the influence of noise in the gain part on the frequency stability. The gain can be provided by materials such as semiconductors, solids, or dyes, while narrow-band atomic filters provide a frequency reference. By choosing suitable parameters to make the external cavity-mode linewidth much larger than the atomic filter bandwidth, the laser works in the bad-cavity region, thus reducing the cavity-pulling effect and improving frequency stability. Meanwhile, the laser frequency is determined by quantum transition frequency, which can be directly used as a stable frequency standard. This scheme can satisfy the laser oscillation threshold by increasing the pumping efficiency of the gain medium and obtain an active optical frequency standard with narrow linewidth by compressing the atomic filter transmission bandwidth.

Although this scheme is simple in structure, it is not easy to narrow the transmission bandwidth to natural linewidth level, leading to a significant challenge in further enhancement of bad-cavity factor. At present, the linewidth of the Faraday active optical frequency standard based on the thermal Cs atomic gas cell is at \(100 \,\textrm{Hz}\) order. It has not yet reached the theoretical value [72]. To solve this problem, cold atoms or ions can be used as quantum frequency reference mode-selecting devices [81], which can effectively suppress the Doppler effect, reduce the transmission bandwidth, enhance the cavity-pulling suppression, and thus compress the laser linewidth.

3.2 Three-level AOC

The three-level AOC includes optical lattice, ion trap, and bad-cavity Raman type. For optical lattice type, the atoms are trapped during the measurement period, so it can exploit the very narrow hyperfine-induced \(\textrm{ns}^{2}\,^{1}\textrm{S}_{0}\)-\(\textrm{nsnp}\,^{3}\textrm{P}_{0}\), such as \(^{87}\textrm{Sr}\) and \(^{88}\textrm{Sr}\). JILA research group study the bad-cavity Raman laser and implement an active magnetometer based on it. For ion-trapped three-level AOC, there are only relevant theoretical studies, and no real experimental realization has been made yet. Properties of selected three-level AOC are shown in Table 2, including the clock transitions, their wavelengths, and working types.

3.2.1 Optical lattice three-level AOC

The Peking University firstly proposed an optical lattice three-level AOC scheme in 2005 [40]. They use \(423 \,\textrm{nm}\) blue MOT and \(657 \,\textrm{nm}\) red MOT to cool the Ca atoms and then confine them in a magic wavelength optical lattice. The \(423 \,\textrm{nm}\) and \(1201 \,\textrm{nm}\) lasers are used to pump the Ca atoms from ground state \(\mathrm {^{1}S_{0}}\) to \(\mathrm {^{3}P_{2}}\) through \(\mathrm {^{1}P_{1}}\), and the atoms are concentrated in \(\mathrm {^{3}P_{1}}\) by repumping laser to form the population inversion between \(\mathrm {^{3}P_{1}}\) and \(\mathrm {^{1}S_{0}}\), thus realizing \(657 \,\textrm{nm}\) optical frequency standard. This work presents the first neutral-atom-based optical lattice AOC, which is expected to reach sub-Hz linewidth. In 2007, this group revealed that a \(1 \,\textrm{mHz}\) linewidth optical clock could be realized by exploiting the phase-matching effect of the three-level \(\Lambda\)-type \(^{88}\textrm{Sr}\) atomic system confined in magic wavelength optical lattice [63]. When the nonadiabatic interaction of two quasimonochromatic fields with the states \(\mathrm {^{1}S_{0}}\), \(\mathrm {^{1}P_{1}}\), and \(\mathrm {^{3}P_{0}}\) of \(^{88}\textrm{Sr}\) achieves phase coherence, a frequency difference field with 1 mHz linewidth will be generated by the nonlinear crystal placed in a FP cavity.

A method to obtain a laser with mHz linewidth was also proposed by the JILA research group in 2009 [41]: \(^{87}\textrm{Sr}\) atoms in an optical lattice collectively emit photons on the ultranarrow clock transition \(\mathrm {^{1}S_{0}} \rightarrow \mathrm {^{3}P_{0}}\), into the mode of a high Q optical cavity. Since the coupling between atoms and the optical field is completely collective, i.e., the phase of different atomic dipoles are perfectly coherent, and the output laser linewidth is expected to be narrower than the natural linewidth. This scheme assumes that the atoms are confined in an optical lattice within a fixed lattice point so that the interatomic coupling is maximized and these atoms are in the same phase within a specific cavity mode. Repumping lasers drive atoms from \(\mathrm {^{1}S_{0}}\) to \(\mathrm {^{3}P_{0}}\), and then atoms transfer to \(\mathrm {^{3}S_{1}}\). Due to spontaneous radiation, atoms in the \(\mathrm {^{3}S_{1}}\) state decay to the \(\mathrm {^{3}P_{2}}\) and \(\mathrm {^{3}P_{0}}\), forming Raman transition between these two states to implement sideband cooling to the vibrational ground state. Besides, the repumping lasers also pump all atoms to the \(\mathrm {^{3}P_{0}}\) metastable level, thus satisfying inversion for laser transition. Since the total relaxation rate \(\Gamma\) of the atomic dipole is at most on the order of \(\mathrm {10^{3} \, s^{-1}}\) and the cavity decay rate \(\kappa\) is \(\mathrm {9.4 \times 10^{5} \, s^{-1}}\), the cavity-pulling suppression factor is at least on the order of \(10^{3}\). Theoretical calculation shows laser linewidth can reach the mHz level. However, this result can only be achieved if the effective repump rate reaches \(\mathrm {10^{3} \, s^{-1}}\) and the atom number is at \(10^{6}\) level. Under this condition, the fluctuations in atomic transition frequency introduced due to AC Stark shift are negligible at mHz level. Moreover, the maximum laser output power is proportional to the square of the atom number. When the atom number is at \(10^{6}\), the power can reach pW order, enough to be used for the phase locking of a slave optical local oscillator.

Subsequently, the JILA group proposed the idea that using a high-finesse resonant cavity, based on alkaline-earth metal atoms with an ultra-narrow-linewidth transition to achieve a steady-state superradiance[88]. In order to obtain the intensity fluctuations of the steady-state superradiant laser, JILA performed an analysis using Monte Carlo simulations and semiclassical approximation methods [89]. They found that the light exhibits bunching below threshold, is to a good approximation coherent in the superradiant regime, and is chaotic above the second threshold. Toward achieving mHz linewidth, JILA studied superradiant lasing on the \(7.5 \,\textrm{kHz}\) linewidth dipole-forbidden \(\mathrm {^{3}P_{1}}\rightarrow \mathrm {^{1}S_{0}}\) transition at \(689 \,\textrm{nm}\), with an ensemble of \(^{88}\textrm{Sr}\) atoms tightly trapped in a \(1\textrm{D}\) optical lattice [76]. This laser is in a superradiant crossover regime, which means it can be operated at the crossover between good- and bad-cavity regimes. The cold-atom gain medium can be repumped to achieve quasi-steady-state lasing, and the frequency of the emitted light is determined by the atomic transition frequency when operated in the bad-cavity regime. They also characterized the cavity-pulling suppression of the bad cavity, where the laser frequency variation is reduced by an order of magnitude. Experimentally, the cavity-pulling coefficient is 0.09(2). They also obtained heterodyne power spectral density (PSD) between output light and 689 nm pump laser, with Lorentzian (Gaussian) full width at half maximum (FWHM) of 6.0(3) (4.7(3)) kHz. The measured linewidth is slightly narrower than the natural linewidth of the lasing transition (7.5 kHz) and far narrower than the linewidth imposed by repumping (100 kHz), exhibiting the linewidth-narrowing characteristic of synchronization in a laser.

Zhang et al. theoretically explained this linewidth-narrowing property [51]. When the ultracold \(^{88}\textrm{Sr}\) atoms in the optical lattice are exposed to a magnetic field, the ensemble of atoms with Zeeman-split excited states exhibits lasing with very narrow linewidth, which is orders of magnitude smaller than both the cavity linewidth and the incoherent atomic decay and excitation rates. The narrow-linewidth lasing is due to an interplay of multiatom superradiant effects and the coupling of bright and dark atom-light dressed states by the magnetic field. In 2018, the Department of Physics and Astronomy at Aarhus University theoretically analyzed \(^{87}\textrm{Sr}\) and \(^{88}\textrm{Sr}\) atoms also trapped within a one-dimensional optical lattice in a bad-cavity region [49]. Their calculations confirm that using \(\mathrm {^{3}P_{0}}\rightarrow \mathrm {^{1}S_{1}}\) of \(^{87}\textrm{Sr}\) atoms and \(\mathrm {^{3}P_{1}}\rightarrow \mathrm {^{1}S_{0}}\) of \(^{88}\textrm{Sr}\) atoms transitions, it is possible to realize the narrow linewidth of superradiant lasing. Specially, under strong driving of the dipole-forbidden transition \(\mathrm {^{3}P_{1}}\rightarrow \mathrm {^{1}S_{0}}\) of \(^{88}\textrm{Sr}\) atoms, the superradiant laser linewidth can be further narrowed due to the coherent excitation of the cavity field.

In 2014, Kazakov et al. discussed in detail two options for implementing active optical frequency standard: optical lattice AOC and atomic beam AOC. They analyzed some parameters required to achieve the best frequency stability as well as the implications and challenges in the implementation [90]. In addition, a “hybrid” method was proposed in which the atoms are prepared outside the cavity, fed into the cavity by a “guide beam” or “optical conveyors” to complete the stimulated radiation process. A blue-detuned optical lattice is used to prevent the atoms from moving along the cavity axis, suppressing decoherence and first-order Doppler effects. JILA has recently realized continuous loading of ultra-cold \(^{88}\textrm{Sr}\) atoms into a high-finesse ring cavity and using a moving optical lattice to transport the atoms along the cavity axis [78]. Experimentally, the loading rate reaches \(2.1(3)\times 10^{7}\) atoms/s. This work lays the foundation for the future implementation of continuous-type active superradiant lasers based on the mHz clock transition of \(^{87}\textrm{Sr}\) atom.

Aiming to achieve a CW AOC, the European Union (EU) has set up the iqClock project, led by the University of Amsterdam, in collaboration with six universities (University of Amsterdam, University of Birmingham, Nicolaus Copernicus University, University of Copenhagen, Vienna University of Technology, University of Innsbruck) and six companies (Teledyne e2v, TOPTICA, NKT Photonics, Acktar, Chronos Technology Ltd, British Telecom). A cold atomic beam scheme is used to achieve CW clock lasers by transporting Sr atoms through a moving optical lattice into a ring cavity. A clock laser linewidth of 100 mHz is expected to be achieved within 5 years and linewidth on the order of mHz within 10 years. In 2019, the University of Amsterdam realized a continuous guided atomic beam of \(^{88}\textrm{Sr}\) atoms with a phase-space density exceeding \(10^{-4}\) and a flux of \(3\times 10^{7}\) atoms/s [47]. With the optical guide, the atoms reach a velocity of 8.4 cm/s and can be used to complement the gain medium of the steady-state atom laser, which is an important step towards the realization of a steady-state superradiant AOC. In 2021, this group demonstrated a steady-state MOT of fermionic Sr atoms operating on the 7.5-kHz-wide \(^{1}\textrm{S}_{0}\)-\(^{3}\textrm{P}_{1}\) transition [48]. This MOT contains \(8.4\times 10^{7}\) atoms with a loading rate of \(1.3\times 10^{7}\) atoms/s and an average temperature of 12 \(\mathrm {\mu K}\), which can be used to provide a high flux of ultracold atoms source for the realization of a continuous superradiant AOC. Based on the steady-state MOT, this group has also achieved continuous Bose-Einstein condensation [91]. Through the magic wavelength optical conveyor in the ring cavity, a continuous source of ultracold Sr atoms in the excited state \(^{3}\textrm{P}_{0}\) can be realized, delivering several tens of millions of \(^{88}\textrm{Sr}\) atoms or millions of \(^{87}\textrm{Sr}\) atoms per second [82]. The use of the ring cavity increases the transfer speed, reduces atom losses and decreases the density of the atoms, paving the way for CW superradiant AOC.

3.2.2 Bad-cavity Raman three-level AOC

In 2012, JILA group proposed an bad-cavity Raman laser experimental scheme [42, 83], which achieved a Raman superradiant laser with an average photon number less than 0.2 in the cavity. Experimentally, the laser operates in deep bad-cavity region, where the ratio of the transverse decoherence rate to cavity decay rate of the laser transition is in the range of \(2 \times 10^{-5} \sim 10^{-3}\). About \(10^{6}\) \(^{87}\textrm{Rb}\) atoms are trapped by \(823 \,\textrm{nm}\) laser in one-dimensional optical lattice with a temperature of \(40 \,\mathrm {\mu K}\). The cavity is coupled to an optically dressed state that mimics a long-lived optically excited state. A \(795 \,\textrm{nm}\) linearly polarized dressing laser is applied to two magnetically insensitive energy levels to induce Raman transition. If the atoms are pumped continuously from ground state to metastable state while applying the dressing laser, a quasi-continuous superradiance laser with a duration of \(20-140 \, \textrm{ms}\) can be obtained. Each atom can radiate approximately 35 photons into the cavity mode. Under the action of light, collisions between atoms cause them to escape from the optical lattice, which eventually leads to a break in superradiance. The power spectrum (PSD) was obtained by heterodyning the superradiant laser and the dressing laser with a Gaussian FWHM of \(350 \,\textrm{Hz}\) and a Lorentzian FWHM of \(4.5 \,\textrm{Hz}\). Although this result is much narrower than the spontaneous radiation linewidth, it differs significantly from the theoretically calculated \(2(1) \,\textrm{mHz}\) linewidth due to the dispersion detuning of the cavity-mode frequency caused by atom number changing. In this experiment, a surprisingly tiny cavity-pulling coefficient \(P=4\times 10^{-5} \sim 2\times 10^{-3}\) is obtained, and it can be further enhanced by reducing decay rate \(\gamma\), which in turn suppresses the laser linewidth. Overall, this scheme proves the feasibility and superiority of AOC scheme, but there are problems of discontinuous output and weak power. The \(795 \,\textrm{nm}\) dressing laser and \(780 \,\textrm{nm}\) pump laser will introduce light shift, resulting in the bad-cavity Raman laser cannot be used as an optical frequency standard. To further achieve continuous superradiant laser, the decay rate of a single particle can be far balanced with the repumping rate by appropriate design so as to increase the laser cooling and trapping time.

Under this foundation, the JILA group investigated the oscillation relaxation, stability, and cavity feedback characteristics of the bad-cavity Raman superradiant laser [84]. Moreover, they demonstrated a hybrid mode in which the laser can switch between active sensing and passive phase measurements [85]. The results culminate in a hybrid sensor that combines active sensing of the collective atomic phase during superradiant emission with passive phase measurements using Ramsey-like evolution times, which are of guiding significance for the future development of ultra-narrow linewidth superradiant laser.

3.2.3 Ion trap three-level AOC

In 2014, the Peking University proposed an active ion optical clock scheme [86] using cold ions trapped in Paul trap as gain medium, which is expected to achieve active optical frequency standard with mHz linewidth. The basic principle of this scheme is similar to that of the optical lattice scheme, and theoretical studies have found that \(^{171}\textrm{Yb}^{+}\), \(^{191}\textrm{Hg}^{+}\), \(^{137,138}\textrm{Ba}^{+}\), \(^{43}\textrm{Ca}^{+}\), and \(^{87,88}\textrm{Sr}^{+}\) ions are suitable for active ion optical clock. Taking \(^{171}\textrm{Yb}^{+}\) as an example, the \(435.5 \,\textrm{nm}\) \(\mathrm {^{2}S_{1/2}}(F=0)-\mathrm {^{2}D_{3/2}}(F=1)\) transition with a natural linewidth of 3.1 Hz is chosen as clock laser. The cooling light and the repumping light correspond to \(369.5 \,\textrm{nm}\) \(\mathrm {^{2}S_{1/2}}(F=0)-\mathrm {^{2}P_{1/2}}(F=1)\) and \(\mathrm {^{2}S_{1/2}}(F=1)-\mathrm {^{2}P_{1/2}}(F=0)\) transitions, respectively, and both can be used for pumping ions to upper energy level \(\mathrm {^{2}D_{3/2}}(F=1,2)\). The ions at \(\mathrm {^{2}D_{3/2}}(F=2)\) are pumped to \(\mathrm {^{3}D_{1/2}}(F=1)\) by \(935 \,\textrm{nm}\) repumping laser. Eventually, most of the ions are transferred to \(\mathrm {^{2}D_{3/2}}(F=1)\) to achieve population inversion and stimulated radiation output. Theoretically, the laser output power can be up to \(37 \,\textrm{pW}\) when reaching steady state, and it can be increased to \(77 \,\textrm{pW}\) by increasing the light intensity and the ions number. However, it is difficult to significantly increase the ion number experimentally, and the ion AOC also suffers from the light shift caused by pumping laser, which ultimately affects the clock laser’s performance.

In 2017, Kazakov et al. proposed that a bad-cavity laser may be realized using forbidden transitions in large ensembles of cold ions that form a spherical Coulomb crystal in a linear Paul trap [45], which can guarantee longer trap lifetimes relative to neutral-atom-optical-lattice type. Micromotion-induced shifts such as the second-order Doppler and DC Stark shifts can be a suppressed by operating the ion trap at a magic frequency. Considering \(^{176}\textrm{Lu}^{+}\) ions imprisoned in a high finesse (\(\mathcal {F}=10^{5}\)) optical resonant cavity, an output power of 0.5 pW can be achieved based on the \(^{3}\textrm{D}_{2}\)-\(^{1}\textrm{S}_{0}\) transition when the ion number reaches \(10^{5}\) and the confinement frequency is 1 MHz [87]. If proper continuous cooling and pumping are provided, a truly steady-state AOC lasing in the bad-cavity regime is expected. This laser is promising to achieve an active optical frequency standard as a local oscillator for the next-generation optical clock scheme.

3.3 Four-level AOC

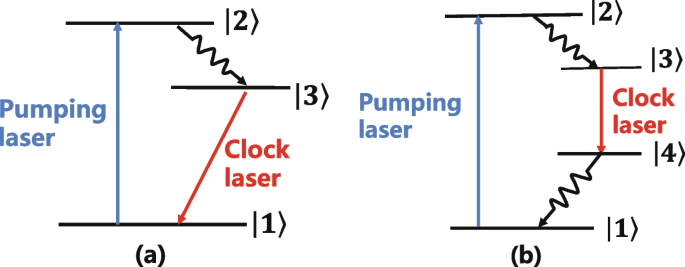
In the two-level atomic beam scheme, the Doppler effect of thermal atomic system is more influential. Using laser cooling technology can reduce the first-order Doppler effect, but this will complicate the system, and the residual Doppler effect will still limit the clock laser performance. The three-level optical lattice, Paul trap scheme for imprisoning atoms or ions is limited by light shift caused by pumping laser. Moreover, most of the above two schemes implement pulse AOC signals. In contrast, the four-level AOC scheme has three advantages. Firstly, the clock transition energy level does not involve the ground state, which can reduce light shift introduced by pumping laser. Secondly, a magnetic dipole transition energy level can be chosen, where the laser emission coefficient is not limited by smaller atom-cavity coupling constant compared to narrower linewidth electric dipole transition. Finally, the four-level AOC can be continuously pumped to output a stable CW AOC signal. Figure 4 shows the simplified energy level of the three- and four-level AOC schemes. In the three-level scheme, the light shift is inevitably introduced because the clock laser shares the ground state \(\vert 1\rangle\) with the pumping laser. Conversely, in the four-level scheme, atoms are pumped from ground state \(\vert 1\rangle\) to excited state \(\vert 2\rangle\). Due to spontaneous radiation, they are transferred to the clock transition upper energy level \(\vert 3\rangle\), where population inversion is formed between \(\vert 3\rangle\) and \(\vert 4\rangle\) to achieve stimulated radiation. Since the pumping laser and the clock laser transition energy levels are independent of each other, the light shift can be significantly reduced by choosing a suitable quantum system with a significant frequency difference.

In a four-level AOC scheme, the quantum system can select alkali metal atoms such as K [92], Rb [93, 94], and Cs [62, 95,96,97,98]. Taking Cs atom as an example, the Cs atomic gas cell is placed in a low-finesse optical cavity to make cavity-mode linewidth larger than gain linewidth to satisfy bad-cavity condition. Using a \(459\,\textrm{nm}\) laser as pumping laser, the Cs atoms are pumped from ground state \(\mathrm {6S_{1/2}}\) to the second excited state \(\mathrm {7P_{1/2}}\), then dropped to \(\mathrm {7S_{1/2}}\) state by spontaneous radiation, creating a population inversion between \(\mathrm {7S_{1/2}}\) and \(\mathrm {6P_{3/2}}\) when reaching steady state. Under the weak feedback of the optical cavity, the atomic dipoles are spontaneously synchronized with high coherence, producing a \(1470\,\textrm{nm}\) stimulated radiation clock laser. Different atoms and their corresponding energy level choices for four-level AOC are shown in Table 3.

3.3.1 Thermal atom four-level AOC

The four-energy level AOC scheme was first proposed by Yu et al. in 2010 [99].Theoretically, a superradiant laser with intensity proportional to \(N^{2}\) and linewidth scales to \(1/N^{2}\) is studied. In addition, the stationary state solution of full atomic cooperativity is derived, and the stability of the superradiant laser is analyzed under the assumption of no spontaneous radiation. Subsequently, Wang et al. carried out a related experiment based on the Cs atomic quantum system [100]. By measuring the intensity of fluorescence signals at different wavelengths, such as \(1470\,\textrm{nm}\) and \(1359\,\textrm{nm}\), they determined the formation of population inversion between clock transition energy levels. During the same period, a four-level scheme based on alkali metal K [92], Cs [95], and Rb [93] atoms was theoretically verified for feasibility based on the density matrix equation, and data such as the wavelength of the pumping laser and the energy level satisfying the population inversion were obtained. Moreover, the magic wavelengths corresponding to Rb atoms \(\mathrm {6S_{1/2}\rightarrow 5P_{1/2}}\) and \(\mathrm {6S_{1/2}\rightarrow 5P_{3/2}}\) were theoretically calculated in order to reduce the Doppler effect [101]. Using an optical lattice to imprison the laser-cooled atoms in the Lamb-Dick region, it is estimated that the effect of AC Stark frequency shift on the clock laser frequency stability can be reduced to less than \(10^{-18}\).

The AOC lasing at a wavelength of 1470 nm using the Cs four-level system was firstly achieved in 2013 [102]. On this basis, the \(1359\,\textrm{nm}\) and \(1470\,\textrm{nm}\) clock laser outputs were achieved successfully by using \(455\,\textrm{nm}\) and \(459\,\textrm{nm}\) pumping laser. The bad-cavity factor reached more than 40, and the \(1470\,\textrm{nm}\) laser linewidth reached \(407.3\,\textrm{Hz}\). For the Rb atom, a \(1367\,\textrm{nm}\) continuous active optical frequency standard was achieved using a \(420\,\textrm{nm}\) semiconductor laser with modulated transfer spectrum stabilization [94]. To further stabilize the resonant cavity length and reduce the frequency drift caused by the residual cavity-pulling effect, a dual-wavelength good-bad-cavity AOC is proposed [97]. In this scheme, two lasers of different wavelengths are output simultaneously in a common cavity and separately operate in good- and bad-cavity regions, called the good- and bad-cavity lasers. The good-cavity laser is locked to an ultra-stable cavity by the PDH technique to stabilize the cavity length. Therefore, as a clock laser, the bad-cavity laser will be further optimized due to the cavity-length stabilization with good-cavity laser. To reduce the impact of asynchronous cavity-length variation between two same systems on the linewidth broadening of the clock laser, the cavity-length stabilization was realized by utilizing the phase locking technique of good-cavity laser [62]. Experimentally, a 1470 nm CW active optical field with a few tens of Hz linewidth, four orders of magnitude below the natural linewidth of \(1.81\,\textrm{MHz}\), has been achieved at room temperature.

Based on Cs four-level AOC, Shi et al. proposed an anti-resonant laser [103], which is very different from the classical AOC operating in cavity resonance conditions. The lasing is realized when the atomic resonance is between two adjacent cavity resonances, that is, the cavity length equal to an odd multiple of a quarter wavelength. The linewidth of anti-resonant laser is not broadened compared to resonant laser, and its cavity-pulling suppression characteristic is stronger. Using this anti-resonant laser, the AOC can be extended from the cavity resonance region to the anti-resonance region, further improving the performance of the current active optical frequency standard.

3.3.2 Optical lattice four-level AOC

In order to solve the Doppler broadening problem in the four-level AOC based on thermal atoms, the Peking University, Guru Nanak Dev University, Beijing National Laboratory for Condensed Matter Physics, and the Indian Physical Research Laboratory calculated the magic wavelength corresponding to the \(1470\,\textrm{nm}\) Cs atom clock transition in detail [53]. The optical lattice four-level AOC scheme predicts output laser power up to \(24\,\mathrm {\mu W}\) with a \(\textrm{mHz}\) linewidth and a frequency uncertainty of \(2 \times 10^{-15}\). Singh et al. obtained the magic wavelengths between all possible hyperfine levels of the transitions in Rb and Cs atoms [60], which will help build a more stable AOC. They also gave the static dipole polarizabilities of Rb and Cs atoms to validate the results. Using cold atoms imprisoned in an optical lattice as the gain medium can reduce the gain linewidth broadening. In principle, an active optical frequency standard with a \(\textrm{mHz}\) linewidth, much smaller than the clock transition natural linewidth, can be obtained.

To sum up, the above two-, three-, and four-level AOC schemes all have advantages and disadvantages. The two-level structure is simple and easy to implement. However, its performance is ultimately limited by the second-order Doppler shift for the atomic beam and Faraday schemes, the pulsed mode operation and the \(\textrm{pW}\) laser power for the optical lattice scheme. Although the optical lattice three-level scheme can achieve higher performance using narrow linewidth quantum transition, it is not easy to realize experimentally due to the small atom number and weak output power. Moreover, the clock laser is ultimately limited by light shift. Because the pumping laser is separated from the clock laser, the four-level scheme avoids the light shift caused by the pumping laser. Moreover, the output laser is a continuous laser with a higher power which can reach approximately \(100 \, \mathrm {\mu W}\), but this scheme requires a higher atom number. The use of thermal atom gas cell can meet the corresponding atom number requirement. However, it is affected by the Doppler effect, which leads to a broadening of the gain profile. To further improve long-term stability, a cold-atom scheme can be used in the four-level scheme.

The applications of active optical frequency standards and clocks are wide ranging. Thanks to the development of atomic clocks, time and frequency are the most precise physical quantities that can be measured currently. As a result, tremendous advances in atomic clocks have made it possible to measure other physical and technical quantities that can be traced back to frequency with unprecedented precision. AOCs output an optical frequency standard directly based on the principle of stimulated radiation. Since it works in the bad-cavity region, which means the atomic gain linewidth is narrower than the cavity-mode linewidth, it can effectively solve the cavity-length thermal noise problem. Due to the phase coherence of collective dipole emission, the output laser has excellent phase coherence, which can exceed the quantum-limited linewidth determined by spontaneous emission. Thanks to the superior characteristics of the AOC, it can be used in a lot of fields, such as precision measurement, physical theory verification, gravitational detection, testing of quantum electrodynamics and so on.

4.1 Serves as a local oscillator for passive optical clocks

In order to detect the atomic transition spectrum with mHz linewidth, the linewidth of the local oscillator laser of a conventional passive optical clock must be narrow enough. At present, the ultra-narrow linewidth laser source is mainly obtained by the PDH technique. The use of ultra-stable cavities leads to expensive costs, complex systems, and environmental sensitivity. Moreover, it cannot solve the cavity-length thermal noise problem essentially. The narrow linewidth optical field based on the AOC scheme provides an excellent option to solve this problem. It can be used as the local oscillator laser for passive optical clocks. At the same time, this optical field has the absolute value characteristic of quantum transition frequency between atomic energy levels. Combined with the optical frequency synthesizer, we can realize the frequency comparison between the AOC and other high-precision optical clocks, thus realizing the transmission, comparison, and application of high-precision active quantum frequency standards. In the above cases, the AOC scheme will break through the technical bottleneck of the passive optical clock stability currently, which is limited by the cavity-length thermal noise. It can be applied to the definition of the second, the quantization of the International System of Units, the precision measurement of the gravitational potential, the verification of general relativity, the detection of dark matter, and other fields.

4.2 Application in precision spectroscopy

AOCs use the atomic stimulated radiation signal directly as the clock laser, whose output linewidth is narrower than the natural linewidth determined by spontaneous radiation. In terms of spectroscopy, it can be called stimulated radiation laser spectrum. Theoretically, the linewidth of this “stimulated radiation laser spectrum” is 7–8 orders of magnitude narrower than the natural linewidth of atomic transition. Therefore, narrow linewidth CW AOC can provide new principles and methods for precision atomic spectroscopy. For example, the Peking University has been able to accurately measure the 1470 nm transition line (natural linewidth \(\sim\) 1.81 MHz [104]) to the Hz level using the Cs four-level AOC scheme[62], which is 5–6 orders of magnitude more accurate than the previous 1470 nm spectral line measurement. This method can also be universally extended to other alkali metal atoms, realizing the high-precision measurement of transition spectral lines with MHz natural linewidths, which is expected to be upgraded to the measurement accuracy based on conventional optical clocks. In this way, the new principle and technology of the AOC can enrich the international high-precision spectral measurements and improve the measurement precision of atomic spectroscopy with MHz natural linewidths.

4.3 Hyperfine-structure measurement

In the work of Shi et al.[105], the Cs atomic four-level AOC can be used not only to realize narrow linewidth active optical frequency standard but also to realize the hyperfine level measurement of Cs \(7\mathrm {P_{1/2}}\) in combination with the Doppler effect. Since the AOC uses quantum reference system stimulated radiation directly as the clock transition signal, the output linewidth is much smaller than the natural linewidth determined by spontaneous radiation, which can improve the measurement accuracy of atomic hyperfine level structure constants.

The experimental principle is similar to that of the Cs four-level AOC, where the \(459\,\textrm{nm}\) pumping laser is locked to \(\mathrm {6S_{1/2}}(F=4)\rightarrow \mathrm {7P_{1/2}}(F^{\prime }=3 \& 4)\) by modulation transfer spectrum. The Cs atoms in the atomic gas cell are thermal atoms with Doppler velocity distribution, and the Cs atoms in different velocity groups in the cavity sense different pumping laser frequencies. According to the selection rule, the Cs atoms located in the two velocity groups of the \(\mathrm {6S_{1/2}}(F=4)\)state can be excited to \(\mathrm {7P_{1/2}}(F^{\prime }=3)\) and \(\mathrm {7P_{1/2}}(F^{\prime }=4)\), respectively. Cs atoms propagate with the pumping laser with velocity \(v_{1} = \lambda _{459.3\,\textrm{nm}} \times \Delta \nu /2\) are sensed at pumping laser frequency corresponding to \(\mathrm {6S_{1/2}}(F=4)-\mathrm {7P_{1/2}}(F^{\prime }=3)\). Conversely, when Cs atoms counter-propagate with the pumping laser with velocity \(v_{2} = -\lambda _{459.3\,\textrm{nm}} \times \Delta \nu /2\) are pumped to \(\mathrm {7P_{1/2}}(F^{\prime }=4)\), where \(\Delta \nu\) is the hyperfine level spacing of the \(7P_{1/2}\) state. Atoms pumped to both \(\mathrm {7P_{1/2}}(F^{\prime }=3)\) and \(\mathrm {7P_{1/2}}(F^{\prime }=4)\) can drop to \(\mathrm {7S_{1/2}}(F^{\prime \prime }=4)\) through spontaneous radiation, creating a population inversion between \(\mathrm {7S_{1/2}}\) and \(\mathrm {6P_{3/2}}\). Eventually, the atoms of both velocity groups can output \(1470\,\textrm{nm}\) bad-cavity clock laser corresponding to \(\mathrm {7S_{1/2}}(F^{\prime \prime }=4)-\mathrm {6P_{3/2}}(F^{\prime \prime \prime }=5)\). The frequency difference \(\Delta f\) of the stimulated emission lights of atoms with two velocity groups can be measured by optical heterodyne, where \(\Delta f=\frac{\lambda _{459.3 \,\mathrm {~m}}}{\lambda _{1469.9 \,\textrm{nm}}} \times \Delta \nu\). The hyperfine level spacing \(\Delta \nu\) of the \(\mathrm {7P_{1/2}}\) state can be deduced from the experimentally measured \(\Delta f\), and then the magnetic dipole hyperfine constant A of \(7\textrm{P}_{1/2}\) state can be found using \(\Delta \nu = A \times 4\).

The scheme uses one system for measurement, which can eliminate common mode noise, but is limited by the cavity-pulling effect. Considering the errors introduced by the cavity-pulling effect, the measurement result is \(\Delta f=118.0347 \pm 0.1827\,\textrm{MHz}\). Hence, the hyperfine level spacing of the \(7\mathrm {P_{1/2}}\) state is \(377.628 \pm 0.584\,\textrm{MHz}\), and the magnetic dipole hyperfine constant is \(94.41(15)\,\textrm{MHz}\). Data comparison shows that this work’s result is in general agreement with those obtained previously using saturated absorption spectroscopy and two-photon resonance spectroscopy.

4.4 Magnetometer based on bad-cavity Raman AOC superradiant laser

Most atomic magnetometers pass probe light through atomic vapor and sense the response of the atom to magnetic field by measuring the polarization rotation or phase shift of the probe light. In Ref. [106], a Raman laser magnetometer based on cold atom superradiant was demonstrated, where the phase of stimulated radiation was directly detected to identify the phase response of atomic dipole to external magnetic field. This experiment implemented a magnetometer using active mapping of atomic phase to optical field phase that can operate in both active and passive field sensing modes. Unlike typical good-cavity lasers, this laser can be operated in the bad-cavity region. Since the atomic gain medium is the primary reservoir of phase information, a passive oscillation mode is possible in this bad-cavity laser. The sensor can dynamically selectively switch between active oscillation and passive Ramsey-like phase evolution. This flexibility is achieved by controlling the optical radiation rate of atomic dipole via the intensity of Raman dressing laser.

Based on previous experiments, \(10^{6}\) \(^{87}\textrm{Rb}\) atoms were imprisoned in a one-dimensional optical lattice after laser cooling to \(40 \,\mathrm {\mu K}\). The volume of the atom cloud is roughly \(2.1\times 10^{-3} \,\mathrm {mm^{3}}\) using a low-finesse (\(\mathcal {F}=710\)) resonant cavity. The atoms are continuously pumped to \(\mathrm {5^{2}S_{1/2} }(F=2, m_{F}=2)\) and decay to \(\mathrm {5^{2}S_{1/2} }(F=1, m_{F}=1)\) through Raman transition. Using these two magnetic field-sensitive states, the pseudospin 1/2 regime is formed. The states sensitive to the magnetic field are chosen instead of the cavity resonant frequency, because the laser operates in bad-cavity region with cavity-pulling suppression effect. Experimentally, the wideband sensitivity at continuous active oscillation was measured, and the narrowband sensitivity in a passive Ramsay-like mode was obtained by narrowband detection using the spin-echo technique. Its sensitivity reaches \(190\,\mathrm {pT/\sqrt{Hz}}\) at \(1\,\textrm{kHz}\), and the effective detection volume, which is the volume of the atomic cloud, is about \(2\times 10^{-3} \,\mathrm {mm^{3}}\). Future experimental work will focus on achieving truly continuous operation and realizing sensitivity at the phase diffusion limit.

The AOC, which is based on the principle of stimulated radiation, its output signal has excellent phase coherence and can be used directly as an optical frequency standard. Working in the bad-cavity region, where the atomic gain linewidth is narrower than the cavity-mode linewidth, the AOC can effectively solve the cavity-length thermal noise problem in passive optical clocks. We describe in detail the basic principles and characteristics of AOC and classify AOC into two-, three-, and four-level schemes according to the energy-level structure of atoms for stimulated radiation. Currently, the two-level scheme includes atomic beam, Faraday atomic filter, and optical lattice type; the three-level scheme includes optical lattice, bad-cavity Raman, and ion trapping type; the four-level scheme includes thermal atom and optical-lattice-trapped cold atom type. It is worth noting that there are schemes that combine atomic beam and optical lattice to achieve CW AOCs. For different energy levels, international research progress is introduced in detail, including JILA, NIST research group, iqClock program in the EU, Peking University, Vienna University of Technology, University of Copenhagen, Aarhus University, and Physical Research Laboratory (India).

Almost 20 years have passed since AOC was proposed in 2005. During this period, the AOC has extensively developed. However, where should AOC goes in the future? The basic direction is still to continue to improve the inaccuracy and stability of the AOC to make it closer to the theoretical expectation. As the performance of the AOC improves, it is expected to achieve higher precision measurement in gravitational wave detection, general relativity verification, searching for time variation of fundamental constants, detection of dark matter, and so on. In addition to the above frontier scientific research, it can also be applied to satellite navigation and positioning, gravitational potential detection, the provision of the SI unit of time, etc. Several research groups are currently working to solve the challenge of the pulsed output mode of the AOC, viewing to achieve continuous clock laser. Besides, the automation, miniaturization, and transportability of the AOC are also worth exploring. Although there are still many challenges, there is no doubt that AOCs will make a more significant impact on science and technology in the future.