1 Introduction

In the past decade, the development of integrated electronic circuits characterized by Moore’s law has slowed down, and various forms of non-silicon physical computing have been highly anticipated [1,2,3,4]. Unlike digital computers of von Neumann architecture, computers in non-silicon forms take the task of simulating physical systems., such as superconducting quantum computers [5,6,7,8], quantum annealers [9, 10], physical neural networks [3], and coherent Ising machines (CIMs) [11,12,13]. Among them, CIMs have been extensively studied due to their excellent performance on combinatorial optimization problems and have been implemented by various physical systems, such as optics [11,12,13], nanomagnetic-net arrays [14, 15], single-atom [16], and complementary oxide semiconductor devices [17].

The combinatorial optimization problem requires finding an optimal solution that minimizes the loss function among the combinations of all options, which belongs to the non-deterministic polynomial time (NP)-hard problem. There are many combinatorial optimization problems in various important domains, such as financial portfolios [18], drug discovery [19], integrated circuit design [20], and Max-Cut problems [21]. Ising models are mathematical abstractions of spin glasses that describe disordered magnetic systems. The Hamiltonian of Ising machine could be expressed as \(H_\mathrm{Ising}=-\sum \limits _{i,j}J_{ij}\sigma_i\sigma_j\), where \(J_{ij}\) denote the coupling coefficients between the i th and j th spins and \(\sigma _i\in \{-1,1\}\). The Max-Cut problem is equivalent to searching for the ground state energy of an Ising model [21]

\(\begin{aligned} Edges = \frac{1}{4}\left( \sum \limits _{i,j}J_{ij}-\sum \limits _{i,j}J_{ij}\sigma _{i}\sigma _{j}\right) . \end{aligned} \)
(1)

Therefore, the solution of the ground states of the Ising model is also an NP-hard problem.

Quantum computers should be able to simulate quantum systems more efficiently than classical computers [22, 23], but achieving large-scale quantum computers is still challenging at this stage. Many approximation algorithms, such as Monte Carlo-based simulated annealing, can be applied to solve these combinatorial optimization problems. However, the solution time increases exponentially on conventional computers depending on the scale of the problem [24]. Therefore, it is necessary to consider whether physical simulators can be used to replace traditional computers. Therefore, the CIM hardware solver is the best choice for implementing a physical simulator to solve combinatorial optimization problems [25].

The noise of squeezed states exhibits the squeezing and anti-squeezing of the quadratures in the orthogonal components through nonlinear effects, respectively. The squeezed light that anti-squeezed in-phase noise can help us to realize CIM with a quantum parallel search process. As a hardware solver, the experimentally demonstrated excellent performance of CIM in combinatorial optimization has aroused extensive research interests [11, 12, 26]. In this brief review, we focus on the recent progress of squeezed-light-based CIMs, comparing their differences and the unique advantages of their special structures. The main structure of the review is as follows: Section 2 mainly introduces the principle and optical implementation of degenerate optical parametric oscillator (DOPO)-based CIM. Section 3 summarizes some challenges to be solved. We believe this review can provide a reference for CIM research in the future.

2 Coherent Ising machines based on squeezed states

Photons have been seen as a good medium for computing and are often used in the field of quantum computing [27,28,29] due to their inherent advantages in information processing, such as highly parallel computing due to no interference between different bands [2, 30,31,32,33,34], wide bandwidth from additional orbital angular momentum and polarization [35, 36, 36, 37], and low loss over long distances [38, 39].

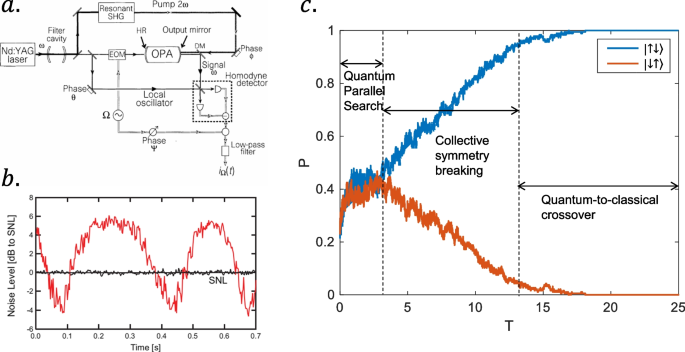
Compared with coherent light, the squeezed vacuum state of light has reduced uncertainty in a specific quadrature and can be widely used in quantum information processing [40,41,42], gravitational wave detection 43, 44], quantum sensing [45,46,47], and optical parametric amplification [48]. Figure 1a [48] shows an experimental scheme for generating squeezed light. The experiment produces squeezed noise below the shot noise limit and anti-squeezed noise above the shot noise limit, as shown in Fig. 1b [49]. Noise above the shot noise limit helps CIM to achieve the quantum parallel search.

Fig. 1
figure 1

Experimental scheme for generating squeezed light. a Experimental scheme for generating bright squeezed light and squeezed vacuum with an optical parametric oscillator (OPA). EOM, electro-optic modulator; DM, dichroic mirror; SHG, second harmonic generator; HR, high reflector. Figure 1a reproduced from Ref. [ 48] with permission of the Springer Nature. b Typical vacuum squeezing noise measurement (red) compared to the shot-noise limit (black). Figure  1b reproduced from Ref. [ 49] with permission of the American Physical Society. c The anti-ferromagnetic computing process of CIM (N = 2) and the success rate of finding two degenerate ground states varies with time


In addition, the mutual injection between the optical pulse networks can simulate the interaction relationship in the Ising model. Therefore, squeezed light implementation of CIM based on degenerate optical parametric oscillator (DOPO) is an effective way. We present a calculation process of CIM based on a degenerate parametric oscillator in anti-ferromagnetic 2-spin by numerical simulation in Fig.  1c. The probabilities of both degenerate ground states \((|{\uparrow \downarrow }\rangle\) and \(|{\downarrow \uparrow }\rangle )\) at the beginning of the calculation are both rising under the influence of noise until the collective symmetry-breaking stage. Then, the system randomly selects a ground state, and a quantum-to-classical crossover occurs. Recently, the experimental progress of the optical CIM has been listed as follows.

2.1 CIM based on DOPO

The Ising model is used to simulate the random process of the phase transition of matter. It is a binary spin system, and each bit is randomly flipped under the influence of the potential energy field [50]. Therefore, the artificially analog spin in the Ising machine that simulates the evolution of the Ising model should also have this property. Coincidentally, such a binary value occurs when the evolution of nonlinear dynamics satisfies \(\dot{x}=\alpha x-x^3\). Nonlinear optics, which has been widely studied in optical frequency combs [51, 52], optomechanics [53, 54], squeezed light [48, 55, 56], and optical frequency conversion [57,58,59]. Wang Zhe et al. proposed that CIM can be implemented using optical parametric oscillators (OPO) [21].

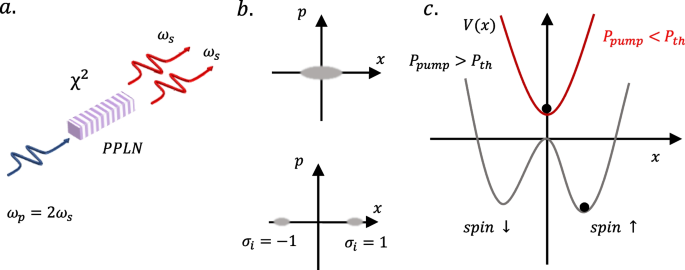
Optical parametric oscillation (OPO) describes the nonlinear optical process that converts a high-energy photon into two low-energy photons through \(\chi ^{(2)}\) nonlinear crystals [60,61,62,63,64,65,66], as shown in Fig. 2a. OPO is an open dissipative system with a second-order phase transition at the oscillation threshold, with gain competition among the multiple modes in the laser [67]. Moreover, it has been experimentally proved that an Ising Hamiltonian can be simulated in a mutual injection-locked laser network [68]. A DOPO, under coherent excitation \(\hat{H}_d=i\hbar \epsilon (\hat{a}_p^{\dagger }e^{-i\omega _dt}-\hat{a}_pe^{i\omega _dt})\), the interacting Hamiltonian is \(\hat{H}_{int}=i\hbar \frac{\kappa }{2} (\hat{a}_s^{\dagger 2}\hat{a}_p-\hat{a}_s^{2}\hat{a}_p^{\dagger })\), and \(\hat{a}_p(\hat{a}_s)\) is the pump (signal) mode. Considering the linear dissipation of the pump (signal) mode as \(\gamma _p(\gamma _s)\), the Heisenberg-Langevin equations of the system are [69]

\(\begin{aligned} \frac{d\hat{a}_p}{dt}= & {} \epsilon -\gamma _p\hat{a}_p-\frac{\kappa }{2}\hat{a}_s^{2}+\sqrt{\gamma _p}\hat{F}_1,\nonumber \\ \frac{d\hat{a}_s}{dt}= & {} -\gamma _s\hat{a}_s-\frac{\kappa }{2}\hat{a}_s^{\dagger }\hat{a}_p+\sqrt{\gamma _s}\hat{F}_2,. \end{aligned}\)
(2)

Fig. 2
figure 2

Schematic diagram of the analog spin system based on DOPO. a DOPO process. A high-energy photon (indicated in blue) incident on the PPLN crystal is converted into two identical low-energy photons (indicated in red). PPLN: Periodically polarized lithium niobate crystal. b Quantum noise distribution of DOPO, b is below the threshold, and c is above the threshold. d The trend of the potential function does not oscillate below the threshold (red) and a bistable potential above the threshold (gray line). The pump energy rises, and the analog spin selects a state with lower potential energy


Here, \(\hat{F}_{1(2)}\) is the time-dependent noise operators for the pump (signal) field, and \(\left\langle \hat{F}_i(t)\hat{F}_j^{\dagger }(t')\right\rangle =\delta _{ij}\delta {(t-t')}\). When \(\gamma _p\) is large, we can adiabatically eliminate the pump operator \(\hat{a}_p\) by \(d\hat{a}_p/dt=0\). Therefore, the Heisenberg-Langevin equation for the signal mode becomes

\(\begin{aligned} \frac{d\hat{a}_s}{dt}=-\gamma _s\hat{a}_s+R\hat{a}_s^{\dagger }-K\hat{a}_s^{\dagger }\hat{a}_s^2+\sqrt{2K}\hat{a}_s^{\dagger }\hat{F}_1+\sqrt{\gamma _s}\hat{F}_2. \end{aligned}\)
(3)

Here, \(R=\kappa \epsilon /\gamma _p\) is gain coefficient and \(K=\kappa ^2/(2\gamma _p)\) is saturation coefficient. Its equivalent master equation is [69]

\(\begin{aligned} \frac{d\hat{\rho }}{dt}= & {} \gamma _s\left( \left[ \hat{a}_s,\rho \hat{a}_s^{\dagger }\right] +H.c.\right) +p\frac{\gamma _s}{2}\left[ \hat{a}_s^{\dagger 2}-\hat{a}_s^{2},\hat{\rho }\right] \nonumber \\{} & {} +g^2\frac{\gamma _s}{2}\left[ \hat{a}_s^{2},\hat{\rho }\hat{a}_s^{\dagger 2}+H.c.\right] . \end{aligned}\)
(4)

where parametric gain \(p=K/\gamma _s\), and two-photon absorption coefficient is \(g^2=R/\gamma _s\). Then, we extend the total field density operator \(\rho\) using the positive-P representation \(P(\alpha ,\beta )\) and get the Fock-Planck equation [70]. We ignore the third- and higher-order terms of the Fock-Planck equation and obtain the c-number SDEs of \(i-th\) DOPO by the Ito rules

\(\begin{aligned} \frac{d\alpha _i}{dt}= & {} -\alpha _i+p\beta _i-g^2\beta _i\alpha _i^2+\sqrt{p-g^2\alpha _i^2}\hat{f}_{i,\alpha },\nonumber \\ \frac{d\beta _i}{dt}= & {} -\beta _i+p\alpha _i-g^2\beta _i^2\alpha _i+\sqrt{p-g^2\beta _i^2}\hat{f}_{i,\beta }. \end{aligned}\)
(5)

Here, \(\hat{f}_{i,\alpha (\beta )}\) is real random noise number and \(\left\langle \hat{f}_{i,a}(t)\hat{f}_{j,b}^{\dagger }(t')\right\rangle =\delta _{ij}\delta _{ab}\delta {(t-t')}\). Under the positive-P representation, \(\alpha ,\beta\) is generally a complex number, but the parametric oscillations ensure that \(\alpha ,\beta\) can be restricted to real numbers [21]. By ignoring the quantum noise term, the amplitude evolution of the ith DOPO can be expressed as

\(\begin{aligned} \frac{d\mu _i}{dt}=(p-1)\mu _i-\mu _i^3+\sum \limits ^N\limits _{j=1,j\ne i}\varepsilon J_{ij}\mu _j. \end{aligned}\)
(6)

Here, \(\mu _i\) is the amplitude of i th DOPO pulse, and \(\varepsilon\) is the coupling strength between pulses. The evolution of the amplitude of DOPO satisfies \(\dot{\mu }=-\frac{dV(\mu )}{d\mu }\), and \(V(\mu )=(1-p)\mu ^2/2+\mu ^4/4\) is the potential function [ 71]. The evolution of DOPO is shown in Fig.  2b and c. Below the pump threshold, the pulses are amplified and unamplified in the \(x-\)axis and \(p-\)axis in a squeezed vacuum state. When the parametric oscillation gain is greater than the dissipation of the cavity, the pulse can have a stable non-zero amplitude on the x-axis. However, the probability of selecting phase 0 or phase \(\pi\) is 50% each. This phenomenon is the collective symmetry breaking [ 72].

In addition, the relationship between V(x) and the pump threshold is given in Fig.  2d. The system is only stable near the amplitude zero point when the pump intensity is below the oscillation threshold. Moreover, by increasing pump intensity to the oscillation threshold, the potential energy of the system becomes a paradigmatic bistable potential. The system chooses positive amplitude or negative amplitude with equal probability. By adjusting the pump gain, the existence of the coupling term makes the depth of the potential difference. The system will select the ground state with lower energy, the optimal spin configuration, which is the operating principle of CIM [ 73]. The CIM based on DOPO has been proven to have excellent performance in dealing with combinatorial optimization problems, such as Max-Cut, in numerical simulation [ 21].

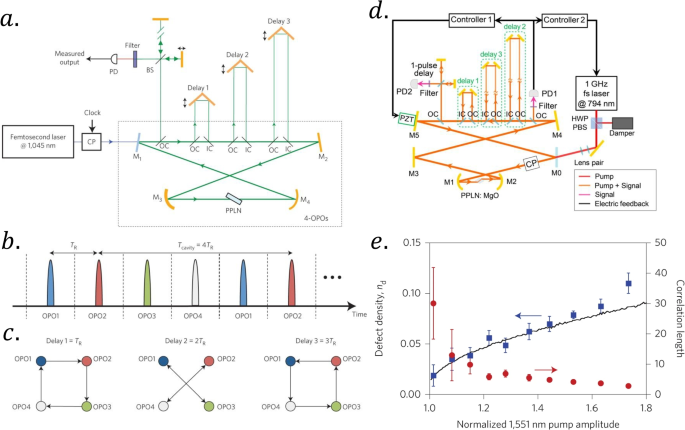
Based on DOPO, these schemes successfully implement a CIM, which implements the coupling between different pulses through a delayed optical path [73,74,75]. The earliest scheme shown in Fig. 3a to implement optical CIM is based on a femtosecond laser-driven DOPO [73]. A fixed-length delay optical path can implement different pulse couplings, and different coupling structures can be implemented by different length delay optical paths, as shown in Fig. 3c. Later, the scheme was extended to the 16-spin system to solve the more complex combinatorial optimization problem, as shown in Fig. 3d. T. Inagaki et al. used a 10,000-OPO CIM to simulate a 1D anti-ferromagnetic Ising chain. They observed the formation of spin domains in Fig. 3e, indicating that the DOPO network can simulate the behavior of low-temperature Ising spins [75].

Fig. 3
figure 3

Example of CIM based on DOPO. a Schematic diagram of 4-OPO composition coherent Ising machine from Ref. [ 73]. b The interval of the output OPO pulse and the coupling of the injection optical path is realized at c, from Ref. [ 73]. Figure 3a, b and c reproduced from Ref. [ 73] with permission of the Springer Nature. d Schematic diagram of 16-OPO composition coherent Ising machine reproduced from Ref. [ 74] with permission of the Springer Nature. e 1D Ising model simulation observed defect density \(n_d\) and correlation length \(x_0\) as a function of normalized 1551 nm pump amplitude reproduced from Ref. [ 75] with permission of the Springer Nature


In addition, the optical CIM provides a new solution to the combinatorial optimization problem and a reference for other ways to implement CIM.

2.2 CIM based on the measurement feed-back

Although the optical CIM based on the optical delay path performs well in some of these optimization problems, the fixed-length delay optical path can only map the combinatorial optimization problem with a single structure [ 74]. However, the combinatorial optimization problem is complex, and the CIM that can be connected arbitrarily becomes a new challenge.

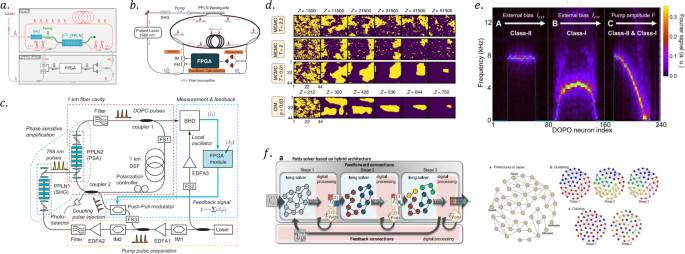
Therefore, a measurement feedback system (MFB) is proposed by first measuring the pulse amplitude and then modulating the pulse through the optical modulator and injecting it into the target pulse at the appropriate time [11, 12]. CIM with MFB adds a field programmable gate array (FPGA) based on the DOPO fiber-ring cavity and implements the measurement-calculation-feedback process through FPGA [26], as shown in Fig. 4a. McMahon P. L. et al. first implemented a fully programmable optical CIM that can easily map arbitrarily connected Ising models, even including the case of asymmetric coupling \(J_{ij}\ne J_{ji}\) [11], as shown in Fig. 4b. CIM with MFB is implemented by taking parts (\(10\%\)) of each pulse for measurement and then feedback injection. The machine can find exact solutions, or good approximate solutions, to various difficult combinatorial optimization problems under 100-spins. In Fig. 4c, the scheme has been extended to 2000-spins to solve more complex combinatorial optimization problems by increasing the fiber loop length and the firing rate of the pulses [12]. The experimental results show that the machine can achieve the same calculation result in 1% of the time of the simulated annealing (SA) implemented in the state-of-the-art central processing unit (CPU), showing the accelerated calculation effect of optical CIM [12]. The latest research about 100,000-spins CIM shows that by optimizing the parallel FPGA, the computation time of CIM with MFB only depends on the time which the light pulse runs in the fiber-ring [79].

Fig. 4
figure 4

Example of CIM with MFB and applications. a The schematic diagram of CIM with MFB reproduced from Ref. [ 26] with permission of the American Association for the Advancement of Science. b 100-spin CIM realizes full connection reproduced from Ref. [ 11] with permission of the American Association for the Advancement of Science. c 2000-spin CIM machines for solving combinatorial optimization problems reproduced from Ref. [ 12] with permission of the American Association for the Advancement of Science. d CIM simulation of 2D Ising problem evolution versus low-temperature Monte Carlo simulation reproduced from Ref. [ 76] with permission of the Springer Nature. e CIM to simulate spiking neuron dynamics reproduced from Ref. [ 77] with permission of the Springer Nature. f CIM simulates the Potts model schematic and solves the clustering and coloring problems reproduced from Ref. [ 78] with permission of the Springer Nature.


CIM with MFB shows computational performance advantages over current digital computer [80,81,82]. R. Hamerly et al. also compared the performance of CIM with MFB and quantum annealer. They found that CIM with MFB is weaker than quantum annealer in the calculation of simple graphs (sparse) while having obvious advantages over quantum annealer in more complex graphs (dense) [26]. Furthermore, to understand the evolution process of CIM searching for the ground state, F. Böhm et al. used CIM with MFB to simulate the evolution process of 2D anti-ferromagnetic Ising networks. They found that CIMs behave like low-temperature spin systems, making them suitable for solving combinatorial optimization tasks, as shown in Fig. 4d [76]. Spiking neurons, specialized neurons that process signals in human brain, have been shown to have better computing performance than traditional artificial neurons and are regarded as the next computational neural network [83, 84]. T. Inagaki et al. studied the dynamic behavior of spiking neurons in neural clusters simulated by CIM. They found that it helps to improve the computational performance of CIM, as shown in Fig. 4e [77]. CIM is also considered to be able to simulate the Potts model of multi-valued spins, as shown in Fig. 4f [78], and it is shown, through experiments, that clustering and coloring problems can be achieved.

3 Discussion and outlook

The optically implemented CIM shows the advantages of physical simulation machines in simulating physical systems. This novel form of optical computing provides a way to develop new computer structures, but there are also potential challenges that we need to address.

Large-scale CIM based on DOPO networks needs to increase the spin scale by increasing the length of the fiber-ring cavity or increasing the pump repetition rate. However, the nonlinear and thermal effects of long-distance optical fibers will bring instability to the system [79]. How to achieve high stability under large-scale requirements is a challenge. In addition, the study on improving the performance of CIM hardware solver improvement has been widely existed [85, 86]. Moreover, what role quantum noise and thermal noise play in the calculation process of CIM and how to improve the CIM hardware solver to improve performance will also be interesting questions.

Moreover, the CIM-inspired algorithm combined with the FPGA-implemented machine also showed excellent computational performance in solving combinatorial optimization problems, even better than optical CIM [87, 88]. Implementing CIM with better computing performance is also a challenge for simulating quantum systems using a physical system.

The introduction of nonlinear filtering to CIM reduces amplitude heterogeneity [89,90,91]. Also, it connects CIM with quantum neural networks and quantum perceptrons due to the wide application of nonlinear functions in artificial intelligence. The neural network and quantum perceptron based on the time multiplexing optical fiber-ring of CIM is worth looking forward to [92, 93]. For example, the spiking neural network has been simulated in CIM [77]. Meanwhile, CIMs based on nonlinear optics are also expected to promote the research of nonlinear optics due to their fully connected properties and system scalability.

In summary, we review the CIM based on squeezed light in this brief review, summarizing the advantages, challenges, and potential applications of the existing schemes. Combined with the recent rapid development of electro-optic modulators and photonic chips [94,95,96], it is reasonable to expect CIMs with better computing performance.