AAPPS bulletin

Research and Review

Squeezing for cosmic symphony

writerMengyao Wang & Fan Zhang

Vol.33 (Feb) 2023 | Article no.5 2023

Abstract

We briefly review the status of applying quantum squeezing to aid the search for gravitational waves with km-scale laser interferometers operating in the audio frequency band. The target audience is quantum optics professionals who are interested in an easily accessible introduction to the gravitational wave detector, both as an application of squeezing and as a platform for developing other quantum techniques.

1 Background and introduction

One of the main thrusts of modern theoretical physics is to achieve the matrimony between quantum mechanics and general relativity. This is an exceedingly difficult task, and the success is possibly decades away, yet the matchmakers may well take some solace, in the fact that at least within the realm of experimental gravitational wave detection, quantum techniques have shown great potential in aiding the detection of one of relativity’s prominent predictions. Perhaps the most readily attainable in this respect is the adoption of the squeezing of photons, that alters the characteristics of the inherent quantum uncertainty to suppress the associated noises. Photons are particularly amenable to quantum manipulations, because within the old school terminology of first and second quantizations, the familiar Maxwellian electromagnetic field, allowing for wave solutions of arbitrary wavelength, can already be seen as the first quantized wave function for photons. Subsequently, in contrast to massive particles that hide their quantum innards within highly localized microscopic packets, photons spread out closer to the scale of macroscopic apparatus. It is thus to nobody’s surprise that squeezing, amongst other quantum optics wizardry, underlies much of quantum technology developments [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. In this brief review, we share our excitement about the prospect of applying squeezing to gravitational wave detection, beginning with some quick background introductions.

1.1 Gravitational waves

As soon as one writes down the expression \(ma = GMm/r^2\) for Newtonian gravity, one realizes that there is something unusual. The analogous expression for the Coulomb force \(ma = \kappa q_1 q_2/r^2\) does not admit a cancelation between the inertial mass and the charge for the force. The result is that with electromagnetism, one can easily tell if there is an electric field present, by simply enlisting two equal mass but differently charged particles and observing if there is a differential in their acceleration. For gravity in contrast, such a strategy fails as the aforementioned cancelation removes all dependence on the specifics of the test particles, so the two particles always fall in synchronization. Subsequently, we can never tell if their observed acceleration is due to the presence of a gravitational field or that we are in an accelerating reference elevator. Generalizing this musing to all possible experiments, we arrive at the equivalence principle.

Physics is an experimental science, so if no experiments can tell apart a gravitational field and an accelerating reference frame, they should be regarded as being the same. Thus, gravity is not a force, and freely falling objects should follow “straight lines” in the sense of taking the shortest paths possible as per Newton’s first law. However, gravity is not without impact. Going into the next level of details and considering a setup where the gravitational field is not uniform, e.g., around Earth where the field always points towards the center and thus not parallel, then freely falling objects with initially parallel velocities will turn gradually to head towards the center and hit each other if they started close together. We are thus presented with the situation where initially parallel “straight lines” must be able to cross each other. Only non-Euclidean geometry admits such oddity; thus, gravity represents a warping of spacetime. The equivalence principle can now be understood geometrically: in a small region wherein the gravitational field does not change significantly, the curved spacetime is indistinguishable from its flat tangent plane. On the other hand, if we zoom out to a larger scale on which the gravitational field appreciably vary, we notice that the spacetime is actually curved.

Such warping can beFootnote 1 sourced by matter as per our usual intuition with gravity and must be consistent with special relativity, so any information regarding changes to the matter source must propagate out at a finite speed capped by the speed of light. We have thus a situation akin to electromagnetism, whereby the electromagnetic waves act as the messenger, informing Coulomb field lines far afield if a charge suddenly jerks around and settles to a new location, so they can all change to form a new spoke pattern now centered on the new charge position. In the case of gravity, the messenger is the gravitational wave. Gravity or warping of spacetime is described by a (Riemann) tensor with four indices, in contrast to the electromagnetic field tensor with two indices, so it is not surprising that its analog to the electric field tensor, called the tidal tensor, is represented by a traceless matrix at each location. It describes the variations in strength of gravity across spatial locations and tends to stretch and squeeze things, just like the variation of the Moon’s gravity causes tides on Earth, thus the name.

Similar to the electric field being orthogonal to the propagation direction of an electromagnetic waveFootnote 2, the only nonvanishing eigenvalues for the tidal tensor of a gravitational wave correspond to two eigenvectors perpendicular to the propagation direction and must add up to zero since the tidal tensor is traceless. Such a configuration describes tidal stretching along one of the eigenvetor directions, being equaled in strength (proportional to the eigenvalue) to a squashing along the other (orthogonal) eigenvector direction [15]. Such contortions are physical, in the sense that the r in, e.g., the Coulomb force formula above, changes, so the electromagnetic force strength gets altered under the influence of a passing gravitational wave, which if strong enough can then tear a person apart. One could thus measure gravitational waves, ideally with instruments that are sensitive to distance differential variations across two orthogonally oriented arms, in view of the form of the tidal tensor. Michelson interferometers constitute obvious candidates. Gravitational wave strain h is defined by the stretch and squash length difference in Michelson interferometer arms as:

\(\begin{aligned} h=\frac{2\Delta L}{L}, \end{aligned}\)
(1)

where \(\Delta L\) is the change in arm length caused by a passing gravitational wave signal, and L is the original Michelson arm length. Unfortunately for gravitational scientists, and fortunately for everybody else, there are no colliding black holes in our vicinity, so any signal would have traversed great expanse on its way here and weaken significantly in the process, to such a level that the distance differentials it engender would be far smaller than the wavelength of the lasers we possess, leading to minuscule phase differences for us to gauge, so much so that the quantum nature of light could become the limiting factor for sensitivity. The paramount task for an experimenter is thus to suppress noises, at least to a level that some detections can plausibly be made during the span of a typical scientist’s career.

1.2 Noises

Gravitational wave amplitude declines as the inverse of distance to source, so dropping the noise level by a factor of ten would increase detection distance by an order of magnitude. Since we live in three spatial dimensions, this then translates into an increase in the potential source volume and subsequently the potential event rate by a factor of a thousand (without accounting for local density variations of galaxies). Investments in the reduction of noises is well worth the trouble and is indeed the main thrust of experimental efforts.

Noises creep in at each stage of the measurement process, and have been analytically modeled, see Fig. 1. They can be roughly grouped into four major types according to which component of the detector system that they contaminate:

  • Displacement noises that enter into the mechanical components. These are excitation of the mechanical components of an interferometer that engenders uncertainty in the distance between the mirrors, and can be sub-divided into the following types:

    1. Seismic noise: to mitigate this problem, one would place the mirrors on moving platforms controlled by feedback systems [17, 18]. The control reacts quickly enough to neutralize the large amplitude, low frequency motions of the ground. Then, to handle the higher frequencies, one can hang the mirrors within multi-stage damped harmonic oscillators, which act as passive isolation [19, 20] that filters out motions above the resonant frequency. One can understand the working principle by playing with a pendulum, if one shakes the hand holding onto the top of the pendulum fast enough, the pendulum does not in fact react much. The advantage of multi-staging is that it causes even steeper decline of the pendulum response as a function of increasing frequency [21].

    2. Thermal motion occurs within the mirror substrate, its optical coating material, and the suspension wires or glass fibers. One can select the substrate and suspension materials according to mechanical or thermal qualities, but coatings must excel in their optical properties and thus are usually the most difficult to optimize [22,23,24,25,26,27,28,29,30,31,32]. We have a plethora of such thermal noises:

      • Brownian motion: this excites the mirror body modes and the pendulum modes in the suspension fibers.

      • Thermo-elastic noise: temperature fluctuations causes mirror motion and displacement [31].

      • Thermo-refractive noise: this is another ill effect due to temperature fluctuations, which causes variability in the mirror refractive index. Fortunately, this can be carefully tuned to largely cancel against its thermo-elastic brethren [33, 34].

    3. Newtonian gravity noise or gravity gradient noise: changes in the gravitational field around the test masses (i.e., the mirrors) that are not related to gravitational waves from distant sources fall in this category. They could be due to seismic surface wave (affecting test masses via gravity rather than electromagnetic forces transmitted by the suspension as in the case of seismic noise), moving clouds, or potentially even water flow in the tunnel housing the detector arms. To mitigate the effect of this type of noises, we could go underground, shape local topography, or use feedforward subtraction [35, 36].

  • Optical noises that affect the optics. The interferometer measures phase difference between two beams of light; thus, any noise entering into the optics feed through to the final readout. They could take the following forms:

    • Shot noise: due to the intrinsic uncertainty associated with quantum mechanics, the number of photons arriving at any mirror over any specified period of time cannot be completely fixed. One can statistically depict this situation with a Poisson distribution, thus the name. This translates into a fluctuation in the output power (number of photons being counted by the photodetector), whose inverse ratio against the signal (i.e., the signal to noise ratio) goes as one over the square root of the output power, as per usual with Poisson statistics. Thus, the simplest remedy is to turn up the laser power. Equivalently, because the photodetector measures the phase differential, the uncertainty in the number of photons it receives can be transcribed into the phase uncertainty of an electric field.

    • Radiation pressure noise: because the laser exerts force on the mirrors, the photon number fluctuation also creates a jitter in the mirror motion, and this effect (can be ascribed to the amplitude uncertainty of the electric field that fuzzes up its momentum) unfortunately goes up as the square root of the laser power (see e.g., [37,38,39,40] for subtleties). There is thus a see-sawing between the shot and the radiation pressure noises, reflecting the irreducibility of Heisenberg uncertainty between a pair of noncommuting observables, preventing them from being simultaneously suppressed, leading to this so-called Standard Quantum Limit [41]. The quantum noise of a simple Michelson can be modeled as

      \(\begin{aligned} h_{\mathrm {qn}}(\Omega )=\sqrt{h_{\mathrm {sh}}^{2}(\Omega )+h_{\mathrm {rp}}^{2}(\Omega )}=\frac{1}{L} \sqrt{\frac{\hbar c^2}{I\omega _0}+\frac{2I\hbar \omega _0}{m^2\Omega ^4c^2}}\ge \underbrace{\frac{1}{L}\sqrt{\frac{8\hbar }{m\Omega ^2}}}_{\text {SQL}}, \end{aligned}\)
      (2)

      where I is the incident power, L arm length, m mirror mass, \(w_0\) the laser frequency, and \(\Omega\) the frequency of gravitational wave signal. A plot showing the quantum noise of a toy LIGO model can be seen in Fig. 2.

    • There are also optic noises that are less physics limited, yet more demanding of engineering finesse: laser frequency and intensity fluctuations can be subdued with pre-stabilized laser sources that contain a pre-mode cleaner together with frequency and power stabilization servos. Scattered light noise comes from stray laser light being reflected by, e.g., the vacuum tube walls, and picks up the trembles in these tubes (only the mirrors are insulated against displacement noises)—roomier tubes would help. Furthermore, the mirrors can absorb some of the laser light and end up exhibiting altered characteristics, which can be controlled with adaptive optical techniques [42,43,44].

  • Residual gas in the vacuum chamber and pipes causes excess phase shift compared with the same length path propagating in vacuum. It therefore becomes a noise source for gravitational wave detection and can be modeled by the dominant molecule component hydrogen with present achieved pressure level. This type of noise still sits well below other technical noises and is beyond the scope of this note. Interested reader may find further materials in [45, 46].

  • Electrical noises arising in the electronics. These do not represent the most significant problem in any frequency range, so we do not go into more details here.

Fig. 1
figure 1

Noise budget of Advanced LIGO showing its major noise sources. This plot was reproduced by pygwinc [https://git.ligo.org/gwinc/pygwinc] [16]


Fig. 2
figure 2

Quantum noise levels of a toy model, giving AdLIGO test mass (40kg) with 1000 W(blue), 100 kW(green), and 10 MW(red) incident powers respectively. The shot noise at high frequencies decreases with higher power; however, the radiation pressure noise increases. The black line shows quantum noise, a sum of minimum shot noise, and radiation pressure noise, over different laser powers, which forms a boundary of quantum noise called the Standard Quantum Limit (SQL)


All of these potential noise sources have been modeled theoretically in exquisite details and match actual measurements . One feature we learn from this effort is that seismic noise dominates the low frequencies, thermal noises the middle, and most sensitive range, while the quantum shot noise limits the sensitivity at the higher frequency ranges.

Considering the primitive state of technological know-how and in particular our sparse theoretical understanding of the vast plethora of noises at the beginning of the endeavor to search for gravitational waves, it is truly extraordinary that theory and experiment progressed hand-in-hand with such precision and cohesion, which eventually overcame the impossible to yield the first detection in 2015 [47], for which the 2017 Nobel physics prize was awarded. Nowadays, the global detector network of LIGO-Virgo-KAGRA routinely detect [48] binary black hole, neuron star binary, and mixed neutron star-black hole coalescence, yielding much insight and even more surprises. The next frontier in gravitational wave science is to up the accuracy of the detected waveform and look for finer details such as echos [49] that reflect potential modifications to General Relativity, and also to explore broader frequency ranges, in particular a higher one ranging from thousands to tens of thousands of Hertz, in which the more violent and thus matter-property-sensitive merger and ringdown (settling of the amalgam) stages of binary neutron star coalescence events lie [50,51,52], that could thus inform on such important physics as the equation of state of ultra-dense matter. To this end, the two quantum optic noises, shot and radiation reaction, are increasingly becoming the limiting factors for detector sensitivity, as the other more classical noises are either being aggressively and successfully reigned in or beyond the interesting frequency band. We have seen that tuning the laser power alone does not quite solve the problem for us, so one might look to new technique for a plausible way forward, the squeezing of the laser light.

This is the main topic of this note, yet our introduction to the present state of application of squeezing to the detection of gravitational waves is extremely brief however, and interested readers should consult, e.g., [53,54,55].

2 Quantum noise

2.1 Vacuum fluctuation

Within the interferometer context, it is at the asymmetric port that vacuum fluctuation couples to the differential quantum noises in the two arms as illustrated by Fig. 3. Unlike the normal expression of quantized electronic field based on linear superposition of the annihilation operator and creation operator, two-photon formalism was introduced by Caves and Schumaker [38] which has been used ever since within the gravitational wave community, and the electric field is written in terms of quadrature operators \(\hat{a}_1\) and \(\hat{a}_2\) as

\(\begin{aligned} \hat{E}(t) = \cos (\omega _0t)\hat{a}_1(t)+\sin (\omega _0t)\hat{a}_2(t). \end{aligned}\)
(3)

The quadrature operators definition could be found in [38] and usually in frequency domain. They are two classical meaning of quadratures, representing the magnitude of the amplitude and phase vacuum fluctuations, one in phase with the laser light, one out of phase. The former is associated with anti-correlated power fluctuations between the two arms, or in other words the radiation reaction noise, while the latter couples to the phase differential, or shot noise. It is at this vacuum port one should enforce the squeezed state [56, 57]. One can squeeze either to suppress the corresponding quantum noise. This may seem counter to our classical intuition, that preciously few photons injected from a largely vacuum port would be able to herd the huge number of carrier photons so effectively, but a quantum field is distributed and so does not need local manifestations in the form of an army of photons visiting the vacuum port to know that there are apparatus waiting there to squeeze it. In other words, photons are just the visible tip of the iceberg, and there are much more intrigue going on underneath that we do not see, which is really what is being constrained by the squeezing equipment.

Fig. 3
figure 3

Vacuum fluctuations enter the main interferometer through the asymmetric port or so-called dark port within the community. Anti-correlated power and phase fluctuations exist in the two arms and associate with the quantum noise of gravitational wave detectors


2.2 Squeezing

In the present incarnation of gravitational wave detector applications [53, 55, 58,59,60,61], a sub-threshold optical parametric oscillator (in a bow-tie cavity configuration) uses three-wave mixing in temperature-controlled periodically poled potassium titanyl phosphate crystal to down-convert frequency doubled (as compared to carrier; produced using a second harmonic generator containing the same type of nonlinear crystal) photons into a pair of non-degenerate entangled photons, with symmetric sideband frequencies shifted from the central carrier frequency by the audio band observation frequency (see, e.g., [62]). This system has a Hamiltonian that gives rise to the unitary evolution of a reflected vacuum in the form of a squeezing operator as below:

\(\begin{aligned} {\hat{\mathbf {a}}_s}(\Omega )= & {} {\mathbf {R}}[-\phi ] \left[ \begin{array}{cc} e^{r} &{} 0\\ 0 &{} e^{-r} \end{array}\right] {\mathbf {R}}[\phi ]{\hat{\mathbf {a}}}(\Omega )\nonumber \\= & {} \left[ \begin{array}{cc} \cosh r +\sinh r\cos 2\phi &{} -\sinh r \sin 2\phi \\ -\sinh r \sin 2\phi &{} \cosh r -\sinh r\cos 2\phi \end{array}\right] {\hat{\mathbf {a}}}(\Omega ), \end{aligned}\)
(4)

where

\(\begin{aligned} \mathbf {R}[\phi ] = \left[ \begin{array}{cc} \cos \phi &{} -\sin \phi \\ \sin \phi &{} \cos \phi \end{array}\right] , \end{aligned}\)

is the rotation matrix with \(\phi\) being the squeezing angle, and r is the squeezing factor. This could potentially reduce the quantum noise by a factor of \(e^{-2r}\) with desired rotation angle. Squeezing process can be visualized as the vacuum fluctuation with an equal uncertainty at both phase and amplitude quadratures, round shape fuzzy ball as shown by the left image in Fig. 4(a), enters a nonlinear optical system (see also an alternative ponderomotive squeezing technique [63, 64], which converts amplitude fluctuations into phase jitters through reflecting off mirrors) which creates correlation between the phase and amplitude quadrature and then squeezes the uncertainty ball into an elliptical shape with a squeezing angle. One would refer to a phase squeezed vacuum and amplitude squeezed vacuum as illustrated by Fig. 4(a) and (b) respectively, which accordingly has the smallest phase uncertainty or amplitude uncertainty. Squeezing degree is often scaled in dB, i.e., a 10 dB phase squeezing corresponding to \(r=0.5\ln 10\) and \(\phi = 0\). It can be understood by the ratio of two quadratures, the narrower of the elliptical fuzzy ball the better of the squeezing as compared in Fig. 4(c) and (d).

Fig. 4
figure 4

Squeezing application in gravitational wave detectors. External nonlinear optics create correlation between the phase and amplitude quadrature which turns the vacuum fluctuation into a squeezed state. Squeezing in a desired angle then enters into the main interferometer which could potentially reduce the the quantum noise. (a–c) Squeezing with different squeezing angles and the elliptical squashed level illustrated in (c) and (d) visualizes the squeezing degree, here with 10 dB and 15 dB respectively


Indeed, it should not surprise that nonlinear interactions tend to distort the round shape, away from the coherent state of light coming straight out of a stabilized laser source. One just needs to contrive setups that distort it into the shapes we desire, and which are possible to physically realize given available technology. Immediately though, one may ask that since interferometers measure phase, couldn’t one just squeeze the phase of laser light to the limit of decoherence and be done with it? Why would one care about the expanse of an increased amplitude uncertainty? Indeed, this strategy pushes down optical noise, but the issue is that the amplitude fluctuations leak into displacement noise and re-enter under a different disguise, becoming a part of the signal for the optical system. Since it is the total noise that we care about, this approach is not quite optimal.

3 Squeezing enhancing gravitational wave detection

Similar to the laser power tuning (see Fig. 2), squeezing injection with a unique angle will not help reduce the total noise over a broad frequency band. There is always a trade-off between the shot noise and radiation pressure noise. How to employ the squeezing technology for an overall quantum noise reduction becomes a key problem.

Luckily, we have a fortunate feature though that the mirror hung by a multi-stage mechanical pendulum reacts more to the lower frequency radiation pressure noise, so the two types of quantum optic noises have different frequency profiles. In other words, we could plausibly exploit the fact that the uncertainty in the final readout is not simply a function of the quadrature sum of uncertainties in a pair of conjugate observables, but instead contains various transfer functions assigning different and variable weights to each observable, and use frequency-dependent squeezing to concentrate on curbing respectively the more dominant source of noise in each frequency interval, in order to achieve an overall broadband improvement. In short, gravitational wave detection desires amplitude squeezing at low frequencies and phase squeezing at high frequencies. It is known that quadrature rotation angle and additional phase shift reflected by a detuned cavity both show a frequency-dependent feature. Filter cavities then have been investigated and successfully demonstrated, which indeed give desired frequency-dependent quadrature rotation by carefully choosing its linewidth and detuning. The necessary theoretical and technical specifications for achieving frequency dependence, by reflecting the laser off a filter cavity detuned from the main carrier frequency, can be found in [65,66,67,68,69].

Filter cavities are placed after the squeezer and before the main interferometer as shown by the left picture of Fig. 5. A phase squeezed state will be filtered by the cavity, and when it enters the interferometer, the squeezing state rotates to its desired angle at each frequencies, illustrated in the bottom of the diagram, for gravitational wave detection. The overall quantum noise of Advanced LIGO will be reduced and eventually surpasses the SQL as shown in the right plot of Fig. 5. As expected, better squeezing level would further enhance the performance of a gravitational wave detector. However, in reality squeezing level degrades in various ways, e.g., losses, phase noise, control noise, etc., and of which the most common issue is due to optical losses in the whole system, including the squeezer itself, the main interferometer and also the filter cavities, where unsqueezed vacuum state leaks in and dilutes the squeezing through the lossy port. Lots of ideas have been proposed and demonstrated to achieve higher level of squeezing [70,71,72,73,74]. Meanwhile, due to the extremely sensitive nature of gravitational wave detectors, extra care must be taken to ensure that these extra squeezer and filter cavities do not induce new noise that will cover up gravitational wave signals.

Fig. 5
figure 5

Frequency-dependent squeezing enhancing Advanced LIGO in an ideal model. Filter cavities are applied to rotate the angle of squeezed state. A phase squeezing will be manipulated to the desired squeezing angle at different frequencies. The quantum vacuum noise was extracted from the noise budget of Advanced LIGO as shown in Fig. 1, recalculated with pygwinc [16]. By applying the frequency-dependent squeezing, quantum noise is reduced over a broad frequency band and the SQL can be surpassed in this way


It is important to note that squeezing technology as it stands, without employing any of the strategies in these references, already has a frequency dependence. To our detriment, squeezing is more readily achievable in the megahertz regime (see, e.g., [75]), but for gravitational wave detection, the target range is audio band.

4 Summary and outlook

Squeezing has become one of the most reliable techniques for gravitational wave detection to reach more potential astrophysical events. After many years of investigation, a whole host of innovative designs combine to yield 10 dB down to as low as 10 Hz and squeezed state injection is now included in all the designs of future generation detectors.

The implementation of squeezing is promising but squeezing degradation due to optical losses, mode matching efficiency, etc., is a major issue preventing the best performance of gravitational wave detectors, particularly with auxiliary filter cavities realizing broadband quantum noise reduction. Fortunately, the specific class of future kilo-Hertz gravitational-wave detector for neutron-star physics will be an exception with no need of filter cavities, as at its target frequency-band (2–4 kHz) shot noise will be the only limiting noise sources. As such, these detectors represent ideal race tracks for competing squeezing strategies that focus entirely on ramping up the decibels. In particular, they offer up exquisite vacuum environments and obsessive suppression of a whole cohort of other classical complications such as thermal and seismic fluctuations, which would enter into the quantum computation as sources of decoherence. Such advantages are not afforded by desktop experiments through which the science of squeezing had traditionally been pursued.

In other words, we join other, more prominent, gravitational wave researchers in advertising high-frequency gravitational wave detectors as not only avenues for the application of squeezing, but also the stages on which the future develop of squeezing techniques themselves could play out. It is an opportune time to extend an invitation to the pure quantum optics community, and solicit brainstorms on such fundamental issues as exotic cavity designs and concoctions of nonlinearity, which could be realized at the various prototypes for the next generation gravitational wave detectors, including our own.

Availability of data and materials

N/A

Code availability

N/A

Notes

  1. But do not have to be, there can be entire curved universes without matter, admitting only Weyl curvature while the Ricci curvature vanishes everywhere.

  2. The Einstein’s equations together with the Bianchi identities can be written in a form resembling the Maxwell’s equations, thus the proliferation of analogies.

References

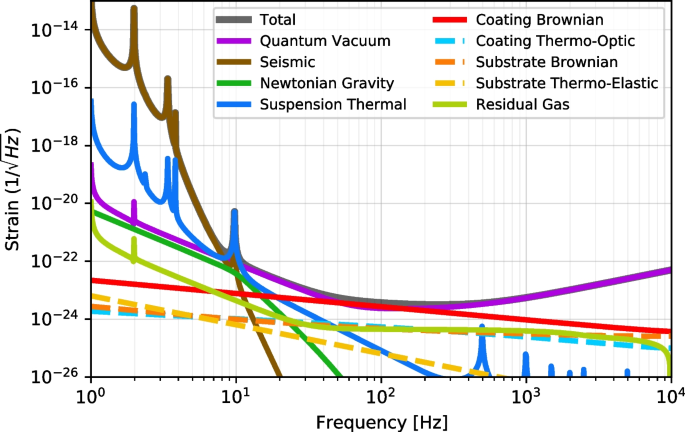
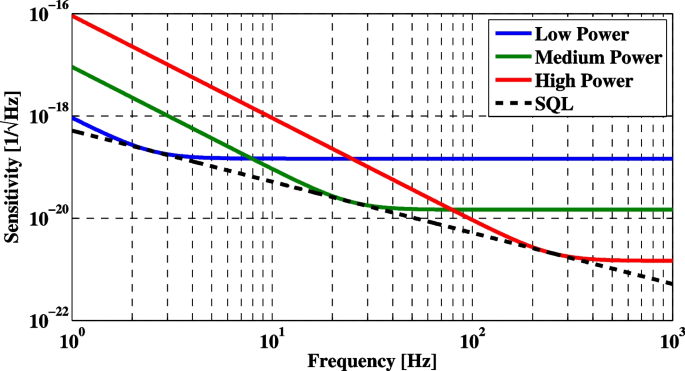
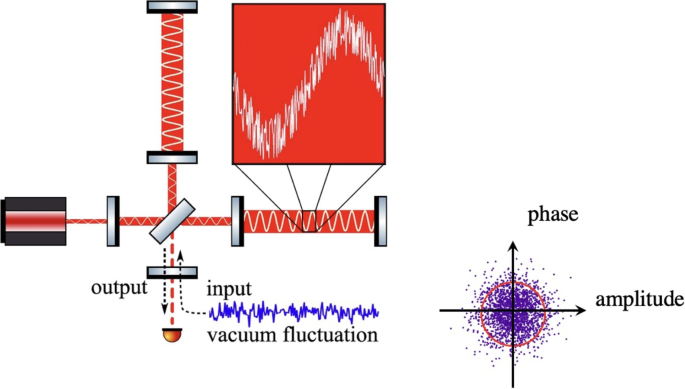
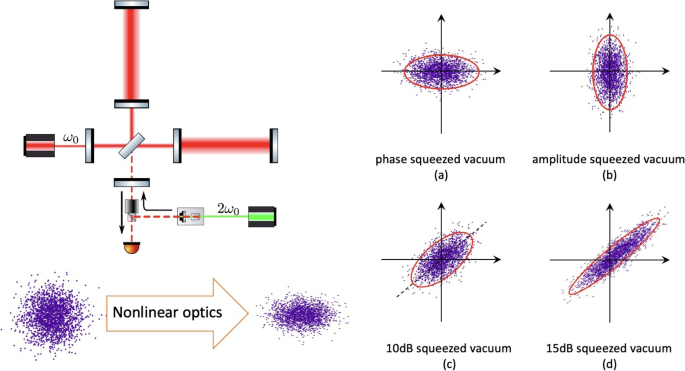
  1. X.Y. Lü, Y. Wu, J. Johansson, H. Jing, J. Zhang, F. Nori, Squeezed optomechanics with phase-matched amplification and dissipation. Phys. Rev. Lett. 114(9), 093602 (2015)

  2. M. Asjad, S. Zippilli, D. Vitali, Suppression of stokes scattering and improved optomechanical cooling with squeezed light. Phys. Rev. A 94(5), 051801 (2016)

  3. J.B. Clark, F. Lecocq, R.W. Simmonds, J. Aumentado, J.D. Teufel, Sideband cooling beyond the quantum backaction limit with squeezed light. Nature 541(7636), 191–195 (2017)

  4. N. Didier, A. Kamal, W.D. Oliver, A. Blais, A.A. Clerk, Heisenberg-limited qubit read-out with two-mode squeezed light. Phys. Rev. Lett. 115(9), 093604 (2015)

  5. W. Qin, A. Miranowicz, P.B. Li, X.Y. Lü, J.Q. You, F. Nori, Exponentially enhanced light-matter interaction, cooperativities, and steady-state entanglement using parametric amplification. Phys. Rev. Lett. 120(9), 093601 (2018)

  6. Y.H. Chen, W. Qin, X. Wang, A. Miranowicz, F. Nori, Shortcuts to adiabaticity for the quantum rabi model: Efficient generation of giant entangled cat states via parametric amplification. Phys. Rev. Lett. 126(2), 023602 (2021)

  7. W. Qin, V. Macrì, A. Miranowicz, S. Savasta, F. Nori, Emission of photon pairs by mechanical stimulation of the squeezed vacuum. Phys. Rev. A 100(6), 062501 (2019)

  8. M. Asjad, N.E. Abari, S. Zippilli, D. Vitali, Optomechanical cooling with intracavity squeezed light. Opt. Express 27(22), 32427–32444 (2019)

  9. W. Qin, A. Miranowicz, H. Jing, F. Nori, Generating long-lived macroscopically distinct superposition states in atomic ensembles. Phys. Rev. Lett. 127(9), 093602 (2021)

  10. H.S. Zhong, H. Wang, Y.H. Deng, M.C. Chen, L.C. Peng, Y.H. Luo, J. Qin, D. Wu, X. Ding, Y. Hu et al., Quantum computational advantage using photons. Science 370(6523), 1460–1463 (2020)

  11. H.S. Zhong, Y.H. Deng, J. Qin, H. Wang, M.C. Chen, L.C. Peng, Y.H. Luo, D. Wu, S.Q. Gong, H. Su et al., Phase-programmable gaussian boson sampling using stimulated squeezed light. Phys. Rev. Lett. 127(18), 180502 (2021)

  12. W. Qin, A. Miranowicz, F. Nori, Beating the 3 db limit for intracavity squeezing and its application to nondemolition qubit readout. (2022). arXiv preprint arXiv:2203.06892

  13. S.C. Burd, R. Srinivas, H.M. Knaack, W. Ge, A.C. Wilson, D.J. Wineland, D. Leibfried, J.J. Bollinger, D. Allcock, D. Slichter, Quantum amplification of boson-mediated interactions. Nat. Phys. 17(8), 898–902 (2021)

  14. W. Qin, Y.H. Chen, X. Wang, A. Miranowicz, F. Nori, Strong spin squeezing induced by weak squeezing of light inside a cavity. Nanophotonics 9(16), 4853–4868 (2020)

  15. R. Owen, J. Brink, Y. Chen, J.D. Kaplan, G. Lovelace, K.D. Matthews, D.A. Nichols, M.A. Scheel, F. Zhang, A. Zimmerman, K.S. Thorne, Frame-dragging vortexes and tidal tendexes attached to colliding black holes: visualizing the curvature of spacetime. Phys. Rev. Lett. 106(15), 151101 (2011). https://doi.org/10.1103/PhysRevLett.106.151101

  16. GWINC: Gravitational Wave Interferometer Noise Calculator. http://lhocds.ligo-wa.caltech.edu:8000/advligo/GWINC. V1 default parameters

  17. J.M. Hensley, A. Peters, S. Chu, Active low frequency vertical vibration isolation. Rev. Sci. Instrum. 70(6), 2735 (1999)

  18. D.B. Newell, S.J. Richman, P.G. Nelson, R.T. Stebbins, P.L. Bender, J.E. Faller, J. Mason, An ultra-low-noise, low-frequency, six degrees of freedom active vibration isolator. Rev. Sci. Instrum. 68(8), 3211 (1997)

  19. F. Matichard, et al., Advanced LIGO two-stage twelve-axis vibration isolation and positioning platform. Part 1: Design and production overview. (2014). arXiv:1407.6377

  20. F. Matichard, et al., Advanced LIGO two-stage twelve-axis vibration isolation and positioning platform. Part 2: Experimental investigation and tests results. (2014). arXiv:1407.6324

  21. S.M. Aston et al., Update on quadruple suspension design for Advanced LIGO. Class. Quant. Grav. 29(23), 235004 (2012). https://doi.org/10.1088/0264-9381/29/23/235004

  22. R. Bassiri, K. Evans, K. Borisenko, M. Fejer, J. Hough, I. MacLaren, I. Martin, R. Route, S. Rowan, Correlations between the mechanical loss and atomic structure of amorphous TiO2-doped Ta2O5 coatings. Acta Mater. 61(4), 1070–1077 (2013)

  23. K. Evans, R. Bassiri, I. Maclaren, S. Rowan, I. Martin, J. Hough, K. Borisenko, Reduced density function analysis of titanium dioxide doped tantalum pentoxide. J. Phys. Conf. Ser. 371, 012058 (2012)

  24. T. Hong, H. Yang, E.K. Gustafson, R.X. Adhikari, Y. Chen, Brownian thermal noise in multilayer coated mirrors. Phys. Rev. D87(8), 082001 (2013)

  25. R. Flaminio, J. Franc, C. Michel, N. Morgado, L. Pinard et al., A study of coating mechanical and optical losses in view of reducing mirror thermal noise in gravitational wave detectors. Class. Quant. Grav. 27, 084030 (2010). https://doi.org/10.1088/0264-9381/27/8/084030

  26. N. Kondratiev, A. Gurkovsky, M. Gorodetsky, Thermal noise and coating optimization in multilayer dielectric mirrors. Phys. Rev. D 84, 022001 (2011). https://doi.org/10.1103/PhysRevD.84.022001

  27. G.M. Harry, M.R. Abernathy, A.E. Becerra-Toledo, H. Armandula, E. Black et al., Titania-doped tantala/silica coatings for gravitational-wave detection. Class. Quant. Grav. 24, 405–416 (2007). https://doi.org/10.1088/0264-9381/24/2/008

  28. G.M. Harry, H. Armandula, E. Black, D.R.M. Crooks, G. Cagnoli, J. Hough, P. Murray, S. Reid, S. Rowan, P. Sneddon, M.M. Fejer, R. Route, S.D. Penn, Thermal noise from optical coatings in gravitational wave detectors. Appl. Opt. 45(7), 1569 (2006)

  29. G.M. Harry, A.M. Gretarsson, P.R. Saulson, S.E. Kittelberger, S.D. Penn et al., Thermal noise in interferometric gravitational wave detectors due to dielectric optical coatings. Class. Quant. Grav. 19, 897–918 (2002). https://doi.org/10.1088/0264-9381/19/5/305

  30. S. Rowan, J. Hough, D. Crooks, Thermal noise and material issues for gravitational wave detectors. Phys. Lett. A 347, 25–32 (2005). https://doi.org/10.1016/j.physleta.2005.06.055

  31. V.B. Braginsky, S.P. Vyatchanin, Thermodynamical fluctuations in optical mirror coatings. Phys. Lett. A 312, 244–255 (2003). https://doi.org/10.1016/S0375-9601(03)00473-0

  32. S.D. Penn, P.H. Sneddon, H. Armandula, J.C. Betzwieser, G. Cagnoli et al., Mechanical loss in tantala / silica dielectric mirror coatings. Class. Quant. Grav. 20, 2917–2928 (2003). https://doi.org/10.1088/0264-9381/20/13/334

  33. M. Evans, S. Ballmer, M. Fejer, P. Fritschel, G. Harry et al., Thermo-optic noise in coated mirrors for high-precision optical measurements. Phys. Rev. D 78, 102003 (2008). https://doi.org/10.1103/PhysRevD.78.102003

  34. G. Harry, T. Bodiya, R. DeSalvo, Optical Coatings and Thermal Noise in Precision Measurement. Cambridge: Cambridge University Press. (2012). https://doi.org/10.1017/CBO9780511762314, https://www.cambridge.org/core/books/optical-coatings-and-thermal-noise-in-precisionmeasurement/705BC46F0FC70827BF8C986F07489A1B

  35. J.C. Driggers, J. Harms, R.X. Adhikari, Subtraction of Newtonian noise using optimized sensor arrays. Phys. Rev. D 86, 102001 (2012). https://doi.org/10.1103/PhysRevD.86.102001

  36. J. Harms, S. Hild, Passive Newtonian noise suppression for gravitational-wave observatories based on shaping of the local topography. Class. Quant. Grav. 31, 185011 (2014). https://doi.org/10.1088/0264-9381/31/18/185011

  37. C. Caves, Quantum mechanical noise in an interferometer. Phys. Rev. D 23, 1693–1708 (1981). https://doi.org/10.1103/PhysRevD.23.1693

  38. C.M. Caves, B.L. Schumaker, New formalism for two-photon quantum optics. 1. Quadrature phases and squeezed states. Phys. Rev. A31, 3068–3092 (1985). https://doi.org/10.1103/PhysRevA.31.3068

  39. B.L. Schumaker, C.M. Caves, New formalism for two-photon quantum optics. 2. Mathematical foundation and compact notation. Phys. Rev. A31, 3093–3111 (1985). https://doi.org/10.1103/PhysRevA.31.3093

  40. R. Loudon, Quantum limit on the Michelson interferometer used for gravitational wave detection. Phys. Rev. Lett. 47, 815–818 (1981). https://doi.org/10.1103/PhysRevLett.47.815

  41. V.B. Braginsky, F.Y. Khalili, Quantum Measurement (Cambridge University Press, 1999)

  42. P. Hello, J. Vinet, Numerical model of transient thermal effects in high power optical resonators. J. Phys. (France) 51, 1267 (1990)

  43. W. Winkler, K. Danzmann, A. Rüdiger, R. Schilling, Heating by optical absorption and the performance of interferometric gravitational wave detectors. Phys. Rev. A 44, 7022–7036 (1991). https://doi.org/10.1103/PhysRevA.44.7022

  44. R. Lawrence, D. Ottaway, M. Zucker, P. Fritschel, Active correction of thermal lensing through external radiative thermal actuation. Opt. Lett. 29, 2635 (2004)

  45. P.R. Saulson, Fundamentals of Interferometric Gravitational Wave Detectors, 2nd edn. (World Scientific, 2017). https://doi.org/10.1142/10116

  46. J. Aasi, B.P. Abbott, R. Abbott, T. Abbott, M.R. Abernathy, K. Ackley et al., Advanced ligo. Class. Quantum Gravity 32, 074001 (2015). https://doi.org/10.1088/0264-9381/32/7/074001

  47. B.P. Abbott, R. Abbott, T.D. Abbott, M.R. Abernathy, F. Acernese, K. Ackley et al., Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116(6), 061102 (2016). https://doi.org/10.1103/PhysRevLett.116.061102

  48. The LIGO Scientific Collaboration, et al., GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo During the Second Part of the Third Observing Run. (2021). arXiv e-prints arXiv:2111.03606

  49. R.A. Konoplya, Z. Stuchlík, A. Zhidenko, Echoes of compact objects: new physics near the surface and matter at a distance. Phys. Rev. D 99(2), 024007 (2019). https://doi.org/10.1103/PhysRevD.99.024007

  50. A.L. Piro, B. Giacomazzo, R. Perna, The fate of neutron star binary mergers. Astrophys. J. Lett. 844(2), L19 (2017). https://doi.org/10.3847/2041-8213/aa7f2f

  51. H. Miao, H. Yang, D. Martynov, Towards the design of gravitational-wave detectors for probing neutron-star physics. Phys. Rev. D 98, 044044 (2018). https://doi.org/10.1103/PhysRevD.98.044044

  52. D. Martynov, H. Miao, H. Yang, F.H. Vivanco, E. Thrane, R. Smith, P. Lasky, W.E. East, R. Adhikari, A. Bauswein, A. Brooks, Y. Chen, T. Corbitt, A. Freise, H. Grote, Y. Levin, C. Zhao, A. Vecchio, Exploring the sensitivity of gravitational wave detectors to neutron star physics. Phys. Rev. D 99, 102004 (2019). https://doi.org/10.1103/PhysRevD.99.102004

  53. Ligo Scientific Collaboration, J. Abadie, B.P. Abbott, R. Abbott, T.D. Abbott, M. Abernathy, C. Adams et al., A gravitational wave observatory operating beyond the quantum shot-noise limit. Nat. Phys. 7(12), 962–965 (2011). https://doi.org/10.1038/nphys2083

  54. S.E. Dwyer, G.L. Mansell, L. McCuller, Squeezing in gravitational wave detectors. Galaxies 10(2), 46 (2022). https://doi.org/10.3390/galaxies10020046

  55. S. Chua, M. Stefszky, C. Mmow-Lowry, B.C. Buchler, K. McKenzie, D.A. Shaddock, P.K. Lam, D.E. McClelland, Quantum squeezing in advanced gravitational wave detectors. Int. J. Mod. Phys. D 20(10), 2043–2049 (2011). https://doi.org/10.1142/S0218271811020159

  56. C.M. Caves, B.L. Schumaker, New formalism for two-photon quantum optics. I. Quadrature phases and squeezed states. Phys. Rev. A 31(5), 3068–3092 (1985). https://doi.org/10.1103/PhysRevA.31.3068

  57. B.L. Schumaker, C.M. Caves, New formalism for two-photon quantum optics. II. Mathematical foundation and compact notation. Phys. Rev. A 31(5), 3093–3111 (1985). https://doi.org/10.1103/PhysRevA.31.3093

  58. H. Grote, K. Danzmann, K.L. Dooley, R. Schnabel, J. Slutsky, H. Vahlbruch, First long-term application of squeezed states of light in a gravitational-wave observatory. Phys. Rev. Lett. 110(18), 181101 (2013). https://doi.org/10.1103/PhysRevLett.110.181101

  59. K. McKenzie, M.B. Gray, S. Goßler, P.K. Lam, D.E. McClelland, Squeezed state generation for interferometric gravitational-wave detection. Class. Quantum Gravity 23(8), S245–S250 (2006). https://doi.org/10.1088/0264-9381/23/8/S31

  60. J. Aasi, J. Abadie, B.P. Abbott, R. Abbott, T.D. Abbott, M.R. Abernathy et al., Enhanced sensitivity of the LIGO gravitational wave detector by using squeezed states of light. Nat. Photonics 7(8), 613–619 (2013). https://doi.org/10.1038/nphoton.2013.177

  61. M.S. Stefszky, C.M. Mow-Lowry, S.S.Y. Chua, D.A. Shaddock, B.C. Buchler, H. Vahlbruch, A. Khalaidovski, R. Schnabel, P.K. Lam, D.E. McClelland, Balanced homodyne detection of optical quantum states at audio-band frequencies and below. Class. Quantum Gravity 29(14), 145015 (2012). https://doi.org/10.1088/0264-9381/29/14/145015

  62. L. Barsotti, J. Harms, R. Schnabel, Squeezed vacuum states of light for gravitational wave detectors. Rep. Prog. Phys. 82(1), 016905 (2019). https://doi.org/10.1088/1361-6633/aab906

  63. H.J. Kimble, Y. Levin, A.B. Matsko, K.S. Thorne, S.P. Vyatchanin, Conversion of conventional gravitational-wave interferometers into quantum nondemolition interferometers by modifying their input and/or output optics. Phys. Rev. D 65(2), 022002 (2001)

  64. S.L. Danilishin, F.Y. Khalili, H. Miao, Advanced quantum techniques for future gravitational-wave detectors. Living Rev. Relativ. 22(1), 2 (2019). https://doi.org/10.1007/s41114-019-0018-y

  65. H.J. Kimble, Y. Levin, A.B. Matsko, K.S. Thorne, S.P. Vyatchanin, Conversion of conventional gravitational-wave interferometers into quantum nondemolition interferometers by modifying their input and/or output optics. Phys. Rev. D 65(2), 022002 (2001). https://doi.org/10.1103/PhysRevD.65.022002

  66. S. Chelkowski, H. Vahlbruch, B. Hage, A. Franzen, N. Lastzka, K. Danzmann, R. Schnabel, Experimental characterization of frequency-dependent squeezed light. Phys. Rev. A 71(1), 013806 (2005). https://doi.org/10.1103/PhysRevA.71.013806

  67. E. Oelker, T. Isogai, J. Miller, M. Tse, L. Barsotti, N. Mavalvala, M. Evans, Audio-band frequency-dependent squeezing for gravitational-wave detectors. Phys. Rev. Lett. 116(4), 041102 (2016). https://doi.org/10.1103/PhysRevLett.116.041102

  68. ...Y. Zhao, N. Aritomi, E. Capocasa, M. Leonardi, M. Eisenmann, Y. Guo, E. Polini, A. Tomura, K. Arai, Y. Aso, Y.C. Huang, R.K. Lee, H. Lück, O. Miyakawa, P. Prat, A. Shoda, M. Tacca, R. Takahashi, H. Vahlbruch, M. Vardaro, C.M. Wu, M. Barsuglia, R. Flaminio, Frequency-dependent squeezed vacuum source for broadband quantum noise reduction in advanced gravitational-wave detectors. Phys. Rev. Lett. 124(17), 171101 (2020). https://doi.org/10.1103/PhysRevLett.124.171101

  69. L. McCuller, C. Whittle, D. Ganapathy, K. Komori, M. Tse, A. Fernandez-Galiana, L. Barsotti, P. Fritschel, M. MacInnis, F. Matichard, K. Mason, N. Mavalvala, R. Mittleman, H. Yu, M.E. Zucker, M. Evans, Frequency-dependent squeezing for advanced LIGO. Phys. Rev. Lett. 124(17), 171102 (2020). https://doi.org/10.1103/PhysRevLett.124.171102

  70. E. Genin, M. Mantovani, G. Pillant, C.D. Rossi, L. Pinard, C. Michel, M. Gosselin, J. Casanueva, Vacuum-compatible low-loss faraday isolator for efficient squeezed-light injection in laser-interferometer-based gravitational-wave detectors. Appl. Opt. 57(32), 9705–9713 (2018). https://doi.org/10.1364/AO.57.009705

  71. ...S.S.Y. Chua, S. Dwyer, L. Barsotti, D. Sigg, R.M.S. Schofield, V.V. Frolov, K. Kawabe, M. Evans, G.D. Meadors, M. Factourovich, R. Gustafson, N. Smith-Lefebvre, C. Vorvick, M. Landry, A. Khalaidovski, M.S. Stefszky, C.M. Mow-Lowry, B.C. Buchler, D.A. Shaddock, P.K. Lam, R. Schnabel, N. Mavalvala, D.E. McClelland, Impact of backscattered light in a squeezing-enhanced interferometric gravitational-wave detector. Class. Quantum Gravity 31(3), 035017 (2014). https://doi.org/10.1088/0264-9381/31/3/035017

  72. T. Isogai, J. Miller, P. Kwee, L. Barsotti, M. Evans, Loss in long-storage-time optical cavities. Opt. Express 21(24), 30114–30125 (2013). https://doi.org/10.1364/OE.21.030114

  73. H.T. Cao, A. Brooks, S.W.S. Ng, D. Ottaway, A. Perreca, J.W. Richardson, A. Chaderjian, P.J. Veitch, High dynamic range thermally actuated bimorph mirror for gravitational wave detectors. Appl. Opt. 59(9), 2784–2790 (2020). https://doi.org/10.1364/AO.376764

  74. V. Srivastava, G. Mansell, C. Makarem, M. Noh, R. Abbott, S. Ballmer, G. Billingsley, A. Brooks, H.T. Cao, P. Fritschel, D. Griffith, W. Jia, M. Kasprzack, M. MacInnis, S. Ng, L. Sanchez, C. Torrie, P. Veitch, F. Matichard, Piezo-deformable mirrors for active mode matching in advanced ligo. Opt. Express 30(7), 10491–10501 (2022). https://doi.org/10.1364/OE.445088

  75. T.C. Ralph, M.S. Taubman, A.G. White, D.E. McClelland, H.A. Bachor, Squeezed light from second-harmonic generation: experiment versus theory. Opt. Lett. 20(11), 1316–1318 (1995). https://doi.org/10.1364/OL.20.001316

Acknowledgements

The authors jointly thank Mengdi Cao for helping extract the quantum noise data from pygwinc. The authors acknowledge the ComponentLibrary by Alexander Franzen and Advanced LIGO layout by Haixing Miao.

Funding

F. Zhang is supported by the National Natural Science Foundation of China grants 12073005 and 12021003 and the Interdiscipline Research Funds of Beijing Normal University. M. Wang is supported by the Fundamental Research Funds for the Central Universities, grant no. 310432103.

Author information

Authors and Affiliations

Gravitational Wave and Cosmology Laboratory, Department of Astronomy, Beijing Normal University, Beijing, 100875, People’s Republic of China
Mengyao Wang & Fan Zhang
Advanced Institute of Natural Sciences, Beijing Normal University at Zhuhai, Zhuhai, 519087, People’s Republic of China
Fan Zhang

Contributions

F.Z. wrote the first two sections, and M.W. the remaining sections. Both authors read and approved the final manuscript.

Corresponding authors

Correspondence to Mengyao Wang or Fan Zhang.

Ethics declarations

Ethics approval and consent to participate

N/A

Consent for publication

N/A

Competing interests

The authors declare that they have no competing interests.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

 

[Source: https://link.springer.com/article/10.1007/s43673-023-00076-5]