1 Introduction

Currently, quantum information processing system is at its NISQ period, which is characterized with medium sized number of qubits, noisy gates, and short life time. Performing as many as possible quantum gates is extremely important in these devices. Typical NISQ devices include superconducting qubits and NV centers. One type of noise is the one caused by weak coupling with the environment. These noises are difficult to suppress using optimal control techniques. Since the decoupling operation will require the same length of time as the life time of the system. NV center is a typical system of that kind.

NV center is a defect consisting of a substitional nitrogen atom and adjacent vacancy in diamond. The spin state of NV center can be conveniently initialized and read-out with laser illumation [1] , and the triplet ground state can be coherently manipulated with resonant microwaves [2]. Nuclear spins around an NV center are also exploited as qubits [3]. The strong coupling nuclear spins, with distinguishable frequency splitting in optical detected magnetic resonance (ODMR) spectrum, can be manipulated with frequency-selective pulse. The NV center and nuclear spin system is a promising platform for quantum information processing [4, 5]. Many quantum algorithms [6, 7], quantum error corrections [8, 9], and quantum simulations [10] have been realized with NV center system. The system is an excellent platform for detecting ultra-weak magnetic fields [11,12,13].

There are many factors affecting the control performance in NV center system. Firstly, the thermal distribution and state-dependent evolution of the \(^{13}\)C nuclear spin bath are the major decoherence mechanisms of the NV electron spin in high purified diamond. The weak coupling spins, with coupling strength smaller than the inhomogeneous broadening, are selectively controlled with dynamic decoupling (DD) sequence filtering the unwanted spins. Secondly, the cross-talk between different nuclear spin states disturbs the control process in high-density ODMR spectrum. Thirdly, taking the real circumstance into consideration, the experimental factors, such as the microwave amplitude error and frequency detuning error, can also limit the control performance. To achieve high fidelity and robust control on these multi-qubit systems, many control methods [6, 14,15,16,17,18], suppression of phase noise in the of control hardware [19], topological dynamical decoupling [20], measurement-based feedback control [21], and holonomic gates [22], have been proposed and been tested in the experiments.

Quantum optimal control theory (OCT) has been extensively utilized to improve the control performance in multi-qubit systems. Gradient ascent pulse engineering (GRAPE) method [23] is widely used in magnetic resonance control. The cross-talk effect was suppressed with the OCT method [8, 16]. The robust OCT method, which is a multi-objective optimization, can suppress the quasi-static errors, such as the thermal noise and the control amplitude error, and prolong greatly the NV coherence time over \(T_2^*\) [7, 18]. Optimal control method can be combined with average Hamiltonian theory (AHT) to suppress the decoherence effect dynamically [24, 25] .

However, in NV-\(^{13}\)C weak coupling system, the required OCT control time can be much longer than both \(T_2^*\) of the NV electron spin and the period of the nuclear bath evolution [26]. At this time scale, the quasi-static assumption about the coupling noise is completely valid. An optimal control method that decouples the evolving bath is essential for multi-qubit control in such NV system, especially for the weak coupling case.

To accomplish the multi-qubit optimal control in NV center system, in particularly the weak-coupling system, we develop an efficient coupling-selective OCT (COCT), which decouples the system-environment and takes the evolution of the \(^{13}\)C bath into consideration. The optimization task of multi-qubit system in a long period can be divided into multiple tasks in smaller periods so as to further improve the effect. The method is experimentally tested in a NV-\(^{13}\)C weak-coupling system, and it has been shown that the lifetime has been prolonged significantly, and control rotation gate with five times of the phase decoherence time of NV qubit is completed with high fidelity.

2 The NV system

The ground state of a NV center is a spin triplet with \(m_s=0, \pm 1\). The \(m_s=-1\) and \(m_s=0\) states of the NV center are chosen as the \(|0\rangle\) and \(|1\rangle\) states of the electron qubit. The system is subject to a static magnetic field, and the Hamiltonian in the rotating frame is

\(\begin{aligned} \frac{H_{\text {NV}}(t)}{2\pi }=\Omega _x(t) I_x +\Omega _y(t) I_y \end{aligned}\)
(1)

where \(\Omega _{x/y}(t)\) is the Rabi frequency of the x/y component, and \(I_{x/y}=\sigma _{x/y}/2\) is the corresponding spin operator.

The \(^{13}\)C nuclear spins around the NV center interact through the electron spin with dipolar coupling. At the same time, the \(^{13}\)C nuclear spins precess in the static magnetic field, and

\(\begin{aligned} \frac{ H_{\text {NV-C}} + H_{\text {C}} }{2\pi } =|0\rangle \langle {0}| \otimes \sum\limits_i (\gamma ^i_x I^i_x +\gamma ^i_z I^i_z) + \sum\limits_i \omega _n^i I^i_z , \end{aligned}\)
(2)

where \(\gamma ^i_z\) (\(\gamma ^i_x\)) is the isotropic (anisotropic) coupling strength between the NV center and the ith nuclear spin, and \(\omega _n^i\) is the Zeeman splitting of the ith nuclear spin. The weak \(^{13}\)C-\(^{13}\)C interaction has been omitted in Eq.(2).

The \(^{13}\)C nuclear spin can be divided qubit nuclear spin (\(i \in \mathcal {S}\)) and the others (\(j \in \mathcal {B}\)) as the environment. The total Hamiltonian is

\(\begin{aligned} \frac{H(t)}{2\pi }= & {} \frac{H_{\text {NV}}(t) }{2\pi } +|0\rangle \langle {0}| \otimes \sum\limits_{i \in \mathcal {S}} (\gamma ^i_z I^i_z +\gamma ^i_x I^i_x)+\sum\limits_{i \in \mathcal {S}} \omega _n^i I^i_z \nonumber \\+ & {} |0\rangle \langle {0}| \otimes \sum\limits_{j \in \mathcal {B}} (\gamma ^j_z I^j_z +\gamma ^j_x I^j_x)+\sum\limits_{j \in \mathcal {B}} \omega _n^j I^j_z \end{aligned}\)
(3)

where \(\omega _n^i\) (\(\omega _n^j\)) is the Zeeman splitting of the ith ( jth ) nuclear spin.

The hyperfine interaction of the \(^{13}\)C bath can be represented as an effective field \(B_{\text {noise}}=\sum _{j \in \mathcal {B}} (\gamma ^j_x I^j_x+\gamma ^j_z I^j_z)\) applied on the electron spin. The fluctuation of this noise field results from both the thermal distribution and the dynamic evolution of the \(^{13}\) C bath.

2.1 OCT in the weak-coupling NV system

For the weak-coupling system, the needed control time is comparable to \(T_2\) time. In this time regime, bath evolution \(H_B=\sum _{j \in \mathcal {B}} \omega _n^j I^j_z\) fluctuates, and the robust OCT method, considering only the quasi-static thermal noise, fails. Here, we give a coupling selective OCT that is suited for quantum control in the weak-coupling system. The essential idea is to combine average Hamiltonian theory (AHT) and OCT so as to suppress unwanted coupling and strengthen the wanted coupling. We use the propagator method and expand it using a time-dependent expansion. Then, we optimize the target so as to achieve our goal of the optimal control.

(1) Propagator of target system

The system Hamiltonian is

\(\begin{aligned} H_S(t) = H_{NV}(t) +|0\rangle \langle {0}| \otimes \sum\limits_{i \in \mathcal {S}} (\gamma ^i_z I^i_z +\gamma ^i_x I^i_x)+\sum\limits_{i \in \mathcal {S}} \omega _n^i I^i_z \end{aligned}\)
(4)

The function to optimize is fidelity of the evolution defined as

\(\begin{aligned} F_S=\frac{\Vert {U_{w}}^{\dagger } \cdot U_S(T) \Vert ^{2}}{N_{D}^{\;2}} \end{aligned}\)
(5)

where \(U_S(t)=\mathbb {T} \cdot e^{-i \int _0^t H_S(t_1) dt_1}\) is the evolution of the target system, \(U_{w}\) is the objective quantum gate, and \(N_D\) is the dimension of the target system.

(2) System-bath coupling

The hyperfine interaction between the electron spin and the bath spins disturbs the propagator of the target system. We represent the subsystem composed of the target system and one \(^{13}\)C nuclear spin in the bath as

\(\begin{aligned} H_{SB}(t)=H_S(t) \otimes \mathbb {I}_2+|0\rangle \langle {0}| \otimes (\gamma _z I_z +\gamma _x I_x) +\mathbb {I}_S \otimes \omega _n I_z, \end{aligned}\)
(6)

where \(\mathbb {I}_2\) and \(\mathbb {I}_S\) are the identity operator in the nuclear spin and target system Hilbert space, respectively, and for the bath spin, the Ramsey frequency \(\omega _n\) approximated as \(\omega _0 = \gamma _n B\).

Taking the decoupled Hamiltonian as the reference

\(\begin{aligned} H_{\text {ref}}(t)=H_S(t) \otimes \mathbb {I}_2+\mathbb {I}_S \otimes \omega _0 I_z, \end{aligned}\)
(7)

and

\(\begin{aligned} H_{\text {SB}}(t)=H_{\text {ref}}(t) + H_{\text {c}}(t), \end{aligned}\)
(8)

the propagator Q in the toggling frame can be expanded as

\(\begin{aligned} Q= & {} \text {T} e^{-i \int [H_{\text {ref}}(t_1) + H_{\text {c}}(t_1)] dt_1} \nonumber \\= & {} \mathbb {I}_S \otimes \mathbb {I}_2-i\int _0^T \widetilde{U}(t_1)^\dagger \; H_{\text {c}} \; \widetilde{U}(t_1) dt_1 + \cdots , \end{aligned}\)
(9)

where the referenced propagator \(\widetilde{U}(t)=\mathbb {T} \cdot \text {exp} \left[ -i \int _0^t H_{\text {ref}}(s) ds \right]\), and the coupling term \(H_{\text {c}}=|0\rangle \langle {0}| \otimes (\gamma _z I_z +\gamma _x I_x) = (\mathbb {I}/2+I_z) \otimes (\gamma _z I_z +\gamma _x I_x)\).

(3) Decoupling optimization

To suppress the unwanted evolution of the target system, we should decouple the system and make Q to the form \(\mathbb {I}_S \otimes\)V , where V can be an operator in the bath space.

The decoupling optimization is performed from the lowest order of Q. The 1st order term disturbing the target system evolution is

\(\begin{aligned} Q_{x/z}=\int _0^T dt_1 \; \widetilde{U}(t_1)^\dagger \cdot I_z \otimes I_{x/z} \cdot \widetilde{U}(t_1) . \end{aligned}\)
(10)

To make Q into \(\mathbb {I}_S \otimes V\) form, we minimize the norm of \(Q_{x/z}\). The objective function is

\(\begin{aligned} \frac{ |\text {Tr}(U_{want}^\dagger \cdot U_S) |^{2} }{N_D^{\;2}} -\sum\limits_{k \in \{ x,z \}} \alpha _{k} \cdot \text {Tr}(Q_{k}^{\dagger } \cdot Q_{k}) \end{aligned}\)
(11)

where \(\alpha _{k}\) is the penalty parameter, and \(N_D\) is the dimension of the system subspace. The first part of the objective function is maximize to realize target evolution. The second part is minimized to decouple the bath. The objective function can be optimized with the gradient ascent method (see the Supplement).

Higher order decoupling method is given in the Supplement.

(4) Sub-sequence setting

By dividing the whole pulse sequence into many sub-sequences and decoupling in each sub-sequence, the decoupling performance can be further improved.

We divide the whole pulse sequence into N equal widths sub-sequences, and set the objective function as

\(\begin{aligned} \frac{ |\text {Tr}(U_{want}^\dagger \cdot U_S^N \cdots U_S^1) |^{2}}{N_D^{\;2}} -\sum\limits_{i=1}^N \sum\limits_{k\in \{ x,z \} } \alpha _{k} \cdot \Vert Q_{k}^{i \; \dagger } \cdot Q^i_{k}\Vert \end{aligned}\)
(12)

where \(U_S^{i}\) is the propagator in the ith sub-sequence ( \(\left[ (i-1)T/N, iT/N \right]\) ) and \(Q^{i}_k = \int _{(i-1)T/N}^{iT/N} dt_1 \; \widetilde{U}(t_1)^\dagger \cdot I_z \otimes I_{k} \cdot \widetilde{U}(t_1)\) is the corresponding term of perturbed propagator, and \(\alpha _{k}\) is the penalty parameter. The first part of the objective function make the total evolution \(U_S^N \cdots U_S^1\) approach target evolution. The optimization of second part decouples the bath in each subsequence.

After optimization, the system of the electron spin and the chosen \(^{13}\)C spin together realize objective propagator \(U_{w}\) . The unselected \(^{13}\)C spins will rotate independently, \(U^j = e^{-i [ (\omega _0+\gamma ^j_z /2) I_z + \gamma ^j_x/2 I_x ] \cdot T}\).

Because the optimization process needs only the algebra structure of the coupling term, the decoupling optimization is valid for every nuclear spin in the bath.

3 Experiment

We demonstrate the viability of the new COCT method in a weak-coupling NV-\(^{13}\)C system , illustrated in Fig. 1(a), experimentally. The NV center is in a type IIa diamond, with a 511 G static magnetic field applied on the [1 1 1] axis. The \(m_s=0\) and \(m_s=+1\) states constitute the electron qubit. The sample contains two distinguishable \(^{13}\)C nuclear spins as shown in Fig. 1(b). These nuclear spins can be detected by applying a dynamic decoupling sequence. Varying the delay time \(\tau\) between the \(\pi\) pulses, the two distinguishable coherence dips can be seen clearly, which reveal the existence of coupled nuclear spins. The fitted coupling strengths of these two nuclear spins are shown in Fig. 1(b), and they are much smaller than the measured inhomogeneous broadening \(\Delta \approx 380\) kHz.

Using the COCT method, we realized the NV-\(^{13}\)C control, such as the iSWAP\(^\dagger\) gates, the Control-\(R_{\pm x}^{\phi }\) gates. We illustrate the performance of NV-C\(_1\) gates in the main text, and the results of NV-C\(_2\) control are shown in the Supplement material. Utilizing these 2-qubit gates, we prepared an entanglement state on the two nuclear spins. We present them in the following.

(1) iSWAP\(^\dagger\) gate

An iSWAP\(^\dagger\) gate swaps the quantum state of the electron spin and the nuclear spin, the matrix representation is

\(\begin{aligned} \text {iSWAP}^{\dagger } =\left( \begin{array}{llll} 1 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} -i &{} 0\\ 0 &{} -i &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 1\\ \end{array} \right) \end{aligned}\)
(13)

The optimized NV-\(C_1\) iSWAP\(^\dagger\) gate consists of 30 decoupled sub-sequences, each with the same shape, the waveforms are shown in Fig. 2(a), (b). The total length of the pulse sequence is 30 \(\times\) 5675 ns = 170.25 \(\mu\)s, which is comparable to the phase decoherence time \(T_2=203 \; \mu\)s.

In order to test the selectivity of the searched pulse sequence, we simulated the pulse sequence on a system with various values of \(\gamma _x\) and \(\gamma _z\) parameters. The simulation results are illustrated in Fig. 2(d), (e). We simulated the two-qubit system with a weak coupling with the following Hamiltonian

\(\begin{aligned} H(t, \gamma _x, \gamma _z)=H_{\text {NV}}(t)+S_z \otimes (\gamma _z I_z+\gamma _x I_x) +\omega _0 I_z , \end{aligned}\)
(14)

where \(H_{\text {NV}}(t)\) changes as the optimized sequence. The fidelities between the simulated propagators and the iSWAP\(^\dagger\) gate (the propagator \(\text {I}_2 \otimes e^{-i [ (\omega _0+\gamma _z /2) I_z + \gamma _x/2 I_x ] \cdot T}\)) are represented as different colors in (a) ((b)).

The iSWAP\(^\dagger\) gate is a widely used gate for state preparation and readout measurement. The performance of this iSWAP\(^\dagger\) gate is tested in the nuclear Ramsey experiment (Fig. 2(f)). By preparing the electron spin in 0 state and the nuclear spin in a superposition state, the nuclear spin processes at a frequency of \(\omega _0 \approx \gamma _n B\). At last, the nuclear state is swapped to the electron spin for the readout (Fig. 2(c)).

(2) Control-\(\textrm{R}_{\pm x}^{\phi }\) gate

Another important two-qubit gate is the Control-\(\text {R}_{\pm x}^{\phi }\) gate, which can be described as

\(\begin{aligned} \text {C-R}_{\pm x}^{\phi } =\left( \begin{array}{cc} e^{-i I_x \phi } &{} 0\\ 0 &{} e^{+i I_x \phi } \end{array} \right) \end{aligned}\)
(15)

The optimized pulse sequence for each C-\(\text {R}_{\pm x}^{\pi /28}\) gate lasts for 5670 ns. At the same time, the C-\(\text {R}_{\pm x}^{\pi /2}\) gate consisting of 14 C-\(\text {R}_{\pm x}^{\pi /28}\) gates is also optimized. The waveforms of the pulse sequences are shown in Fig. 2(c), (d) of Supplement.

We also demonstrated the selectivity of the C-\(\text {R}_{\pm x}^{\pi /2}\) gate using numerical simulations, in Fig. 3(a), (b). The drast selectivity of the isotropic coupling strength \(\gamma _z\) guarantees the coherence keeping capability of the pulse sequence.

The coherence protection capability of the COCT is demonstrated in experiment shown in Fig. 3(c). Preparing the electron spin in superposition state \(\frac{1}{\sqrt{2}} ( |0\rangle +|1\rangle )\), and performing C-\(\text {R}_{\pm x}^{\pi /28}\) gates successively, we can observe the oscillation of the electron coherence (Fig. 3(d)). The electron spin coherence is kept over 1.02(8) ms, which is 5 times longer than the phase coherence time \(T_2 \approx 203 \; \mu s\).

Utilizing the iSWAP\(^\dagger\) gate for the state preparation and readout of the nuclear spin, we can observe the nuclear rotation with the C-\(\text {R}_{\pm x}^{\pi /28}\) gates application (Fig. 3(e)). The nuclear spin rotates along opposite directions under different electron spin states in the experiment (Fig. 3(f)).

Fig. 1
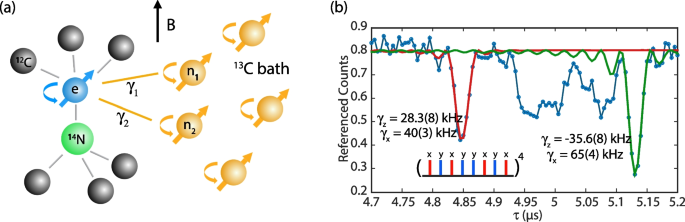
figure 1

(a) The schematic of the 3 qubits system. The two detectable weak coupling \(^{13}\)Cs are taken as qubits. And the rest nuclear spins are taken as an environment, which should be decoupled during the control process. (b) The coherence of the NV electron spin as a function of \(\tau\) in DD sequence. The green (red) line is the simulated curve with the 1st (2nd) nuclear parameters


Fig. 2
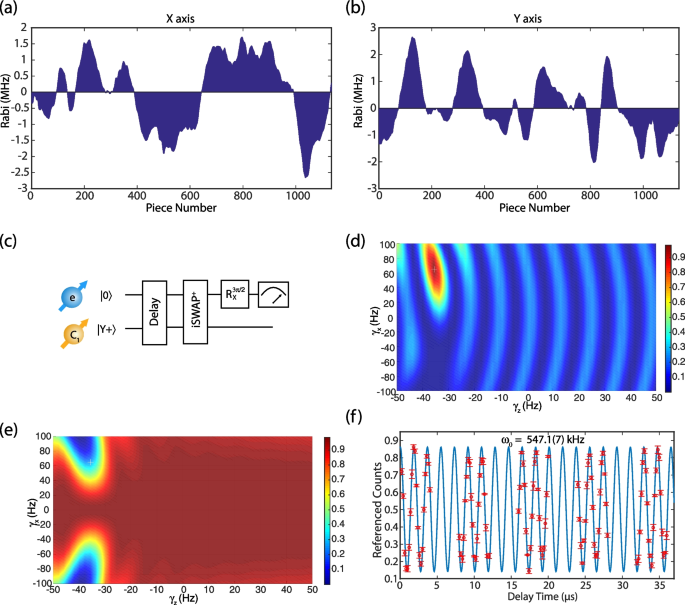
figure 2

COCT pulse sequence and experimental demonstration of the iSWAP gate. (a) A \(\Omega _x\) sub-sequence of the COCT pulse sequence for the iSWAP gate. (b) The same as (a) for \(\Omega _y\). (c) Circuit for nuclear Ramsey experiment using iSWAP gate. Initially, electron spin in \(|0\rangle\) and nuclear spin is in \(\frac{1}{\sqrt{2}} (|0\rangle +|1\rangle ) = |X+\rangle\). After delay \(\tau\), nuclear spin evolves into \(cos \theta |0\rangle +sin \theta |1\rangle\). iSWAP gate transfer the nuclear spin state into the electron spin, and then is measured. (d) Selectivity test of the COCT sequence. The fidelity of the iSWAP gate. It reaches its maximum at the experimental value of \(\gamma _x\)= 65 kHz, \(\gamma _z\)= − 35.6 kHz (with crosspoint). (e) For system without the weak-coupling, the same COCT pulse sequence does not suppress the unwanted evolution, the fidelity remains high most of the time. (f) Ramsey precession experiment. ISWAP successfully swap the state of nuclear spin to the electron spin. The Ramsey oscillation is clearly demonstrated in the experiment


Fig. 3
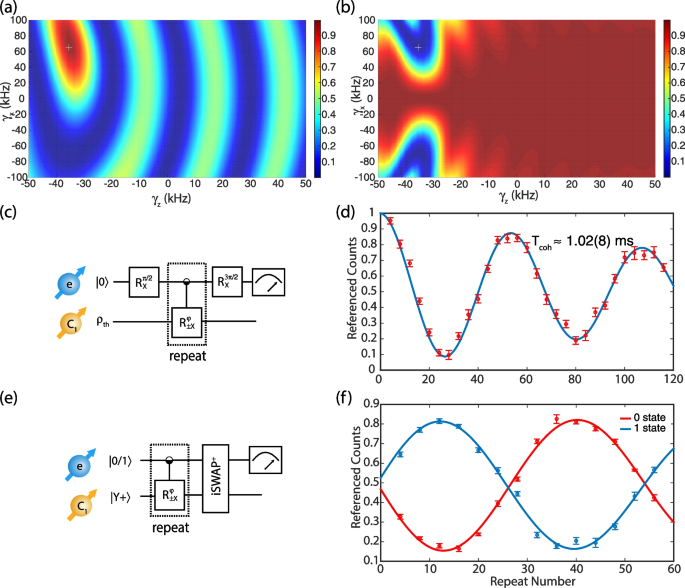
figure 3

Numerical simulation and experimental demonstration of the C-\(\text {R}^{\pi }_{\pm x}\) gate. (a), (b) The simulation to demonstrate the selectivity of the C-\(\text {R}^{\pi }_{\pm x}\) gate. The isotropic (anisotropic) coupling strength increases along x (y) axis. The fidelity between the simulated propagator and the objective propagator (the independent propagator) is represented as different colors in (a) (b). The white cross is the objective coupling strength of the NV-\(C_1\) C-\(\text {R}^{\pi }_{\pm x}\) gate. The selected range of isotropic coupling \(\gamma _z\) is about 10 kHz. (c) The diagram to test the capability of coherence keeping of the C-\(\text {R}^{\phi }_{\pm x}\) gate. We prepare the electron spin in superposition state and apply C-\(\text {R}^{\phi }_{\pm x}\) gates repeatedly. (d) The coherence of the NV electron spin as a function of the gate number. The fitted coherence time is about 1.02 ms. (e) The diagram to observe the nuclear rotation with C-\(\text {R}^{\phi }_{\pm x}\) gates applied. By preparing the electron spin in different states, the nuclear spin rotates along opposite axis with the application of the C-\(\text {R}^{\phi }_{\pm x}\) gates. The superposition state on C\(_1\) is prepared with similar method in Fig.2(c). (f) The nuclear rotation under repetitively applying the C-\(\text {R}^{\phi }_{\pm x}\) gate, with different electron states. The red (blue) points are the result with electron spin in \(m_s=0\) (\(m_s=+1\)) state


4 Discussion

We realized optimal control in weak coupling system for the first time. In our optimization, the hyperfine interaction between the evolving bath and the central spin is decoupled. The performance of the new method is demonstrated in experiments. The advantages of the new method are being a high fidelity control and the robustness to quasi-static noise, of the optimal control is inherited by the new method.

The radio frequency field can also be applied to manipulate the nuclear spins directly. In this work, the flip-flop between \(^{13}\)C spins has been ignored for the small dipolar interaction. With the applied radio frequency field, the decoupling of the \(^{13}\)C-\(^{13}\)C interaction can also be introduced into the optimization.

The performance of the optimized pulse sequence can be further improved with the feedback control [18]. As the low temperature can extend the coherence time of the NV electron spin [27, 28], the experiments in low temperature should be greatly improved.

The COCT method which presented here is universal, and it can also be extended to other weak-coupling quantum systems. Recently, quantum optimal control is applied in quantum sensing application, especially in NV system. The COCT method can also be applied in this area.