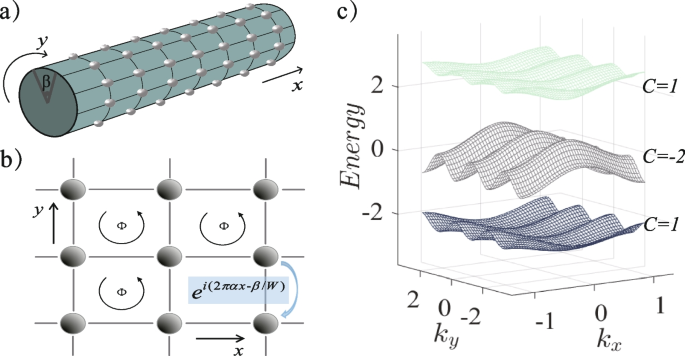
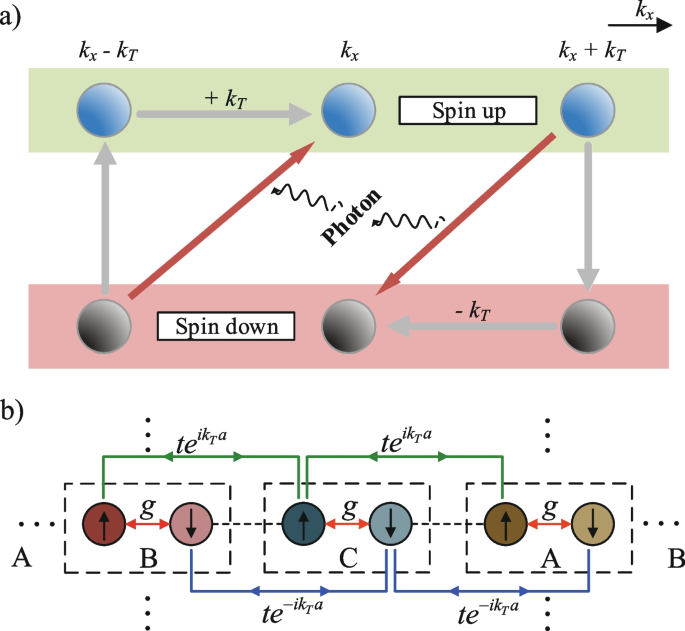
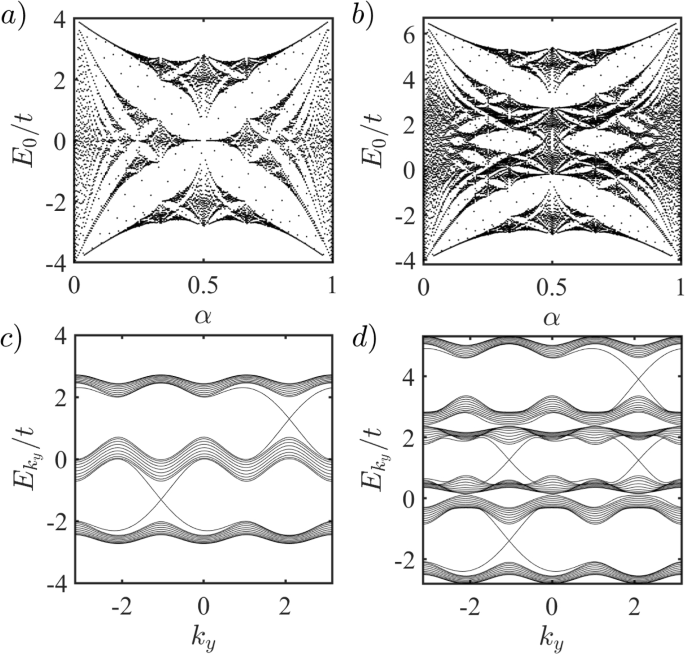
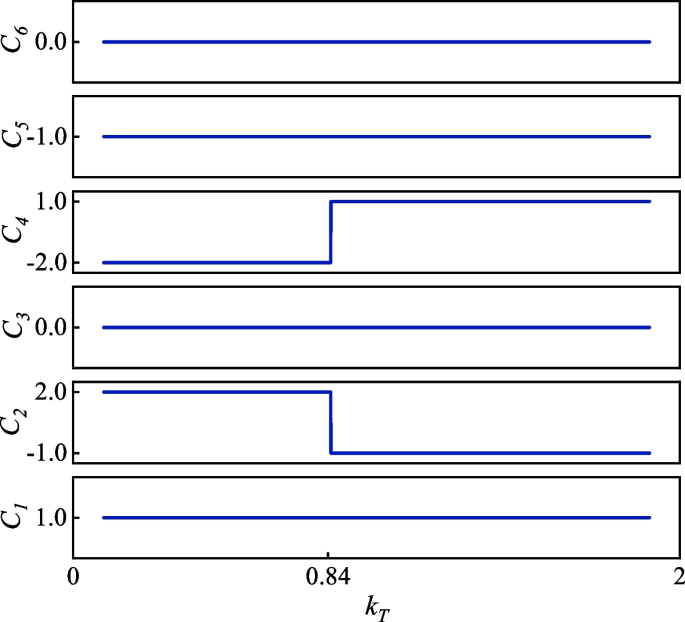
-
K.V. Klitzing, G. Dorda, M. Pepper, New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance. Phys. Rev. Lett. 45, 494 (1980)
-
C.-K. Chiu, J.C.Y. Teo, A.P. Schnyder, S. Ryu, Classification of topological quantum matter with symmetries. Rev. Mod. Phys. 88, 035005 (2016)
-
C.L. Kane, E.J. Mele, Quantum Spin Hall Effect in Graphene. Phys. Rev. Lett. 95, 226801 (2005)
-
C.L. Kane, E.J. Mele, \({Z}_{2}\) Topological Order and the Quantum Spin Hall Effect. Phys. Rev. Lett. 95(2005)
-
B.A. Bernevig, T.L. Hughes, S.-C. Zhang, Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 314, 1757 (2006)
-
M.Z. Hasan, C.L. Kane, Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045 (2010)
-
X.-L. Qi, S.-C. Zhang, Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057 (2011)
-
F.D.M. Haldane, Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the “Parity Anomaly’’. Phys. Rev. Lett. 61, 2015 (1988)
-
X.-L. Qi, Y.-S. Wu, S.-C. Zhang, Topological quantization of the spin Hall effect in two-dimensional paramagnetic semiconductors. Phys. Rev. B 74, 085308 (2006)
-
T. Neupert, L. Santos, C. Chamon, C. Mudry, Fractional Quantum Hall States at Zero Magnetic Field. Phys. Rev. Lett. 106, 236804 (2011)
-
K. Sun, Z. Gu, H. Katsura, S. Das Sarma, Nearly Flatbands with Nontrivial Topology. Phys. Rev. Lett. 106, 236803 (2011)
-
E. Tang, J.-W. Mei, X.-G. Wen, High-Temperature Fractional Quantum Hall States. Phys. Rev. Lett. 106, 236802 (2011)
-
P. Hauke, M. Lewenstein, A. Eckardt, Tomography of Band Insulators from Quench Dynamics. Phys. Rev. Lett. 113, 045303 (2014)
-
D.-L. Deng, S.-T. Wang, L.-M. Duan, Direct probe of topological order for cold atoms. Phys. Rev. A 90, 041601 (2014)
-
A. Iurov, G. Gumbs, D. Huang, Peculiar electronic states, symmetries, and Berry phases in irradiated \(\alpha -{\mathrm{T}}_{3}\) materials. Phys. Rev. B 99(2019)
-
F.L.N. Santos, M.A. Caracanhas, M.C.O. Aguiar, R.G. Pereira, Bound states in two-dimensional Fermi systems with quadratic band touching. Phys. Rev. B 101, 155120 (2020)
-
X.-X. Zhang, T.T. Ong, N. Nagaosa, Theory of photoinduced Floquet Weyl semimetal phases. Phys. Rev. B 94, 235137 (2016)
-
T. Yoshida, K. Kudo, H. Katsura, Y. Hatsugai, Fate of fractional quantum Hall states in open quantum systems: Characterization of correlated topological states for the full Liouvillian. Phys. Rev. Research 2, 033428 (2020)
-
M.D. Caio, N.R. Cooper, M.J. Bhaseen, Quantum Quenches in Chern Insulators. Phys. Rev. Lett. 115, 236403 (2015)
-
J.H. Wilson, J.C.W. Song, G. Refael, Remnant Geometric Hall Response in a Quantum Quench. Phys. Rev. Lett. 117, 235302 (2016)
-
A. Rivas, O. Viyuela, M.A. Martin-Delgado, Density-matrix Chern insulators: Finite-temperature generalization of topological insulators. Phys. Rev. B 88, 155141 (2013)
-
D.P. Pires, D.O. Soares-Pinto, E. Vernek, Dynamics of quantum resources in regular and Majorana fermion systems. Phys. Rev. A 105, 042407 (2022)
-
H.Z. Shen, H. Li, Y.F. Peng, X.X. Yi, Mechanism for Hall conductance of two-band systems against decoherence. Phys. Rev. E 95, 042129 (2017)
-
S. Xu, H.Z. Shen, X.X. Yi, Current in an open tight-binding system. Phys. Rev. A 99, 012102 (2019)
-
V.V. Albert, B. Bradlyn, M. Fraas, L. Jiang, Geometry and Response of Lindbladians. Phys. Rev. X 6, 041031 (2016)
-
T. Oka, H. Aoki, Photovoltaic Hall effect in graphene. Phys. Rev. B 79, 081406 (2009)
-
O.V. Kibis, Metal-insulator transition in graphene induced by circularly polarized photons. Phys. Rev. B 81, 165433 (2010)
-
O.V. Kibis, O. Kyriienko, I.A. Shelykh, Band gap in graphene induced by vacuum fluctuations. Phys. Rev. B 84, 195413 (2011)
-
A. Camacho-Guardian, N. Goldman, P. Massignan, G.M. Bruun, Dropping an impurity into a Chern insulator: A polaron view on topological matter. Phys. Rev. B 99, 081105 (2019)
-
M.V. Durnev, S.A. Tarasenko, High-Frequency Nonlinear Transport and Photogalvanic Effects in 2D Topological Insulators. Ann. Phys. 531, 1800418 (2019)
-
R. Wang, B. Wang, R. Shen, L. Sheng, D.Y. Xing, Floquet Weyl semimetal induced by off-resonant light. EPL 105, 17004 (2014)
-
S. Vajna, B. Horovitz, B. Dóra, G. Zaránd, Floquet topological phases coupled to environments and the induced photocurrent. Phys. Rev. B 94, 115145 (2016)
-
L. Bucciantini, S. Roy, S. Kitamura, T. Oka, Emergent Weyl nodes and Fermi arcs in a Floquet Weyl semimetal. Phys. Rev. B 96, 041126 (2017)
-
J.C. Budich, P. Zoller, S. Diehl, Dissipative preparation of Chern insulators. Phys. Rev. A 91, 042117 (2015)
-
Y. Hu, P. Zoller, J.C. Budich, Dynamical Buildup of a Quantized Hall Response from Nontopological States. Phys. Rev. Lett. 117, 126803 (2016)
-
W. Nie, M. Antezza, Y.-X. Liu, F. Nori, Dissipative Topological Phase Transition with Strong System-Environment Coupling. Phys. Rev. Lett. 127, 250402 (2021)
-
T. Morimoto, Y. Hatsugai, H. Aoki, Optical Hall Conductivity in Ordinary and Graphene Quantum Hall Systems. Phys. Rev. Lett. 103, 116803 (2009)
-
J.G. Pedersen, M.H. Brynildsen, H.D. Cornean, T.G. Pedersen, Optical Hall conductivity in bulk and nanostructured graphene beyond the Dirac approximation. Phys. Rev. B 86, 235438 (2012)
-
H. Dehghani, A. Mitra, Optical Hall conductivity of a Floquet topological insulator. Phys. Rev. B 92, 165111 (2015)
-
T. Morimoto, Y. Hatsugai, H. Aoki, Optical Hall conductivity in 2DEG and graphene QHE systems. Physica E 42, 751 (2010)
-
N.H. Lindner, G. Refael, V. Galitski, Floquet topological insulator in semiconductor quantum wells. Nat. Phys. 7, 490 (2011)
-
T. Kitagawa, E. Berg, M. Rudner, E. Demler, Topological characterization of periodically driven quantum systems. Phys. Rev. B 82, 235114 (2010)
-
B. Gulácsi, B. Dóra, From Floquet to Dicke: Quantum Spin Hall Insulator Interacting with Quantum Light. Phys. Rev. Lett. 115, 160402 (2015)
-
P.G. Harper, Single Band Motion of Conduction Electrons in a Uniform Magnetic Field. Proc. Phys. Soc. Sect. A 68, 874 (1955)
-
D.R. Hofstadter, Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 14, 2239 (1976)
-
M. Aidelsburger, M. Atala, M. Lohse, J.T. Barreiro, B. Paredes, I. Bloch, Realization of the Hofstadter Hamiltonian with Ultracold Atoms in Optical Lattices. Phys. Rev. Lett. 111, 185301 (2013)
-
C.J. Kennedy, W.C. Burton, W.C. Chung, W. Ketterle, Observation of Bose Einstein Condensation in a strong synthetic magnetic field. Nat. Phys. 11, 859 (2015)
-
F. Mivehvar, H. Ritsch, F. Piazza, Superradiant Topological Peierls Insulator inside an Optical Cavity. Phys. Rev. Lett. 118, 073602 (2017)
-
J.-S. Pan, X.-J. Liu, W. Zhang, W. Yi, G.-C. Guo, Topological Superradiant States in a Degenerate Fermi Gas. Phys. Rev. Lett. 115, 045303 (2015)
-
G. Ehlers, S.R. White, R.M. Noack, Hybrid-space density matrix renormalization group study of the doped two-dimensional Hubbard model. Phys. Rev. B 95, 125125 (2017)
-
J. Motruk, M.P. Zaletel, R.S.K. Mong, F. Pollmann, Density matrix renormalization group on a cylinder in mixed real and momentum space. Phys. Rev. B 93, 155139 (2016)
-
L. Stenzel, A.L.C. Hayward, C. Hubig, U. Schollwöck, F. Heidrich-Meisner, Quantum phases and topological properties of interacting fermions in one-dimensional superlattices. Phys. Rev. A 99, 053614 (2019)
-
L. Stenzel, A.L.C. Hayward, U. Schollwöck, F. Heidrich-Meisner, Topological phases in the Fermi-Hofstadter-Hubbard model on hybrid-space ladders. Phys. Rev. A 102, 023315 (2020)
-
Q. Niu, D.J. Thouless, Y.-S. Wu, Quantized Hall conductance as a topological invariant. Phys. Rev. B 31, 3372 (1985)
-
W. Nie, T. Shi, F. Nori, Y.-X. Liu, Topology-Enhanced Nonreciprocal Scattering and Photon Absorption in a Waveguide. Phys. Rev. Appl. 15, 044041 (2021)
-
M.J. Kastoryano, M.S. Rudner, Topological transport in the steady state of a quantum particle with dissipation. Phys. Rev. B 99, 125118 (2019)
-
G.-W. Lin, M.-Y. Ye, L.-B. Chen, Q.-H. Du, X.-M. Lin, Generation of the singlet state for three atoms in cavity QED. Phys. Rev. A 76, 014308 (2007)
-
E. G. Dalla Torre, J. Otterbach, E. Demler, V. Vuletic, M. D. Lukin, Dissipative Preparation of Spin Squeezed Atomic Ensembles in a Steady State. Phys. Rev. Lett. 110, 120402 (2013)
-
Y. Deng, J. Cheng, H. Jing, S. Yi, Bose-Einstein Condensates with Cavity-Mediated Spin-Orbit Coupling. Phys. Rev. Lett. 112, 143007 (2014)
-
M. Aidelsburger, M. Lohse, C. Schweizer, M. Atala, J.T. Barreiro, S. Nascimbne, N.R. Cooper, I. Bloch, N. Goldman, Measuring the Chern number of Hofstadter bands with ultracold bosonic atoms. Nat. Phys. 11, 162 (2015)
-
H. Miyake, G.A. Siviloglou, C.J. Kennedy, W.C. Burton, W. Ketterle, Realizing the Harper Hamiltonian with Laser-Assisted Tunneling in Optical Lattices. Phys. Rev. Lett. 111, 185302 (2013)
-
A. González-Tudela, C.S. Muñoz, J.I. Cirac, Engineering and Harnessing Giant Atoms in High-Dimensional Baths: A Proposal for Implementation with Cold Atoms. Phys. Rev. Lett. 122, 203603 (2019)
-
M. Lipka, M. Parniak, Single-Photon Hologram of a Zero-Area Pulse. Phys. Rev. Lett. 126, 063601 (2021)
-
D.J. Thouless, M. Kohmoto, M.P. Nightingale, M. den Nijs, Quantized Hall Conductance in a Two-Dimensional Periodic Potential. Phys. Rev. Lett. 49, 405 (1982)
-
M. Kohmoto, Topological invariant and the quantization of the Hall conductance. Ann. Phys. 160, 343 (1985)
-
T. Fukui, Y. Hatsugai, H. Suzuki, Chern Numbers in Discretized Brillouin Zone: Efficient Method of Computing (Spin) Hall Conductances. J. Phys. Soc. Jpn. 74, 1674 (2005)
-
Y.-S. Wu, Lectures on Topological Aspects of the Quantum Hall Effect, edited by H.C. Lee, Physics, Geometry and Topology (Plenum Press, New York, 1990), pp.461–491
-
Y. Yang, Z. Xu, L. Sheng, B. Wang, D.Y. Xing, D.N. Sheng, Time-Reversal-Symmetry-Broken Quantum Spin Hall Effect. Phys. Rev. Lett. 107, 066602 (2011)
-
W. Beugeling, N. Goldman, C.M. Smith, Topological phases in a two-dimensional lattice: Magnetic field versus spin-orbit coupling. Phys. Rev. B 86, 075118 (2012)
-
C. Hofrichter, L. Riegger, F. Scazza, M. Höfer, D.R. Fernandes, I. Bloch, S. Fölling, Direct Probing of the Mott Crossover in the SU(N) Fermi-Hubbard Model. Phys. Rev. X 6, 021030 (2016)