Introduction
In 1935, a famous argument was presented by Einsten, Podolsky, and Rosen to support the incompleteness of quantum physics [1]. In this argument, the correlations of a two-partical state allow that the results of these measures on one object are predicted by the other one measured via preforming the same measurements. Quantum correlations between different objects are crucial for the incompleteness of quantum physics. The wave function of one object can be influenced by another one utilizing the suitable measurements, which is called quantum steering by Schrödinger for this phenomenon, while his early works were not widely noticed at that time [2]. In recent years, this quantum correlations has attracted intense interest from physicists according to the properties of quantum steering in quantum information theory [3, 4]. In the modern view, the conditional states can not be described by a local hidden state model on an object. Therefore, quantum steering represents a quantum correlation situated between entanglement and Bell nonlocality [5, 6]. With the rapid development of the theory of steering, quantum steering shows a natural formulation for quantum information processing [7,8,9], and its concept helps to understand and solve the open questions in quantum physics [10]. Different from quantum entanglement and Bell nonlocality, quantum steering has two different directions between the objects involved, and the steerability in the two different directions can be unequal. According to the definition of quantum steering, the asymmetry between two objects leads to a question naturally arising, i.e., whether there is a state where the one-way steerability exists between two objects [11]. By taking advantage of the antisymmetric nature of quantum steering, various information protocols that rely on entanglement have additional security, such as one-side device-independent quantum key distribution, directional quantum communication and computing [12].
One-way steerable states were studied and demonstrated by the continuous variable systems [13,14,15] and the discrete systems [16,17,18,19,20,21,22]. Moreover, the one-way quantum steering also attracted intense attention from experimental physicists in recent years [23,24,25,26,27,28,29]. As a special class of continuous variable scenarios, the characterization of steerable state was originally stated in Gaussian systems [11, 30]. Unlike other steering scenarios, the steerability in Gaussian regime can be easily evaluated via an inequality, and monogamy relations for multipartite steering can also be proved [31,32,33,34]. The steerable states have been generated to verify the fundamental principles of quantum mechanics in various macroscopic quantum systems [35,36,37,38,39,40]. Recently, asymmetric steering can be achieved between two completely symmetric magnon modes via a hybrid ferrimagnet-light system [41]. Moreover, the one-way quantum steering can also be generated between two mechanical modes using four-tone driving laser in a modulated optomechanical system [42]. In 2021, the reservoir-engineered entanglement can be significantly enhanced by a nondegenerate parametric amplifier (NDPA) and an auxiliary cavity in a cascaded bosonic system [43].
In this paper, we investigate the Gaussian steering for a generic optomechanical system with three bosonic modes, in which the optomechanical interaction exists between the mechanical oscillator and the auxiliary optical mode, and the beam-splitter interaction and parametric interaction with different strengths exist between the two optical modes. We find that the strong and stable Gaussian steering can be achieved and enhanced between the mechanical mode and the auxiliary optical mode without direct interaction. Benefiting for the existence of NDPA, the main optical mode and the delocalized Bogoliubov modes can be cooled effectively, which results in significantly enhanced entanglement and steering between the mechanical mode and the auxiliary optical mode. Moreover, we observe that the Gaussian steering in the two directions from the mechanical mode to the auxiliary optical mode as well as from the auxiliary optical mode to the mechanical mode can be adjusted by the damping rate of the auxiliary optical mode. Therefore, the one-way Gaussian steering in the system can be easily implemented in an appropriate parameter regime.
System Hamiltonian and dynamical equations
As schematically shown in Fig. 1, we consider a model as a three-mode cavity optomechanical system, which contains two nondegenerate optical modes and a mechanical resonator. There are the beam-splitter-type interaction and the two-mode parametric-down-converted-type interaction between two optical cavity modes. The main optical mode 1 is coupled to a mechanical resonator and driven by a red-detuned control field with frequency \(\omega _l\) and strength E. The Hamiltonian of the system is given by \((\hbar =1)\)
where \(a_j\) is the annihilation operator in optical mode j with frequency \(\omega _j\) \((j=1,2)\). The mechanical resonator b is coupled with optical mode \(a_1\) by radiation pressure force, which possesses frequency \(\omega _m\) and damping rate \(\gamma _m\). The vacuum single-photon optomechanical coupling \(g=\omega _1/L(\sqrt{\hbar /m\omega _m})\) in optical mode \(a_1\), in which L and m are the length of the cavity and the mass of the mechanical resonator, respectively. There is the beam-splitter interaction between two optical modes via photon hopping with the coupling rate J. Furthermore, the NDPA is driven by a laser with frequency \(\omega _p\) and gain \(\lambda\), which is achieved by the pairs of parametric-down-converted nondegenerate photons resonant with the two optical cavities. In the frame rotating at the driving laser frequency \(\omega _l\), the effective Hamiltonian of the system is given by
where \(\Delta _1'=\omega _1-\omega _l\) \((\Delta _2=\omega _2-\omega _l)\) is the main (auxiliary) optical mode 1(2) detuning with respect to external driving laser, and we assume \(\omega _p=2\omega _l\). The quantum Langevin equations of the system are
where \(\kappa _{1(2)}\) and \(\gamma _m\) are the loss rates for the optical mode \(a_1(a_2)\) and the mechanical resonator, respectively, corresponding to noise operators \(a^{\mathrm {in}}_{1(2)}\) and \(b^{\mathrm {in}}\) with zero mean associated with the dissipations, which have nonzero correlation functions \(\langle a_{1(2)}^{\mathrm {in}}(t) a_{1(2)}^{\mathrm {in},\dagger }(t')\rangle = \delta (t-t')\), \(\langle b^{\mathrm {in}}(t)b^{\mathrm {in},\dagger }(t')\rangle =(\bar{n}_m+1)\delta (t-t')\), and \(\langle b^{\mathrm {in},\dagger }(t)b^{\mathrm {in}}(t')\rangle =\bar{n}_m\delta (t-t')\), in which \(\bar{n}_m=[\text {exp}(\hbar \omega _m/k_BT)-1]^{-1}\) is mean thermal phonon number of the mechanical mode at environmental temperature T and \(k_B\) is the Boltzmann constant. When the system is stable, we can linearize the system dynamics by writing \(a_{1(2)}=a_{s1(s2)}+\delta a_{1(2)}\) and \(b=b_s+\delta b\), where \(a_{s1(s2)}\) and \(b_s\) are the steady-state mean values, and \(\delta a_{1(2)}\) and \(\delta b\) are the quantum fluctuation operators around the steady-state mean values, respectively. In the following, the corresponding linearized Langevin equations and Hamiltonian for quantum fluctuation operators can be readily rewritten as
and
where \(\Delta _1=\Delta _1'+g(b_s+b_s^*)\), and \(G=ga_{s1}\) is the linearized optomechanical coupling strength, which can be assumed as real by appropriately adjusting the driving laser phase. Now by defining the quadratures \(\delta X_{1(2)}=(\delta a_{1(2)}+\delta a_{1(2)}^\dagger )/\sqrt{2}\), \(\delta P_{1(2)}=(\delta a_{1(2)}-\delta a_{1(2)}^\dagger )/\sqrt{2}i\), \(\delta X_b=(\delta b+\delta b^\dagger )/\sqrt{2}\), and \(\delta P_b=(\delta b-\delta b^\dagger )/\sqrt{2}i\), then above linearized Langevin equations (i.e., Eq. (4)) can be rewritten as the compact matrix form
where \(\delta u(t)=(\delta X_1, \delta P_1, \delta X_2, \delta P_2, \delta X_b, \delta P_b)^T\) is the vector of continuous-variable fluctuation operators, and \(u^{\mathrm {in}}(t)=(X_1^{\mathrm {in}}, P_1^{\mathrm {in}}, X_2^{\mathrm {in}}, P_2^{\mathrm {in}}, X_b^{\mathrm {in}}, P_b^{\mathrm {in}})^T\) is the corresponding vector of noise, in which \(X_{1(2)}^{\mathrm {in}}=( a_{1(2)}^{\mathrm {in}}+ a_{1(2)}^{\mathrm {in},\dagger })/\sqrt{2}\), \(P_{1(2)}^{\mathrm {in}}=(a_{1(2)}^{\mathrm {in}}- a_{1(2)}^{\mathrm {in},\dagger })/\sqrt{2}i\), \(X_b^{\mathrm {in}}=(b^{\mathrm {in}}+ b^{\mathrm {in},\dagger })/\sqrt{2}\), and \(P_b^{\mathrm {in}}=(b^{\mathrm {in}}- b^{\mathrm {in},\dagger })/\sqrt{2}i\). Moreover, the time-independent drift matrix A can be written as
The system is stable when all the eigenvalues of the drift matrix A have negative real parts. The general stability condition is associated with the Routh-Hurwitz criterion. Next, we only consider the parameter conditions of the system under the stability regime. The steady state of the system is in the Gaussian state when the input quantum noises are Gaussian. The covariance matrix V can be fully characterized by the following Lyapunov equation as
where the covariance matrix V is \(6\times 6\) matrix, and D is diffusion matrix, in which the matrix elements are derived by
Based on the nonzero correlation functions of the noise operators, one can obtain
and the covariance matrix of the system can be written as
where each matrix element is \(2\times 2\) block matrix. The block \(V_{a1(a2,b)}\) indicates the variance within subsystem \(a_1(a_2,b)\), while the blocks on the off-diagonal are the covariance between two different subsystems, which indicates the entanglement property between the corresponding subsystems. To evaluate the pairwise entanglement, we consider a reduced \(4\times 4\) covariance submatrix
The bipartite entanglement can be evaluated by logarithmic negativity
where
To evaluate the Gaussian steering, we consider the computable measure in Ref. [44] for arbitrary bipartite Gaussian states. The steering in the direction from mode k to l is quantified by
with \(S(\sigma )=\frac{1}{2}\)ln det\(\sigma\) being the R\(\mathrm {e}\)nyi-2 entropy. The larger value of \(\mathcal {G}\) implies stronger Gaussian steerability.
Analysis and discussion
The steady-state optomechanical entanglement between modes \(a_2\) and b can be realized with the optomechanical interaction G between modes \(a_1\) and b and the tunneling interaction J between modes \(a_1\) and \(a_2\). The decay rate of the optical cavity can be implemented over a wide range of parameters, since the maximum optical fineness can be reached to \(10^{10}\) experimentally [45]. The parametric-down-conversion-type interaction can produce nondegenerate photon pairs \(a_1^\dagger a_2^\dagger\) by driving NDPA [46].
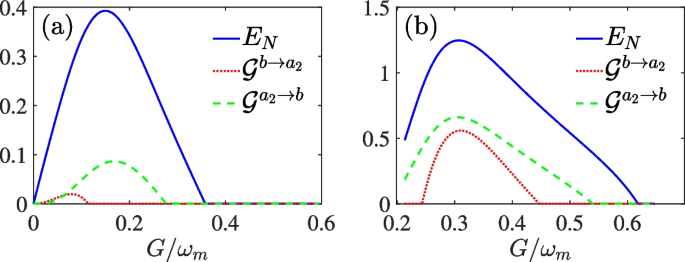
The steady-state optomechanical entanglement \(E_N(b,a_2)\) and steering parameters \(\mathcal {G}^{b\rightarrow a_2}\) and \(\mathcal {G}^{a_2\rightarrow b}\) versus the optomechanical coupling strength G for a \(\lambda =0\) and b \(\lambda =0.2\omega _m\). The other parameters are \(\Delta _1=-\Delta _2=\omega _m\), \(\kappa _1=0.9\omega _m\), \(\kappa _2=\gamma _m=0.01\omega _m\), and \(J=0.5\omega _m\)
We plot Fig. 2 to clearly illustrate the effects of NDPA on the optomechanical entanglement and Gaussian steering. As shown in Fig. 2a, we show the steady-state optomechanical entanglement between modes b and \(a_2\) and the steering in two directions from mode b to mode \(a_2\) and from mode \(a_2\) to mode b in the absence of the NDPA. Using the logarithmic negativity \(E_N\), we numerically show that the maximum value of optomechanical entanglement between modes b and \(a_2\) is around 0.4 achieved. The values of Gaussian steering \(\mathcal {G}^{b\rightarrow a_2}\) and \(\mathcal {G}^{a_2\rightarrow b}\) close to 0.02 and 0.1, respectively. In Fig. 2b, we consider non-resonant coupling between two optical modes (i.e., \(\lambda =0.2\omega _m\)) to show the influence of the NDPA on optomechanical entanglement and Gaussian steering between modes b and \(a_2\). Compared with Fig. 2a, it can be clearly observed that optomechanical entanglement and Gaussian steering can be effectively enhanced, in which the maximum optomechanical entanglement can reach 1.3, and Gaussian steering \(\mathcal {G}^{b\rightarrow a_2}\) (\(\mathcal {G}^{a_2\rightarrow b}\)) can reach 0.5 (0.6). In addition, the maximum values of optomechanical entanglement and Gaussian steering are around \(G=0.3\omega _m\) due to the influence of the non-resonant coupling between two optical modes.
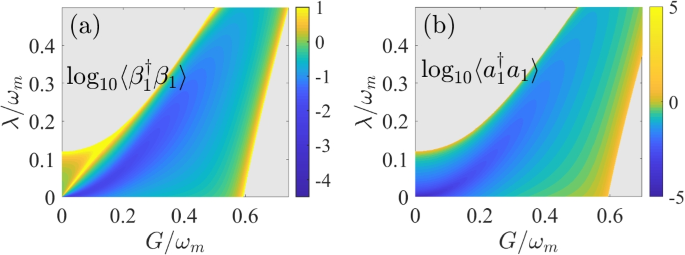
The steady-state population number of a the Bogoliubov mode \(\langle \beta _1^\dagger \beta _1\rangle\) and b the steady-state population number of the photon mode \(\langle a_1^\dagger a_1\rangle\) versus the optomechanical coupling strength G and gain \(\lambda\) for \(J=0.5\omega _m\). The other parameters are the same as Fig. 2
To further analyze the effects of NDPA on the optomechanical entanglement and Guassian streeing between the mechanical mode b and the optical mode \(a_2\), we introduce the delocalized Bogoliubov modes \(\beta _1=\delta b\text {cosh}r+\delta a_2^\dagger \text {sinh}r\) and \(\beta _2=\delta a_2\text {cosh}r+\delta b^\dagger \text {sinh}r\). Therefore, we can eliminate the parametric-down-converted-type interaction term between the optical mode \(a_1\) and the delocalized Bogoliubov mode \(\beta _2\) when \(r=\text {arctan}(\lambda /G)\). According to the delocalized Bogoliubov modes \(\beta _1\) and \(\beta _2\), the full linearized Hamiltonian of Eq. (5) can be rewritten as
Here, there is the resonant beam-splitter-type interaction instead of the parametric-down-converted-type interaction between optical mode \(a_1\) and Bogoliubov mode \(\beta _2\). Therefore, it can be easily discovered that the coherent population transfer from Bogoliubov mode \(\beta _2\) to optical mode \(a_1\) can cause ground-state cooling of Bogoliubov mode \(\beta _2\). Moreover, there are both the beam-splitter-type interaction \(a_1^\dagger \beta _1\) with strength \(\sqrt{G^2-\lambda ^2}\) and the parametric-down-converted-type interaction \(a_1^\dagger \beta _1^\dagger\) with strength \(\sqrt{G^2-\lambda ^2}-(J-\lambda )\text {sinh}r\) between the optical mode \(a_1\) and the Bogoliubov mode \(\beta _1\). The Bogoliubov mode \(\beta _2\) can be decoupled from optical mode \(a_1\) when \(J=\lambda\). In this case, the resonant beam-splitter-type interaction and the parametric-down-converted-type interaction has the same coupling strength \(\sqrt{G^2-\lambda ^2}\) between optical mode \(a_1\) and Bogoliubov mode \(\beta _1\). In the case of \(J<\lambda\), the strength of the parametric-down-converted-type interaction between optical mode \(a_1\) and Bogoliubov mode \(\beta _1\) is increased. As a consequence, the enhanced heating process is significantly stronger than the cooling process, which results in the increase for the population of modes \(\beta _1\) and \(a_1\). Moreover, the stability of the system can be satisfied if \(\sqrt{G^2-\lambda ^2}-(J-\lambda )\text {sinh}r\ll \omega _m\). For \(J>\lambda\), the strength of the parametric-down-converted-type interaction between optical mode \(a_1\) and Bogoliubov mode \(\beta _1\) can be effectively suppressed. In particular, the parametric-down-converted-type interaction strength is zero with \(J=G^2/\lambda\), while the heating process can be significantly suppressed between Bogoliubov mode \(\beta _1\) and optical mode \(a_1\).
In Fig. 3, we plot the populations of the Bogoliubov mode \(\beta _1\) and optical mode \(a_1\) for fixed tunneling interaction strength J. As plotted in Fig. 3a, we show the steady-state population number of the Bogoliubov mode \(\beta _1\) as a function of the effective optomechanical interaction strength \(G/\omega _m\) and the gain of NDPA \(\lambda /\omega _m\). It is worth noting that Bogoliubov mode \(\beta _1\) cannot be effectively cooled at the boundary between stability and instability regions, owing to a significantly large value of its steady-state population number. Furthermore, the steady-state average population number of mode \(\beta _1\) is still very high at \(G=\lambda\), which is due to the cooling process is effectively suppressed while the heating process still exists between the optical mode \(a_1\) and the Bogoliubov mode \(\beta _1\). In Fig. 3b, we show the steady-state mean photon number of optical mode \(a_1\). It is seen that the steady-state mean photon number of optical mode \(a_1\) can be well cooled within the blue region. This is due to the heating process between the two modes is suppressed (i.e., \(\sqrt{G^2-\lambda ^2}-(J-\lambda )\text {sinh}r=0\)) while the cooling process still exists (i.e., \(\sqrt{G^2-\lambda ^2}\ne 0\)) in the case of \(\lambda =G^2/J\).
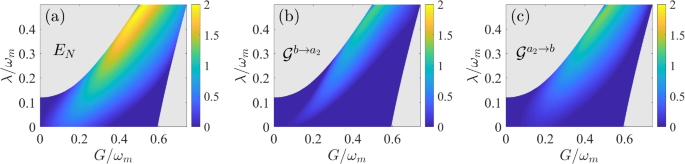
a Steady-state optomechanical entanglement \(E_N\), b Gaussian steering \(\mathcal {G}^{b\rightarrow a_2}\), and c \(\mathcal {G}^{a_2\rightarrow b}\) versus the optomechanical coupling strength G and gain \(\lambda\) for \(J=0.5\omega _m\). The other parameters are the same as Fig. 2
In Fig. 4a, we show the steady-state optomechanical entanglement \(E_N\) between the optical mode \(a_2\) and the mechanical mode b as a function of the effective optomechanical interaction strength \(G/\omega _m\) and the gain of NDPA \(\lambda /\omega _m\) with \(J=0.5\omega _m\). It can be obviously observed that the optomechanical entanglement can be significantly enhanced with the presence of NDPA. Moreover, optomechanical entanglement with maximum value appears near \(\lambda =G^2/J\). This is because under the condition, the heating process between Bogoliubov mode \(\beta _1\) and optical mode \(a_1\) is suppressed, while the cooling process is retained. We also find that the optomechanical entanglement is almost not existent at \(G=\lambda\), which is because the cooling process between the Bogoliubov mode \(\beta _1\) and the optical mode \(a_1\) is completely suppressed under this parameter regime, while the heating process is retained. Therefore, the steady-state population number of the Bogoliubov mode \(\beta _1\) is increased, which obviously inhibits the appearance of optomechanical entanglement. As is well known, the enhancement of the steady-state optomechanical entanglement results in the stronger Guassian steering between the optical mode \(a_2\) and the mechanical mode b. As shown in Fig. 4b, c, we show the Gaussian steering \(\mathcal {G}^{b\rightarrow a_2}\) and \(\mathcal {G}^{a_2\rightarrow b}\) as a function of the effective optomechanical interaction strength \(G/\omega _m\) and the gain of NDPA \(\lambda /\omega _m\) with \(J=0.5\omega _m\). The maximum Gaussian steering is consistent with the maximum optomechanical entanglement at \(\lambda =G^2/J\). With the presence of NDPA gain, the maximum Gaussian steering values \(\mathcal {G}^{b\rightarrow a_2}\) and \(\mathcal {G}^{a_2\rightarrow b}\) can be increased to 1.2 and 1.3, respectively. In addition, the Gaussian steering \(\mathcal {G}^{a_2\rightarrow b}\) is slightly stronger than \(\mathcal {G}^{b\rightarrow a_2}\) under the above mentioned parameter regime.
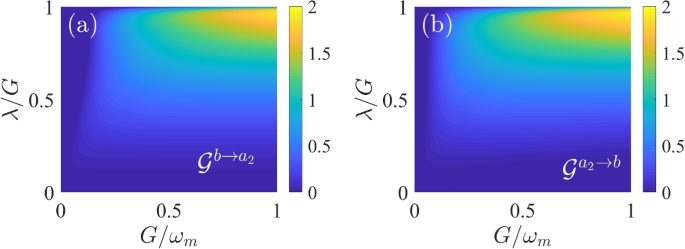
The steady-state Gaussian steering a \(\mathcal {G}^{b\rightarrow a_2}\) and b \(\mathcal {G}^{a_2\rightarrow b}\) versus the optomechanical coupling strength G and gain \(\lambda /G\) for \(J=G^2/\lambda\). The other parameters are the same as Fig. 2
To further investigate the optimal Gaussian steering between the optical mode \(a_2\) and the mechanical mode b in the stable region, we respectively show the Gaussian steering \(\mathcal {G}^{b\rightarrow a_2}\) and \(\mathcal {G}^{a_2\rightarrow b}\) as a function of the effective optomechanical interaction strength \(G/\omega _m\) and the ratio of the NDPA gain and the effective optomechanical interaction strength \(\lambda /G\) with \(J=G^2/\lambda\), as plotted in Fig. 5a, b. For the fixed effective optomechanical interaction strength, the steady-state Gaussian steering \(\mathcal {G}^{b\rightarrow a_2}\) and \(\mathcal {G}^{a_2\rightarrow b}\) are also significantly enhanced as the ratio of NDPA gain to the effective optomechanical coupling strength increases when \(\lambda /G<1\). However, the Gaussian steering \(\mathcal {G}^{b\rightarrow a_2}\) and \(\mathcal {G}^{a_2\rightarrow b}\) vanish rapidly near \(\lambda /G=1\) due to the suppression of the cooling process between the Bogoliubov mode \(\beta _1\) and the optical mode \(a_1\) and the retention of the heating process. The increase of the steady-state average occupancy of the Bogoliubov mode \(\beta _1\) leads to the destruction of Gaussian steering between the optical mode \(a_2\) and the mechanical mode b. In addition, for a fixed ratio \(\lambda /G\), the steady-state Gaussian steering between the optical mode \(a_2\) and the mechanical mode b can be increased with the increase of the effective optomechanical coupling strength G. The increased NDPA gain \(\lambda\) can effectively cause the enhancement of the steady-state optomechanical entanglement \(E_N\) and the Gaussian steering \(\mathcal {G}^{b\rightarrow a_2}\) and \(\mathcal {G}^{a_2\rightarrow b}\).
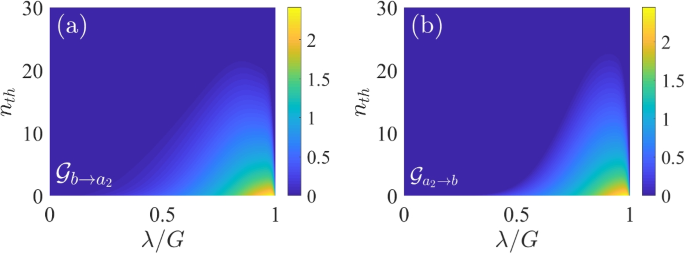
The steady-state Gaussian steering a \(\mathcal {G}^{b\rightarrow a_2}\) and b \(\mathcal {G}^{a_2\rightarrow b}\) versus the mean thermal phonon number \(n_{th}\). We set \(G=2\omega _m\), \(J=G^2/\lambda\), and the other parameters are the same as Fig. 2
Next, we investigate the robustness of the Gaussian steering between the mechanical mode b and the optical mode \(a_2\) to the environmental thermal noise. In Fig. 6, we can easily observe that the gain of the NDPA not only effectively increases the strength of the Gaussian steering, but also improves the robustness of the Gaussian steering to the environmental temperature. However, it is worth noting that the mean population number of the delocalized Bogoliubov mode \(\beta _1\) is significantly enhanced. Then, there is no Gaussian steering between the mechanical mode b and the optical mode \(a_2\) in the case of \(\lambda /G\rightarrow 1\).
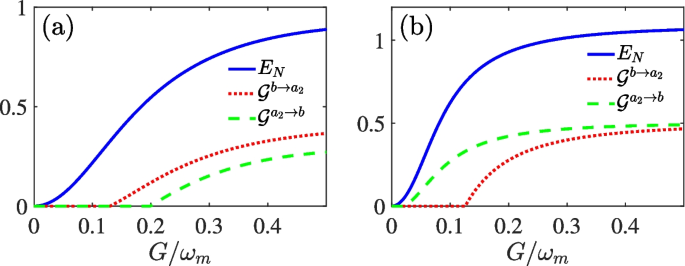
The steady-state optomechanical entanglement \(E_N\) and Gaussian steering \(\mathcal {G}^{b\rightarrow a_2}\) and \(\mathcal {G}^{a_2\rightarrow b}\) versus the optomechanical coupling strength G for a \(\kappa _2=0.1\omega _m\) and b \(\kappa _2=0.001\omega _m\). We set \(\lambda =0.5G\), \(J=G^2/\lambda\), and the other parameters are same as Fig. 2
In the previous discussion, due to the asymmetric coupling among subsystems, we find that the Gaussian steering \(\mathcal {G}^{a_2\rightarrow b}\) is always greater than \(\mathcal {G}^{b\rightarrow a_2}\). To further investigate the magnitudes of Gaussian steering \(\mathcal {G}^{b\rightarrow a_2}\) and \(\mathcal {G}^{a_2\rightarrow b}\), we analyze the influence of optomechanical interaction \(G/\omega _m\) on the Gaussian steering for the different loss rates \(\kappa _2\), as shown in Fig. 7a, b. We still choose the tunneling coupling strength \(J=G^2/\lambda\) to show the optimal steady-state optomechanical entanglement. Setting the NDPA gain \(\lambda = 0.5G\), the increased NDPA gain can effectively enhance the Gaussian steering from the mechanical mode b to the optical mode \(a_2\) with the increase of the effective optomechanical interaction strength G. When \(\kappa _2=0.1\omega _m\), the value of the steering \(\mathcal {G}^{b\rightarrow a_2}\) is larger than \(\mathcal {G}^{a_2\rightarrow b}\), which means that the Gaussian steerability from b to \(a_2\) is stronger than from \(a_2\) to b. While the case of the steering parameter \(\mathcal {G}^{a_2\rightarrow b}\) that is stronger than \(\mathcal {G}^{a_2\rightarrow b}\) can be realized for \(\kappa _2=0.001\omega _m\). Therefore, the asymmetric and one-way steering in the system can be obtained by adjusting the damping rate \(\kappa _2\) and the strength of the optomechanical coupling G.
Conclusion
We have studied the optomechanical entanglement and Gaussian steering in a three-mode cavity optomechanical system consisting of two optical cavities and a mechanical oscillator. There are the weak asymmetric Gaussian steering between the auxiliary optical mode and the mechanical mode, which is induced by the Stokes transition process in the optomechanical interaction. Owing to the existence of NDPA, not only the beam-splitter-type tunneling interaction exists between the two optical cavities, but also the parametric-down-converted-type interaction exists between them. Therefore, the optomechanical entanglement and the Gaussian steering in the system can be significantly enhanced. By inhibiting the heating process between the delocalized mode and the optical mode, we can easily observe the optimal optomechanical entanglement and Gaussian steering between two modes without direct interaction. Furthermore, the magnitude of the Gaussian steering in two different directions can also be adjusted by the dissipation rate of the cavity mode. Our proposal provides an effective method to manipulate and enhance the one-way Gaussian steering between the two modes.