Introduction
Over the last thirty or so years, there has been a huge amount of research being done in the field of quantum computers. In the last few years, a short survey by the authors records that the ArXiv on average receives around a dozen quantum computing-related submissions each day. What underpins all this interest is the promise of quantum computers, with its potential ability to solve incredibly hard, yet practical, problems that are unfeasible or intractable on any classical computer. Needless to say, many government and industrial organizations have shown tremendous interest in the area. Like the rise of classical computing machines, nobody would like to be left behind in the growing technology.
However, quantum computers are still far from achieving all that they have promised. While early-stage quantum computers have been developed, the problems of noisy calculations and scalability of quantum computers still plague the field. As opposed to the far future, where quantum computers can be as big as we wish them to be and are capable of performing fully controllable operations (termed as the fault-tolerant era), we are currently working in the Noisy Intermediate-Scale Quantum (NISQ) era, which is an operational definition that implies that the quantum computers available to us now are subject to substantial error rates and they are constrained in size (in terms of the number of qubits). While it is already a scientific achievement to get to this stage, such quantum computers are still incapable of showing any significant advantages over classical computers.
As such, some people in the community have already expressed fear that there will be a ‘Quantum winter’, or a scenario where quantum computing devices remain noisy and are unable to scale up in terms of qubit size, preventing us from ever achieving a meaningful advantage over classical computers. Under such an environment, funding and enthusiasm for quantum computing devices will dry up, leaving the field in a state of stagnation, with little or negligible resources, and hence, the field will spiral into a vicious cycle of little or no advances. Businesses in the field will also be unable to break out into profitable industrial applications and they are confined to niche research applications. Career paths of the many quantum scientists then wither and face uncertainty and extinction.
To prevent this from happening, we believe that it is important to set the achievements of the field in context. There have been some very significant achievements, and there is constant progress in the development of the field, but we are still far from realizing any sort of useful quantum advantage over classical computers. We do expect that we will eventually get there, but it is far too hard to divine when this will happen. By writing this review, we hope to illumine scientifically literate people who are outside the quantum computing field on a broad outline of the state of the art in the field. We also hope to provide some thoughts to some of these questions:
-
Where are we in the development of quantum computers, relative to the timeline of how classical computers were developed?
-
What are the most promising candidate platforms to physically implement the future quantum computers? And what are the pros and drawbacks of these platforms?
-
What are the most immediate problems that quantum computers can be applied to? What are the ‘killer apps’? What are the most immediate outcomes?
-
How can the cost of researching and developing quantum computers be justified in the short to medium term?
Brief history of classical computing
Living in the information era, where cheap classical computers with plenty of computing power are freely available, and in an era in which we rely on some form of computer (or even a mobile phone) for many daily tasks, we easily take for granted the development of the classical computer. To give some context on exactly how long it took us to get to this point, we briefly run through a short history of classical computing.
Computing devices can be traced all the way back to invention of the abacus in Sumeria. The abacus then evolved into the calculating machines like the Pascaline (young Pascal’s invention of a calculator to solve his father’s as a tax supervisor) and Liebniz’s Step Reckoner. Liebniz is also largely responsible for the development of the binary number system which now lies at the heart of modern computing. Yet, modern computers as we know today probably have a much shorter history.
In the early nineteenth century, Joseph Jacquard created a punch-card programmable loom to simplify the weaving process, though he had no intentions of using his work for computing. The first step towards a modern computer was probably due to the ideas and proposals by Charles Babbage around 1837. Although Babbage’s analytical machine was never actually built, its design embodied major features of modern computers: the input units, the memory, the central processing unit and the output units. Around the 1840s, Ada Lovelace became fascinated with Babbage’s analytical engine and she developed the first computer algorithm to compute Bernoulli numbers. Around the same time period, mechanical devices which would later be known as ‘differential analyzers’ were being designed to integrate differential equations. The first widely used differential analyzer was constructed in 1930s, and in the early 1940s, these differential analyzers were used in the computation of artillery firing tables prior to the invention of the ENIAC. In 1941, Claude Shannon introduced the idea of a General Purpose Analog Computer (GPAC).
At the turn of the twentieth century, Herman Hollerith created a tabulating machine to help calculate the US census with punch cards based on Jacquard’s loom. In 1936, Alan Turing published the idea of the Turing Machine. Also in 1936, Alonzo Church invented the λ-calculus, which is a formalization of how to express computations in mathematical logic. Prior to 1936, broadly speaking, people had an intuitive yet informal understanding of algorithms and computation. The work of Turing and Church helped to provide a mathematically rigorous framework for thinking about algorithms and computation, as stated in the famous Church-Turing thesis, one version of which is taken from [1]: ‘The class of functions computable by a Turing machine corresponds exactly to the class of functions which we would naturally regard as being computable by an algorithm’. From the Church-Turing thesis, we also get the notion of Turing Completeness: a computational system that can compute every function that a Turing machine can is Turing-complete. Using this framework, we can classify things like the abacus and the Pascaline, which can only solve a few specific problems, e.g. arithmetic, as devices that are not Turing complete. On the other hand, Babbage’s analytical engine would have been the first Turing-complete machine if it had been built, and hence, it could have been said to be the first programmable computer. Recently, it has also been shown [2] that Shannon’s General Purpose Analog Computer (GPAC) is equivalent to a Turing machine, and, as the name indicates, it operates in an analog fashion.
Further theoretical work on classical computation gave birth to the field of computational complexity, which is roughly stated as the analysis of the difficultly of solving computational problems, where the difficulty of a computational problem is quantified by the amount of time and space required by algorithms that solve the computational problem. Computational problems can then be classified into different complexity classes based on the difficulty of the problem. Two important examples are the complexity classes P and NP. Denoting the input size of a computational problem by n, the problem is said to be in the complexity class P if the time requirement of the algorithm that solves the problem scales polynomially with n. A problem is also said to be in the complexity class NP if we can verify proposed solutions to a problem in a time that scales polynomially with n. Clearly, P⊂NP, since being able to solve a problem in polynomial time would imply an ability to verify proposed solutions in polynomial time. However, it still remains an open problem whether P=NP.
It took the outbreak of World War II, and an immediate, pressing problem, to give birth to the first electronic, programmable computer. To crack German army communication codes, the Colossus was built in the UK in 1943, which was built with vacuum tubes, and the machine was able to be configured to perform a large variety of boolean logical operations. It however was not Turing complete. A similar computer, ENIAC, was built in the USA soon after. While the machine was huge, immensely power hungry and incredibly slow compared to modern devices, its improvements over the Colossus made it Turing complete, earning it the right to be called the first universal (programmable) classical computer.
Even then, the use of computers required further scientific advances to become widespread. Infamously, Thomas Watson, the president of IBM in 1943, predicted that there would only be a market for five computers in the world. With the benefit of hindsight, his prediction might seem somewhat foolish to us today. Yet, in his time, many people did not fully appreciate all the capabilities and potential of computers. People were not used to solving problems with the help of computers, and it was not known how to use computers outside of specific use cases, like the aforementioned cracking of German codes. It took the development of the Integrated Circuit in the 1950s and the Microprocessor in the 1960s before computers started to become commonplace in industries and academia. Since its development, the use of computers has become widespread, as a positive feedback loop developed: as more and more industrial and academic researches were done on computers, more algorithms and use cases for computers were concomitantly discovered. This has in turn spurred further improvements in the physical components of computers (famously described by Moore’s Law, which predicted that computing power would double every two years). With more powerful computers, researchers had greater access to computing power, which allowed them to continue proposing new applications for computers. The rest, as they say, is history.
Introduction to quantum computers
Quantum computers, by comparison, have a much shorter history. It probably starts in the late seventies or eighties as a science fiction topic. However, it enjoys (suffers?) far more hype in popular media.
Richard Feynman is universally acknowledged as the first proponent of developing a quantum computer [3]. In 1981, Feynman spoke at a conference, where he proposed the idea of using a quantum computer to simulate quantum systems that are too hard to simulate on classical digital computers [4]. The difficulty of classically simulating quantum systems arises from the fact that a system’s Hilbert space dimension scales exponentially with the system size. Most famously, he summarized the problem in this manner: ‘Nature isn’t classical, dammit, and if you want to make a simulation of Nature, you’d better make it quantum mechanical’. He was not the only one with such ideas. In 1980, the mathematician Yuri Manin [5] was also thinking of the exponential cost in memory and processing power that simulating a quantum many-particle system would require on a classical computer. The physicist Paul Benioff [6] was also wondering if it was possible to construct a quantum mechanical Hamiltonian model of computation. In 1985, Deutsch described the idea of a quantum generalization to a class of Turing machines, formalizing the idea of a universal quantum computer. He also suggested that such devices might be endowed with properties that are not reproducible by any classical computer [7]. At this point, it is helpful to distinguish between quantum simulators which are designed solely to solve a specific type of problem, and programmable quantum devices which are the quantum generalizations of the Turing machines described above.
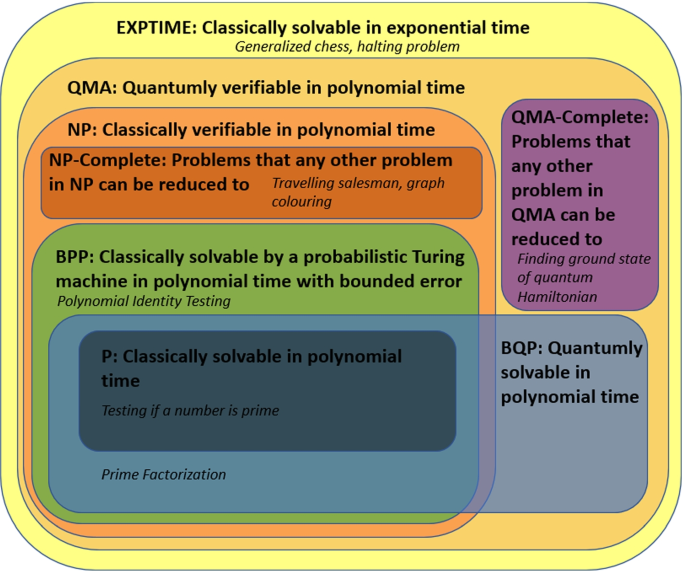
Several years later, the first quantum algorithms were developed that promised to solve certain contrived problems more efficiently than the best known classical algorithms [8, 9]. It was then shown that there was a separation between the class of problems solved by quantum computers in polynomial time and the class of problems solved by probabilistic classical Turing machines in polynomial time, suggesting that it was indeed possible to obtain quantum supremacy, or in other words, the ability of quantum computers to perform computations that are impossible or extremely hard for classical computers [10]. Not long after, Simon proposed an algorithm for quantum computers that could achieve exponential speedups in solving an idealized version of the problem of finding the period of a function [11], and this led Shor to develop an algorithm to efficiently prime factorize large numbers [12]. This problem had obvious applications in modern cryptography, being able potentially to crack the widely used Rivest-Shamir-Adleman (RSA) encryption that has been pervasively applied to many banking systems. Shor’s algorithm thereafter sparked much interest in quantum computing. Soon after, Grover proposed a quantum search algorithm for an unstructured database that had a mathematically provable quadratic speedup over the best classical algorithm [13]. This quadratic speedup suggests that while quantum computers will not be able to reduce all problems from exponential time to polynomial time, it is still interesting to reduce the polynomial complexity in certain problems and attain substantial speedups. During this time, Seth Lloyd also proposed an algorithm (colloquially known as Trotterization) for simulating other arbitrary quantum systems [14] on a quantum computer, which promised to accomplish the task originally proposed by Feynman of ‘making a simulation of Nature’. A diagram illustrating how quantum computers could provide advantages, in the language of computational complexity classes, is shown in Fig. 1.
Diagram illustrates how some relevant complexity classes, along with problem examples, relate to each other. The containment relations are only suggestive, with some of the relations still unknown. For example, it is still not known how the Bounded-error Probabilistic Polynomial time class (BPP) relates to the other classes, although it is suspected that it is a subset of NP. Another example would be the famous open question if P = NP. The two most important complexity classes to help us understand the potential power of quantum classes are Quantum Merlin Arthur (QMA) and Bounded-error Quantum Polynomial time (BQP). BQP can be understood as a quantum analog of the classical Bounded-error Probabilistic Polynomial time (BPP) class, which the P class is believed to be a subset of, that represents problems that can be solved efficiently on a quantum computer. Similarly, QMA can be understood as the quantum analog of NP, which represents problems that cannot be solved, but of which solutions can be checked efficiently, on a quantum computer. The precise locations where BQP is located in the hierarchy of complexity classes is still not known. It is hoped that there exist problems that are not in P, but in BQP, of which prime factorization is believed to be one. Such problems are prime candidates to demonstrate the superiority of quantum computers to classical ones. Figure heavily references [15]
In the case of classical computing, while the Turing machine model of computation is conceptually very useful, there are other equivalent models of computation such as the circuit model of computation. Two models of computation are said to be equivalent if the class of functions that can be computed on both models are the same. Similarly in the case of quantum computing, there are a few equivalent models of quantum computation to understand quantum algorithms and quantum computers. For example, the quantum Turing machine model of computation mentioned above is equivalent to the quantum circuit model of computation [16]. This is equivalent to an alternative model which is somewhat less popular, called the adiabatic quantum computing model of computation [17], which is built on the idea of achieving a quantum computation by utilizing the adiabatic theorem in quantum mechanics. By slowly evolving a quantum ground state from a known Hamiltonian to a complicated Hamiltonian, we are able to solve any problem that a quantum computer built on the quantum circuit model is capable of solving. In this work, while we will describe most of the algorithms using the quantum circuit model, we want to emphasize that is not the only way to do so Footnote 1. All algorithms described above, like the Grover search algorithm, can be described both with a quantum circuit model of computation and also with a adiabatic quantum computing model of computation [19].
Why NISQ?
Right from the very start, there have been skeptics that challenged the possibility of a quantum computer superseding the power of a classical Turing machine. Most of these arguments are founded on beliefs that such quantum computation devices would be exponentially hard and complex to control [20,21,22,23,24]. The effect of decoherence underlies all these arguments, which is the phenomenon of quantum systems interacting with the environment over time, causing it to lose its quantum behaviour. Based on the difficulty of controlling a quantum computer, there are arguments that claim that quantum computing will never be able to obtain quantum supremacy [25], or at the very least, have non-trivial conditions that must be satisfied in order to realize quantum supremacy [26].
While small scale demonstrations of algorithms such Shor’s algorithm, Grover’s algorithm, or Deutsch–Jozsa’s algorithm on early noisy quantum computers [27,28,29,30] have been performed, we know that it would be pointless to scale such algorithms up at this point in time, as the current error rates and noise inevitably destroy any precision in the results that we can obtain from these noisy quantum computers. The capability to control and protect our qubits in a quantum computer to the degree necessary to run such algorithms is commonly described as fault-tolerant quantum computation. To achieve full fault tolerance, we either need order of magnitude improvements in the control and stability of our physical qubits or need to rely on error-correcting codes. Classical error-correcting codes work by aiming to encode a single logical bit on multiple physical bits by employing redundancy. However, the quantum no-cloning theorem [31] prevents classical methods from being applied directly on quantum computers. Nevertheless, in the quantum case, it was first shown by Shor in 1995 that it is possible to encode the information on one logical qubit onto a highly entangled state of multiple physical qubits, protecting it against limited errors [32]. This process is otherwise known as Quantum Error Correction (QEC). It was also shown by Shor that such methods allow us to execute a quantum computation reliably with noisy hardware, or in other words, physical qubits subjected to decoherence and other errors [33].
Soon after it was understood that, in principle, if the errors and noise affecting the quantum computer are below a certain threshold, it is possible in principle to scale up quantum computers to large devices [34,35,36]. Since then, many other types of codes have been developed, and there has been much work in this field [37,38,39]. Unfortunately, estimates of the number of physical qubits needed for getting a useful amount of logical qubits with all currently proposed error-correcting codes are minimally in the range of millions [40]. Even if this is eventually possible, the current state of the field of quantum computing, with the state of the art devices maxing out at around a few hundred qubits, suggests that this will only come in the far future.
Regardless of this debate on fault tolerance, in recent years, there have been a few landmark experiments that claim that they have achieved quantum supremacy. They were able to carry out computations on a semi-programmable quantum computing device that we believe are not able to be computed on classical computing devices in any reasonable amount of time. One of the first experiments to make this claim was the Google AI Quantum team in 2019 [41] and was closely followed by the USTC team and their Jiuzhang photonic quantum computer in 2020 [42]. Pictures of the experimental setups are found in Fig. 2. These quantum computers are significant achievements in their own rights, with significant degrees of programmable capability and control. Yet we are still far away from being fault-tolerant, as these machines are only able to execute circuits of limited depth and they are subject to significant error and decoherence rates with low number of qubits (≈50 qubits). While progress has been made to increase the number of qubits, with IBM announcing recently that they have a quantum computer with 127 universal, controllable qubits [43], and Xanadu demonstrating significant achievements in scaling up photonic quantum computers [44], these machines are still far from the scale needed to execute error correcting codes.
In light of these developments, the term NISQ [45] computing was coined to refer to the current era of quantum computing. This is distinct from the holy grail of the field in the far future, termed the fault-tolerant era of quantum computing. We want to emphasize that NISQ is a hardware-focused working definition, and does not necessarily imply a temporal connotation. Noisy implies that such quantum computers are subject to large enough error and decoherence rates such that their computational powers are limited. Intermediate-Scale implies that while they are large enough such that they are probably not able to be simulated with brute force by classical computers, they are still not large enough to be error corrected, which also contributes to the previous point of them being noisy.
In the long term, we should view the NISQ era as a step towards full fault tolerance and the development of more powerful quantum devices. We do not expect NISQ devices to be fully capable of realising the power of quantum computers. Yet this does not prevent us from studying the power of existing quantum computers and making progress in the field. However, one should note that we may be in this era for a long time. As such, research in the NISQ era is important, as we do not know how long we will take to realize full fault tolerance, and in any case, NISQ technology is exciting, as it could provide us with new tools to explore problems such as highly complex many-body quantum systems that are not feasible to be simulated with our current technology. Furthermore, we still do not have that many quantum algorithms for the fault-tolerant era, which is probably a result of how the rules of quantum mechanics (and thus quantum computation) are not sufficiently intuitive for most people. We clearly need to take a page from the history of classical computers and learn from it. As classical computers improved, with more and more budding computer programmers entering the field of computer science, the field has developed incredibly fast. Programmers were quickly able to better understand the power of classical computers and how to construct algorithms for them. It is also only natural to expect that as NISQ devices are promulgated, and as more and more physicists and quantum computer scientists work on NISQ algorithms and devices, we should also expect a similar renaissance in the field of quantum computing. The work and knowledge we produce in the NISQ era will definitely provide the impetus towards the fault-tolerant era.
NISQ algorithms
NISQ algorithms refers to those algorithms that are designed with the constraints of NISQ computers in mind. Most importantly, they are designed to be implementable on NISQ devices in the near term, i.e. the next few years. This also implies that NISQ programmers aim to use as many qubits as it is physically implementable. Such algorithms also promise to be somewhat tolerant to computational noise through error mitigation, and make no explicit reference to the absence of QEC. Error mitigation is the process by which users aim to build in mitigation strategies in their algorithms to account for the effects of computational noise [46], while as mentioned above QEC is the process by which methods are developed to build in a certain form of redundancy in the computation by storing information over multiple qubits [32, 47]. Lastly, NISQ algorithms aim to utilize only shallow-depth quantum circuits (right now, around a few hundred gates in depth at maximum) and as few complicated operations (like multi-qubit controlled unitaries) as possible.
In this framework, neither the Shor nor the Grover algorithm fits into the category of NISQ algorithms. This is because they both rely on oracle black box functions/unitaries that need extremely long and complicated circuits for execution on a quantum computer [48]. Moreover, quantum advantage cannot be gained with just a few noisy qubits in these algorithms. Furthermore, these algorithms are not explicitly noise tolerant, as small noise and error rates dramatically change the results of such computations. Full scale Trotterization does not fit into the category of NISQ algorithms too, since time simulation to arbitrarily long times require arbitrarily deep depth quantum circuits.
We realize that this definition of a NISQ algorithm is extremely subjective. For example, many researchers will have differing views on what constitutes ‘near term’, and what is a ‘complicated’ operation. However, we note that this operational definition is empirically motivated by the current experimental work. Most NISQ algorithms are run on current hardware, and many of these algorithms are tested experimentally right now. This stands in contrast to most algorithms that require fault tolerance, which cannot be carried out on current quantum computers aside from trivial examples (such as applying Shor’s algorithm for finding prime factors for the number 15). Indeed, most of these algorithms explicitly state that they require a substantial degree of fault tolerance to work.
In this paper, we provide a short introduction on the various NISQ algorithms developed so far. However, this list is by no means exhaustive, and for more information, one should refer to the works of Bharti et al. [15] and Cerezo et al. [49].
Variational quantum algorithms
In 2014, Peruzzo et al. [50] proposed the first variational quantum algorithm. The algorithm is now commonly known as Variational Quantum Eigensolver (VQE). That work contains all the essential concepts and tools for the whole range of VQAs, so we will describe that algorithm and its components in more detail.
Firstly, all VQAs require an objective function \(\mathcal {O}\). This objective function has the problem encoded within it. In the case of VQE, the problem is to find the ground state of a Hamiltonian H.
Secondly, all VQAs require a parameterized quantum circuit (PQC) that takes in a set of parameters θ. This PQC is generated by means of a parameterized unitary operation and is also typically known as the ansatz. This nomenclature makes a lot of sense if we define the state after application of the PQC as |Φ(θ)〉=U(θ)|Φ0〉, where θ are the variational parameters that contribute to the parameterized unitary operation and |Φ0〉 is some initial state that can be efficiently prepared on the quantum computer. Typically, this is the ground state of qubits, where all qubits are in |0〉. In the case of VQE, this means that we now can express the objective function as \(\mathcal {O}(\boldsymbol {\theta })=\langle \Phi _{0} | U^{\dagger }(\boldsymbol {\theta }) H U(\boldsymbol {\theta }) | \Phi _{0}\rangle\).
Thirdly, all VQAs need a way to measure \(\mathcal {O}(\boldsymbol {\theta })\). This is usually done on a quantum computer. Typically, \(\mathcal {O}(\boldsymbol {\theta })\) is expressed on the quantum computer by decomposing it into elementary gates that can be executed on the device. In the VQE case, H is a real observable and thus \(\mathcal {O}(\boldsymbol {\theta })\) is fully real and can be measured by applying a unitary transformation on the quantum state to the diagonal basis of the observable (in this case H). It is especially easy to do so if the Hamiltonian can be written in the form of a linear combination of Pauli strings, which are just tensor products of Pauli operators. In this case, the unitary rotations are just Pauli rotations and measurements can be done in the computational basis. By obtaining the probabilities of measuring each basis state from the quantum computer, we can then compute the value of \(\mathcal {O}(\boldsymbol {\theta })\).
Lastly, the VQA relies on an classical optimizer that runs on a classical computer, to minimize the objective function. In the VQE case, our problem is to find \(\min _{\boldsymbol {\theta }}\mathcal {O}(\boldsymbol {\theta })\), which corresponds to finding minθ〈Φ0|U†(θ)HU(θ)|Φ0〉. This sets up a quantum-classical feedback loop. Thus, the whole process of running VQE, and by extension, most VQAs, can be succinctly summarized as:
-
Encode the problem in an objective function.
-
Choose a PQC/ansatz.
-
Optimize the objective function over the parameter space of the PQC/ansatz by relying on a classical optimizer and a quantum computer to measure the value of the objective function in a quantum-classical feedback loop.
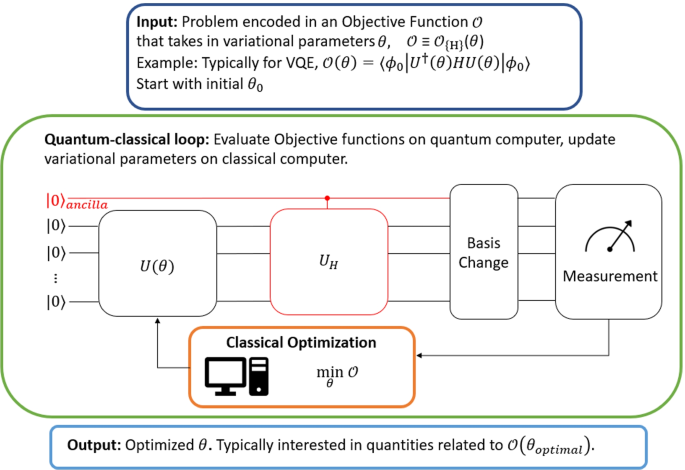
A diagram of the major steps in a VQA is shown in Fig. 3. VQAs are the most explored NISQ algorithms developed to date. However, VQAs contain significant problems that must be dealt with before it can achieve quantum supremacy, if it is even capable of doing so. Most of these problems are not unique to VQAs; however due to the simplicity of the structure of VQAs, it is usually easiest to understand these problems from the perspective of VQAs.
Figure adapted from [15]. Diagrammatic representation of a typical VQA. In the input stage, we encode the problem in an objective function, and next choose a PQC/ansatz. The circuits are then measured. This is typically achieved with basis changes or the help of Hadamard tests (labelled in red in the diagram), depending on the objective function. A classical optimizer is used to update the parameters. This gives rise to the quantum-classical feedback loop. At the end, after the optimizer has found the optimal parameters to minimize the objective function, we read out the result to gain the desired output
Firstly, it is now known that the expectation value of the gradient of the objective function corresponding to randomly initialized PQCs (RPQC) decays exponentially to zero as a function of the number of qubits [51,52,53]. This causes the training landscape to exponentially flatten as the number of qubits increases, making it exponentially hard to train. This issue is commonly called the barren plateau problem. Even gradient-free optimization routines are afflicted with this problem [54]. This problem is further compounded by the noise and errors in NISQ quantum computers [55]. It has been argued that the barren plateaus have their roots in the volume-law growth of entanglement in quantum systems [56] and that there are fundamental tradeoffs that have to be made between the ansatz expressibility and the trainability [57], and these works indicate that it is usually hard to discuss this problem without also discussing the expressibility problem of the ansatz (see later discussion). There have been many proposals to circumvent this problem focusing mainly on changing the ansatz structure [58,59,60], or changing the encoding of the problem [61, 62], or devising schemes to obtain good parameters [63, 64] or training the PQC layer by layer [65, 66]. Yet, it remains unclear if these methods can indeed overcome the barren plateau problem in NISQ devices. These methods can also impose additional constraints, for example the proposed PQCs/ansatz that are supposed to avoid the barren plateau are usually not hardware efficient in circuit design and hard to implement on a NISQ computer. Some alternative methods that are proposed to avoid the barren plateau, for example, by utilizing classical shadows [67], exist but we still need further study to determine if such techniques really provide a solution.
Secondly, the choice of PQC/ansatz is not always clear. The optimal PQC that we choose should be both trainable (discussed above) and expressible. Expressibility concerns whether the PQC is able to reach/access most parts of the Hilbert space and thus whether it is able to generate a rich class of quantum states. The number of PQC layers, parameters or entangling gates required to achieve a given accuracy is also linked to the expressibility of the circuit. Unfortunately, studies have shown that, typically, the more expressible we make our PQC, the less trainable is the circuit [57], up to the point where we over parameterize the circuit. There is also no well-agreed measure of expressibility. One proposed way is to measure how distributions of the fidelity of randomly generated states using the PQC differ from a similar distribution generated with Haar-random states, along with usage of the Meyer-Wallach Q measure [68] to estimate how well and what classes of entangled states a particular PQC can generate [69]. Another proposed measure is the parameter dimension of the PQC, which calculates the number of redundant parameters a PQC possesses [60]. Ideas from classical Fisher Information have also been used to characterize expressibility [70]. Many classes of circuits have been investigated with both measures [59, 60, 69], and it has been shown that certain PQC structures are indeed more expressible than others.
Thirdly, for the measurement step, in the general case, this overlap could have both real and imaginary parts. If so, the measurement step will be slightly more involved, requiring Hadamard tests, which comes at the cost of more complicated circuits and an additional ancillary qubit requirement [71, 72]. However, this problem is usually not as serious as the previous two and can be overcome by using methods found in [73].
Many VQAs are variants of VQE that deals with the problem of finding the spectrum of a given Hamiltonian. While the problem of estimating the ground state and its energy of a Hamiltonian is not expected to be efficiently solvable on a quantum computer in general [74], there is hope that approximate solutions can be found quicker, and also for larger systems, compared to what is possible on classical computers. Some notable developments on VQE are (i) those that adaptively improve the ansatz [75, 76], (ii) those that reduce the amount of qubits needed [77], (iii) those that improve the evaluation of gradients [78], (iv) those that extend it to open systems [79] and (v) those that use it to find excited states [80,81,82], just to name a few examples.
VQAs for simulating Hamiltonian evolution have also been developed. The most notable example is the Variational Quantum Simulator (VQS) [83,84,85]. Other interesting VQAs that deal with Hamiltonian evolution include those that restrict the evolution to a subspace [86], those that rely on finding approximate projections of the action of the time evolution operator on an ansatz [87, 88] and those that find approximate diagonalization of the time evolution unitary [89,90,91].
Quantum annealing
Introduced as the quantum analogue of simulated annealing (SA) [92], quantum annealing (QA) [93,94,95] is a heuristic (no guarantees on quantum speedup) optimization algorithm that aims to solve complex optimization problems [96]. This is done by encoding the solution of the problem into the ground state of what is called the annealer Hamiltonian [97] which is usually the transverse field Ising Hamiltonian,
where \(\sigma ^{z}_{i}\) is the Pauli Z operator on the ith site of the Ising model. Many optimization problems like job scheduling and chain optimization problems, with diverse applications, can be mapped into the problem of finding the ground state of such a transverse field Ising Hamiltonian.
In many cases, modelling the optimization problem is equivalent to a transformation of the Ising problem into a quadratic unconstrained binary optimization (QUBO) [98]. The QUBO formulation is then converted into a logical graph where nodes represent the variables and edges represent the interaction between the variables. Such logical graph naturally lends itself in the hardware implementation of the problem with the hardware implementation happening via a map called minor embedding of the logical graph into the physical graph of the quantum processing unit (QPU).
Once the hardware mapping is complete and the system is initialized into the ground state of an easy-to-solve Hamiltonian, the annealing process begins. This process is best understood the mechanism of stimulated annealing. The idea behind SA is that by starting in an initial random state at high temperature, and by adiabatically cooling the system, we are able to find the final ground state. Thermal excitations will allow the system to escape from local minima and relaxations during the cooling process.
In contrast, QA optimization makes use of quantum fluctuations as induced by the energy-time uncertainty relation to reach the optimum state. It starts out with an initialization of the system in a Hamiltonian that consists of the transverse field Ising Hamiltonian that encodes the QUBO problem, plus a kinetic term,
where \(\mathcal {H}_{kin} = -\sum _{i} \sigma _{i}^{x}\). Γ(t) is initialized at a high value such that the kinetic term dominates, and the ground state of such a Hamiltonian is a universal superposition of all the possible classical configurations. By adiabatically decreasing Γ(t) under some cooling schedule to zero, the quantum system stays near its instantaneous ground state. The goal is that at the end of the ‘cooling process’, the system lies in the true ground state of the final Hamiltonian, allowing us to access information about the solution of the optimization problem encoded in the Hamiltonian. The solution is typically read out via spin measurements of the final configuration. The annealing-readout step is repeated several times to determine the distribution of the final configuration states.
In such a process, quantum tunneling takes the role of thermal fluctuations, in which the system is able to escape instantaneously the local minima and explore neighbouring state space. The quantum fluctuations are parameterized by Γ(t), which explains why the term is usually called the kinetic term, as it provides a visual interpretation of the term and reveals its role in the annealing process. At high Γ(t), the system experiences very strong quantum fluctuations, allowing it to access almost all states, and as it cools down to zero ‘temperature’, the quantum fluctuations eventually diminish and allow us to slowly hone in on the true ground state.
There has been reasonable evidence to show that while in theory, QA can obtain significant speedups versus SA and other classical methods [99], there are conditions that might not be possible on an physical quantum device [100]. A crucial parameter that governs the accuracy of this optimization is the time scale over which the entire optimization occurs. Long enough time scales guarantee convergence to the ground state solution but short time scales could lead to the system converging to an excited state; therefore, there is a fundamental trade-off between computing time and computational accuracy of the QA optimization process.
QA also has applications in random sampling where sampling from many low energy states of the annealer helps to characterize the energy landscape. QA is closely related to one of the universal models of quantum computing, i.e. adiabatic quantum computing [101]. Indeed, it was first proposed as a practical implementation of adiabatic quantum computation. However, the current state of the art QA processors, for example those manufactured by D-Wave systems consisting of ∼ 2000 superconducting flux qubits [102], can only implement a subset of protocols required for universal quantum computation. Thus, practical implementations of QA still leaves plenty of room for improvement. More technical details about QA can be found in [98, 103].
Quantum Approximate Optimization Algorithm
The Quantum Approximate Optimization Algorithm, or QAOA for short, was introduced [104] as a way to solve combinatorial optimization problems on a quantum computer. As explained in Combinatorial optimization section, all combinatorial optimization problems can be interpreted as problems of finding the eigenvector corresponding to the largest eigenvalue of a Hamiltonian that is diagonal in the computational basis. The QAOA algorithm can be regarded as a variational quantum algorithm where one uses an ansatz inspired by quantum annealing to maximize the expectation value of a Hamiltonian Hc that is diagonal in the computational basis. More specifically, the variational ansatz is written as
where \(H_{m} = \sum _{j=1}^{N} \sigma _{j}^{x}\) is identical to the kinetic term in quantum annealing. This term Hm is also known as the mixing Hamiltonian. Here, \(|+\rangle = \frac {1}{\sqrt {2}}(|0\rangle + |1\rangle)\), and β=(β1,…,βp),γ=(γ1,…,γp) are the variational parameters that are to be optimized to maximize the following objective function \(\mathcal {O} = \langle \psi (\boldsymbol {\beta },\boldsymbol {\gamma })|H_{c}|\psi (\boldsymbol {\beta },\boldsymbol {\gamma })\rangle\). Similar to quantum annealing, the idea is to consider the following time-dependent Hamiltonian
For large T, by starting in the lowest energy eigenstate of −Hm which is |+〉⊗n, the system ends up in the lowest energy eigenstate of −Hc as t→T. By identifying \(\phantom {\dot {i}\!}\left (e^{-iH_{c}\beta _{p}}e^{-iH_{m}\gamma _{p}}\right) \dots \left (e^{-iH_{c}\beta _{1}}e^{-iH_{m}\gamma _{1}}\right)\) as the Trotterization of H(t) above, we arrive at the QAOA ansatz. As mentioned in [104], larger values of p in the ansatz lead to better approximate solutions. The success of the QAOA algorithm is mathematically guaranteed as p→∞ since the Trotterization becomes exact in that case.
It can be easily seen that QAOA shares similarities with quantum annealing. They both rely on an additional term that does not commute with the problem Hamiltonian, and whose role is to allow for quantum fluctuations to explore nearby states. However, some key differences exist. Firstly, while the goal in quantum annealing is to retain the state in its instantaneous ground state at all times, and to eliminate slowly the kinetic/mixing Hamiltonian, in QAOA, we are actually trying to alternate time evolution frantically between the problem Hamiltonian and the kinetic/mixing Hamiltonian. Secondly, we have in theory an infinite number of steps and we can easily choose parameters so that we follow the quantum annealing path with QAOA (and also guarantee the success of the algorithm); in practice, we want to avoid this way of doing things. We typically aim to solve the problem with as few steps as possible. In short, the QAOA algorithm can be regarded as an optimized cooling schedule for quantum annealing.
It should be noted that since we are limited to shallow circuits in the NISQ era, we are constrained to small values of p and hence approximate solutions to these combinatorial problems. Even so, QAOA remains a promising candidate algorithm for quantum advantage in the NISQ era, since it has been proven (under some reasonable complexity theoretic assumptions) that classical computers are unable to reproduce the output probability distribution of the bit strings generated by p=1 QAOA [105]. The performance of QAOA in the NISQ era can also be improved by slightly modifying the QAOA algorithm to a variant known as adaptive QAOA [106, 107]. Apart from solving combinatorial problems, QAOA can also be generalized to a form where it can be used to perform universal quantum computation [108, 109].
Boson Sampling/Gaussian Boson Sampling
Right at the beginning, there were questions on whether it is possible to achieve quantum supremacy in quantum computers, and how might one achieve it quickest. In 2011, Aaronson and Arkhipov proposed Boson Sampling as a candidate to achieve this feat [110]. The algorithm is designed with the expressed intention of demonstrating quantum supremacy.
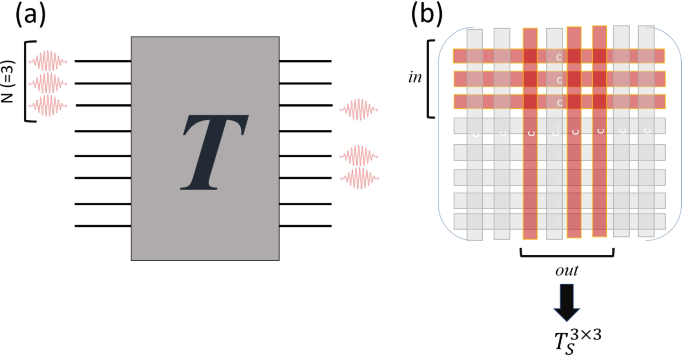
Boson Sampling considers the scenario of a Fock state of n photons entering an optical circuit of m modes. The optical circuit implements a series of phase shifters and beam splitters, with the phase shifters acting on a single mode j by adding a specified phase θ to that mode, \(R_{j}(\theta) = \exp {(i\theta a_{j}^{\dagger } a_{j})}\), and beam splitters acting on two modes j and k by modifying them in the manner \(\phantom {\dot {i}\!}B(\theta,\phi) = \exp {(\theta (e^{i\phi a_{j} a_{k}^{\dagger }}-e^{-i\phi a_{j}^{\dagger } a_{k}}))}\), where \(a_{j} (a_{j}^{\dagger })\) is the annihilation (creation) operator for the mode j. On a typical optical circuit with modes arranged in one-dimension, with sufficient phase shifters and beam splitters acting on adjacent modes, it is possible to implement an arbitrary m×m unitary matrix U on such a circuit [111,112,113] with post-selection. Aaronson and Arkhipov discovered that by sampling from the distribution of photons that passed through the optical circuit, the permanent of a related matrix could be efficiently calculated. As an illustration of how the algorithm works, we refer the reader to Fig. 4. Suppose we inject photons in the first three wave guides, denoted by the creation operators of the photons by \(a_{i}^{\dagger }\) (i=1...3) and study the probability of getting the photons at the third (\(b_{3}^{\dagger }\)), fifth (\(b_{5}^{\dagger }\)), and sixth (\(b_{6}^{\dagger }\)) outputs. The input and output ports are related to each other by the relation \(a_{i}^{\dagger } = \sum _{j} T_{ij} b_{j}^{\dagger }\). We see that
Figure adapted from [114]. An illustration of the Boson Sampling procedure. a N photons are injected into an interferometer T that simulates an unitary matrix. b By obtaining the probabilities of observing the output distribution of the photons n ̄, the permanent of a submatrix in T can be subsequently calculated, Pr(n ̄)=|Perm(Ts)|2
and by focusing on the term with \(b_{3}^{\dagger } b_{5}^{\dagger } b_{6}^{\dagger }\), then we see the probability of getting photons in output ports 3, 5 and 6 is proportional to
Interestingly, while calculating the determinant of a large matrix is tractable, thanks to Gaussian elimination, the permanent of a large matrix is computational hard. Indeed, there is no known efficient classical algorithm to accomplish such a task, and it is believed to be extremely unlikely due to the implications it would have on the polynomial hierarchy in computational complexity theory [115]. Consequently, a successful Boson Sampling experiment would be a demonstration of quantum supremacy.
However, the original Boson Sampling approach is difficult to scale up and implement experimentally. The biggest problem is the requirement of a reliable source of many indistinguishable photons. The most widely used method of generating single photons is Spontaneous Parametric Down-Conversion (SPDC) for many reasons, with two big reasons being its experimental simplicity and high photon indistinguishability. However, the SPDC process is probabilistic in nature, and this implies that if we would want to scale up the process and simultaneously produce a large amount of indistinguishable single photons, the probability of doing so would be exponentially rare, with it scaling as O(pN), where p is the probability of a SPDC process generating a single photon at a given time, and N the number of photons one would want to generate spontaneously.
To overcome these experimental limitations, Gaussian Boson Sampling (GBS) was proposed in 2017 [116]. This proposal was born out of the fact that experimentally, Gaussian input states, states of light whose Wigner quasi-probability distributions are of Gaussian shape, are much easier to produce and manipulate than pure single photon Fock states, and they can be created deterministically. This modifies the problem slightly; instead of sampling and calculating the permanent of a matrix in the original Boson Sampling case, we now solve a slightly different problem of sampling and calculating the Hafnian function of a matrix in the GBS case. The Hafnian is also in the complexity class #P, which means it is not believed to be solvable by a classical computer in polynomial time, implying that it is known to be a computationally hard problem. Solving the GBS would probably demonstrate a form of quantum supremacy. It was first experimentally demonstrated in 2019 [117] with up to 5 photons, and barely a year later, the same group demonstrated a GBS experiment on a scale that is believed to be not classically simulatable, possibly demonstrating quantum supremacy [42]. A detailed analysis on GBS can be found in [114].
While Boson Sampling/GBS has designed for the sole purpose of demonstrating quantum supremacy, with no expected practical applications, there have been proposals that suggest that it can be used for calculating molecular vibronic spectra in quantum chemistry [118,119,120], for sampling ground states of a classical Ising model [121] and for finding dense subgraphs [122].
As one might expect, the development of Boson Sampling and GBS is closely linked with the development of photonic quantum computing platforms. More details on the technology used can be found in our later section discussing photonics as a quantum computing platform. While the capability to perform Boson Sampling/GBS is not a form of universal quantum computing, it is typically seen as an experimental step towards realising universal quantum computing on photonics.
Quantum-assisted methods
Apart from VQAs mentioned above, another class of NISQ algorithms which we call quantum-assisted methods have been proposed [123,124,125,126,127]. These methods can be used for both finding the ground state energy of a given Hamiltonian and also for simulation of time evolution under a given Hamiltonian.
There are three main steps in this techniques. The first step is to first construct an ansatz state \(|\psi (\boldsymbol {\alpha })\rangle = \sum _{i} \alpha _{i} |\chi _{i}\rangle\) where the states |χi〉 are related to the Hamiltonian H of the problem. There are many possible ways to construct these problem-aware states |χi〉, but one particular choice of states that has been extensively used is the cummulative K moment states, first proposed in [123]. These cummulative K moment states are based on the idea of generating a Krylov subspace for the Hamiltonian H, which suitably encode the information about the problem information H. The next step is to construct the so-called D and E matrices by measuring on a quantum computer the matrix elements Dij=〈χi|H|χj〉 and Eij=〈χi|χj〉 respectively. For this step, there are certain simplifications that can be made based on the choice of states |χi〉 in the ansatz. For example, if the cummulative K moment states are used for the case where H is written as a linear combination of Pauli strings, then the measurement of the abovementioned matrix elements reduces to the problem of sampling an efficiently-preparable quantum state |ψ0〉 in different Pauli-rotated bases, which is easy to do on a NISQ computer. The last step is to do some classical post-processing with the D and E matrices on a classical computer. For the Hamiltonian ground state problem, the goal is to obtain the vector α∗ from the D and E matrices such that the ansatz state \(|\psi (\boldsymbol {\alpha ^{*}})\rangle = \sum _{i} \alpha _{i}^{*}|\chi _{i}\rangle\) corresponds to the lowest energy eigenstate. For the Hamiltonian simulation problem, the goal is to obtain the time-dependent vector α(t) from the D and E matrices such that the ansatz state \(|\psi (\boldsymbol {\alpha }(t))\rangle = \sum _{i} \alpha _{i}(t) |\chi _{i}\rangle\) corresponds to the state of the quantum system at time t.
From the above description, we see that similar to VQAs, the main idea is to use a classical computer together with a noisy quantum computer leveraging on the strengths of both types of computers. However, there are many important differences between the quantum-assisted methods and VQAs. Firstly, unlike VQAs, we see that the quantum-assisted methods do not rely on a feedback loop between a classical and a quantum computer, since all the required quantum computation is done in a single step. This is an advantage over VQAs, because the classical-quantum feedback loop can be a major bottleneck when running VQAs on cloud-based quantum computers, since each job for the quantum computer needs queuing and jobs have to be submitted to the quantum computer at each iteration of the feedback loop. Secondly, because the quantum assisted methods do not use a parametric quantum circuit, they avoid the barren plateau problem that typically plagues VQAs.
Hamiltonian evolution with Trotterization
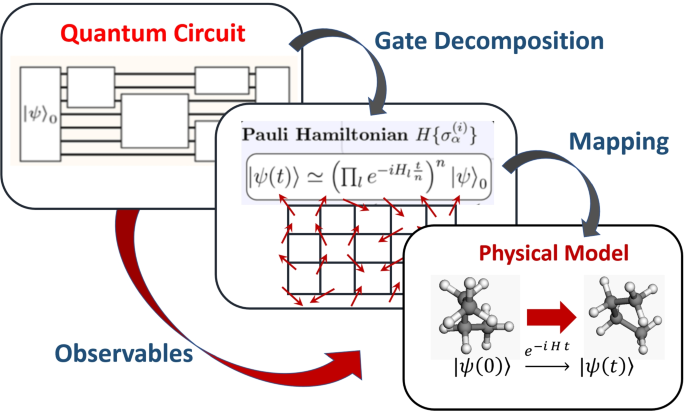
On classical computers, one method that is commonly used in simulating quantum dynamics is to utilize the Trotter-Suzuki [128, 129] decomposition of the unitary time evolution operator into small discrete steps. This allows us to approximately factorize the time evolution operator, avoiding the need to exactly diagonalize the Hamiltonian. The structure of such a method lends itself naturally to developing a similar method for simulating time-dynamics on quantum computers, and such a scheme is the idea behind the Trotterization algorithm mentioned above.
On a quantum computer, the evolution of a state under a Hamiltonian for long times is broken down into small steps. Each step is individually made up of efficiently implementable quantum gates, which can be run on the quantum computer. Due to its simplicity, there has been much theoretical analysis and experimental work on applying Trotterization on quantum computers [14, 130,131,132,133,134,135]. However, as mentioned previously, this method is currently thought to be unfeasible for NISQ devices for long time evolution, as the number of gates needed and the length of the circuit grow linearly with the length of time one wants to evolve the state for. More prohibitory, the complexity of implementing a circuit also grows exponentially with the size of the system [136].
There have been some proposed solutions to cut down the gate count of Trotterization, mainly focusing on compressing the gates needed [137], and on mitigating the errors from using a smaller amount of trotter steps [138, 139]. Regardless, we would probably need to wait for fault-tolerant quantum computers, or at the very least quantum computers with much better qubit quality, before Trotterization is able to be implemented with high fidelity [140, 141].
Current NISQ platforms
For quantum computing hardware, DiVincenzo outlined five key criteria to assess the suitability of the hardware for quantum computation tasks. DiVincenzo’s five criteria [142] include:
-
A scalable physical system containing well-defined qubits.
-
The ability to deterministically initialize the system into a well-defined initial state.
-
A set of universal quantum gates, such as single-qubit and entangling two-qubit gates.
-
Qubit decoherence times are much longer than gate times.
-
The ability to perform measurements on the qubit state with high accuracy.
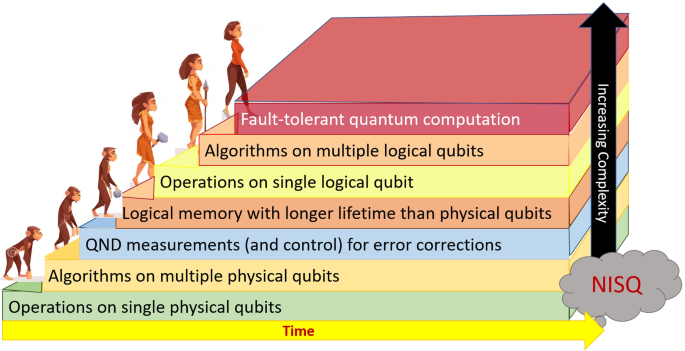
Progress and developments in these criteria help us progress towards building a fault-tolerant quantum computer. But until the quantum computing hardware fully satisfies all the criteria to the point where we can easily scale up the number of qubits and still have error rates low enough to implement error correction codes, we will be in an intermediate stage of the development of quantum computers. It is useful to think of this development as a series of stages. An illustration of how the different stages look like and how they build upon each other is shown in Fig. 5.
Figure modified from [143]. As we progress in time, we hopefully will be able to progress from the lower stages to the higher stages, building on the foundation those earlier stages gives us. The best platforms right now are somewhere between the third (Quantum Non-Demolition measurements) and fourth (logical memory) stages, where computers are starting to be able to perform error correcting codes to build logical qubits from physical qubits. Except for the last two stages which herald the start of the fault-tolerant era, all previous stages of development generally belong to the NISQ era. We also point out that progressing from a lower to higher stage does not imply that no further work must be done to improve the techniques required for lower stages. For example, improving the control of the operations on single physical qubits should be a goal during the entire timeline of development, even after logical qubits replace physical qubits in computation
All the different platforms have unique strengths and weaknesses with respect to the criteria given above. Hence, it is still unclear which is the preferred platform, especially for NISQ computation. We describe the main platforms that have seen the most success so far below.
Superconducting qubits
Superconducting qubits [143,144,145,146] are the current leading candidates in the race for large-scale quantum computation [147,148,149]. They are unlike other microscopic models of quantum computation in that they are constructed out of electrical circuit components such as capacitors, Josephson junctions and inductors. These qubits take advantage of the phenomena of superconductivity [150] and the Josephson effect [151,152,153] to emulate the energy level structure of a 2-level system, thus transforming the circuit into an artificial atom. The field started with 3 basic types of superconducting qubits which were the charge, flux and phase qubits. The performance of these qubits saw improvements as the techniques of fabrication, measurement, and material-based coherence were studied and improved. Further diversification in the type of qubits came with quantronium [154], transmon [155] and fluxonium [156] qubits which are constructed of the same components but seek to improve performance by reducing decoherence and improve upon the robustness of the hardware designs.
Recent demonstrations of high fidelity qubits and gates from major technology players such as Google [41, 157,158,159] and IBM [43] have elevated the superconducting platform as one of the primary choices for demonstrating NISQ era advantage. Current state of the art superconducting qubit hardware uses multi-step processes to fabricate the qubit on thin films of superconductors such as aluminium or niobium. These devices are placed in a conductor to provide electromagnetic insulation and kept in thermal contact with ∼ 10 mK stage of a dilution refrigerator [160]. Further, they are coupled to microwave resonators which facilitate control operations on the qubit using microwave signals [161]. The best superconducting devices are now able to achieve coherence times nearing a millisecond [162], while gate types are typically in the order of tens of nanoseconds [149] and gate fidelities usually around 99.5−99.9% [163, 164]. Despite much hype that these future devices, current NISQ demonstrations are unable to outperform the best classical computers in all scenarios except sampling solutions of a random circuit. However, a computational advantage seems within reach with improvements in the number and quality of qubits.
Google, in 2019 [41], reported the first demonstration of quantum supremacy using their quantum processor named Sycamore which constitutes of 53 transmon-type qubits. The qubits were individually controllable and the processor enabled turning on or off nearest neighbour 2-qubit interactions using 86 couplers. The task that this processor performed was that of sampling the output of a pseudorandom quantum circuit; this choice was based on the fact that the time taken by the best classical algorithm to perform the simulation of the random circuit sampling would scale exponentially in the number of qubits. Google claimed that the Sycamore processor performed the target computation in 200 s, and estimated that the best classical supercomputer running the most efficient algorithm would take 10,000 years to achieve the same result. This result has been followed by other demonstrations [157,158,159] where the particular task is assumed to be beyond the reach of best classical processors and performed on quantum processors with increasing number of qubits. Yet, admittedly we need to acknowledge the immense advancement in the science and technology of superconducting system in recent years.
Other than small-scale version of quantum algorithms such as Deutsch-Jozsa, Grover search [29] and Shor’s algorithm [165], NISQ algorithms like VQE have been run on superconducting computing hardware. The ground state energies of molecules including H2 [166], LiH and BeH2 [167] have been approximated with VQE methods on such hardware. The QAOA algorithm was also demonstrated in [168] using a 19-qubit superconducting processor.
Superconducting qubits have also seen some success in quantum simulation, where qubit-based hardware is used to simulate a quantum system to study its properties. The key idea is to mimic almost exactly the time evolution of the quantum system of interest with control-gate operations in a quantum circuit. Digital and analog simulation are the two sub-routes being explored with superconducting qubits. The digital scheme has been applied in the case of superconducting qubits by making use of the Jordan-Wigner transformation which maps Fermionic operators to Pauli operators [133]. Circuit QED-based digital simulation with transmon qubit setups were shown in [169, 170]. Further, an adiabatic algorithm was digitally simulated using up to 9 qubits and 1000 quantum gates in [132]. These examples show remarkable progress in digital simulation; however, the accuracy required for scaling up remains challenging due to gate errors. Substantially reducing gate errors constitutes a current challenge for digital simulation.
There have also been many proposals to use superconducting qubits in analog simulation as well. By tuning the parameters such that we physically mimic a complex many-body Hamiltonian with the hardware. An array of coupled superconducting qubits was used in [171, 172] to emulate the interactions of ultra-strong and deep-strong coupling regimes of light-matter interactions. Quantum walks of one and two strongly correlated microwave photons were demonstrated using a 1-D array of 12 superconducting qubits with short-range interactions in [173]. Open quantum system-related problems such as the Spin-Boson model were also realized using superconducting qubits coupled to an electromagnetic environment in [174]. Such analog simulation suffers from the same issue of finite coherence of qubits and gates, but approaches which model the environment’s interaction using noisy channels are being further explored.
Finally, we also must mention advances in quantum annealing where progress has been made with ∼ 2000 superconducting qubits on a chip manufactured by D-Wave Systems to simulate 3D Ising spin lattices [175, 176], out-of-equilibrium magnetization in frustrated spin-chain compounds [177] and coherent quantum annealing in a 1D Ising chain [178].
Trapped ions
An ion trap refers to the use of electromagnetic fields and laser cooling to control the spatial position of ions and consequently reduce the temperature of the ions. The scheme was suggested just a year after Shor’s algorithm in 1995 [179]. Early experimental implementations, especially demonstration of their entangling capabilities, soon followed [180, 181].
The main idea behind trapped ion technology is to use the two different internal states of the trapped ion as the two-level system. Thus, a quantum computer could look like an array of trapped ions where each ion is effectively treated as a qubit. Some possible internal states that can be used include states of different orbital angular momentum, the fine structure states of the ion or the hyperfine states of the ion. The resultant qubits are respectively called optical qubits, fine-structure qubits and hyperfine qubits. One can even add an external magnetic field to split the different magnetic sublevels with the same orbital angular momentum and use those states, with the resultant qubit being known as a Zeeman qubit. These different qubits have their own strengths and weaknesses. Single qubit gates on the qubits can be implemented by driving Rabi oscillations on the ions through resonant laser pulses [182], whereas two-qubit entangling gates can be performed by manipulating the motional degree of freedom of a chain of ions in the trap together with the internal states of the qubits [183]. State preparation is done by optical pumping to a well-defined electronic state. Qubit measurement is done by exciting one of the qubit levels to a higher level auxiliary short-lived level and detecting the fluorescence, which can be performed to a very high fidelity [184]. It is known that state preparation, qubit measurement, single-qubit and entangling two-qubit gates can all be performed with fidelities higher than what is required for quantum error correction [185,186,187]. Lastly, ion coherence times are much longer than gate times, where the coherence times range from 0.2s for optical qubits [188] to up to 600s for hyperfine qubits [189]. On the other hand, single-qubit gates times are on the order of a few microseconds, and two-qubit gate times are typically on the order of 10−100 µs. It can be seen that trapped-ion technology for a quantum computer easily fulfils all 5 points of the DiVincenzo criteria.
Trapped ion quantum computers have registered reasonable success. Small-scale, fully programmable trapped ion quantum computers have been developed [190,191,192,193]. Small-scale demonstrations of fault-tolerant algorithms like the Bernstein-Vazirani algorithm [194] and Shor’s algorithm [195] have been achieved on the platform, along with NISQ algorithms like VQE [196]. Analog simulations of spin and spin-boson models have also been performed on larger trapped ion arrays [197,198,199].
However, there are certain weaknesses with trapped-ion technology. Firstly, even though gate times are shorter than the coherence times, the gate times are long compared to other quantum computing platforms, e.g. superconducting platform where gate times is done in around 10 ns. Hence, quantum algorithms with a large number of gates will take a comparatively longer time to run on these trapped ion quantum computers. Furthermore, scaling up the system to a larger number of qubits is quite a challenge for trapped-ion technology. It is difficult to address and measure a large array of ion qubits with bulk optical components, since a large number of these bulk optical components will be needed. This problem also challenges scalability of the system. Furthermore, since two-qubit operations are done by manipulating the motional states of a chain of ions, it becomes harder to control the motional degree of freedom as the number of ions in the chain increases. The decrease of the Lamb-Dicke factor as the system size increases also means that two-qubit operations will become slower, although there are proposals to move out of the Lamb-Dicke regime [200].
Some companies have already started to commercialize the technology behind ion trap quantum computers, such as Honeywell and IonQ. Benchmarks for the IonQ quantum computer can be found in [193]. As compared to other commercial platforms such as Rigetti and Google, the IonQ quantum computer has a smaller number of qubits, yet arguably the qubits in the IonQ computer are of higher quality, as quantified by the single qubit and two-qubit gate fidelities. Some good reviews on trapped-ion quantum computing can be found at [201, 202]. A discussion on the material challenges such a platform faces can be found here [203], and a pedagogical discussion on the experimental techniques can be found in [204, 205].
Photonics
Optical quantum systems have always been prominent candidates to realize quantum computing right from the start [206]. They utilize the knowledge in the mature field of quantum optics to manipulate quantum states of light to perform quantum computations.
Photonic platforms inherently have some experimental advantages over other platforms. For example, the quantum information is typically encoded in the photons. Photons do not interact much with each other nor with the environment. They are thus potentially free from most decoherence. Unfortunately, this is also its downside, as it is hard to get individual photons to interact with each other, and thus, it is hard to implement two-qubit quantum gates. Initial proposals to introduce interactions between photons revolved around two main proposals: either representing n qubits as a single photon in 2n different modes/paths [207], or using non-linear components, like a Kerr medium [208, 209]. Such methods were either not scalable, in the case of the first proposal, or extremely hard to implement experimentally, in the case of the second proposal [210].
In 2001, Knill, Laflamme and Milburn showed that, in principle, universal quantum computing was possible on a photonic platform, with just beam splitters, phase shifters, single photon sources and photon detectors [211]. This is a notable result as it does not require the use of the non-linear couplings between optical modes, except perhaps during the preparation of initial states, making it much easier to implement experimentally. Nonlinearity can of course be induced with post-selection, but this option makes the scheme probabilistic. The protocol, known as the KLM protocol, however also shows that such a platform needs an exponential amount of resources to overcome the probabilistic nature of linear optics.
Therefore, photonic quantum computers continue to be plagued with significant scaling problems, mostly stemming from the fact that the KLM protocol is largely probabilistic in nature. Since it is hard to produce single photons deterministically (see Section 5.4), it also means that any quantum computer would struggle with either reliably generating single photons on a large scale, or reliably combining them into larger quantum states. One alternative proposed is to utilize Gaussian states, or in other words, squeezed states of light that are not comprised of single photons, which are experimentally much easier to control [212]. This method is closely linked to continuous variable quantum computation, which is a form of quantum computing that relies on infinite-dimensional Hilbert spaces, instead of qubits with a finite-dimensional Hilbert space. More information on the continuous variable approach can be found in [213,214,215].
Due to certain technical differences between photonic quantum computers and other quantum computing platforms, the development of photonic quantum computers, especially in the last 5 years, is closely linked with the development of the boson sampling/GBS algorithms. While we expect that a fully developed photonic quantum computer will be universal and able to execute any quantum algorithm, to date, most experiments on photonic platforms are variants of boson sampling/GBS [216]. Yet with just boson sampling, as mentioned in Section 5.4, photonic quantum computing has proved to be one of the first few platforms to claim quantum supremacy [42]. Indeed, integrated photonic chips can be applied easily to artificial neural networks [217, 218] and quantum key distribution [217, 219]
Some companies have started to commercialize the technology behind photonic quantum computers. For example, Xanadu has developed a full-stack hardware-software system for an integrated photonic chip, which is capable of running algorithms on photonic chips that require up to eight modes of squeezed vacuum states initialized as two-mode squeezed states in a single temporal mode, and a programmable four-mode interferometer [220]. While their first photonic chip is small compared to larger photonic platforms (such as the ones used in large scale GBS experiments like in [42, 117]), they believe that such a platform is easily scalable, especially with recent advances in chip manufacturing technology, while retaining its ability to be dynamically programmed. Recently they announced a photonic processor that is capable of performing a GBS experiment on 216 squeezed modes with the help of a time-multiplexed architecture [44]. One should also note that photons are excellent platform for quantum communications [219, 221, 222]. Some good reviews on photonic quantum computing can be found at [212, 223, 224]. A good experimental discussion on how we might be able to construct a scalable photonic quantum computer can also be found at [225].
Other platforms
Other than the three platforms mentioned above, there exist many other proposals to build a quantum computer. However, the majority of these platforms struggle with scaling their platforms past a few qubits at this point. Some notable examples, and by no means exhaustive, are:
-
Nuclear magnetic resonance (NMR) quantum computers. Such devices utilize the spin states of nuclei within chemical molecules as qubits. While this platform was promising during the early stage of quantum computers [226,227,228], especially since it shares many experimental techniques with the well developed field of NMR spectroscopy, the technique has largely fallen out of favour due to the natural limitations on scalability and long gate implementation times. Good reviews can be found at [229, 230].
-
Quantum dots that rely on electron spin. Such devices work by confining free electrons or electron-holes in a small space in a semiconductor and by doping the material with atomic impurities. Qubits are encoded in the spin of the electron. Recently, it has been shown that at ‘hot’ temperatures (above the micro-kelvin level), qubits in such devices have long lifetimes [231]. Also, one- and two-qubit logic gates [232,233,234] can be constructed. While this is promising, proof of scalability is yet to be shown. Good reviews can be found at [235,236,237].
-
Rydberg atoms. Such devices work by trapping cold atoms in optical lattices generated by counter propagating lasers. By utilizing the strong interactions between cold atoms in Rydberg states, certain quantum logic operations can be performed. This approach has found some success in analog quantum simulations for simulating many-body dynamics [238,239,240,241,242], with simulations of up to 256 atoms possible [243]. While none of the simulators so far are capable of universal quantum computation yet, the field is moving rapidly and a recent work suggests a proposal for making the system into universal quantum computer [244]. Good reviews can be found at [245, 246].
Current applications
While current quantum computers have barely started to claim quantum supremacy [41, 42, 247], it is noteworthy that their computational advantage has only been demonstrated for ‘custom-built’ problems that are only meant to demonstrate their theoretical computational advantage, with no known practical applications. It is therefore still an open question if a NISQ computer can ever obtain an advantage over classical computers over a ‘killer’ application that is relevant to the industry or science.
In the NISQ era, we do not expect quantum computers to become general purpose computing devices. Indeed, most quantum computers are likely to be accessed through cloud services, providing niche usage within a larger computational algorithms. These niche usages are probably harder on classical computers and one could hopefully achieve substantial quantum speedups over classical computations.
We list a few fields where the most promise for potential quantum speedups is believed to exist.
Quantum simulation
As mentioned previously, one of the push factors behind the search for quantum computers stems from the hope that such devices could simulate quantum many-body systems that could be highly entangled and therefore not easily tractable on classical computers [4]. Richard Feynman in fact suggested this advantage. With classical computers, the fields of chemistry and physics are constantly faced with limitations on the number of molecules and atoms that can be efficiently simulated on such system. Thus, quantum simulation has stubbornly remained one of the core applications of quantum computers.
Broadly speaking, such problems usually fall under two broad classes: those that solve the spectrum of a given Hamiltonian, or those that study the dynamics of a quantum state under a given Hamiltonian, preferably in an open system.
In chemistry, one of the hopes is that quantum computers can improve the accuracy in the direct simulation of molecules. By so doing, it would allow for more accurate study of important reactions and system that are currently inaccessible by methods relying on classical computers. One of the molecules that has been receiving the most attention is FeMeCo [248, 249], which can give us insights into the designs of new catalysts for nitrogen fixation, a crucial step in the industrial process of producing fertilizer. Strategies for using quantum computers to solve models of strongly correlated electrons, common in chemical problems, have also been proposed [250]. Resource estimations are somewhat optimistic that quantum computers will eventually be able to tackle such problems in the fault-tolerant era [251,252,253], but it must be said that such calculations do not say anything about the NISQ era.
The original proposals hinges on quantum phase estimation to get the molecular energies [254, 255]. However, the quantum phase estimation algorithm is not NISQ friendly, requiring way too many gates to be feasible on NISQ computers [256]. Attempts to overcome this lead to the first NISQ-friendly algorithm, VQE [50], which we have described earlier. Some early applications have applied VQE to the estimation of the energy of water molecules [257] and small hydrogen chains [157, 166], which while small and ‘trivial’ for classical computers, are an important proof of principle step. More detailed studies on the feasibility of applying VQE to chemical problems suggest that it might be possible to obtain quantum advantage with the choosing of good ansatz and can be found here [258].
The potential to improve time-dynamic simulations of chemical systems on quantum computers is also of interest, although comparatively little attention has been paid to it. This is somewhat surprising as it could allow accurate first principles simulation, with the potential to offer new insights into complex dynamical processes, where nuclear states and excited electronic states interact with one another [259, 260]. Early proposals rely mostly on Trotterization [261] (see Fig. 6 for a conceptual illustration), but have been estimated to be too costly to be feasible in the near term [136]. Other early proposals to avoid Trotterization also required far too complicated circuits [262]. As an alternative, VQAs have been proposed to simulate exciton dynamics in molecules [263], and VQS have been demonstrated for small systems [264], although no detailed study has been done on how feasible it would be to scale up such processes. Interesting review papers on the application of quantum computers to chemistry can be found in [265, 266].
Figure adapted from [267]. A conceptual illustration of how one might use Trotterization to perform a quantum simulation on a quantum computer. Given the physical problem of finding the evolution of a state under a Hamiltonian for a period of time, a mapping can be used to encode the relevant details of the problem into qubits on the quantum computer. Then, the encoded Hamiltonian can be sliced into many small steps according to the Suzuki–Trotter formula. By implementing the slices in succession, this gives an approximation for the time-evolved state as its output. By measuring the state on the quantum computer, approximate observables for the physical system can be obtained
In high-energy physics, there is a widespread usage of perturbative methods in quantum field theory. However, there are cases where such perturbative methods break down, for example in quantum chromodynamics (QCD). Classical computational methods to overcome this like Monte Carlo simulations have extremely high computational costs which might be unattainable [268, 269], and the hope is that quantum computers and simulators may be able to overcome this by providing alternate methods for such calculations [270].
Early proof of principle simulations on studying the time dynamics of a toy model on QCD have showed some promise. The analysis is done on both trapped ions as an analog simulation [271] and superconducting circuits using Trotterization [134]. VQS has also been applied for such simulations for system sizes of up to 20 qubits and 15 variational parameters [272]. Methods utilizing both analog and digital quantum simulation methods have also been proposed in the study of weakly driven quantum systems [273]. However, preliminary results strongly suggest that to obtain useful results at the energy resolutions necessary on NISQ devices, significant improvements in algorithms or error-mitigation techniques will be necessary [274].
Calculations of ground-state energies are also of interest in the field. VQE was first applied to this field by calculating the binding energy of deuteron on superconducting devices [275]. Subsequently, VQE experiments applied to this field were also performed on trapped ions [276] and subnucleon calculations of two and three body forces between heavy mesons were performed on photonic platforms [277]. There is currently much work in improving similar computations [278, 279] and in studying what types of variational circuits might be useful for these tasks [280]. Quantum neural networks have also been proposed to aid in analysing the data generated from high energy physics experiments [281, 282]. Interesting review papers on this field can be found here [283, 284].
The two topics covered in some detail above, chemistry and high-energy physics, are by no means exhaustive. It is also important to mention that the technology underpinning quantum computers lend themselves naturally to analog simulations of strong correlated quantum matter [172, 285, 286]. Other interesting applications of quantum simulation include material design [287] and quantum control [288] and nuclear physics [289, 290], and so forth. Interesting overall review papers on quantum simulators can be found here [267, 291].
Machine learning
The field of machine learning deals with the question of how to build computers that can automatically learn through experience, without needing to be explicitly programmed to solve problems [292]. It is one of the fastest growing fields today and it has been shown to be particularly useful for uncovering hidden relations between complex and high dimensional data sets that might otherwise be far too hard to compute [293, 294]. With its widespread industrial application now, it is only natural to wonder if quantum computers could also be used for machine learning tasks, and if any quantum speedups are expected, especially since there are limitations of the standard classical computing paradigm [295].
Early works to produce a learning algorithm for quantum computers have already showed that such a quantum machine learning model could be able to accomplish things that no classical algorithm are capable of doing, with regard to the capacity storage of associative memories in the machine learning model [296, 297]. It has also been hypothesized that with fault-tolerant quantum computers, pattern identification algorithms could be designed that quantum machine learning may have exponential speedups over classical counterparts [298], which has spawn much theoretical studies on how quantum and classical learning differ [299, 300].
Generally speaking, there are two main approaches to the use of quantum computers for machine learning tasks. The first method is to use existing classical machine learning algorithms. But, it may be necessary to speed up numerical subroutines like sampling [301, 302], matrix inversion [303,304,305,306] or searches [307,308,309] with the quantum computer. However, most of these algorithms rely on quantum algorithms such as the Harrow-Hassidim-Lloyd algorithm or the Grover search. Beyond the size of a few qubits, these algorithms rely on very complex circuits that are not NISQ friendly, preventing them from being scaled up currently.
The second method is to utilize VQAs as machine learning models. These methods usually revolve around the optimization of the parameters of a PQC such that when data is encoded as a state in the computational basis, after being acted on by the optimized PQC, a measurement of the qubits then gives us suitable labels for the data [310,311,312]. This approach has gained some success [61, 168, 313,314,315,316], with a notable advantage being their improved expressibility over classical models [317], but the trainability problems present in VQAs still persist, and there are questions on their power to generalize [70, 318, 319].
Much work has been done on investigating how quantum machine learning models scale [320, 321], on how the properties of the quantum settings actually change the problem [322, 323], and on the type of problems that show quantum speed-ups [324,325,326,327]. While there is a lot of hype surrounding quantum machine learning, important questions are being raised on how practical quantum machine learning models will evolve [319, 328].
The field has shown exponential growth in the past decade, and some good references to get a more in depth overview can be found here [329,330,331,332].
Numerical solvers
Quantum computers have been shown to be theoretically capable of obtaining quantum speedups for certain numerical solvers. Most famously, the HHL algorithm, which is a quantum algorithm that obtains the inverse of a large matrix under certain conditions, promises an exponential speedup in solving the linear system problem Ax=B relative to any classical solver run on a classical computer [333]. This algorithm originally attracted a lot of attention and improvements [334, 335], as it promised to solve what is called a BQP-complete problem. That is, any problem that is solved on a quantum computer efficiently (in polynomial time with high probability) can be simulated with this HHL algorithm. It has been demonstrated for an 8×8 matrix [336]. However, the complexity of the circuits needed for the HHL algorithm is expected to require fault-tolerant computers to be able to implemented successfully for large matrices. As an alternative, NISQ-friendly algorithms for solving the linear system problem that rely on VQAs [337, 338] were proposed, but they also suffer from the barren plateau and trainability problems described above. Quantum-assisted methods have also been applied to this problem, and they have demonstrated capabilities to solve classically solvable systems of up to 2300×2300 [339].
Other than the linear system problem, quantum computers do show promise for quite a few other numerical solvers:
-
Typically, solving non-linear differential equations on classical computers require large amounts of computational resources [340]. Quantum algorithms hope to alleviate this by reducing the amount of resources needed, potentially allowing us to efficiently solve more complicated non-linear differential equations for more and stronger non-linearities. VQAs have been extended to solve such problems, with proof-of-principle results for a simple 1-dimensional time-independent non-linear Schrödinger equation obtained on superconducting qubits [341]. This method relies on complex controlled unitaries and multi-qubit operations, along with ancillary qubits, which can be quite expensive on NISQ devices. Alternatives using the quantum-assisted approach that do not require such operations have been proposed [342], and have been demonstrated for up to 8 qubits. Other ideas like differentiable quantum circuits [343] have also been proposed, and there is very strong interest in using such NISQ algorithms to solve the Navier-Stokes equations [344, 345].
-
Factoring has always been a focus for quantum computing, especially since Shor’s famous algorithm to efficiently prime factorize large numbers [12]. It has been shown that the problem of factoring can be mapped to the problem of finding the ground state of an Ising Hamiltonian [346,347,348]. This has naturally lead to proposals to solve the factoring problem with variational principles, with QAOA being used in [349]. A detailed analysis of such a scheme is done in [350], with the conclusion that at this stage, certain types of noise still heavily affects the computation.
Combinatorial optimization
Combinatorial optimization problems are specified by n bits and m clauses, and the goal is to find a n-bit bitstring that satisfies as many such clauses as possible. Many famous problems, like the travelling salesman problem [351] and the knapsack problem [352] belong to this category. All combinatorial optimization problems can be re-framed as the problem of maximizing the expectation value of a diagonal Hamiltonian written as
where in the definition of Cj,j1,…jp is some subset of {1,2,…n}. Clearly, Cj has an expectation value of 0 with respect to some n-qubit computational basis states and 1 with respect to other n-qubit computational basis states, depending on the values of j1,…jp in the product. Hence, we can use the operator Cj to encode the jth clause that a bitstring must satisfy, and the bitstring k that maximizes the expectation value of Hc would be the computational basis state |k〉 that satisfies all of the clauses, i.e. 〈k|Cj|k〉=1 for all j.
One such combinatorial optimization problem, known as the Max-Cut problem [353], attracted much attention in the quantum computing community early on. The Max-Cut problem is usually mathematically portrayed as the problem of partitioning the nodes of an undirected graph into two sets, such that the number of nodes connecting both sets is maximized. This problem is known to be NP-complete [354, 355]. Using the abovementioned method, we can cast the Max-Cut problem as the problem of maximising the diagonal Hamiltonian
In Hc above, the summation is done over all edges 〈jk〉 between the j and k nodes, and the clause C〈jk〉 is maximized when the j and k nodes belong to different sets, i.e. when the expectation value of C〈jk〉 is taken over a computational basis state that has different values in the jth and kth bit. As mentioned in section 5.3, the QAOA algorithm was introduced in the context of solving the Max-Cut problem, and since then, the QAOA problem has been demonstrated for up to 19 qubits [168]. There has also been plenty of follow-up work on the QAOA algorithm for the Max-Cut problem [356, 357]. It has also been theoretically shown that under certain conditions, the QAOA algorithm beats the best classical algorithms [358] for the Max-cut problem. However, these conditions are somewhat strict, and outside these conditions, where one may hope for quantum advantage to be demonstrated, it is not clear if classical methods for the Max-cut problem are inferior [359].
Outside the Max-Cut problem, other combinatorial optimization problems that have been investigated with quantum computers are protein folding [360,361,362], the knapsack problem [363], graph colouring [364], and the k-clique problem [365], to name a few.
Outlook
Quantum computers have received plenty of hype in the past two decades, as they promised to solve certain hard problems which no known classical algorithms can solve efficiently. What makes this even more significant is that those hard problems, like prime factorization, have deep implications in many sectors and they can potentially disrupt entire technology industries. They also contain potential implications for national defence. Both reasons have caused national research agencies and tech giants to pour money into their own quantum computing departments.
However, solving those really hard problems will probably require fault-tolerant quantum computers, which is not likely to be realized for quite a while. Such quantum computers require enormous leaps in both experimental control techniques over the qubit gate operations, and the amount of qubits available. While there is no reason why we will not eventually be able to construct such devices, and experimental progress in the last few years gives cause for optimism, it is undoubtedly a tough undertaking to build a fault-tolerant quantum computer, and it will probably take another decade at minimum.
Regardless, the rapid developments in both technology and theory in this field are exciting. We would like to point out that, while comparisons between the eventual capabilities of quantum and classical computers are fair, it took a long time for classical computers to come this far. Quantum computers by comparison have not had as long as a runway to demonstrate their effectiveness. As described at the start of this work, it took many decades from the time that the first computational devices were envisioned to then develop a rigorous theoretical framework allowing understanding of the power of computers. And then it took a global war to provide the impetus to build a classical computer capable of running a ‘killer app’, which was the capability to break German cryptographic codes. And even then, when the supremacy of computers over classical decryption was demonstrated, it still took 2 decades and the development of the transistor before computing finally emerged into its own. While we live in the information age and are used to rapid technological payoffs, quantum computing seems to be bucking the trend. Rather than saying that quantum computing is not feasible and will never provide substantial payoff, we believe that we need to be a little optimistic and level-headed when evaluating our short and medium term expectations from the field.
Instead of buying into the hype (and encouraging it), we, as scientific professionals, should instead present the current accomplishments of the field. We should not over- nor under-sell the potential of quantum computing. While the process of judging the field will inevitably be subjective to a large extent, and dependant on individual opinion and interpretation, we hope that the majority are able to agree on a few general points:
-
NISQ devices are impressive technological devices in their own rights, being capable of demonstrating a form of quantum advantage over classical computation methods for extremely specific problems.
-
There are a few platforms that have seen the most success. Each platform has inherent advantages and disadvantages and it is too early to tell which will be the most promising in the long term.
-
Due to the limitations of NISQ devices, it is not useful to think in terms of fault-tolerant algorithms (or at least mainly in such terms), as they probably will be unimplementable on such devices.
-
Separate, NISQ-friendly algorithms will need to be developed for such devices. A heavier reliance on analog computing as opposed to digital computing might also be necessary.
-
Unlike fault-tolerant algorithms, it is not known if quantum advantage for actual problems that are of interest outside the quantum information community (such as optimization and Cryptanalysis) is achievable, and even if so, under which conditions. As such, there are no ‘killer apps’ achievable as of yet. Certain fields like quantum simulations and machine learning have been singled out as showing the most promise of breakthroughs, but quantum computers and NISQ algorithms are still far from industrial applications.
-
Even so, the field is worthy of investment, as no one can predict where and when a major breakthrough might occur. Furthermore, greater accessibility to quantum computers and technologies will create a positive feedback loop, with more scientists being able to get a feel for quantum computing, their strengths and limitations, and allow them to think of potential applications.
While we do not want to be detracted from the accomplishments that NISQ computers have achieved, we want to stress that developments in NISQ devices, both theoretically and experimentally, should not lose sight of the long-term goal: to develop the core techniques needed to quicken the pace towards fault-tolerant quantum computers. This is especially so as we do not expect that NISQ computers will lead to truly transformative and disruptive technological developments. Most likely, fault-tolerant quantum computers will be necessary eventually. However, nobody knows how long it will take to get there, and the odds are that it is still at least a decade away, if not more. Thus, this NISQ era, while maybe unwanted and unexpected, is the reality that we have to live and work with. Many relevant and interesting research questions exist in the NISQ field, and it is important for the community to work on such problems.