Digital transformation (DX) has been rapidly developed in recent years, and an era in which every physical object will be connected to the Internet is fast approaching. In such an era, new value will be created through information processing in cyberspace, leading to the prevalence of new services such as automated driving, telemedicine, digital twins, and drone transportation networks.

 However, constructing the infrastructure required for the realization of these services remains a major issue. Trillion sensors will be required for data collection, and data sensors relying primarily on AI must be designed for data processing. The development of optical communications, photoelectric interfaces, and 5G and 6G wireless technologies will also be crucial. As such, the information technology industry corresponding to DX has steadily expanded along with the market for semiconductors, the primary “building blocks'' of this industry. A major technological problem concerning semiconductors is that the performance of conventional materials, such as silicon, is reaching its limit as illustrated by the breakdown of Moore’s Law. The exponential improvement of device operating speeds has slowed considerably in recent years, and the rapid increase in power consumption is becoming increasingly serious.

 Quantum materials are a field in which novel quantum concepts are realized to fabricate functional materials that present a considerable improvement in performance over existing technologies such as semiconductors. Beyond CMOS circuits, quantum bits, photoelectric conversion devices, nonvolatile memory, and quantum sensors are just some examples of quantum materials being actively studied and developed with the aim of innovating the infrastructure required to support DX as information processing, transmission, storage, and collection units.

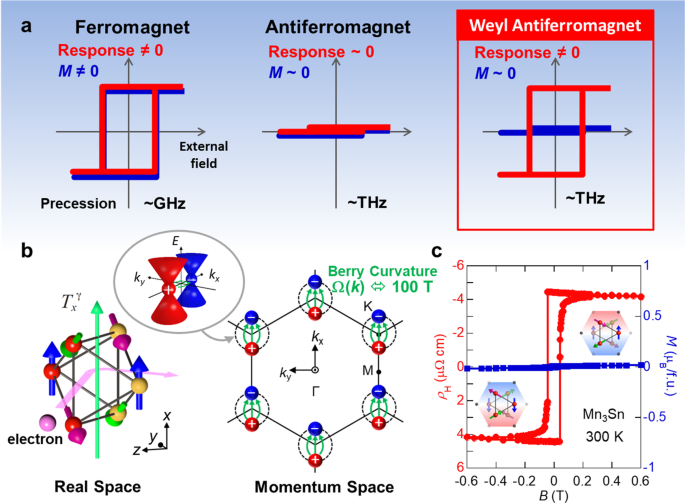
This review article presents the recent highlights of studies on Weyl magnets and other topological magnets, which have gained global interest as examples of quantum materials. Their existence was theoretically proposed in 2011 [1], and ever since our group pioneered research by developing them experimentally [2,3,4,5,6,7], the number of such examples has been increasing [8]. Here, “quantum” indicates that the quantum phase (Berry phase) of the wavefunction is controlled through the topology of the band structure. This has led to the discovery that previously undiscovered properties arise in alloys made of inexpensive materials such as iron and manganese. The most significant example is the discovery of giant transverse responses in antiferromagnets, which have never been implemented in any conventional application (Fig. 1a). Antiferromagnets are indispensable for the high-density and ultrafast operation of information carriers required for future DX, due to their lack of a stray field and their THz operating speeds [9,10,11,12]. This paper presents the detailed properties of how Weyl antiferromagnets, first discovered by our group, can manifest a colossal anomalous Hall effect previously considered absent in such materials, and are paving the way for future development in the field of quantum materials (Fig. 1a).

Additionally, the effective use of unused heat below 200 °C is highly desirable to achieve carbon neutrality by 2050. The magneto-thermoelectric effect (anomalous Nernst effect) is a promising method of converting waste heat into electricity [13, 14]. Our recent studies have demonstrated that the magneto-thermoelectric effect can be enhanced by an order of magnitude by taking advantage of the topology of the electronic structure [7, 15, 16], allowing metallic alloys to be actively employed as thermoelectric materials, a field thatwhich has been dominated by semiconductors thus far [14]. Metallic alloys have the advantage over conventional materials in that they allow a simplification of the structure of thermoelectric modules, leading to an unprecedented reduction in production costs. This enables the low-cost production of heat fluxow sensors for visualizing energy flows, which is fundamental to achieving carbon neutrality. Depending on future improvements, thermoelectric modules may have the potential to act as stand-alone power sources for trillion sensors in the IoT era [16].

Topological magnets thus present significantly better performance than conventional magnets and can be implemented in various applications. In this review, we focus on topological magnets, which have nontrivial topology in their momentum space electronic structure. There is another class of topological magnets that have topological texture in real space, such as non-coplanar spin texture and skyrmions, which have attracted much interest worldwide. However, due to space limitations, we will not discuss the latter in this article. The following section briefly introduces Weyl semimetals and Berry curvature, which are crucial for understanding the origin of these robust responses. We then provide an overview of the giant anomalous Nernst effect in ferromagnets, the novel realization of the anomalous Hall effect in an antiferromagnet, and the various possible applications of these effects.

Topological magnets

Fictitious magnetic field in momentum space

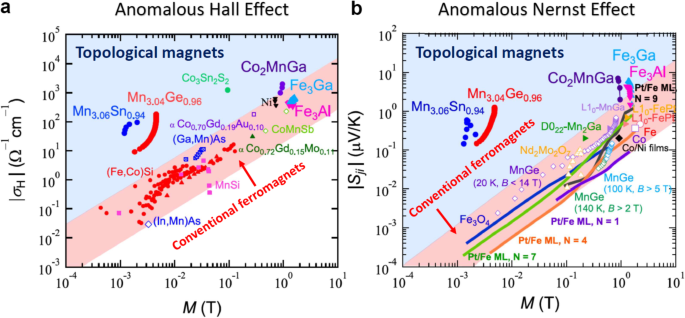
The aforementioned anomalous Hall effect and anomalous Nernst effect were initially discovered in ferromagnets in the nineteenth century [17]; their magnitude is observed to be proportional to the magnetization [18, 19]. The sizes of the anomalous Hall and Nernst effects increase in proportion to the magnetization in many ferromagnets, as shown in Fig. 2 [20]. Topological magnets such as Mn₃Sn and Co₂MnGa, which are introduced in this paper, do not follow this trend, and are found to have anomalous responses that are several orders of magnitude larger than those expected from their magnetizations [7, 15, 16]. This remarkable enhancement is attributed to the topology of the electronic structure in momentum space and the resulting fictitious magnetic field [21].

The first example of a phenomenon brought about by the topology of electronic structures is the quantum Hall effect, which was discovered by von Klitzing et al. [22] in 1980, approximately 100 years after Edwin Hall’s discovery of the Hall effect [17]. 2 years later, Thouless et al. [23] clarified that the quantum Hall effect can be understood as the quantization of the conductivity to an integer multiple of e²/h, when the flux of a fictitious magnetic field (Berry curvature) through a two-dimensional electron surface becomes an integer multiple of 2π; they were awarded the 2016 Nobel Prize for Physics for this discovery. An important distinction to make is that whereas the ordinary Hall effect can be understood as the result of an external magnetic field (in real space), the quantum Hall effect is caused by a fictitious magnetic field (in momentum space).

There is a clear duality between the magnetic field in real space and the fictitious magnetic field in momentum space, in that both act as quantum phases on the electron wavefunction. A typical example of this for the real space magnetic field is the Aharonov–Bohm effect. If we consider an electron whose time evolution of its position takes the form of a closed orbit, the phase of the electron wavefunction is determined by the magnetic flux passing through any closed surface enclosed by the orbit. The same effect can be seen for the fictitious magnetic field in momentum space. The motion of a conduction electron in a conductor is described as the time evolution of its momentum on the band structure defined in momentum space. As in the real space case, the phase of the electron wavefunction is determined by the fictitious magnetic flux (created by the fictitious magnetic field) passing through the closed surface enclosed by the electron orbit in momentum space.

Thus, the fictitious magnetic field is significantly affected by the geometry of the electronic structure, i.e., its topological character. Particularly in the twenty-first century, materials science has undergone a paradigm shift caused by the discovery of the topological properties of electronic structures. However, most research developments - such as those on graphene, topological insulators, and Weyl semimetals in Europe, the US, China, and other countries [8, 24,25,26] - have been limited to weakly correlated electron systems, and the topological nature of the electronic structure in strongly correlated electron systems remained completely unknown. Conversely, magnetism is an important property of strongly correlated electron systems and is a field in which Japan has traditionally led the world. Research on how topological electronic structures are realized in magnets, is becoming something of a trend in condensed matter physics. In particular, since the Weyl semimetal state was first theoretically proposed to exist in a ferromagnet in 2011 [1], extensive research has rapidly progressed worldwide [8].

Weyl semimetals

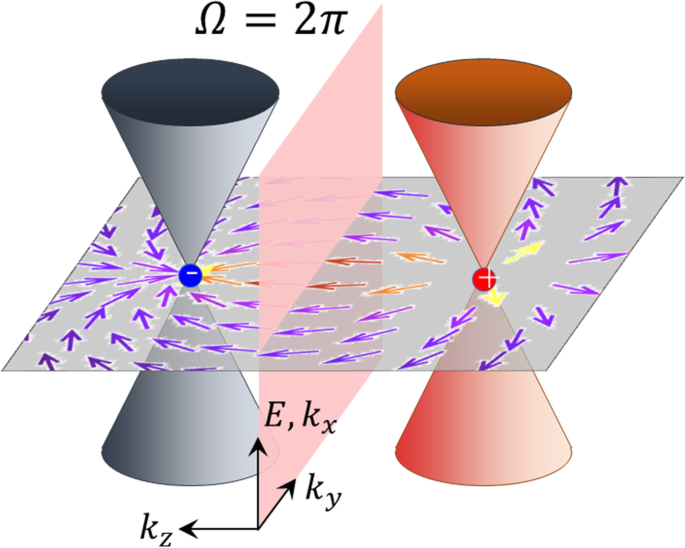
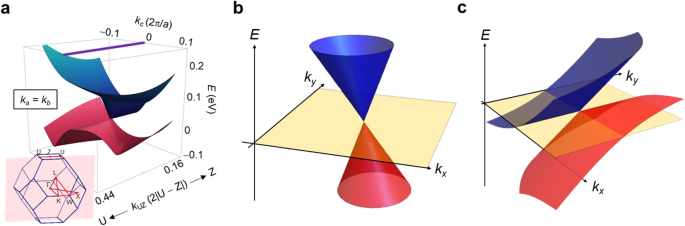
The magnetic Weyl semimetals are an example of a topological electronic phase of a magnet. As the simplest example, the case of a single pair of conical electronic structures with linear dispersion in momentum space will be considered (Fig. 3), and the effects of electron correlations will be ignored [27, 28]. Notably, the intersection of these linear dispersions (Weyl point) serves as a source of the fictitious magnetic field in momentum space, and can be considered a magnetic charge. Analogous to Gauss’s law of electromagnetism, which determines the correspondence between the electric charge and electric field, the magnetic charge located at the Weyl point determines the fictitious magnetic field in momentum space. Weyl semimetals are topological metals hosting the Weyl points near the Fermi energy. When the Weyl points are located precisely at the Fermi surface, the Fermi surface becomes mere points, and an insulating state is realized in the direction connecting the two Weyl points. This direction connecting the magnetic charges determines the properties of the field; if it is along the z direction, the fictitious magnetic field penetrates the two-dimensional electronic system in the xy plane perpendicularly. Since the magnetic charge is quantized, the fictitious magnetic field penetrating this two-dimensional electron surface along the vertical direction is also quantized to 2π, satisfying the conditions for the quantum Hall effect described above (Fig. 3). A Weyl semimetal can be considered a layered structure of such two-dimensional electron systems stacked in the z direction. Thus, a spontaneous layered quantum Hall effect is observed in Weyl semimetals even in the absence of an external magnetic field, which proves to be the intrinsic mechanism of the anomalous Hall effect in such systems. Furthermore, by extending this argument, it can be stated that the fictitious magnetic field in the momentum space itself directly induces the anomalous Hall effect [19, 21].

In general, the origin of the internal magnetic field is the spin polarization of magnetic moments localized at the atomic sites. On the other hand, as mentioned above, the fictitious magnetic field has a different origin, derived from the quantum phase of the wavefunction (Berry phase). Accordingly, the anomalous Hall effect found in Weyl semimetals need not be proportional to the magnetic moment or magnetization as in the case of ferromagnets, but may exhibit behavior that is inherently independent of them. The most striking examples of this were observed by us in the in the antiferromagnets Mn₃X (Fig. 1b) and spin liquid Pr₂Ir₂O₇ [2, 29]. In these compounds, the magnetization was either at least 1000 times smaller than that of a typical ferromagnet, or so small it could not even be observed. Despite this, an anomalous Hall effect larger than that of a ferromagnet was observed, defying the conventional wisdom of the anomalous Hall effect (Figs. 1c and 2a) [20].

As mentioned above, Weyl semimetals have intersections of linear dispersions hosting magnetic charge in the vicinity of the Fermi energy. Therefore, the effects of the Weyl particle, a quasiparticle excitation near the Weyl point, are strongly observed in their metallic conduction properties [20]. In particular, the size of the magneto-thermoelectric effect (anomalous Nernst effect) is directly proportional to the magnitude of the fictitious magnetic field generated by the Weyl particle [21]. The anomalous Nernst effect can be understood as the thermal counterpart of the anomalous Hall effect; although both are transverse electromotive effects, the former is driven by an electric current while the latter is driven by a thermal current. Similar to the anomalous Hall effect (Fig. 2a), it had been empirically accepted that the size of the anomalous Nernst effect is proportional to magnetization, and therefore appears only in ferromagnets (Fig. 2b). This widely accepted notion was overturned by our discovery of an anomalous Nernst effect, approaching the highest values found in ferromagnets, in the non-magnetic Weyl antiferromagnet Mn₃Sn. The remarkable size of the anomalous Nernst effect is attributed to the existence of Weyl points near the Fermi energy (Fig. 2b) [7].

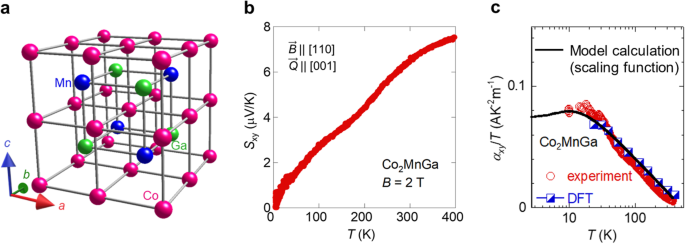
By utilizing these Weyl particles (Fig. 2b), we experimentally demonstrated that the anomalous Nernst effect can be enhanced even further in the full-Heusler ferromagnet Co₂MnGa (Fig. 4), reaching more than 10 times the previous maximum value [15]. The fundamental reason for this enhancement is the appearance of a flat band accompanied by a giant fictitious magnetic field (Berry curvature), which arises as a result of the topological Weyl particles undergoing a quantum Lifshitz transition (Fig. 5a) from type I (Fig. 5b) to type II (Fig. 5c). There is a large density of states in the vicinity of the Weyl points owing to the flat band, which causes a quantum critical phenomenon observed as a logarithmic divergence in the anomalous Nernst effect (Fig. 4c). Independent of our research, enhanced values owing to this criticality have been reported in thin films, and future applications are awaited [30]. Considering Fig. 2b again from this perspective, the significant enhancement in the magneto-thermoelectric effect, as compared to conventional ferromagnets, can be understood as the effects of the fictitious magnetic field appearing on a macroscopic scale. This giant magneto-thermoelectric effect is one of the most important features of topological magnets.

Energy harvesting using the magneto-thermoelectric effect

In the coming era of IoT trillion sensors, it will no longer be possible to replace the batteries of each individual sensor and an independent power supply is essential. Energy harvesting in the range of microwatts to milliwatts is an immediate technological requirement for this power source. Among the various existing energy harvesting technologies such as vibration, solar, and thermoelectric technologies, the thermoelectric alone accounts for approximately half of the current energy harvesting market.

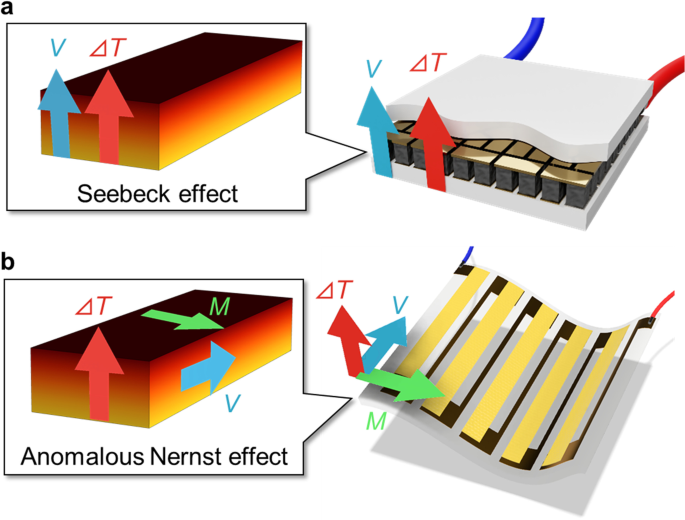
Extensive research has been conducted on thermoelectric materials for more than half a century. Current thermoelectric technology employs the Seebeck effect, and numerous substances have been studied. Despite this, those that can be used above room temperature are still composed primarily of bismuth, tellurium, and lead, which are unsuitable for consumer use due to their high toxicity. Additionally, these compounds are mechanically fragile and vulnerable to vibrations. Furthermore, to achieve a high thermoelectric efficiency using the longitudinal Seebeck effect, a three-dimensionally complex structure must be fabricated using alternating P-type and N-type modules along the vertical direction from the heat source surface (Fig. 6a). Not only is such a complex three-dimensional element expensive to manufacture, it is also difficult to deploy over a large area. Consequently, thermoelectric modules have yet to be widely employed for energy recovery. The magneto-thermoelectric effect can potentially solve these problems in practice (Fig. 6b).

In spite of these difficulties associated with its longitudinal nature, the Seebeck effect is used in thermoelectric modules as sensors for measuring heat flux. Unlike thermometers, heat flux sensors measure the magnitude and direction of the heat flow, which causes changes in the temperature. Accordingly, they are used in various fields ranging from materials science to medicine, for measurements on housing insulation, the heat dissipation performance of electronic materials, and deep body temperature. Additionally, recent progress in microfabrication technology has enabled higher sensitivity, presenting potential for further implementation in biometrics and optical energy measurement. However, these sensors share the same problems as the thermoelectric modules detailed above, in that the fabrication cost is expensive due to the complexity of their three-dimensional structure, with a unit price of several hundreds of dollars per cm². Additionally, the fragility of the material makes it difficult to make the sensors flexible, and the purposes to which they can be applied are still limited.

We have performed extensive research on a new energy harvesting technology, i.e., the transverse magneto-thermoelectric effect in magnets (Fig. 6b). Although the phenomenon itself had already been known, it had been neglected in the development of power generation technology owing to its low thermopower (0.1 μV/K: approximately 0.1 to 1% of a typical Seebeck coefficicient). However, as demonstrated in the previous section,  it is possible to fabricate a substance with a thermopower greater than 10% of that of the Seebeck effect by controlling the topology, or the geometric properties of the electronic structure. Recent discoveries have found that many such compounds are composed of less expensive, more durable, and safer elements as compared to bismuth and tellurium [7, 15, 16, 20]. The magneto-thermoelectric effect is highly compatible with thin-film fabrication techniques due to its transverse nature, offering another advantage in that they allow for greater flexibility in devices. Applying the obtained materials to thermoelectric devices enables the use of the anomalous Nernst effect in thermoelectric applications and heat flux sensors, and the development of this market is just around the corner.

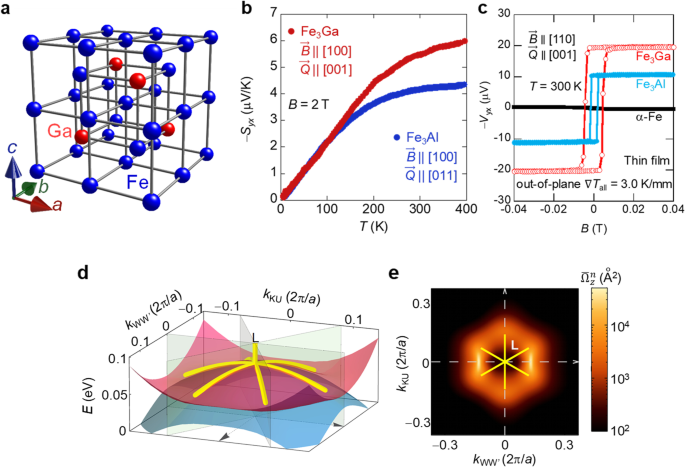
Based on our previous discoveries of a giant magneto-thermoelectric effect in Mn₃Sn and Co₂MnGa, we employed high-throughput calculations to perform first-principles calculations quickly and automatically, in order to identify magneto-thermoelectric materials based on the most inexpensive of the elements, iron. The high-throughput calculation method was used in cooperation with the Arita Group at RIKEN and the Koretsune Group at Tohoku University. Out of the more than 1400 candidate materials found by the calculations, Fe₃Al and Fe₃Ga (Fig. 7a), when doped with 25% aluminum or gallium, were found to exhibit a magneto-thermoelectric effect over 10 times larger than that of pure iron (Fig. 7b, c) [16] among more than 1400 candidate materials discovered in the computation. Additionally, they maintain a high performance over a wide temperature range from 100 to −100 °C and present excellent durability and heat resistance, making them suitable for use in various situations and environments. There have also been reports on the fabrication of Fe₃Al and Fe₃Ga thin films with thicknesses on the order of ten nanometers (Fig. 7c). In the thin film state, not only do both compounds maintain their large magneto-thermoelectric effect, they also record the highest values ever measured without an external field. The power generated is greater than anything possible using conventional technology under the same conditions (area, temperature difference), and their development into thin film devices is greatly awaited.

A detailed analysis of the electronic structure was performed in cooperation with the Ishii Group at Kanazawa University and the Arita Group at RIKEN to determine the origin of this phenomenon. Fig. 7d illustrates the band structure around L without the spin-orbit interaction. The red and blue bands touch at the nodal lines indicated in yellow. Although a finite band gap opens when the spin-orbit interaction is added, the Berry curvature \({\Omega}_z^n\) remains large due to the gap being relatively small (Fig. 7e). The Berry curvature and the density of states increase simultaneously as a result of the spider web-like spreading of the nodal lines, thus greatly enhancing the anomalous Nernst effect.

That the giant magneto-thermoelectric effect appears not only in Weyl semimetals but also in general nodal-line semimetals is of great importance. In particular, the use of versatile and inexpensive iron-based alloys shall further accelerate the development of magneto-thermoelectric devices, such as thermoelectric modules and heat flux sensors.

Functional antiferromagnets and nonvolatile memory

Antiferromagnetic spintronics

Spintronics is a field in which the development of quantum materials plays a crucial role. The term “functional magnets” has long been associated with ferromagnets, and ever since their discovery several millennia ago, they have been used for, among other things, the magnetic needles in compasses. After the birth and development of electromagnetism, it was realized that ferromagnets enabled the generation and transmission of electricity. They have also attracted great interest as magnetic recording materials, following the discovery of the giant magnetoresistance effect and the tunnel magnetoresistance effect in the latter half of the twentieth century. In the twenty-first century, various methods of domain switching using electric current, such as spin-transfer torque (STT) and spin-orbit torque, were discovered [31]. These techniques have led to the development of the nonvolatile magnetic memory STT-MRAM, which has been commercialized recently.

Ferromagnets have a macroscopic magnetization as a result of the magnetic moments at the magnetic atoms aligning in the same direction. Therefore, the direction of the magnetic moment can be easily changed by a magnetic field. Such a change can be detected by a voltage measurement due to the magnetization dependence of the large anomalous Hall and magneto-thermoelectric responses, enabling the reading of nonvolatile memories storing information in the form of the magnetization direction. In antiferromagnets, a different group of magnets without a macroscopic magnetization, the moments cancel each other out by pointing in different directions. The discovery of antiferromagnets was thus delayed until 1949, after World War II, when neutron diffraction experiments became available [32]. Furthermore, despite there being far more antiferromagnets than ferromagnets, they have found limited applicational success due to their lack of magnetization, with one of the few examples being their use in memory materials to introduce an exchange bias.

However, antiferromagnets have been gaining increasing attention in the field of spintronics [9,10,11,12]. As mentioned earlier, antiferromagnets do not carry a magnetization and thus do not create a stray field. Therefore, antiferromagnets can be brought closer without interfering with each other, which is advantageous for miniaturization. In terms of reaction speeds, ferromagnets require a reversal of magnetic domains which can be considered a precession of the macroscopic spin. The speed of such a precession is known to depend on the anisotropy energy and is generally in the gigahertz range. In antiferromagnets, the energy cost of magnetization reversal is several orders of magnitude higher than that of ferromagnets, due to the exchange interaction between spins. Thus, the time scale of precessions reaches the order of terahertz, making antiferromagnets invaluable in the field of DX where high-speed information processing is critical. Therefore, extensive research is being actively conducted on the development of electrically recordable and readable nonvolatile memory using antiferromagnets.

Antiferromagnetic memory was first developed by Wadley et al. [33]. In 2016, they used a staggered spin-torque field to successfully change the spin direction by 90°, which they read using the anisotropic magnetoresistance effect. Subsequently, magnetic switching experiments have been performed on several antiferromagnets [34,35,36,37]. However, reading the spin direction using the anisotropic magnetoresistance effect requires the current and voltage reading directions to be at an angle of 45° to each other, limiting the future integration of antiferromagnets into devices. This specific geometry is incompatible with the four terminal Hall-measurement configuration used for ferromagnets, requiring eight terminals with reading and writing terminals arranged at 45° intervals.

Giant anomalous Hall effect in antiferromagnets

In our recent study, we conducted a principle demonstration of the world’s first four-terminal Hall-configuration memory device using an antiferromagnet [38]. The Hall device was created as a bilayer of an antiferromagnet and a heavy metal; the spin-orbit torque was employed for writing, and the Hall effect for reading the magnetization reversal. Here, we introduce Weyl antiferromagnets (Fig. 1a) that made such a device possible. This group of innovative magnetic materials shows many properties previously considered absent in antiferromagnets, such as the anomalous Hall effect, anomalous Nernst effect, and magneto-optical Kerr effect, due to the topology of the electronic structures [2,3,4,5,6,7, 20, 39]. The first known example of a Weyl antiferromagnet was the Mn₃X system developed by our group [2,3,4,5,6,7, 20, 39]. This system has a noncollinear antiferromagnetic order in which the magnetic moments of the Mn atoms on the Kagome lattice form a chiral 120° structure (Fig. 1b). The magnetic order can be controlled by a weak magnetic field of approximately 0.01 T despite Mn₃X being an antiferromagnet. Moreover, a large zero-field Hall effect close to the highest known value for ferromagnets is found at room temperature (Figs. 1c and 2a). The symmetry of the magnetic structure and the topology of the electronic bands are essential for the generation of this anomalous Hall effect. First, by considering a cluster of the six nearest neighboring moments, the 120° structure of the magnetic moment on Mn atoms can be viewed as forming a magnetic octupole (T_x^γ). These octupoles align ferromagnetically, breaking the macroscopic time-reversal symmetry (Fig. 1b) [4, 5, 40]. Second, it is observed that the electronic structure is topologically nontrivial near the Fermi energy due to the existence of a Weyl point, i.e., an intersection of linear dispersions. Thus, a large fictitious magnetic field (Berry curvature) exists in momentum space, leading to a large anomalous Hall effect and Nernst effect (Fig. 1a, b) [2, 6, 7].

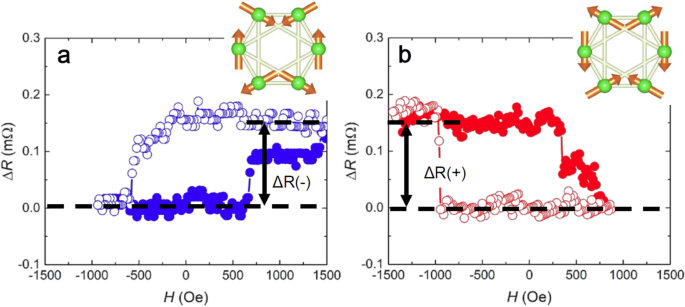
Furthermore, in collaboration with the Otani Group at the University of Tokyo Institute for Solid State Physics, our group has discovered a spin Hall effect in the Weyl antiferromagnet Mn₃Sn that is qualitatively different from the conventional spin Hall effect [41]. For the conventional spin Hall effect, the spin polarization is orthogonal to both the normal vector of the interface and the current, and this direction cannot be changed by a magnetic field. However, for the magnetic spin Hall effect observed in Mn₃Sn, the sign and direction of the spin polarization vector can be controlled by rotating the direction of the magnetic octupole of the Weyl antiferromagnet (Fig. 8), offering the potential for innovative new functionalities in spin conversion devices. It is theoretically proposed that the magnetic spin Hall effect may share its origins with the anomalous Hall effect, both being intrinsically caused by the fictitious magnetic field (Berry curvature). This once again indicates the significance of a topological electronic structure. An additional advantage over the conventional spin Hall effect is its efficiency in switching the perpendicular magnetization at zero field, as the spin accumulated at the surface can have a large perpendicular component.

Antiferromagnetic nonvolatile memory

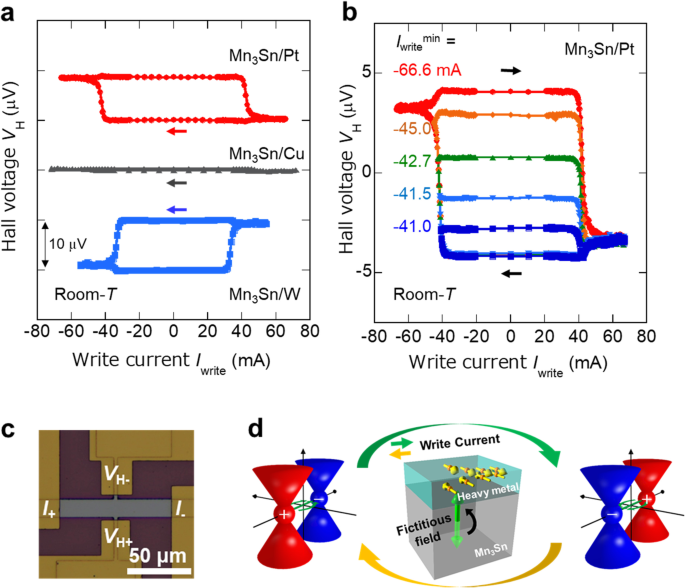
For the design of a nonvolatile memory using Weyl antiferromagnets, it is essential to develop a method to electrically control the giant responses produced by the topology of their electronic structure using electric current and/or spin current. We performed an experiment to verify whether the magnetic switching by a spin-orbit torque, used in ferromagnets, can be applied to the Weyl antiferromagnet Mn₃Sn [42, 43]. Specifically, a Hall-measurement device consisting of a multilayer film of Weyl antiferromagnet Mn₃Sn and nonmagnetic metals such as Pt, W, and Cu was fabricated on a silicon substrate [44], and the change in the Hall voltage for an external current was measured at room temperature [38].

The experimental results demonstrate that for the devices composed of Mn₃Sn and Pt or W, the sign of the Hall voltage generated by the Mn₃Sn layer can be reversed by applying a current of 10¹⁰ to 10¹¹ A/m² to the nonmagnetic metal layer (Fig. 9a, c, d). The cause of this Hall voltage reversal is concluded to be the spin current generated in the nonmagnetic metal layer, as shown in Fig. 9d, because (1) the Hall voltage reversal is caused by the external current in the devices using Pt and W; (2) the voltage reversal has opposite signs in the devices using Pt and W, corresponding to the difference in signs of their spin Hall angles [45, 46]; and (3) the reversal does not occur in the device using Cu, for which the spin Hall effect is negligibly small. Furthermore, in this device, the magnitude of the reversed Hall voltage can be controlled in an analog manner by changing the magnitude of the write current (Fig. 9b). This behavior as a memristor is known to originate from the polycrystalline nature of the Mn₃Sn film.

As explained earlier, the anomalous Hall effect in Mn₃Sn is derived from the giant fictitious magnetic field coming from the Weyl points in the vicinity of the Fermi surface (Fig. 1b). Essentially, the observed reversal of the anomalous Hall effect corresponds to the reversal of the pair of Weyl points with opposite magnetic charges in momentum space (Fig. 9d). The existence of Weyl fermions in our thin film of Mn₃Sn has been confirmed by carefully analyzing the transport properties, which are fully consistent with the expected chiral anomaly. This study is thus the first report on a successful electrical control of an antiferromagnetic Weyl semimetal state, or in other words, of its Weyl points [38].

These results demonstrate that control over Weyl points and other topological electronic structures is crucial to utilizing the giant anomalous Hall effect, anomalous Nernst effect, magneto-optical effect, and other large responses of antiferromagnets as nonvolatile memories. Furthermore, these inferences form the basis for the development of next-generation technology for ultrafast operation of an antiferromagnetic memory, as well as for the analysis of the current-induced propagation of magnetic domain walls and the associated magnetic dynamics in antiferromagnets.

The materials currently available are incapable of constructing an infrastructure that can fully support the rapidly proceeding DX. For example, to support the exponential growth in data transmissions with the current level of technology, data centers alone will require 10% of the total global energy. The development of quantum materials is indispensable in providing an ultimate solution to these problems.

This review summarizes the recent discoveries of topological magnets and the current status of their rapid development as the forefront of quantum materials. Topological magnets take advantage of their topological band structure and exhibit properties significantly enhanced from those of conventional magnets. The giant magneto-thermoelectric effect and the anomalous Hall effect in antiferromagnets are both examples of phenomena that have been realized in topological magnets. Although these breakthroughs are still in the nascent stages, having been discovered only a few years ago, they are expected to pave the way for the development of self-sustaining power supplies for IoT sensors, ultrafast and ultralow power consumption memory devices, and photoelectric interfaces in the coming ultrasmart society.